Некоторые обобщения метода моментов при оценивании плотности вероятности в виде ортогонального ряда
Автор: Браништи В.В.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 3 т.16, 2015 года.
Бесплатный доступ
Рассматривается задача оценивания функции плотности вероятности непрерывной случайной величины. Обсуждается актуальность данной задачи для науки и техники, в том числе для аэрокосмической отрасли. Рассматривается построение оценки функции плотности вероятности в виде ряда ортонормированных функций. Исследуется применение метода моментов для статистического оценивания коэффициентов ряда, а также предлагается его обобщение. В рамках применения метода моментов используются последовательные начальные моменты случайной величины. В этом случае расчёт оценок коэффициентов ряда сводится к решению системы линейных уравнений. Приводится доказательство теоремы о том, что при определённых условиях выбора ортонормированной системы функций предлагаемое обобщение метода моментов включает, как частные случаи, классический метод моментов, а также более распространённый метод оценивания коэффициентов в виде выборочных средних от ортонормированных функций. Показано, что при использовании ортонормированной системы Лежандра рассмотренные методы тождественны. Исследованы свойства построенных оценок, найдены их математические ожидания и ковариационная матрица. Показано, что в некоторых случаях оценки коэффициентов ряда являются смещёнными. Рассчитанные предложенным подходом оценки коэффициентов ряда были использованы для построения оценки функции плотности вероятности. Приводятся результаты численных расчётов значения функционала качества для построенных оценок функции плотности вероятности. Расчёты выполнены для случайной величины, подчинённой равномерному закону распределения. Произведено сравнение с известным методом оценивания коэффициентов при использовании чебышёвской и тригонометрической ортонормированных систем. Показано, что на малых выборках обобщённый метод моментов даёт существенно лучший результат.
Непараметрическая неопределённость, функция плотности вероятности, статистическое оценивание, ортогональные функции, метод моментов, матричный анализ
Короткий адрес: https://sciup.org/148177454
IDR: 148177454 | УДК: 519.2
Текст научной статьи Некоторые обобщения метода моментов при оценивании плотности вероятности в виде ортогонального ряда
Введение. Задача оценивания неизвестной функции плотности вероятности уже долгое время является важной научно-технической задачей [1]. От качества получаемых оценок плотности вероятности зависит качество основанных на ней алгоритмов классификации, распознавания образов, восстановления зависимостей и др. Кроме того, различные подходы к оцениванию плотности вероятности применяются при решении задач диагностики, часто встречающихся в аэрокосмической технике. Классический подход к оцениванию состоит в том, что подбирается модельный закон, который наилучшим образом описывает данную выборочную совокупность [2]. Однако в этом случае качество оценок существенно ухудшается при сложной структуре закона распределения случайной величины, например, если функция плотности многоэкстремальна, разрывна и т. п.
При отсутствии априорной информации о виде закона распределения используются непараметрические оценки функции плотности вероятности. Наиболее распространены ядерные оценки, основанные на работах Розенблатта [3] и Парзена [4], а также оценки в виде ряда ортонормированных функций, называемые проекционными оценками [5]. В последнем случае предполагается, что истинная плотность fx ) принадлежит функциональному гильбертову пространству L 2 [6]. Предположим сверх этого, что значения исследуемой случайной величины ^ с вероятностью 1 заключены в некотором отрезке. Не умаляя общности, будем считать, что ^ е [ - 1;1].
Проекционная оценка плотности вероятности имеет вид fn (x) = aоФо(x) +... + aNФn(x), (1) где {фj}”=о - полная система ортонормированных функций пространства L2; aj - коэффициенты, оцениваемые по выборке случайной величины ^; N - параметр, характеризующий длину ряда ортонормирован-ных функций, также подлежащий настройке. Как показывают численные расчёты, как коэффициенты aj, так и параметр N существенно влияют на качество оценки (1).
Так как оптимальными коэффициентами для оценки (1) являются коэффициенты Фурье
+х aj = j фJ(x)f(x)dx = M{ф/У}, -X j = о, ...,N, (2) то часто оценки aj коэффициентов строятся в виде выборочных средних значений функций фj(x):
1 n aj = Ефj(x), J = 0, -’N, (3)
n i=1
где x 1 , ..., x n - независимая выборка случайной величины ^ [7]. В [8] показано, что при использовании оценок (3) существует конечное оптимальное значение параметра N .
Кроме рассмотренного подхода к построению оценок aj возможно применение метода моментов [9]. В настоящей работе используются начальные моменты случайной величины ^. Так, приравняем оценки начальных моментов, рассчитанные по выборке, к их теоретическим значениям, рассчитанным с использованием оценки fN (x) в качестве функции плотности вероятности:
+”
j f n ( x ) dx = 1,
-X
+X j xfN (x) dx = E x
+X1
J xNfN (x) dx =-E xN. Jn
(-X
Подставляя вместо оценки fN ( x ) её выражение (1), получим систему из ( N + 1) линейных уравнений с ( N + 1) неизвестными:
а о ( 1, ф о ) + a ( 1, ф ) + ... + a N ( 1, ф n ) = 1,
1 Л a о (x, фо) + a1 (x, ф1) +... + aN (x, ф n )=~E хь n i=1
1 nn M a о (x , фо ) + a1 ( x , ф1 ) + ... + aN ( x , ф N )= ~ E xi ’
+x где (xi, фj )= j xi фj (x) dx - скалярное произведение
-X в пространстве L2. Введя матричные обозначения
B = {( xi, ф j)} , a = (a о, ..., aN) T , v = (1, ..., vn ) T, систему (4) можно переписать в виде
Ba = v . (4а)
Эта система имеет единственное решение, если матрица B не вырождена [1о]. В работе теоретически показано, что если используется система многочленов Лежандра, ортонормированная на отрезке [-1; 1], то матрица B не вырождена при любых конечных N > о.
Численно проверено, что для системы Чебышёва [11] и тригонометрической системы [12] матрица B не вырождена по крайней мере при N < 40. Тогда решение системы (4а) может быть записано в виде
Теорема . Пусть система { . i }”0 удовлетворяет следующему условию:
a = B - 1 v .
lim ||bn1|| max
N ^ot I II Hot o < k < N
xk
- Z( xk , ф / ) ф i ( x ) i =0
= 0
Данное решение, полученное методом моментов, может быть использовано для построения оценки функции плотности вероятности в виде выражения (1).
Обобщение метода моментов. Данный подход допускает следующее обобщение. Возьмём произвольное целое N' > N и рассчитаем матрицу при x е (-1;1), (7)
где II ’ IL — матричная норма, индуцированная векторной l „ -нормой [13]. Тогда при неограниченном увеличении N и фиксированном N оценка (6) сходится по вероятности к оценке (3):
B N ={ ( x i , ф у ) } ^
( 1 , ф 0 ) ( 1, ф N ‘ )
J x N' , . 0 ) - ( x N' , Ф N ' ),
Vs > 0
lim P
N' ^ot
a Jn )
1 ”
— Z. j ( x)
n , =1
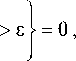
где 0 < j < N . (8)
размерности ( N ' + 1 ) х ( N ' +1 ) . Обратную к ней матрицу обозначим через B N 1 . Выделив в ней подматрицу BN N. , содержащую первые ( N + 1) её строк, и умножив её на вектор из ( N + 1) первых начальных выборочных моментов v , получим вектор
a ( N )
= в;
1N , N'
V ,
Доказательство. Докажем более сильное утверждение:
Vs> 0 N m P {I B N 1 » v .L>s ] = 0 (9)
где
■.-( 1 Z ф . ( x ), Z ф n ( x i ) 1■
I n i =1 n i =1 J
значения которого наряду со значениями (3) и (5) могут использоваться в качестве оценок коэффициентов для (1). Более того, справедлива следующая теорема.
Для этого заметим, что
I ■■ v.L=l B W- B .)L SI B N lLh- B .L
В свою очередь,
л
A r> ' V- Bn . v
n
1z xi n.=1
Ф
n
1 z xi
. n. =1
( ( 1, . 0 ) ( 1, Ф 1 ) — ( 1, ф N ) "
( x , . 0 ) ( x , Ф 1 ) — ( x N , Ф N' )
J x N , . 0 ) ( x N , . 1 ) — ( x N , Ф N ' )j
( 1 )
- Ё. 0( x i ) n i =1
1 n
- Z. 1( x i ) n i =1
1 n
1 Z . N ( x i )
I n i =1 J
( 1 4
- Zj -ZJ 1 , . j ) . j ( x i )
( N'
1 - Z ! 1, . j ) . j ( x)
j =0
n
1 Z x i n i =1 (
Z ( x , . j ) . j ( x i )
n
=1Z n i=1
N xi-Z(x,. j ).j( xi) j=0
n
1 Z xi n. =1 (
- Z( xN , . j ) . j ( x i )
x N -^E ( x N , »> , < x i )
I j =0 J
IIv - B N V .L
max
0< k < N'
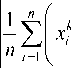
- Z( x k , . j ) . j ( x i ) j =0
< 1 Z max n 7 =1 0< k < N'
x i k
-
N
Z( x k , . j ) . j ( x) <
N'
< max max x k -V( x k ,.,).,( x, ) 1< i < n 0< k < n' i j =0V J) u
Тогда p|||bV -v II >sU P J||b^Hl max max
(II .Hot } III Hot 1< i < n 0< k < N 1
x k - Z( x k , . j ) . j ( x i ) >s> .
Возьмём теперь произвольное е > 0. В силу условия (7) с возрастанием N' выражение
S Ni max max
IIro 1< i < n 0< k < N'
N '
x k - Е( x k , ф j ) ф j ( x ) j =0
может быть сделано меньшим е, лишь только все x i е ( - 1;1). Однако для любой непрерывной случайной величины, распределённой на отрезке [ - 1;1],
Далее в статье предполагается, что система орто-нормированных функций выбрана таким образом, что условие (7) выполнено.
Свойства оценок. Найдём математические ожидания оценок (6):
M { a ( N ) } = M { В р л ‘ V } = В р л ‘ M { V } .
Так как
включение всех x i е ( - 1;1) выполнено с вероятностью 1. Таким образом,
T
|
lim P i n ^ro |
B at1 max max II IIro 1< i < n 0< k < N’ |
x i k |
- S ( x k , ф j ) ф/ x i j =0 |
< s |
.= 1 J |
|
или |
N |
||||
|
lim P J n ^ ro | |
B N 1 max max II IIro 1< i < n 0< k < N ’ |
x i k |
- Е( x k , ф j ) ф j ( x ) j =0 |
>s |
= 0. |
I n n n
= m - Ex0 , m -У x ,..., m - ExN ii i
I I nl =1 I nl =1 I nl =1
= V,
T
Теперь, переходя к пределу в неравенстве (10), получим формулу (9).
Неравенство Ц в р V - Vф || > s означает, что каждая компонента вектора B J V -Vф больше е. Отсюда следует, в частности, выполнение этого неравенства для первых ( N + 1) компонент. Таким образом,
то получаем окончательно
M { a ( N ‘) } = B n 1 n ‘ v .
При N ^ го получаем, что оценка является несмещённой:
lim M { a ( N ') } = M { a (ro) } =
N '^ro t ) ( )
U_ 1
1( 1 ”
=M11 -Ea( x), I I n i=1
...
1 .
,- ЕфN (x)
П i =1
lim P
N '^ro
a (N)
1 n
- Е ф j ( x i ) n i =1
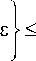
< lim P {I| B N 1 v-Vф|| >s } = 0, 0 < j < N . N ’ ^ro П™ )
= ( M Ш^)}, ..., M { ф N ( ; )} ) T = a .
При конечных N оценка (6), в общем случае, смещена.
Рассчитаем ковариационную матрицу оценок:
Теорема доказана.
Из доказанного следует, что при условии (7) рассматриваемое обобщение метода моментов включает метод (3) как частный случай при N ‘ ^ ro . Поэтому для оценок (3) вводится обозначение а (”) . С другой стороны, очевидно, что при N ‘ = N метод совпадает с обычным методом моментов. Для оценок функции плотности вероятности с коэффициентами (6) и (3) вводятся, соответственно, обозначения f N N ) ( x ) и f Г( x ).
Можно показать, что для систем Лежандра, Че-бышёва и тригонометрической системы выполняется условие (7). Причём для системы Лежандра выражение под пределом в (7) равно 0 при любом N > 0. Действительно, для системы Лежандра имеем kk xk = Е С,ф,( x) = Е( xk ’ ф i )ф-( x) при x е (-1;1), i=0 i=0
k = 0, 1, 2, ...;
s{ a(N ‘) } = s{ Bn1 n 'V
1 »-1
= BN , N'z
n
1 I T
где
X - ковариационная матрица степеней случай-
ной величины ^: ( 0
X =
Переходя к
D®
cov
II B ^1|| max x k
II IIго 0< k < N
N
- Е( x k , ф^фР x ) i =0
=1 I b n 'I L a x - x i=1 I b n 'I L -°=°.
Поэтому при использовании системы Лежандра оценки, полученные по обобщённому методу моментов при любом N , совпадают с оценками (3).
0 '
cov {;,; N'}
пределу при N ^
риационную матрицу оценок (6):
где х ф
.
го, получим кова
lim s { a ( N ') } =^ { a ( ro ) } = 1 X
N' ^ro I J I > n
- ф,
—
ковариационная матрица функций
{ ф 0( x ), ..., ф N ( x )} от случайной величины р
Х ф
( D { ф o } cov{ ф 1 , ф 0 }
cov{ ф N - , ф 0 }
COv{ ф o , ф 1 } — COv{ ф o , ф N - P D ^} — cov{ ф 1 , ф N }
cov{ ф N, , ф 1} — D { ф N, }
.
Отсюда видно, что при неограниченном увеличении объёма выборки n дисперсии оценок стремятся
к 0. Тогда из теоремы Чебышёва [9] оценки a (”) являются состоятельными.
Применение оценок. Несмотря на отсутствие при конечных N для оценок a ( N ) таких свойств, как несмещённость и состоятельность, в некоторых случаях, особенно на малых выборках, оценка плотности вероятности f NN ) ( x ) всё же оказывается лучше, чем оценка f N^ ( x ). Близость оценки f N ) ( x ) к истинной плотности f ( x ) характеризуется усреднённым квадратичным критерием [14]:
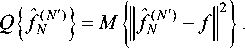
После преобразований получаем следующее выражение [8]:
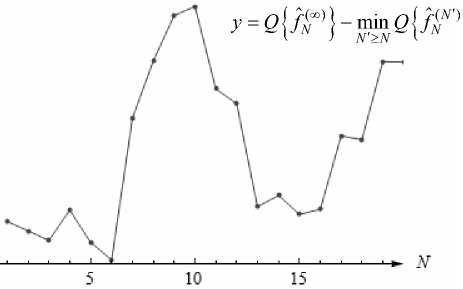
Q {fN) } = | f - fA |2 +
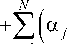
j =0
- M
.7 N
{aN }) +2 D {aГ'}, j=0
где fN ( x ) - оценка плотности вероятности с оптимальными коэффициентами:
f N ( x ) =а 0 Ф 0( x ) + ... + а N Ф N ( x )- (12)
Выражение (11) позволяет значительно ускорить процесс вычисления значения критерия Q для данной ортонормированной системы {ф i } и данной плотности вероятности f ( x ).
Обобщённый метод моментов был применён при восстановлении различных законов распределения вероятностей. Графики зависимости разности между значением критерия (11) для оценки f N^ ( x ) и оценки f NN ) ( x ) при оптимальном N представлены на рис. 1 и 2. Рассматривалась задача восстановления равномерного закона распределения на отрезке [0; 0,5]. Результаты получены при малом объёме выборки n = 20.
Из графиков видно, что на малых объёмах выборки обобщённый метод моментов при оптимально настроенных конечных N в широком диапазоне значений N даёт существенное улучшение качества оценки функции плотности вероятности.
0.0015
0.0010
0.0005
0.0000
}
Рис 1. Сравнение качества аппроксимации при восстановлении плотности вероятности методами (3) и (6) с использованием ортонормированной системы Чебышёва
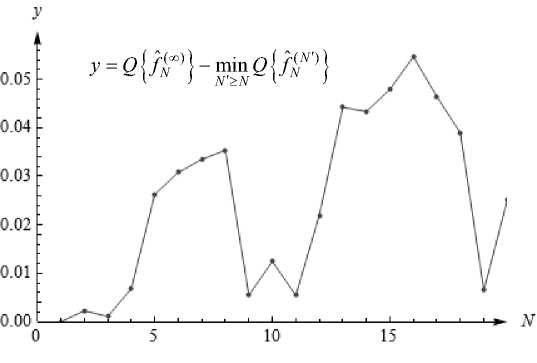
Рис 2. Сравнение качества аппроксимации при восстановлении плотности вероятности методами (3) и (6) с использованием ортонормированной тригонометрической системы
Заключение. В ходе исследования было разработано обобщение метода моментов для оценивания коэффициентов проекционной оценки (1) функции плотности вероятности, для которого методы оценивания (3) и (5) являются частными случаями. В некоторых случаях, особенно при малых объёмах выборки исследуемой случайной величины, удалось добиться улучшения оценки плотности вероятности по сравнению с наиболее часто используемым методом (3), несмотря на отсутствие у оценок коэффициентов таких свойств, как несмещённость и состоятельность. Здесь уместно замечание известного советского математика В. Н. Вапника: «Ниоткуда не следует, что в классе несмещённых оценок плотности имеются достаточно хорошие оценки. Ведь, как уже отмечалось, само свойство несмещенности оценки не имеет никакой самостоятельной ценности и вводится исключительно в целях ограничения класса оценок» [15].
Список литературы Некоторые обобщения метода моментов при оценивании плотности вероятности в виде ортогонального ряда
- Акимов С. С. Методы решения задачи восстановления плотности вероятности по выборке из генеральной совокупности//Естественные и математические науки в современном мире. 2014. № 1 (13). С. 29-35.
- Кобзарь А. И. Прикладная математическая статистика: для инженеров и научных работников. М.: Физматлит, 2006. 816 с.
- Rosenblatt M. Remarks on some nonparametric estimates of a density function//The Annals of Mathematical Statistics. 1956. Vol. 27, № 3. P. 832-837.
- Parzen E. On estimation of a probability density function and mode//The Annals of Mathematical Statistics. 1962. Vol. 35, № 3. Pp. 1065-1076.
- Ченцов Н. Н. Статистические решающие правила и оптимальные выводы. М.: Физматлит, 1972. 520 с.
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. 6-е изд., испр. М.: Наука, 1989. 624 с.
- Ченцов Н. Н. Оценка неизвестной плотности распределения по наблюдениям//ДАН СССР. 1962. Т. 147, № 1. С. 45-48.
- Новосёлов А. А. Об оптимальном выборе структуры функции плотности вероятности и регрессии: препринт. Красноярск: ВЦ СО АН СССР, 1979. 31 с.
- Крамер Г. Математические методы статистики: пер. с англ. 2-е изд., стер. М.: Мир, 1975. 648 с.
- Мальцев А. И. Основы линейной алгебры. 3-е изд. М.: Наука, 1970. 400 с.
- Никифоров А. Ф., Уваров В. Б. Специальные функции математической физики. 2-е изд., перераб. и доп. М.: Наука, 1984. 344 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. 8-е изд. М.: Физматлит, 2003. Т. 3. 728 с.
- Хорн Р., Джонсон Ч. Матричный анализ: пер. с англ. М.: Мир, 1989. 655 с.
- Епанечников В. А. Непараметрическая оценка многомерной плотности вероятности//Теория вероятностей и её применения. 1969. Т. 14, № 1. С. 156-162.
- Вапник В. Н. Восстановление зависимостей по эмпирическим данным. М.: Наука, 1979. 448 с.
- Akimov S. S. . Estestvennye i matematicheskie nauki v sovremennom mire. 2014, Vol. 1 (13), P. 29-35 (In Russ.).
- Kobzar A. I. Prikladnaya matematicheskaya statistika: dlya inzhenerov i nauchnykh rabotnikov . Moscow, Fizmatlit Publ., 2006, 816 p.
- Rosenblatt M. . The Annals of Mathematical Statistics, 1956, Vol. 27, 3, P. 832-837.
- Parzen E. On estimation of a probability density function and mode. The Annals of Mathematical Statistics, 1962, Vol. 35, No. 3, P. 1065-1076.
- Chentsov N. N. Statisticheskie reshayushchie pravila i optimal’nye vyvody . Moscow, Fizmatlit Publ., 1972, 520 p.
- Kolmogorov A. N., Fomin S. V. Elementy teorii funktsiy i funktsional'nogo analiza . 6th edition. Moscow, Nauka Publ., 1989, 624 p.
- Chentsov N. N. . Doklady Akademii nauk SSSR, 1962, Vol. 147, No. 1, P. 45-48 (In Russ.).
- Novoselov A. A. Ob optimal’nom vybore struktury funktsii plotnosti veroyatnosti i regressii: preprint . Krasnoyarsk, Computational Centre of Siberian Department Academy of Science USSR Publ., 1979, 31 p.
- Cramér H. Mathematical methods of statistics. Princeton University Press, 1946, 575 p.
- Maltsev A. I. Osnovy lineynoy algebry , 3rd ed. Moscow, Nauka Publ., 1970, 400 p.
- Nikiforov A. F., Uvarov V. B. Spetsial’nye funktsii matematicheskoy fiziki , 2nd ed. Moscow, Nauka Publ., 1984, 344 p.
- Fikhtengol’ts G. M. Kurs differentsial’nogo i integral'nogo ischisleniya . 8th ed. Moscow, Fizmatlit Bubl., 2003, Vol. 3, 728 p.
- Horn R., Johnson C. Matrix analysis. Cambridge University Press, 1990, 561p.
- Epanechnikov V. A. . Teoriya veroyatnostey i ee prilozheniya, 1969, Vol. 14, No. 1,
- P. 156-162 (In Russ.).
- Vapnik V. N. Vosstanovleniye zavisimostey po empiricheskim dannym . Moscow, Nauka Publ., 1979, 448 p.


