Некоторые особенности численного решения задач термоупругости и гидродинамики теплопроводящей сжимаемой вязкой жидкости с помощью универсальных пакетов

Численное моделирование физических процессов, описываемых дифференциальными уравнениями в частных производных, приобрело в последнее время "эпидемический" характер, что можно объяснить остро назревшей необходимостью решения насущных прикладных задач, не решаемых или очень непросто решаемых аналитическими или асимптотическими методами. К настоящему времени разработано большое количество универсальных пакетов на основе метода конечных элементов, позволяющих решать широкий класс задач механики сплошных сред: гидродинамики, газодинамики, деформируемого твердого тела и т. п. В качестве примеров таких пакетов можно назвать "ANSYS", "NASTRAN", "COMSOL", "ASKA", "ADINA" и др.

Особенно актуальным такое моделирование становится при решении т. н. связанных задач, когда в реальном физическом процессе присутствуют различные поля, взаимодействующие друг с другом (решение таких задач в аналитическом виде, за исключением некоторых частных случаев, весьма проблематично). В качестве таких процессов можно упомянуть связанные задачи термоупругости, задачи гидродинамики при учете уравнений тепло-переноса и т. п. Упомянутые пакеты, как правило, предусматривают возможность решения таких мультифизичных задач. При этом от пользователя требуется высокая квалификация для грамотного выполнения всей работы, начиная с выбора корректной математической модели и постановки краевых и начальных условий и заканчивая адекватной интерпретацией конечных результатов.

В настоящей работе на примере решения связанных задач термоупругости и системы уравнений Навье—Стокса для вязкой сжимаемой теплопроводящей жидкости показаны особенности работы пакета "COMSOL Multyphysics".

СИСТЕМА УРАВНЕНИЙ НАВЬЕ—СТОКСА. СЛУЧАЙ ТЕПЛОПРОВОДЯЩЕЙ, ВЯЗКОЙ, СЖИМАЕМОЙ ЖИДКОСТИ

Разбор алгоритмов решения системы уравнений Навье—Стокса начнем с уравнения теплопе-реноса. В [1] приведена следующая модель тепло-переноса в жидкости

pc | — + v -V T ^p Vett

-V - q + ст ': S -

-

p

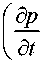
Здесь ρ , c_p — плотность и удельная теплоемкость

жидкости при постоянном давлении; q — плотность

потока тепла; σ ' — вязкий тензор напряжений;

S — тензор скорости деформации;

S = 1 ( V v + ( V v ) ^T ) (значок T

в верхнем индексе

означает транспонирование, и его не надо путать с абсолютной температурой); v , p — скорость и давление в жидкости; T — абсолютная температура, T = T 0 + 9 , где T 0 — равновесная температура, θ — переменная ее часть, для которой справедливо условие 9 / T 0 ^ 1. Наконец с ': S означает скалярное

произведение двух тензоров, σ ': S = ZZc ij

Обозначим 0 = V • v , X и ц — параметры Ламе жидкости.

Здесь уместно отметить, что в литературе по гидродинамике, и иностранной (см., в частности работу [2], которая представляет в знаменитой физической энциклопедии "Handbuch der Physik", т. VIII/I, механику жидкости), и отечественной (см. классическую монографию [3]), приняты следующие нотации вязкого тензора напряжений в однородной изотропной среде. В векторной и координатной записи выражение для вязкого тензора напряжений либо имеет вид [2, с. 204]

о ' = 2 ц S + X 0 I ,

,       ( д v   д v, 1 , е д v, с = ц ц —L + —- + X5ik —l-, ikik

(дxk   axi)a либо [3, с. 72]

о ' = 2 n S + 1 Z - 2 П j® I ,

,     ( д v  д vk  2   д v 1

^с ,k = П — ⁺ -А, I ^{+ qS}. - ^.

(дхк   дx   3   дxl )д

Здесь I — единичный тензор; η и ς — сдвиговая и объемная (вторая) вязкость. Как будет показано ниже, тензор вязких напряжений в [1] принят несколько в иной форме.

В (1) член

—

p определяет работу давления, а член σ :S

нагрев, вызванный наличием вязкости [1].

Учитывая закон Фурье q = —KV T

( κ — коэффициент теплопроводности), малую величину члена (2) при малых числах Маха, а также малость члена (3), выражение (1) переписывают в "облегченном" виде [1]

p c p ^ + p c p ( v •V T ) = V^ ( k V T ) .

При к = const имеем

P c p ^ I ⁺ P c p ( ^v '^VT ) = k ^ ^T .

(1а)

На допустимости таких упрощений остановимся ниже.

Следующие уравнения системы Навье—Стокса: собственно уравнение Навье—Стокса и уравнение неразрывности — представлены в [1] в следующем виде

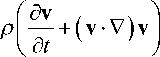
(                 xT 2                I

= —V p + V^I ц ( V v + V v ) — — p(V^ v ) I I ,

( P v ) = 0.

5P + v д t

Последнее выражение (уравнение неразрывности) общеизвестно и в комментариях не нуждается. Не так с уравнением (5). Отметим, что наличие в (5) только коэффициента сдвиговой вязкости µ отнюдь не говорит о том, что уравнение (5) описывает движение несжимаемой жидкости.

Уравнение Навье—Стокса для сжимаемой жидкости при постоянных коэффициентах вязкости описывают обычно либо в терминах коэффициентов динамической вязкости (параметров Ламе) λ и µ [2, с. 206]

(дv pl — + (v• V)v I = —Vp + ^\v + (X + ц)VV• v, (6)

либо в терминах коэффициентов η и ς [3, с. 73]

(дv               1( pl — + (v •V) v =—Vp + nAv+ ^ + — VV • v. (7)

(д t V 1                    (

Между параметрами Ламе, с одной стороны, и сдвиговой и объемной вязкостью, с другой стороны, как видно из сравнения (6) и (7), имеет место соотношение

П = ц , q = X + 3 ц .

Известно [3, с. 73, 274], что n >  0 и q >  0 .

Выражения (6) и (7) с учетом соотношений (8) тождественны. Выражение (6) может быть записано в виде (см. [2, (61.1), с. 204 и (61.4), с. 206])

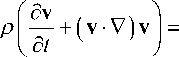
= —V p + V- ( ц ( V v + V v ) T + X ( V^ v ) I ) .    (9)

Сравнение выражений (5) и (9) показывает, что они совпадают при условии

3 X + 2 ц = 0.

Если перейти в (10) к параметрам η и ς , используя (8),

31 + 2ц — з(Z -2п) + 2n = 3Z , то получим

3 Z = 0,     или Z = 0.         (10а)

Выражение (10) представляет собой соотношение Стокса между коэффициентами вязкости жидкости [2, с. 208]. Здесь приведем цитату из этой работы о пределах справедливости соотношения Стокса (10): "…можно утверждать следующее: для одноатомных газов (соотношение) выполняется с достаточной степенью точности; с другой стороны, для жидкостей и многоатомных газов коэффициент 1 >  0 может иногда во много раз превосходить коэффициент µ ".

Выражение (10а) показывает, что соотношение Стокса (10) равносильно равенству нулю второй (объемной) вязкости ζ , что для обычных жидкостей далеко от реальности (см., например, статью "Объемная вязкость" в Физической энциклопедии. Т. 3. М.: БРЭ, 1992. 395 с.). В соответствии с этим фактом необходимо контролировать реальные значения параметров λ и µ на предмет их соответствия соотношению Стокса (10), либо решать корректные уравнения (6) или (7).

Отметим, что в работе [4, с. 23] сказано следующее (перевод авторов): "вторая вязкость ς существенна только для сжимаемых жидкостей (акустика), а для многих простых жидкостей предположение Стокса

4 q « 3п является хорошим приближением".

Здесь необходимо уточнить, что последнее соотношение совпадает с соотношением Стокса (10а) только при условии п — 0. Отметим, что выраже-4

ние q — —п , действительно, эквивалентно соотношению (10) 3 1 + 2 ц — 0 при q — п — 0 , что следует из (8) и является банальным.

Как видно из выражения (7), при выполнении равенства (10а) это уравнение тождественно совпадает с уравнением (5). Отметим, однако, что равенство нулю объемной вязкости отнюдь не говорит о несжимаемости жидкости, которая и в (5), и в (7), и в (6), и в (9) при этом подразумевается сжимаемой в силу отличия от нуля дивергенции скорости в последних членах справа в этих уравнениях.

Таким образом, уравнение (5) описывает динамику вязкой сжимаемой жидкости при равной ну- лю объемной вязкости, что в общем случае не соответствует действительности.

Замечание 1. В пакете существует возможность создавать пользовательские уравнения, поэтому, вероятно, можно модифицировать уравнение Навье— Стокса (5) к виду (6) или (7).

Остановимся на версии (1) уравнения теплопе-реноса. В отечественной литературе принята следующая координатная нотация уравнения теплопе-реноса в вязких сжимаемых жидкостях [3, с. 272]:

— + v -V s | — о \к ^v- + V-(kV T). dt          ) ik dxk

Перепишем его в векторном виде:

Ssi

— + v -V s — a ': S -V- q .

dt)

Воспользуемся далее известным термодинамическим соотношением (см., например, [5], [6])

d s — — d T - — d p . T ρ

Здесь s — энтропия единицы массы жидкости; c_p — удельная теплоемкость жидкости при постоянном давлении; α — изобарный коэффициент расширения (коэффициент температурного расширения)

1 Г ⁵ V ) _ 1 Г^бР ) v (a T) _p p (a t ) p

где V — удельный объем. Из (12) получаем выражения

V s — cp- V T - a Vp , Tρ

d s c p a T   a d p

— —-----.

at   t at   p at

после подстановки которых в (11) получаем

ρ T

Г c p 5 T ₍ t a t

a ap ---— + v - p St

— a ': S -V- q

или окончательно:

Г a t         i     Г ap     „i„ pc„ — + v- VT — Ta — + v-Vp -V-q + a':S .

^p la t        )     (a t )

Подставляя в последнее выражение значение α из (11), получаем

ρ c_p

— + v-V T d t

—

I (Sp + ( v -V ) p ]. T a Sp .

¹ _p (d t ^v ’ J       a t

т (Sp Л (Sp

= -V- q + CT ': S I II — + v -V p | ,     (14)

p (a t J_p (a t       J

что в точности совпадает по форме с выражением (1), принятом в пакете.

Замечание 2. Несмотря на кажущееся совпадение уравнений теплопереноса в жидкости (1) в пакете и общепринятого (14) (см. [2, 3]), между ними имеется существенное различие, заключающееся в различиях тензоров вязких напряжений в том и в другом случаях. Стандартный тензор вязких напряжений приведен выше и равен ct ' = 2 p S + Л 0 1 , а соответствующий тензор, фигурирующий в пакете, можно определить из пакетной версии уравнения Навье—Стокса (5):

ст ' = p ( V v + V v ) ^T

^- 3 p (^{V- v} ) I .

Далее остановимся на вопросе правомерности отбрасывания членов (2) и (3) в выражении (1) при переходе к выражению (1а).

Рассмотрим член (2), отвечающий за работу

Отсюда видно, что работа давления пренебрежимо мала только в случае малых α и / или ма-dp о лых производных давления . Во всех осталь ных случаях нет оснований пренебрегать этим членом по сравнению, например, с членом v - V T в (1), который в общем случае является величиной второго порядка малости при малых числах Маха.

Анализ члена (3) σ ': S показывает, что он имеет величину второго порядка малости и при малых числах Маха сравним с членом v - V T справа в (1).

Отметим, что в [1] предусмотрена возможность учета в (1) обоих слагаемых (2) и (3) и вместе, и по отдельности. При добавлении члена σ ': S , названного в пакете Viscous heating Term, необходимо учитывать Замечание 1.

Замечание 3. Для работы с несжимаемой жидкостью необходимо просто принять V - v = 0 в уравнении Навье—Стокса (5), которое принимает в этом случае вид

давления,

—

p

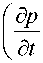
( dv               I                                   xt\ pl— + (v-V) v I = —Vp + V-(p(Vv + Vv) ).

Величина

T (d p I p (a t ^J

согласно (13), равна

—

T I d p I _T

—I — I = T a .

P (d T J p

Величина

, согласно [2, с. 15], рав-

на

Ia p , I d p — + ( v -V ) p = —,

Vet ^{v     7} J dz

Таким образом, математическая модель системы уравнений Навье—Стокса для вязкой теплопроводящей сжимаемой жидкости в пакете принята с некоторыми натяжками. А именно, при использовании уравнения Навье—Стокса (движения) (5) необходимо внимательно следить за справедливостью выполнения соотношения Стокса (10). При использовании уравнения теплопереноса (1) необходимо контролировать правомерность пренебрежения членами (2) и (3), по необходимости используя в (3) корректный вязкий тензор напряжения ст ' = 2 p S + Л 0 1 .

Отметим, что система уравнений Навье—Стокса представляет собой систему связанных уравнений, в которые входят все искомые поля.

где p — полная производная давления по вре-dt мени. Окончательно имеем

ТЕРМОУПРУГОСТЬ

—

I (Sp + ( v -V ) p I = T a dp .

¹ p (d t ^{V 7} J        d t

Анализ члена (v -V)p говорит о том, что он имеет второй порядок малости по сравнению со ap                       .,     _ слагаемым при малых числах Маха. Таким a t образом, можно приближенно написать

Уравнение теплопроводности в твердых телах с учетом влияния деформации на температуру при не зависящих от температуры и пространственных координат коэффициентах в работах [8, 9] выглядит следующим образом:

c_F — + K a T V--- к A T = 0.     (15)

^£ a t                a t      ¹

Здесь введены обозначения, соответствующие [8, 9] (которые будут далее фигурировать и в линейном

уравнении упругости): T — абсолютная температура тела; u — вектор смещения; c _ε — удельная теплоемкость при постоянной деформации; K = Я 1 + y p _J — объемный модуль упругости; α — коэффициент термического расширения тела (11); λ ₁ , µ ₁ — упругие модули Ламе для тела; ρ ₁ — его плотность; κ ₁ — коэффициент теплопроводности тела.

В работе [10, с. 174] получено уравнение, совпадающее с (15), в котором вместо удельной теплоемкости при постоянной деформации c _ε фигурирует совпадающая с ней теплоемкость при постоянном объеме c_V . Перепишем поэтому (15) в более привычном виде:

cv — + KaT V — - к AT = 0.(15а)

V dtd

(В работе [10] допущена описка: вместо верного Kα2T соотношения cp - cV =------, следующего из со- p отношений [11, с. 70, (16. 9), (16. 10)], фигурирует соотношение cp - cV = Ka2T0; T0 — равновесная температура).

Уравнение теплопроводности в [1] для движущихся твердых тел при постоянном коэффициенте теплопроводности κ1 имеет вид dT„

Pj cp^;+Pj cp v ’V T - kja T =0, d t или после деления на κ1

ρc

' d + rUL v .V T-A T = 0.(16)

к ₁ d t      k _j

Здесь ρ1 , cp — соответственно его плотность и удельная теплоемкость при постоянном давлении; v — вектор скорости поступательного движения (translational motion) твердого тела как целого; Kj = xJ — коэффициент температуропро-ρ1cp водности тела. Практически такое же уравнение для движущегося тела получено в работе [7, с. 21].

При условии равенства нулю скорости поступательного движения тела v = 0 уравнение (J6) упрощается до обычного уравнения теплопроводности [1]

d T

P j cp — ^{- k} j ^{A T} = ⁰.

d t

Как видно, в уравнении (16) не учитывается влияние механической деформации на температуру. В пакете предусмотрен учет такого влияния добавкой опции "Pressure Work", которая равна [12]

T^se- = Ta—(°, + °22 + °33), dt         d tv 22 v где sel — эластичная добавка к энтропии, равная в изотропном случае sei = a (°JJ + °22 + ° 33 ) .

После чего уравнение теплопроводности приобретает в [12] вид dd _ d pc — + Ta—° - к A T = 0,   (J7)

J p dt         dt         J где, как обычно, по повторяющемуся индексу ведется суммирование

°ll = ° П ⁺ ° 22 ⁺ ° 33 .

В (J7) во втором слагаемом принимаем T = T ₀ вследствие допущения T - T₀ ^ T .

Согласно [8, с. 14] имеет место равенство

° ii = ^{3 K} ( ^{e - a9} ) .

Здесь e = divu ; 9 = T - T0. Подставляя все величины в (17), получаем dT          du      2T dT        n pc„ — + 3KaTV---3Ka Tn--к AT = 0.

^{J p} d t            ⁰      d t             ⁰ d t      ^J

99 dT „

Здесь учтено, что — = —. Далее для упроще-д t    д t ния последнего уравнения воспользуемся приве-

Kα2T денным выше тождеством c - cV =-----, или p cppj = pjcV + Ka2T0. Тогда последнее уравнение запишется в виде

,            . x d Td

(pjcjV + Ka T0)— + 3KaT0V- — -v                  ' dt

• - 3 Ka² T--к A T = 0,

• 0 d t

или

( p _J c_V - 2 K a ²T₀ ^^T- + 3 K a T₀ V • | u - k _j A T = 0. (J8)

Как видно, (18) совпадает с (15), (15а) по структуре, но отличается коэффициентами. При этом они не приводятся друг к другу принципиально, т. к. не могут быть получены друг из друга умножением одного из уравнений на функцию или константу (вектора коэффициентов двух уравнений линейно независимы: при вторых членах они отличаются втрое, а при третьих — равны).

Определяющее уравнение в изотропной, однородной среде, связывающее тензор напряжения σ с тензором деформации ε и возмущением температуры 9 = T - T 0 при условии малости деформации и отношения θ / T ₀ , где T ₀ — равновесное значение температуры тела, имеет вид (закон Дюамеля—Неймана) [8, с. 14]

а = 2 p 1 £ + ( A 1 V- u + K a9 ) I . (19)

Линейное уравнение движения, соответствующее (19), имеет вид [8 с. 22]

d ² u

P = p A u + ( ^ + p ) VV ■ u - Ka V 9 . (20) ¹ у t 2.1 ¹ 1,

В пакете [12] определяющее уравнение носит название закона Дюамеля—Гука и применительно к нашему случаю имеет вид а = C: (£ - a91). (21)

Здесь C — тензор упругости, и в изотропном однородном случае представляет собой симметричную квадратную разреженную матрицу, все отличные от нуля элементы которой суть только постоянные величины p 1 , Х 1 или Л 1 + 2 p 1 .

Отметим, что выражение (19) также получено из выражения типа (21) (см. выражение (11) работы [8, с. 13]) с помощью упрощения тензора упругости C для случая однородного изотропного материала. Отсюда следует, что определяющее уравнение (21) должно совпадать с определяющим уравнением (19) в случае изотропного однородного материала.

Таким образом, при реализации термоупругой модели твердого тела существуют отклонения уравнения теплопроводности от классического вида, хотя по структуре выражения близки.

ВЫВОДЫ

Проделанный выборочный анализ адекватности конкретного пакета по численному решению задач математической физики показал необходимость обязательной верификации алгоритмов, принятых в пакете. После этого необходимо либо следовать пакету, либо прописывать в пакете собственные математические модели.