Некоторые особенности моделирования микрофлюидных процессов

При расчете микрофлюидных процессов, описываемых, в частности, уравнением Навье— Стокса, возникают некоторые трудности вычислительного характера, связанные с выбором сетки метода конечных элементов из-за малого отношения радиуса капилляра к его длине. Эти сложности могут быть ослаблены с помощью теории подобия [1], сводящей изучение исходной модели к изучению подобной модели, в которой эти трудности отсутствуют. В случае моделирования течений вязких жидкостей наиболее известно использование уравнения Навье—Стокса для несжимаемой жидкости по той причине, что в этом случае можно обойтись единственным критерием подобия, равным безразмерному числу Рейнольдса Re [1, 2].

ПОСТАНОВКА ЗАДАЧИ

Целью работы является замена исходной модели подобной ей моделью, позволяющей обойти трудности численного решения задачи. Для этого необходимо привести ограничения, при которых можно свести исходное общее уравнение Навье—Стокса к уравнению для несжимаемой вязкой жидкости, а далее воспользоваться простейшим случаем подобного моделирования при наличии только одного критерия подобия — числа Рейнольдса и остановиться на технике для соответствующего моделирования с целью проектирования приемлемой модели.

РЕШЕНИЕ ПРОБЛЕМЫ

Рассмотрим уравнение Навье—Стокса для сжимаемой жидкости [2, 3]

I 0V                 1                        I П 1р — + (v -V) v = -Vp + nAv + q + — VV • v . (1)Id/         ’ )                  I 3 J

Здесь ρ , p , v , — плотность, давление и вектор скорости в жидкости; η и ς — сдвиговая и объемная (вторая) вязкость. Как известно [2], при некоторых условиях на переменные течения жидкость можно считать несжимаемой, что математически эквивалентно условию V • v = 0 . Тогда (1) преобразуется к уравнению Навье—Стокса для несжимаемой жидкости

I dv             1p I — + (v • V) v I = -Vp + nAv.

Далее приведем условия, при выполнении которых жидкость можно считать несжимаемой, что формально означает выполнение неравенства

A p   ,

— << 1, ρ где Ap — вариации изменения плотности жидкости. Сошлемся на работу [2]. При стационарном движении достаточным условием выполнения предыдущего неравенства является [2, с. 41] малое отношение амплитуды скорости движения жидкости v к скорости звука c (малость числа Маха M )

| v| <<  c , или M <<  1.

При нестационарном движении необходимо выполнение еще одного условия [2, с. 41–42]. Пусть τ и l — величины порядка промежутков времени и расстояний, на которых скорость жидкости испытывает заметное изменение (при периодическом процессе за τ принимается период).

Тогда это условие имеет вид l т >> —.

c

Наконец, при учете теплопроводности жидкости, для того чтобы можно было считать плотность постоянной, необходимо помимо выписанных условий, чтобы имеющиеся в жидкости абсолютные перепады температур были достаточно малы [2, с. 277].

Следуя [4, с. 25, 26], приведем (2) к безразмерному виду. Для этого принимаются следующие преобразования всех функций, входящих в (2), таким образом, чтобы они стали произведением размерных множителей на безразмерные переменные. Начнем с координат и вектора скорости:

r = ( x , y , z ) = L 0 r = L 0 • ( x , y , z ) ,            ⁽³⁾

V = V o v .                                   (4)

Здесь коэффициенты L ₀ и V ₀ имеют соответствующие размерности

[ ^L 0 ] = м,     [ V o ] = м/с.

Введенные масштабы длины L0 и скорости V0 фиксируют шкалы времени и давления. Для времени выбор масштабного множителя очевиден t = -°t = 70t,        [ To ] = с.       (5)

V ₀

Для давления несколько сложнее. В [4] отмечается, что через параметры задачи размерность давления выражается двояко: либо так

ρ

Г V, dv I To d "t

+ — (v -v) v

L 0

- PL vp + nV V 2v.

² L ₀        L ₀

Естественно, в (8) все коэффициенты при безразмерных переменных имеют одинаковую размерность. После деления обеих частей (8) на величину

PL = nVo L0    L02 , получается безразмерное уравнение [4, с. 26]

Re

'dv

(d "t

v - V ) v

= -V p + V v .

Здесь безразмерное число Рейнольдса Re опреде-

ляется так:

p =     p = P o p ,    [ P o ] =      = Па = "Н , ⁽⁶⁾

Lo                   L L o J       м либо так p = PVo2 p = Po p ,   [Po ] = [PVo2 ] = Па = -Н- (7)

м ²

Re = ^{p L 0} V L .              (10)

η

Замечание. При принятии равенства (7), т. е. P_o = PV ₀ 2 уравнение (9) преобразуется к уравнению [5, с. 272]

+ ( v -V ) v = -V p + —V v .    (9а)

5 t ^x ’           Re

Из сравнения (9) и (9а) видно, что при малых числах Рейнольдса действительно нужно пренебрегать инерционным, а при больших числах Рейнольдса — вязким членом уравнения.

Ценность уравнений (9), (9а) для моделирования соответствующих течений трудно переоценить. Пусть рассматриваются две модели с соответствующими преобразованиями (3)–(6) для каждой из них и характеризующими числами Рейнольдса Re1 и Re2 . Тогда каждый процесс опишется соответственно уравнением

Re i

^r5 v (a ?

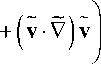
= -V p + V v ,

i = 1,2.     (11)

Вариант (6) принимается для медленных (куда и относятся микрофлюидные течения), а вариант (7) для быстрых течений. В нашем случае остановимся на варианте (6) микрофлюидных течений.

После подстановки (3)–(6) в уравнение (2) и учета преобразования дифференциальных опе-

9   1 5 v 1 v раторов — =---, V =—V получается следую- d t To d t       L0

щее уравнение:

При равенстве чисел Рейнольдса Re 1 = Re₂ уравнения (11) неразличимы. Степени свободы вариации процессов скрыты в числе Рейнольдса (10), в котором четыре параметра: плотность ρ , характерный размер L ₀ , характерная скорость V ₀ и сдвиговая вязкость η , — главное, сохранить постоянство числа Рейнольдса Re = const. Например, два процесса подобны, если у одного из них плотность и вязкость вдвое больше, чем у второго и т. д.

Поясним технику работы описанного принципа подобия, где в рамках модели (11) фигурирует только одна безразмерная постоянная — число Рейнольдса Re. Пусть, при Re _ const выбрана модельная задача с размерными коэффициентами L ₀ и V ₀ . Тогда, согласно [2, с. 88], поле вектора скоростей в этой модели определяется выражением

л

v , = V f -^,Re .

I ^{L O} i      )

~

Здесь f ( ) — функция, выражающая v из уравнения (11), остающаяся, естественно, инвариантной при Re _ const (напомним, что, по опреде- vr лению, —1- _ v , — _ r ).

V 0 1         L 0 1

Для моделируемой задачи с параметрами L ₀ и V ₀ поле вектора скоростей определяется подобным выражением

Л v = Vf    ,Re .

I L02     )

Поделив выражение (12) на (13), получаем

про-

vv порцию —1- = —, из которой определяется поле

V 0₁ V 0₂

скоростей моделируемой задачи

= ' Л 2                 1 .

V _{0 1}

Аналогичную формулу можно записать для определения давления в жидкости. Пусть, в модели и в моделируемом процессе давление p ₁ , p ₂ определяется выражением [2, с. 88]

A

η_iV ₀

p ^_ T"

L _{0 i}

f " r- ,Re , i = 1,2. I L о ,     )

Здесь в отличие от [2] размерный коэффициент в (15) взят в виде (6), а не (7). Функция f " ( ) выражает поле безразмерного давления p из уравнения (11) и также является инвариантной при Re _ const. Из (15) окончательно получаем

Р 2 = Р ,

L 0₁ η 2 V 0₂

L 0 2 η 1 V 0 1

Еще раз подчеркнем, что при моделировании вследствие постоянства числа Рейнольдса Re из

(10) должно выполняться условие

^Р , ^L 0 , V _ ^Р 2 ^L 0₂ ^V 0₂

η ₁        η ₂

Отметим также, что в выражениях (14) и (16) стоящие справа поля и коэффициенты должны быть известны.

Теперь, решая поставленную в работе задачу, можно выбрать модель с параметром L ₀ с нужным масштабом, к примеру в α раз большим ( L о _ aL _0з ), чем в оригинале. Этого можно достичь множественным образом, варьируя один параметр модели и оставляя другие постоянными.

Например, через плотность р, _ — р2, либо через α сдвиговую вязкость модели п, = an2. Можно варьировать два, три или все четыре параметра модели, оставляя в (10) и (17) число Рейнольдса постоянным и равным числу Рейнольдса моделируемого объекта.*)

Выражение (9) можно упрощать в зависимости от величины числа Рейнольдса. Очевидно, что при малых числах Рейнольдса Re << , левой частью в (9) можно пренебречь, после чего приходим к стационарному линейному уравнению Стокса

V v _ V p .

Либо, если учесть временнýю производную, но пренебречь малым в этом случае нелинейным членом ( v -V ) v , приходим к нестационарному линейному уравнению Стокса

dv __ ~2~ Re^r _-Vp + V v .

d t

При больших числах Рейнольдса уравнение (9а) можно свести к уравнению Эйлера, пренебрегая вязким членом:

dv ~\~   ~~

— + (v - V) v _ -V p. d t

Выше были приведены методы теории подобия применительно к несжимаемой вязкой жидкости, когда задача сводилась к использованию единственного безразмерного критерия подобия — числа Рейнольдса. Однако в механике жидкости зачастую присутствует ситуация, когда модель описывается двумя и более безразмерными критериями подобия [1, 2]. Так, в случае нестационарного движения жидкости, ее кроме уже приведенных параметров L0 , V0 , ρ и η можно характеризовать еще значением какого-либо характерного для этого движения интервала времени τ . При колебательном характере процесса этим временем может являться период колебаний. Из пяти приведенных величин можно составить не один, а два безразмерных критерия подобия: число Рейнольдса и число Струхаля S [2, с. 89]

V 0 τ S = .

L ₀

В случае учета силы тяжести используется такой критерий подобия, как число Фруда, в сжимаемой жидкости появляется еще один критерий подобия — число Маха и т. д. (см. [6, с. 165]).

ВЫВОДЫ

В настоящей работе для преодоления вычислительных трудностей было рассмотрено моделирование методом подобия исходной физической модели течения вязкой сжимаемой жидкости в капилляре моделью, позволяющей избежать этих трудностей. Для этого рассмотрена возможность сведения общего уравнения Навье—Стокса к уравнению для вязкой несжимаемой жидкости.

Было проведено упрощенное моделирование с одним безразмерным критерием подобия — числом Рейнольдса. Рассмотрены детали моделирования. Приведены другие возможные для исходной модели безразмерные критерии подобия.