Некоторые особенности моделирования систем молниезащит на космодромах

• [11]    исследованы особенности системы молниеза-щиты индийского стартового комплекса для РН. В рамках этой работы представлены исследования особенностей математического моделирования распределённых систем молниезащит на космодромах на базе цилиндрических и тросовых молни-еприёмников.

Постановка задачи. Схема модели системы молниезащиты на космодроме в виде плана показана на рис. 1. Устройство 5, связанное с РН 6 на старте, представляется в виде металлической фермы. Считаем, что металлическая ферма 5 и РН 6 имеют в сечениях соответственно квадрат / прямоугольник и цилиндр.

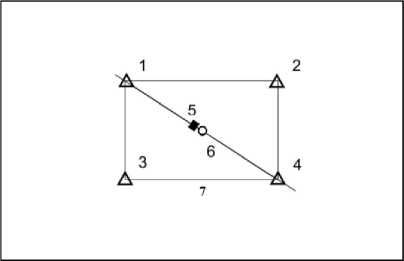
Рис. 1. Схема системы молниезащиты на космодроме: 1 – 4 – башни с цилиндрами и тросами на них по контуру; 5 – устройство, связанное с РН 6 на старте; 7 – тросы

Основные исследования проводятся для 2-х вариантов схем с возможным учётом комбинации стержней-цилиндров и тросовых молниеприёмни-ков: 1) башни с металлическими цилиндрами в её верхней части и тросами по контуру; 2) башни с изолированными цилиндрами (в виде изоляторов) в её верхней части и тросами по контуру. Для постановки этой задачи важно отметить следующее. Результаты расчётов показали [12, 13], что при решении внешней краевой задачи на основе применения метода инверсии для полубесконечных областей (МИПО) и при решении внутренней краевой задачи

• [14]    на основе условия д^/д=0 вместо ^=0 на бесконечности в целом погрешность этих расчётов для аналогичных объектов была незначительная, но для определённой части области [13].

В связи с тем, что в этой работе исследуется распределённый объект и не учитывается краевой эффект облака, поэтому внешняя краевая задача сводится к внутренней на основе условия д^/д n =0. Исследования распределённого объекта проводятся в вертикальной диагональной плоскости стартовой площадки от 1-ой до 4-ой башни (см. рис. 1). При математическом моделировании системы молние-защиты используется схема, показанная на рис. 2.

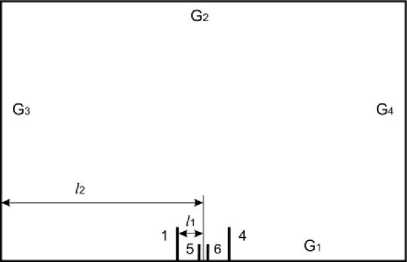
Рис. 2. Схема моделирования области C ( х , у ) системы молниезащиты на космодроме (цифровые обозначения как на рис. 1)

Границы области С ( х , у ) следующие: G 1 -плоскость в виде поверхности земли F ( ху ); G₂ -нижняя граница облака V ( ху ) в виде плоскости относительно поверхности F ( x, у ); G₃, G₄ - границы искусственного ограничения С ( х , у ), связанны с условием типа д^/д n = 0 (не учитывается краевой эффект от V ( ху )). Для каждого из двух вариантов модели соотношения следующие:    l 1 = l ₁₀=const;

l ₂= 1 ₂₀=const; высота H 1 = H ₁₀=const (от F ( ху ) до нижней границы V ( x, у )); высота башней H ₂= H ₂₀=const; высота металлической фермы и РН равны H ₃= H ₃₀=const; высота металлических или изолированных цилиндров на башнях H 4 = H 40 =const (на вершинах цилиндров закреплены тросы).

На первом этапе математического моделирования считается, что величина H10 существенно превышает суммарную высоту H20 и H40. В связи с этим можно считать, что вместо реальных соотношений размеров исследуемых объектов (башней с цилиндрами и тросами, металлической фермы и РН) их можно представлять линиями, но с учётом их высот. При решении задачи на этом этапе определяются поле у и эквипотенциальные поверхности уi=const с шагом А^=const. Затем относительно высоты H1 на основе расчётов этого этапа выделяется некоторая область W(х,у) до уровня Hfv относительно поверхности F(ху). Это необходимо для того, чтобы на следующем этапе учесть соотношения исследуемых объектов. Для этого выполняется масштабирование части исходной области С(х,у) с возможностью определения W(х,у), причём вместо границы G2 появляется граница G22, являющаяся некоторой эквипотенциальной поверхностью уfv=const. Особенность выбора W(х,у) следующая: 1) на уровне Hfv выбранная поверхность уfv=const должна быть параллельна границе G2, чтобы было исключено влияние исследуемых объектов на распределение напряженности поля на этом уровне; 2) Hfv должна превышать max высоту этих объектов. Для области С(х,у) с учётом плоско-параллельной задачи поле распределения у определяется на основе решения уравнения Лапласа в виде

• □ ду /дх2 + ду /ду2; (х,у) е C(х,у).(1)

Граничные условия c учётом рис. 2 следующие (общие для 2-х вариантов):

• •    а границе G 1 :

V(х,у)=0, (х,у) е G1;(2)

• •    на границах G 3 , G 4 :

д^/дn=0, (х,у) е G3, G4;(3)

• •    на границе G 2 :

V(х,у)=Yc, (х,у) е G2;(4)

• •    на границах башен с цилиндрами 1 (G 11 ) и 4 (G₁₄), на металлической ферме 5 (G₁₅) и на РН 6 (G₁₆), заземлённых относительно F ( ху ):

V(х,у)=0, (х,у) е Gn, G14, G«, G16;(5)

где C ( х , у ) - исследуемая область, ограниченная G 1 - G 4 , G_n, G 14 , G 15 , G 16 .

На втором этапе математического моделирования определяются поле у и эквипотенциальные поверхности у i = const с шагом А^= const для выделенной области W ( х , у ) с исследуемыми объектами. Границы области W ( х , у ) следующие: G 21 - граница в виде части G 1 ; G 22 - граница на уровне H f _v в виде некоторой эквипотенциальной поверхность у f = const ; G₃₁ - граница в виде части G₃; G₄₁ - граница в виде части G₄; G 11 b , G₁₄ b - границы соответствующие башням 1 и 4; G 11 d , G₁₄ d -границы соответствующие цилиндрам на башнях 1 и 4; G 11 е , G_{14 e} - границы соответствующие тросам на цилиндрах; G₁₅ g , G₁₆ q - границы соответствующие металлической ферме и РН. Для масштабируемой области W ( х , у ) поле распределения потенциала ^ определяется на основе решения уравнения Лапласа (1). Граничные условия (одинаковые для каждого из 2-х вариантов этого этапа) записываются следующим образом:

• •    на границе G₂₁:

V(х,у)=0, (х,у) е G21;(6)

• •    на границах G 31 , G 41 :

dV/dn=0, (х,у) е G31, G41;(7)

• •    на границе G 22 :

V(х,у) = ^01, (х,у) е G22;(8)

• •    на границах башен Gn b , G₁₄ b , на G₁₅ g и на РН G 16 q :

V( x , y )=0, ( x , y ) e G 11 ь , G 14 ь , G 15 g , G 16 q ; (9)

Дополнительное граничное условие для 1-го варианта задачи с металлическими цилиндрами G_n d , О_ш следующее:

V( x , y )=0, ( x , y ) e G 11 d , G 14 d, (10)

Для этого варианта задачи тросы на металлических цилиндрах совпадают с их вершинами и не учитываются, так как они имеют одинаковый потенциал. Дополнительное граничное условие для 2-го варианта задачи с изолированными цилиндрами и с тросами G 11 е , G₁₄ e следующее:

V( x , y )=0, ( x , y ) e G_U е , G 14 e . (11)

Для этого варианта задачи учитываются только тросы, находящиеся на верхних частях изолированных цилиндров. Считаем, что потенциалы V 0 и v₀₁ на границах G₂ и G₂₂ возникают в условиях электрических полей в атмосфере. При этом исследуются электростатические поля (ЭП) при условиях, что внешнее поле, прикладываемое к исследуемым объектам существенно мало, т.е. подразумевается отсутствие объёмных электрических зарядов в атмосфере исследуемых областей C ( x , y ) и W(x , y ).

Результаты численных расчетов. Особенности дискретных математических моделей для каждого этапа расчёта заключаются в том, что исходные области C ( x , y ) и W ( x , y ) представляются дискретными с регулярной прямо-угольной сеткой (A x =A _y ), например, как в [12, 13]. При расчетах в области C ( x , y ) не учитываются размеры в горизонтальных сечениях исследуемых объектов, так как они пренебрежимо малы по сравнению с шагом Δ сетки по координатам x , y (например, между G₃ и G₄ расстояние в пределах 2000 м, а высота до V ( x,y ) порядка 1000 м). Учитываются только высоты этих объектов. Для каждой из расчётных областей C ( x , y ) и W ( x , y ) во внутренних узлах сетки выполняется условие сходимости итерационного метода Гаусса-Зей-деля. В этих узлах дискретных областей потенциал v ij рассчитывается с помощью численного метода, например, ускоренного метода Либмана с учётом уравнения Лапласа в конечно-разностных аппроксимациях как в [12]. На границах G i областей C ( x , y ) и W ( x , y ) потенциалы v ij рассчитываются с учетом конечно-разностных ап-проксимаций для сформулированных условий. Численные расчёты ЭП для башен с металлическими цилиндрами в их верхних частях и с тросами показаны на рис. 3.

Расчёты представляются в безразмерном виде, а именно, потенциалы определяются как Vi =Vi/^0; где ^0 - базовое значения потенциала на границе области, а компоненты напряженности электрического поля в виде E*x= –∂ψ*/∂x*; E*y= – ∂ψ*/∂y*. Аналогично записываются безразмерные параметры и для других величин. Важно отметить, что при исследованиях распределенных систем молниезащит определяются ЭП с учётом распределения потенциала ψ и эквипотенциальных поверхностей, а также поверхности равных напряженностей поля Ei в виде уравнений Е,=const. Численные расчёты ЭП башен с изолированными цилиндрами в их верхних их частях и с тросами показаны на рис. 4.

а)

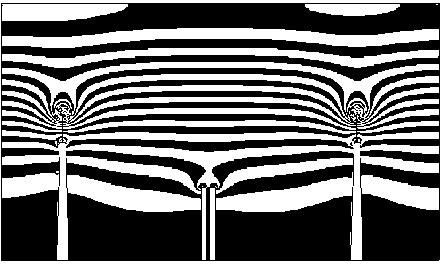
б)

Рис. 3. Распределение эквипотенциальных поверхностей ЭП с шагом Av (а) и поверхностей равных напряженностей поля с шагом NE (б)

а)

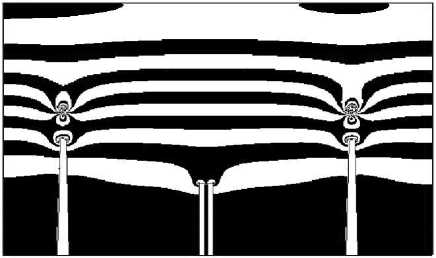
б)

Рис. 4. Распределение эквипотенциальных поверхностей ЭП с шагом Av (а) и поверхностей равных напряженностей поля с шагом A E (б)

Сравнительный анализ результатов численных расчётов на рис 3б и рис. 4б для поверхностей равных напряженностей поля E i показывает следующее:

• 1)    Для первого варианта расчёта напряжённость E is в среднем порядка 1060,5 на вершинах металлических цилиндров с тросами, а в верхней части РН (в угловых зонах) напряжённость E sp в среднем около 316,5.

• 2)    Для второго варианта расчёта напряжённость E it в среднем порядка 1581,5 на тросах, а в верхней части РН (в угловых зонах) напряжённость E tp в среднем около 599,5.

Сравнительный анализ систем молниезащит показывает следующее: 1) по первому варианту отношение E is / E sp в пределах 3,4 раза; 2) по второму варианту отношение E it / E tp приблизительно равно 2,6 раза. Численные расчёты на основе подхода электростатики позволяют оценить особенности распределённых систем молниезащит на стартовых площадках с учётом башен, цилиндров и тросов, а также позволяют сделать следующий вывод: башни с изолированными цилиндрами в верхних их частях и с тросами по контуру по сравнению с молниезащитой, имеющей в верхней части металлические цилиндры с тросами, позволяют повысить напряженность поля приблизительно в 1,5 раза, т.е. ( E it / E is * =1581,5/1060,5). Учитывая эту особенность распределённой системы молниеза-щиты с изолированными цилиндрами и с тросами по контуру, тогда проверим возможность полного изолирования башен и с применением тросов с условием, что их высота определяется суммой высот H₂₀ и H ₄₀. Оценим влияние этого условия на ЭП, так как для систем молниезащит важно увеличение максимальных значений напряженности E i на молниеприёмниках. Численные расчёты для исследуемой системы показаны на рис. 5.

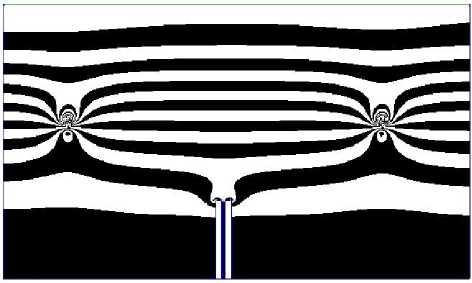
Рис. 5. Распределение поверхностей равных напряженностей поля с шагом NE

Анализ полученных результатов исследуемой молниезащиты показывает, что величины Eito и Etp0 в среднем уменьшилась в пределах 7-8%, т.е. эффекта увеличения напряженности Ei на молние-приёмниках не наблюдалось. Из полученных результатов математического моделирования следует, что максимальная напряжённость Ei на молние- приёмниках превосходит напряженность на объектах защиты, поэтому можно провести исследования, например, для оценки возможного удара молнии в систему молниезащиты на старте, как это было с применением шаттла, например, для «Атлантиса», однако оценить возможность удара молнии с помощью используемого подхода в стартовый комплекс как в [1] невозможно. Для этого случая оценить возможность удара молнии в стартовый комплекс как в [1] можно на основе решения уравнения эллиптического типа для электрической функции потока ц [15] аналогичного уравнению Лапласа:

д ц /д x ² + д ц /д у ² = 0.                  (12)

Численные расчёты ЭП на основе уравнения (12) и с учётом рис. 1 и рис. 2 для некоторой области W k (x , у ) показаны на рис. 6.

а)                          б)

Рис. 6. Распределение поверхностей функции потока ц i = const с Ац = const

При этом на рис. 6а показаны 30 функций потока ц i ; рис. 6б соответственно 100 функций потока ц i с учётом, например, равномерного распределения функций потока ц i из верхней границы области W k ( x , у ). Из результатов, представленных на рис. 6, можно оценить количество функций потока ц i , входящих в выбранную часть исследуемого объекта или в стартовую площадку. Например, в стартовую площадку (часть F ( x,y ) области W k ( x , у )) до молниеприёмника входят 10 функций потока ц i и одна частично в молниеприёмник и в F ( xy ). Тогда в процентом отношении 11% из 100 функций потока ц i могут полностью и частично входить в стартовую площадку до молниеприёмника.

Выводы:

• 1.    Численные расчёты на основе подхода электростатики позволили оценить возможности 2-х вариантов распределённых систем молниезащит на стартовых площадках и установить, что молние-приёмники на базе изолированных цилиндров и с тросами по контуру по сравнению с аналогичными молниеприёмники, но с металлическими цилиндрами и с тросами, позволяют повысить напряженность поля приблизительно в 1,5 раза.

• 2.    Численное моделирование технического решения в виде распределённой системы молниеза-щиты на базе полного изолирования башен и с применением тросов в их верхних частях при условии равенства высот с исследуемыми и существующими системами молниезащиты показало, что эффекта увеличения напряженности E_i на молние-приёмниках не наблюдалось.

• 3.    Представленные расчёты не исключают возможности оценивания и выявления особенностей

  
  
  
  

• 6.

• 7.

• 8.

• 9.

существующих систем молниезащит на космодромах на основе использования уравнения Лапласа (1) и/или уравнения (12) в зависимости от решаемой задачи.