Некоторые особенности оптической картины течения в пограничном слое на модели профиля при больших дозвуковых скоростях

В аэродинамике при изучении течений широко используются оптические, в частности теневые, методы, которые позволяют получать качественные и количественные данные о стационарных и нестационарных процессах в прозрачных средах, где показатель преломления света, по каким-либо причинам меняется [2,8,13]. Важным достоинством оптических методов является то, что результаты получаются без ввода, в изучаемую область каких-либо датчиков, т.е. без дополнительных внешних возмущений, искажающих первоначальную картину течения.

В основе теневых методов исследования течений газов лежит явление рефракции — отклонения световых лучей в связи с изменением показателя преломления п в исследуемой среде. Показатель преломления связан с плотностью р известной формулой, которая для газов имеет вид п — 1 = кр,

«Московский физико-технический институт (национальный исследовательский университет)», 2019

где к — константа Гладстона—Дейла, имеющая для воздуха значение к = 0.22635 см3/гр. Величина отклонения светового луча в перпендикулярном направлении у от направления его распространения ж характеризуется производной d2у/dx2, которая пропорциональна градиенту коэффициента преломления: d^y/dx21 ~ dn/dy. Согласно соотношению (1), величина градиента коэффициента преломления пропорциональна градиенту плотности, следовательно, распространение луча света определяется уравнением d2 y/dx2 = kdp/dy.

Наиболее простым и распространенным теневым методом исследования пограничного слоя является прямой теневой метод. Если градиент плотности, нормальный к световому лучу неравномерен, то соседние лучи, проходящие через газовую неоднородность, будут отклоняться различно и сходиться или расходиться на выходе из рабочей части аэродинамической трубы (АДТ). При этом изображение будет образовываться на экране, помещенном за пределами рабочей части в плоскости фокусировки (рис. 1).

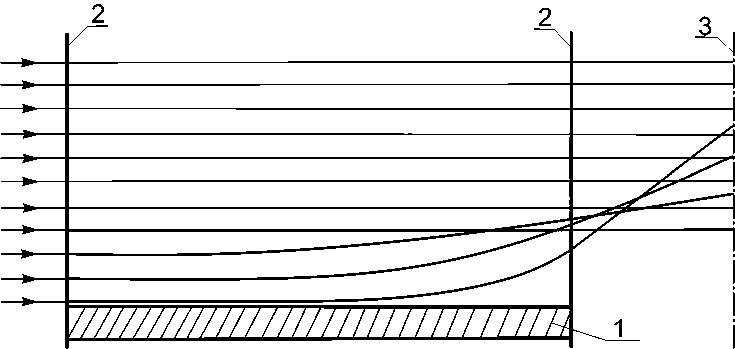
Рис. 1. Схема рефракции световых лучей: 1 — поверхность профиля; 2 — оптические окна; 3 — плоскость фокусировки теневого прибора

Можно показать, что изменение освещенности экрана в грубом приближении пропорционально степени изменения градиента плотности. По указанной причине прямой теневой метод предпочтительнее метода Теплера (в котором изменение освещенности приближенно пропорционально градиенту плотности) в тех случаях, когда необходимо изучить некоторые явления течений [8]. Оказалось, что стандартный прямой теневой метод можно усовершенствовать и с успехом использовать для определения ламинарно-турбулентного перехода и оценки эффективности, применяемых на практике, турбулизаторов пограничного слоя [4-6]. При этом замечено, что при использовании прямого теневого метода для исследования характера течения в пограничном слое, состояние которого на поверхности обтекаемого тела является главным фактором, определяющим его сопротивление, наблюдаются оптические эффекты, которые нуждаются в объяснении. В настоящей работе выяснены причины появления и дано объяснение оптических эффектов, наблюдаемых в АДТ в процессе исследования пограничного слоя на профилях прямым теневым методом.

2.    Характерные особенности оптической картины течения в пограничном слое при использовании прямого теневого метода

Прямой теневой метод часто применяется при оптических исследованиях пограничного слоя, поскольку течение в нем характеризуется наиболее резким изменением градиента плотности в направлении нормали к поверхности обтекаемого тела.

Исследования проводились в трансзвуковой аэродинамической трубе Т—112 ЦАГИ на модели, выполненной в виде прямоугольного крыла с хордой 200 мм и размахом 599 мм. Сечение крыла соответствовало геометрии сверхкритического профиля П—184—15 максимальной относительной толщины 15%. В испытаниях профиль устанавливался между оп- тическими окнами АДТ перпендикулярно направлению набегающего потока и освещался плоскопараллельным пучком света вдоль размаха. Картина течения фиксировалась теневым оптическим прибором ИАБ—451 с фотографической приставкой. Прибор сфокусирован на экран (плоскость фокусировки), расположенный за пределами рабочей части АДТ, см. рис. 1. На полученных при различных числах Маха М^ фотоснимках (рис. 2 и 3) хорошо виден пограничный слой. Для определенности все результаты приведены для угла атаки а = 2°.

Важно отметить, что при стандартных оптических исследованиях на получаемых фотоснимках можно выделить две характерные особенности, которые связаны с эффектами, требующими физического объяснения.

• 1.    Возникновение светового блика в диффузорной части профиля (рис. 2).

• 2.    Размывание светового блика при больших числах М^ (рис. 3).

• 3.    Физические причины появления оптических эффектов, наблюдаемых при исследованиях пограничного слоя прямым теневым методом

На внешней границе пограничного слоя в диффузорной части профиля отчетливо видна тонкая светлая полоска - световой блик (рис. 2).

Рис. 2. Световой блик (линза) в диффузорной части профиля

Рис. 3. Размывание световой линзы при увеличении числа Мт

В экспериментах замечено, что при увеличении числа М^ световой блик постепенно размывается. Область размытия начинает формироваться в окрестности задней кромки профиля и расширяется далее в сторону передней кромки.

С целью объяснения характерных оптических эффектов проведена серия расчетов обтекания профиля П—184—15 при угле атаки а = 2°, различньіх числах Мго в диапазоне чисел Рейнольдса Re = (2.3-2.8) • 106. Расчеты проводились в рамках уравнений Навье Стокса сжимаемого теплопроводного газа с SST-моделью турбулентности при помощи компьютерного кода ANSYS СҒХ. Использовались стандартные граничные условия прилипания и условие адиабатической стенки. Обтекание считалось полностью турбулентным, поскольку при испытаниях в АДТ применялись турбулизаторы пограничного слоя, которые наклеивались на поверхность модели в окрестности передней кромки.

Для численного моделирования вокруг геометрического контура профиля была построена стандартная СН-сетка с количеством ячеек, примерно равным 3 • 105, со сгущением в областях больших градиентов давления, пограничного слоя и следа за профилем. Высота первой ячейки у поверхности составляла примерно 1/106 хорды профиля с.

Результаты расчетов обтекания профиля П 184—15 при значении угла атаки a = 2°, числа Маха М^ = 0.73 в двух различных сечениях приведены на рис. 4 и 5. На них фиолетовым цветом показан профиль плотности р(у), а зеленым — профиль скорости п(у). Синей штриховой линией обозначена высота пограничного слоя 8.

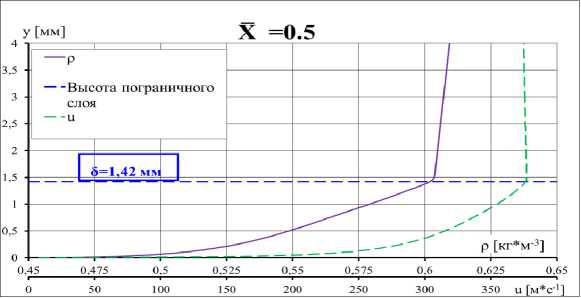
Рис. 4. Профили скорости и плотности в сечении х = 0.5 (середина профиля) при a = 2°, М^ = 0.73

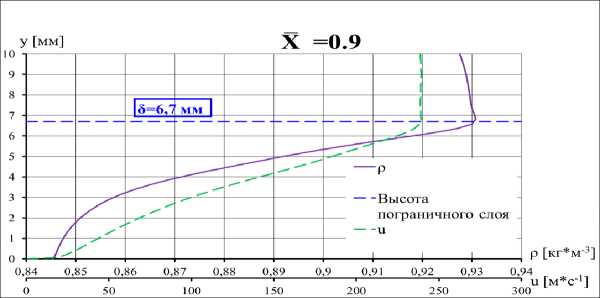
Рис. 5. Профили скорости и плотности в сечении х = 0.9 (диффузорная часть профиля) при a = 2°, М _х = 0.73

Аналогичные графики для числа М^ = 0.78, когда на верхней поверхности профиля уже имеется скачок уплотнения, приведены на рис. 6 и 7.

На всех приведенных графиках в обоих сечениях хорошо заметен характерный излом зависимости р = р(у) на границе пограничного слоя, толщина которого возрастает как с увеличением числа М^, так и по мере приближения сечения к задней кромке профиля. С увеличением в диффузорной части профиля скорость на внешней границе пограничного слоя U_B убывает, угол наклона dp/dp линейного участка профиля р(у) уменьшается и становится отрицательным в области, где U_B<  U^. При увеличении числа М^ излом графика зависимости р = p(p) постепенно сглаживается. Ниже установлены причины, по которым указанные особенности течения приводят к появлению световой линзы и ее размыванию при больших числах М^.

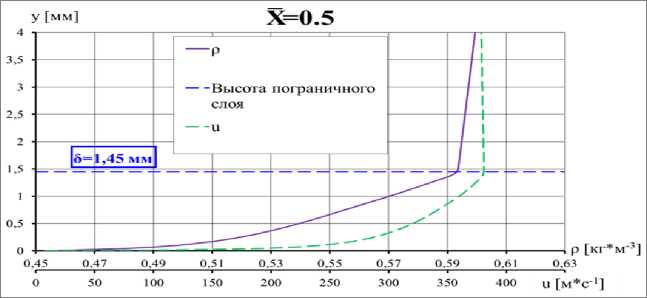
Рис. 6. Профили скорости и плотности в сечении ж = 0.5 (середина профиля) при а = 2°, М^ = 0.78

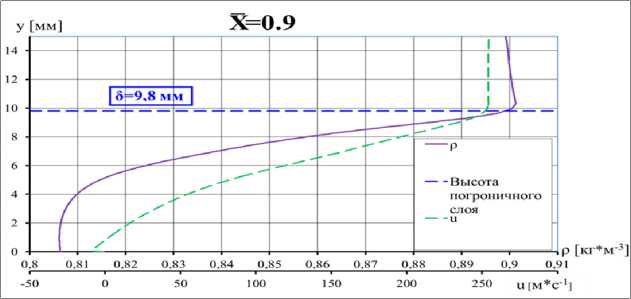
Рис. 7. Профили скорости и плотности в сечении ж = 0.9 (диффузорная часть профиля) при а = 2°, М^ = 0.78

Известно, что в пограничном слое поперечный градиент давления мал, т.е. dp/dy = о(1), откуда из уравнения состояния p = pRT получаем, что в пограничном слое р ~ 1/Т. Температура в пограничном слое по мере удаления от стенки падает [7], следователвно, имеет место неравенство dp/dy = > 0.

Получим теперь зависимость знака производной dp/dy во внешнем невязком потоке. Из «закона кубов» [4] следует, что при трансзвуковых скоростях течение приближенно (с точностью до куба изменения энтропии) можно считать изоэнтропическим. В этом случае выполняется соотношение p = р⁷, где показатель адиабаты у для воздуха равен 7/5. Тогда с учетом уравнения состояния получаем, что р ~ Т ^5/2, т.е. знаки производных dp/dy и dT/dy совпадают. Во внешнем потоке из уравнения Бернулли

+      = const

• 2 у — 1

при отсутствии возвратных течений (U > 0) следует, что dT   dU dy     dy

Таким образом, заключаем, что во внешнем потоке производные плотности dp/dy и скорости dU/dy имеют противоположные знаки.

В конфузорной (разгонной) части профиля скорость вблизи поверхности больше скорости на бесконечности, поэтому dU/dy < 0, а следовательно, dp dy

> 0,

что видно из расчетов, приведенных на рис. 4 и 6 (ж = 0.5).

Иная картина (см. рис. 5 и 7) наблюдается в диффузорной части профиля в области торможения потока (ж = 0.9), где скорость вблизи поверхности меньше скорости на беско-ІІ0ЧІІОСТИ. т.е. dU/dy >  0. а слелователыю.

dp dy

< 0.

Итак, установлено, что градиенты плотности dp/dy в пограничном слое и внешнем невязком потоке могут иметь противоположные знаки. Данное обстоятельство приводит к тому, что в области торможения потока, где U < U^, лучи света в пограничном слое вследствие рефракции отклоняются вверх, а во внешнем потоке вниз, что вызывает появление в окрестности внешней границы пограничного слоя светового блика или световой линзы — эффекта самофокусировки световых лучей.

Эффект размывания светового блика при увеличении числа М^ связан с усилением ин тенсивности скачка уплотнения, который вызывает усиление вихревого движения за ним. Образовавшиеся вихри перемешивают поток, выравнивая (по мере роста числа М^) температуру в пограничном слое. Зависящие от градиента температуры, градиенты плотности ослабевают и становятся недостаточными для рефракционного рассеяния световых лучей, что и приводит к постепенному размыванию светового блика.

4.    Заключение

С помощью прямого теневого метода проведены оптические исследования обтекания модели аэродинамического профиля при больших дозвуковых скоростях. Выявлены две характерные особенности получаемой картины течения: появление светового блика в окрестности внешней границы пограничного слоя и его постепенное размывание с увеличением числа Маха.

Установлено, что образование светового блика в диффузорной части профиля связано с различием знаков градиентов плотности в пограничном слое и во внешнем потоке, вследствие чего лучи света в этих областях отклоняются в разные стороны, что приводит к эффекту самофокусировки светового пучка.

Размывание светового блика при больших числах Маха обусловлено ростом интенсивности скачка уплотнения и усилением вихревого течения за ним, что вызывает ослабление градиента плотности в пограничном слое и постепенное размывание светового блика.