Некоторые особенности задачи нелинейной оптимизации

С различными задачами оптимизации человек встречается во многих ситуациях повседневной жизни и профессиональной деятельности. Каждое разумное действие можно считать в определенном смысле и оптимальным, так как оно выбирается после сравнения с другими вариантами.

Определение экстремума, т.е. максимума или минимума функции одной переменной без дополнительных условий и при достаточно простой функции давно решенная задача. Использование дифференциального исчисления сделало эту задачу классической задачей школьной программы. Под достаточно простой функцией имеется в виду непрерывная гладкая функция, корни которой и корни производной которой легко определяются, не требуя применения численных методов.

Задача оптимизации функции нескольких переменных при наличии ограничений, т.е. функций, связывающих эти переменные, до сих пор не всегда легко решается из-за множества особенностей.

Например, задача линейного программирования или задача оптимизации линейной функции при наличии линейных ограничений на область изменения этих переменных решена однозначно для всех возможных случаев. Симплекс-метод даёт исчерпывающий ответ в задачах любой разумной размерности.

Описание особенностей

Задача оптимизации функции f(x), где х = (х 1 , ...,х_п)^Т , с дополнительными условиями связи переменных g j (x') = {>, <} 0,j = 1 ,т, когда хотя бы одна из функций f(x) или g j (x) является нелинейной называется задачей нелинейного программирования или нелинейной оптимизации. Функцию f(x), экстремум которой необходимо найти, часто называют целевой функцией, а условия связи g j (х) -ограничениями задачи. Множество значений переменных, удовлетворяющих всем ограничениям, называют допустимой областью. При этом, ограничение является активным в точке, если выполняется по знаку «=», в противном случае – пассивным. От допустимой области часто требуется выполнение условий регулярности. Эти условия могут быть сформулированы по-разному [1, 3, 4, 6, 7, 8, 9, 10, 12, 13, 14, 16]. Простейшими из этих условий являются условия регулярности Слейтера [1, 6, 7, 8, 13, 16, 18], которые требуют существования хотя бы одной внутренней точки допустимой области. Этим свойством обладает допустимая область, задаваемая системой линейных неравенств [6, 8, 18]. Линейная независимость градиентов ограничений в стационарной точке эквивалентна выполнению условий регулярности [3, 4, 7, 8, 9, 10, 12].

Решение задачи нелинейной оптимизации для различных функций f (x) и g j(x) и различных условий связи с разной степенью подробности можно найти в различных источниках [1-12, 15-18]. Среди различий в описании задачи и её решений

f(x) ^ min(max)

ХЕХ

можно выделить следующие особенности: формулировка функции Лагранжа; запись ограничений; требования к множителям Лагранжа.

Вообще частный случай нелинейной задачи

f(x) X = {xlgi(x) = 0, i = 1 ,т},        (1)

когда f(x) - нелинейная функция, а g i (x) - линейные функции может быть легко сведен к задаче безусловной оптимизации при т < п. В случае нелинейности g i (x) такой исход также возможен.

Однако, полученные соотношения не всегда приводят к эффективным решениям.

Решение задачи (1) для произвольных функций был предложен Ж.Л. Лагранжем ещё в конце 18 века [1, 3, 11, 16, 17, 18]. Введение классической функции Лагранжа

т

Цх,^ = f⁽x) + ^X_ig_i⁽x⁾,

где Л = (Л 1 ,.,Л_т~)^Т — множители Лагранжа, также сводило задачу на условный экстремум к задаче безусловной оптимизации. Очень долго метод множителей Лагранжа формулировался с классической функцией Лагранжа, что верно только если ограничения задачи обладают свойством регулярности [1]. Во многих источниках рассматривается только классиче-

( 2 )

i=1

ская функция Лагранжа [2, 6, 17, 18], а об условиях регулярности упоминается вскользь. Поскольку не всякая допустимая область обладает свойством регулярности, и не всегда это можно проверить без дополнительных сложностей, то правильнее было бы использовать обобщенную функцию Лагранжа [1, 3, 4, 7, 8, 9, 10,11, 16]:

т

L(x,Л о ,

Л) = Л о f(x) + ^ Ajgj(xy

( 3)

j=1

При этом следует рассматривать два случая: Л о = 0 и Л о Ф 0 (Л о = 1 ). Условия регулярности гарантируют Л о Ф о и справедливость классической функции Лагранжа.

Постановка задачи нелинейного программирования может приводить к раз-

личным формам записи исходных ограничений и используемой функции Лагранжа. В классической задаче на условный экстремум, когда все ограничения равенства, можно встретить следующие записи ограничений:

g^x) = bj - (p^x) = о ~  [2, 5, 17,18]

g j (x) = _V j (x)-b j = о ~  [1,3,4,7,8,9,10,14,15,16]

Соответственно в функцию Лагранжа (обобщенную или классическую) они входят с противоположными знаками.

Поскольку при решении классической задачи множители Лагранжа не ограничены знаком, т.е. могут быть разных знаков, лишь бы все одновременно не обращались в ноль, то выполнение необходимых и достаточных условий экстремума приводит к одинаковым результатам. Это чуть позже будет показано в примере 1.

В задачах с ограничениями неравен- типа, аналогично, часто используются за-ствами или ограничениями смешанного писи:

gj(x} = bj — pj(x}< 0~ [2, 17, 18], gj(x) = p j(x) -bj< 0 ~ [1, 4, 7, 8, 9, 10, 11, 13, 14, 15, 16].

Так как знаки множителей Лагранжа теперь играют определяющую роль: будет это точка локального максимума или минимума, или не будет экстремальной точкой, то необходимо очень внимательно записывать необходимые и достаточные условия экстремума, а также саму функцию Лагранжа. Например, в [2] используется функция Лагранжа в виде L(x,A) = f (x) — Т т 1 Л i (b j — p j (x)) , стационарные точки, которой не отличаются от стацио-

нарных точек классической функции Лагранжа (2).

Рассмотрев многочисленные формы записи и функции Лагранжа, и ограничений, сформулируем наиболее простые, понятные составляющие нелинейной задачи оптимизации. Все необходимые соотношения, используемые при решении, представлены в таблице 1.

Во-первых, все ограничения будем записывать в виде:

gj (x) = Pj (x) — bj = 0 или gj (x) = Pj (x) — bj < 0.

( 4 )

Во-вторых, всегда будем использовать обобщенную функцию Лагранжа (3) и необходимые условия экстремума 1-го порядка. Полученная система решается для двух случаев Л ₀ = 0 и Л о Ф 0 , если не удается установить условия регулярности.

Далее, для всех найденных стационарных регулярных и нерегулярных точек проверяются достаточные условия 1-го и 2-го порядка. Если достаточные условия экстремума не выполняются, следует проверить необходимые условия 2-го порядка, и либо продолжить исследования, либо установить отсутствие экстремальной точки. В заключении остаётся вычислить значение функции в экстремальной точке.

Таблица 1. Решение задачи нелинейной оптимизации

Задача нелинейной оптимизации
Постановка задачи	f (x) ^ min(max) f(x); хеХ ( g j (x) = 0\ Г j = 1 ,m J	f(x) ^ min(max)f(x); хех 1 g j (x)< 0,\ Г j = 1 ,m J	f(x) ^ min(max) f(x); х_(   g j (x) = 0,j = 1 'k j ( g j (x)< 0,j = k + 1 gm)
Обобщенная функция Лагранжа	т L(x,Л 0 ,Л) = Л 0 f(x) + '^Л j g j (x), j= 1 (x * ,Л * 0 ,Л*} — стационарная точка функции Лагранжа
Необходимые условия   экстре мума 1-го порядка	дL(x * ,Л 0 ,Л*) dxi____ ' i = 1 ,п g j (x*') = 0 ,j = 1 ,m	дL(x*'Л 0 'Л*') dxi____ ' i = 1 ,n g^x ' ) < 0 ,j = 1 ,m	dL(x * 'Л 0 ,Л*) = dxi____ ' i = 1 gn g j (x*} = 0 'j = 1 'k g j (x*) < 0'j = k + 1 'm
		л * > 0,j = 1 ,m;min ( л * < 0,j = 1, m;) V     max      / Л j g i (x) = 0,j = 1 ,m	л * > 0 'j = k + 1 gm; min (л * < 0 'j = k + 1 gm; max ) Л J g j (x) = 0 'j = k + 1 gm
Достаточные условия   экстре мума 1-го порядка	-	I - число ограничений равенств и активных ограничений неравенств: если 1 = п, Л’ * > 0 ,j е Ja- локальный min ;

		А < 0,j Е ]а- локальный max; если 1 < n или А не удовлетворяют достаточным условиям, проверить достаточные условия 2-го порядка; Ja — активные ограничения
Необходимые условия   экстре мума 2-го порядка	d 2 L(x*,А*') > 0т1п; (d 2 L(x * ,А*') < 0тах)
	dд j (x*') = 0 ,j = 1 ,т	dд j (x*) = 0, jeJ a ,X * > 0(Ц< 0) dдj(x*) < 0, jtJ a ,A i = 0	д ] (х*) = 0 ,j = 1 ,k, jEJ a ,A - > 0(А - < 0); dдj(x*} < 0,j EJ a ,A j = 0
Достаточные условия   экстре мума 2-го порядка	d 2 L(x * ,А *) > 0min; (d 2 L(x * ,А * ) < 0тах)
	dд j (x*') = 0 ,j = 1 ,т	dд^(x*) = 0, jEJ a ,A * > 0(А ] < 0) dд j (x * ) < 0, jEJ a ,A - = 0	dд j (x * ) = 0 ,j = 1 ,k, jEJ a ,A * > 0^< 0); dдj(x*) <  0,j EJ a ,A j = 0

Вычисление значения функции в точке х * локального экстремума

Выполнение всех шагов алгоритма покажем на примерах.

Пример 1. Найти экстремум функции /(х) = 2х 1 + 2х 2 , учитывая, что

X = {х|х ² + х 2 = 8 }.

Решение. Так как точка (0; 0) не являет-

ся решением задачи, то градиент ограни- 1

2 допустимой области, выполняются условия регулярности и А о ^ 0 , т.е. можно ис-

чения У д(х) = (

' 2 х

2 х

) ^ 0 во всех точках

пользовать классическую функцию Лагранжа. Рассмотрим два варианта учета ограничения в функции Лагранжа в таблице 2.

Таблица 2. Решение примера 1

1 вариант	2 вариант
Ь(х,А) = 2 х 1 + 2 х 2 + А(х 2 + х 2 — 8 )	L(x,А') = 2 х 1 + 2 х 2 + А( 8 — х 2 — х 2 )
Необходимые условия экстремума
L'Xl= 2 + 2 х 1 А = 0 L'X2 = 2 + 2 х 2 А = 0 х 2 + х 2 = 8	L'Xl= 2 — 2 х 1 А = 0 L'X2 = 2 — 2 х 2 А = 0 х 2 + х 2 = 8
Решение системы
(2; 2),А = — 1 /2 и (—2;— 2),А = 1 /2	(2; 2),А= 1 /2 и (—2 ; — 2 ),А = — 1 /2
Достаточные условия экстремума d 2 L = 2 А(dx 2 + dx22 )
d 2 L(2; 2) < 0 ^ тах; d 2 L(—2; — 2) > 0 ^ min	d 2 L(2; 2) < 0 ^ тах; d 2 L(—2; — 2) > 0 ^ min
f max = f(2 ; 2) = 8 ; f min = f(—2 ; — 2) = — 8

Как видно из примера, варианты отличаются лишь знаком множителей Лагранжа.

Пример 2. Найти экстремум функции /(х) = 3х 1 + 4х₂ , если

X = {х|х2 + х2 < 25; х 1х2 > 4; х 1 > 0; х2 > 0}.

Решение. Во-первых, для наглядности решим эту задачу графически:

д 1 (х) = х ² + х 2 — 25 < 0 - внутренность круга с центром в (0;0) и радиусом 5;

д₂(х) = —х 1 х₂ + 4 < 0,д 3 (х) = —х 1 <  0 , д₂ (х) = —х ₂< 0 - вместе задают область справа от гиперболы. На рисунке допустимая область заштрихована, показан градиент функции дrаdf(x') = { 3 ; 4 } и линия уровня 3х 1 + 4х₂ = 0 .

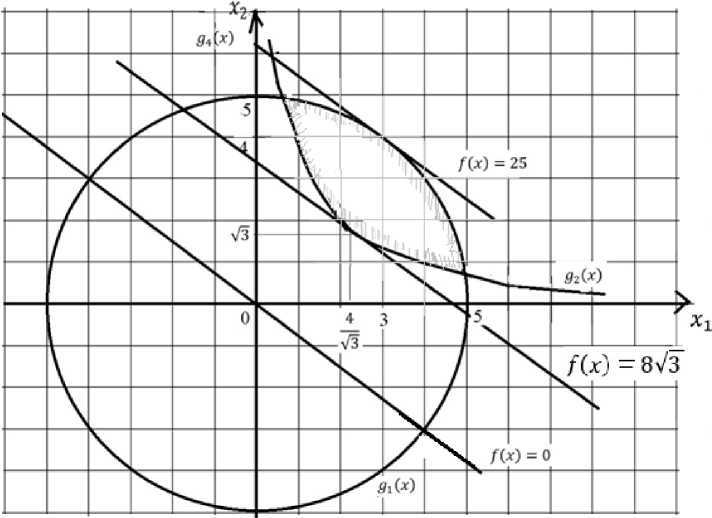
9зМ

Рисунок.

Точка максимума определяется из уравнения касательной к окружности с угловым коэффициентом к = — 3 / 4 : х 1 = 3 ; х 2 = 4 ; f_max = 25 . Точка минимума определяется из уравнения касательной к гиперболе с тем же угловым к оэффицие н том к = — 3 / 4 : х 1 = 4 V 3 / 3 ; х 2 = V 3 ; f min = 8 V 3 .

Решим теперь задачу аналитически. Составим обобщенную функцию Лагранжа

L(х,Л 0 ,Л) = Л 0 ( 3 х 1 + 4 х2 )

+ Л1 (х2 + х 2 — 25)

+ Л 2 (4 — х 1х 2 ) + Л 3 (—х 1) + Л 4 (—х 2 ).

Рассмотрим два случая: Л0 = 0 и Л0 * 0. Так как задача уже была решена графически, то рисунок показывает в любой экстремальной точке только одно активное ограничение, градиент которого ^д^(х*) * 0 ,j = 1, 2. Это говорит об отсутствии нерегулярной стационарной точки, т.е. остается рассмотреть случай

Л о * 0 . Запишем необходимые условия экстремума 1-го порядка.

L'X]= 3 + 2 х 1Л 1 — х 2Л 2 — Л 3 = 0;

Ь'Х2 = 4 + 2 х 2Л 1 — х 1Л 2 — Л 4 = 0;

х2 + х2 < 25; х 1х2 > 4; х 1 > 0;х2 > 0;

Лj > 0,j = 1,4 min и Лj < 0,j = 1,4 тах

Л1 (х2 + х2 — 25) = 0; Л2 (4 — х 1х2) = 0; Л3 (—х 1) = 0; Л4 (—х2) = 0.

Последние 4 уравнения позволяют рассмотреть 2⁴ варианта решений, из которых только два приводят к положительному результату, остальные 14 вариантов дают

противоречивые значения множителей Лагранжа или несовместность всей системы. Рассмотрим их подробно:

• а) Л 1 * 0,Л2 = Л3 = Л4 = 0 ^ 3 + 2х 1 Л 1 = 0; 4 + 2х2Л 1 = 0; х2 + х2 = 25 ^

х 1 = 3; х 2 = 4; Л 1 = — 1 / 2.

В этой точке выполняются достаточные условия 1-го порядка, а точка соответствует локальному максимуму;

• б) Л 2 Ф 0 , Л 1 = Л з = Л 4 = 0 ^ 3 — х 2 Л 2 = 0; 4 — х 1 А 2 = 0;х 1 х 2 = 4 ^

• ⁴ ^3             к

х 1 = —^—; х 2 = V 3; Л 2 = V 3 .

В этой точке выполняются достаточные условия 1 -го порядка, а точка соответствует локальному минимуму.

Проверим достаточные условия 1-го порядка. В обеих точках активным являет-

ся только одно ограничение, поэтому до статочные условия 1-го порядка не выпол няются. Проверим достаточные условия 2 го порядка.

d ² L = 2 Л 1 (dх 2 + dх 2 ) — 2 Л ₂ dх ₁dх ₂ .

d2L(3; 4) = —dх2 — dх2 < 0 ^ тах d2L(4V3/3; V3) = — 2V3dх 1 dх2 = 8V3 dх2 > 0 ^ min

Остаётся вычислить значения функции: f_max = f(3 ; 4 ) = 25 ;

( 4 V Л f min = f(—;V )

= 8 V .

Пример 3. Найти экстремум функции f(х) = х 1 х₂ при условии д 1 (х) = 4х ² + х 2 — 4 = 0 и д₂ (х) = х ² + 2х 2 — 8 < 0 .

Решение. Составим обобщенную функцию Лагранжа

L(х,Л 0 ,Л) = Л 0 х 1 х ₂ + Л 1 ( 4 х ² + х 2 — 4) + Л ₂ (х ² + 2 х 2 — 8)

Выпишем необходимые условия экстремума 1-го порядка

• LX] = Л 0 х 2 + 8 х 1 Л 1 + 2 х 1 Л 2 =

LX2 = Л 0 х 1 + 2 х 2 Л1 + 4 х 2 Л 2 =

4 х2 + х 2 — 4 = 0; х2 + 2 х 2 — 8

Л2 > 0, min и Л2 < 0, тах

Л 2 (х ² + 2 х 2 — 8) = 0.

Пусть Л0 = 0 ^    8х 1 Л 1 + 2х 1 Л2 = 0; 2х2 Л 1 + 4х2 Л2

4х ² + х2 — 4 = 0; Л 2 (х ² + 2х2 — 8) = 0.

• а)    Л₂ = 0 ^ х 1 Л 1 = 0 ; х₂Л 1 = 0; 4х ² + х 2 — 4 = 0. Возможны два варианта: Л 1 = 0, что противоречит условию не равенства нулю всех множителей одновременно; Л 1 Ф 0 ^ х 1 = х₂ = 0, а система ограничений несовместна;

• б)    Л₂ Ф 0 ^          х 1 (4Л 1 + Л₂) = 0 ; х₂ (Л 1 + 2Л₂) = 0 ;

4 х 2 + х 2 — 4 = 0; х 2 + 2 х 2 — 8 = 0.

Здесь также возможны два варианта:

• 1)    x 1 = 0; x 2 = 4 ; Л 1 = — 2Л₂ ; и две нерегулярные точки (0; 2) и (0; -2), а Л ₂ не ограничено знаком;

• 2)    4Л 1 + Л₂ = 0 ; x ₂ (Л 1 + 2Л₂) = 0 ; 4x ² + x 2 — 4 = 0 ; x ² + 2x 2 — 8 = 0 ;  система несов

местна.

Пусть Л 0 ^ 0 ^ x2 + 8x 1Л1 + 2x 1 Л2 = 0; x 1 + 2x2 Л 1 + 4x2 Л2 =

4 x2 + x 2 — 4 = 0;       Л 2 (x2 + 2 x2 — 8)=

• а)    Л ₂ = 0 ^ x₂ + 8x 1 Л 1 = 0 ; x 1 + 2x₂Л 1 = 0 ; 4x ² + x 2 — 4 = 0 . Откуда имеем четыре ре

гулярные точки:

(72; 72); (7г2; —V2); (—72; 72); (—12; —V2) и Л1 = —5

• б)    Л2 Ф 0 ^ x2 + 8x 1 Л 1 + 2x 1 Л2 = 0; x 1 + 2x2Л 1 + 4x2Л2=

4 x ² + x 2 — 4 = 0 ; x ² + 2 x 2 — 8 = 0 .

Данная система несовместна.

Проверим достаточные условия 1-го порядка. Эти условия для нерегулярных точек проверять не надо. Для регулярных точек ограничение неравенство является пассивным, поэтому следует проверить необходимые условия 2-го порядка.

д 2 L  _ dx 1dx 2   1’

d-LL = 8Л,+ 2Л2; d-LL = 2Л, + 4Л2;

dx 2     ^{1     2} dx 2     ^{1     2}

d ² L = ( 8 Л 1 + 2 Л ₂ )dx 2 + (2 Л 1 + 4 Л ₂ )dx 2 + 2 dx 1 dx ₂.

Из 4x ² + x 2 — 4 = 0 получим dx₂ =

— dx₂. С учетом Л₂ = — — второй дифференци- х 2                               2 X 2

ал примет вид d2L(—T2 ; —^)

d ² L = (— X )( 16dx ² + 2dx 2 ). Для исследуемых точек: d ² l( 1 ; 72) =

< 0 ^ локальный max;

d ² L (— ¹ ; 72) = d ² L ( ¹ ; —72) >

0 ^ локальный min.

Достаточные условия 2-го порядка также выполняются.

Остается вычислить значение функции во всех найденных точках:

f ( 1 ; 72)=f(— 1 ; —72 ) = 1 = f max

f( 1=; —72 ) =f(— 2=; 72 ) = — 1 =f_mtn

f(0; 2 ) = f(0; — 2) = 0 не является точкой экстремума.

Заключение

В заключении можно сделать следующие выводы о решении задачи нелинейной оптимизации:

• -    если удается доказать регулярность допустимой области, достаточно рассмотреть классическую функцию Лагранжа;

• -    если условия регулярности не выполняются или доказать их проблематично,

необходимо обязательно рассмотреть обобщенную функцию Лагранжа;

• -    помимо необходимых и достаточных условий экстремума 1-го порядка при их невыполнении следует проверить необходимые и достаточные условия 2-го порядка;

• -    если не удаётся найти решение задачи аналитически, необходимо воспользоваться подходящими численными методами.