Некоторые проявления неравенства Леви
Автор: Исмаилов Н.Т., Бахрамов Р.К.
Журнал: Мировая наука @science-j
Рубрика: Основной раздел
Статья в выпуске: 2 (83), 2024 года.
Бесплатный доступ
Для случая d>1 исследованы неравенства Леви, упомянутые в теоремах статьи, а также неравенства, упомянутые в научных исследованиях О.И.Клёсова, А.Н.Колмогорова и П.Леви.
Медиана случайной величины, лемма гуту, некоррелированные случайные величины, законе повторных логарифмов
Короткий адрес: https://sciup.org/140304034
IDR: 140304034
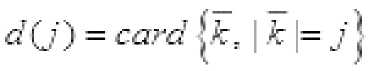
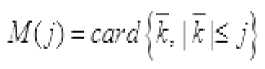
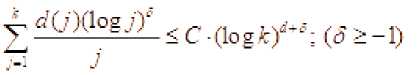
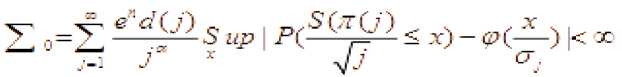
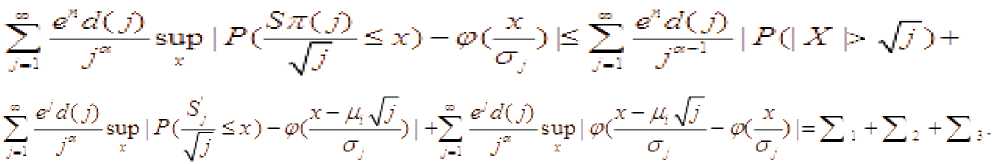
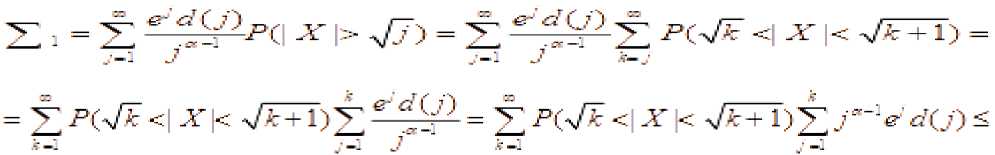
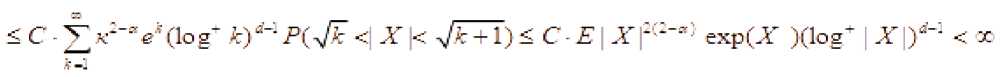
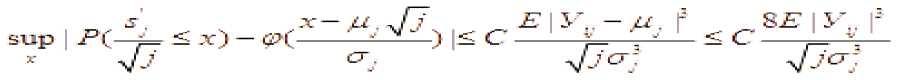
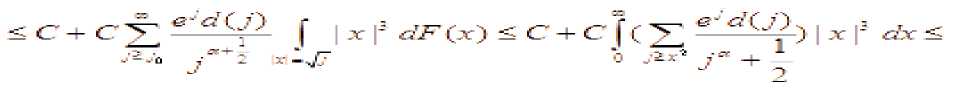
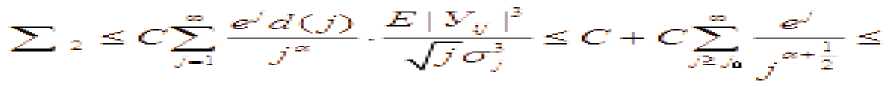
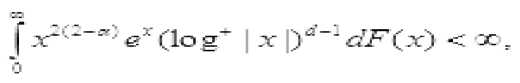
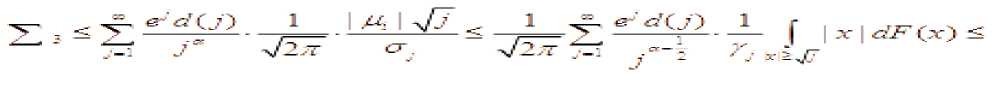
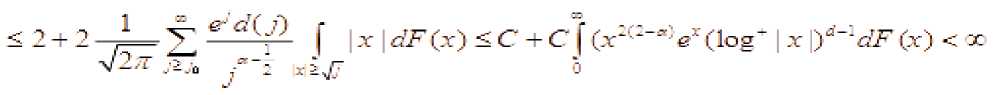
Список литературы Некоторые проявления неравенства Леви
- Королюк В.C. Граничные задачи для сложных пуассоновских процессов. Киев, Наукова думка, 1975.
- Братийчук В.С. Гусак Д.В. Граничные задачи для процессов с независимыми приращениями. Киев, Наукова думка,1990.
- Лотов В.И. О достижении высокого уровня блужданием с задержкой внуле. Сибирский матем. журн,1999, том 40, номер 6, cтр.1276-1288.
- Барон М. И. О моменте первого достижения для процессов ожидания. Теория вероят. и ее примен. 1996, Том 41, выпуск 2, стр. 396-403.
- Khоdjibayev V.R. Asymptotic representations for characteristics of exit from an interval for stochastic processes with independent increments. Siberian Adv. Math,1997, T. 7, №3, pp.75-86.
Статья научная
