Некоторые теоретические стороны расчета температурных деформаций подземных бесканальных теплопроводов

В настоящее время наиболее корректный и точный расчет трубопроводов тепловых сетей, засыпанных грунтом, на компенсацию температурных деформаций является актуальной задачей. Это обусловлено тем, что при подземной бесканальной прокладке теплосети происходит существенная экономия капиталовложений, но расчет защемленного в грунте теплопровода имеет собственную специфику, которая не позволяет применять те же расчетные алгоритмы, как в случае расчета надземного или канального теплопровода. Специализированной компьютерной программы может и не быть у инженера в наличии, а использование номограмм сейчас можно считать очень некорректным решением. Правильная расстановка компенсационных устройств и неподвижных опор в бесканальном теплопроводе позволяет экономить капиталовложения и гарантировать надежность теплотрассы. Можно обойтись минимальным количеством неподвижных опор и компенсационных устройств. Для этого необходимо понимать физику процесса температурных деформаций бесканальных теплопроводов.

В России исследования по теоретической и опытной части работы бесканальных теплопроводов были проведены первые в 1951-1952 гг. работниками управления теплосети «Ленэнерго» при содействии сотрудников кафедры теплогазоснабжения Ленинградского инженерного института на действующих теплосетях г. Ленинграда.

Теоретическая модель расчета температурных деформаций подземных бесканальных теплопроводов

В бесканальных теплопроводах при проведении расчетов на прочность и компенсацию температурных деформаций необходимо учитывать действия больших осевых усилий и напряжений, вызванных силами трения в грунте, и ограничением или отсутствием поперечных перемещений зажатых окружающим грунтом теплопроводов с монолитными теплоизоляционными оболочками. В таких теплопроводах рассматриваются зоны скольжения (компенсации), – 547 – в которых компенсация температурных деформаций осуществляется за счет линейных и угловых перемещений; зоны неподвижности (защемления), в которых компенсация температурных деформаций осуществляется за счет изменения осевого напряжения; зоны изгиба, примыкающие непосредственно к компенсаторам и перемещающиеся при нагреве в осевом и боковом направлениях.

Рассмотрим теоретическую модель участка бесканального теплопровода. Поставим следующие условия: концы теплопровода свободны и могут перемещаться в осевом направлении; сила трения грунта распределена с одинаковой интенсивностью по длине теплопровода; температура по длине трубопровода постоянна; при изменении температуры осевые перемещения теплопровода распространяются от компенсаторов у концов участка к его середине. Пусть lk – перемещающийся участок, L – половина длины участка теплопровода. Перепад температур, при котором lk = L, назовем предельным температурным перепадом и обозначим Δtпр. При lk = L температурное напряжение для сечения в середине участка теплопровода будет определяться по уравнению где σt – температурное напряжение; α – коэффициент линейного расширения материала теплопровода; E – модуль упругости материала теплопровода; P – сила трения, отнесенная к единице длины трубы; F – площадь поперечного сечения трубы.

На рис. 1 температурные перемещения распространяются не на всю длину участка теплопровода, так как l_k <  L . В точках B и C напряжения равны. Уравнение для определения температурного напряжения в этом случае будет иметь вид

Р1

a_t = aE^t =                                                     (2)

F где Δt – температурный перепад.

Выведем из уравнения (1) зависимость для определения предельного температурного пе- репада

At op =

2L. aEF

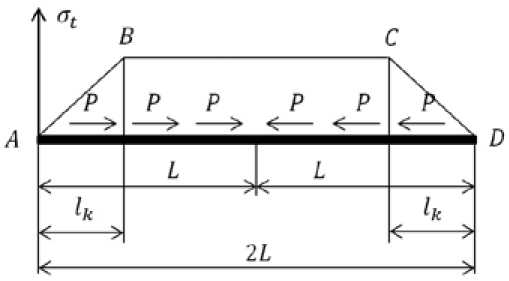
Рис. 1. Распределение температурного напряжения по длине участка теплопровода при температурном перепаде ниже предельного

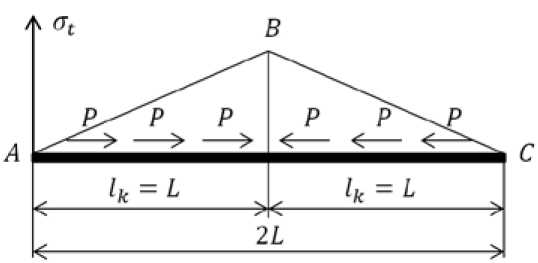
Рис. 2. Распределение температурного напряжения по длине участка теплопровода при предельном температурном перепаде

На рис. 2 в середине участка теплопровода в точке B температурные напряжения максимальны. Если концы теплопровода в точках A и C остаются свободными, то при дальнейшем увеличении температурного перепада возрастания температурного напряжения не происходит. Дальнейшие перемещения концов теплопровода идут пропорционально температурному перепаду. Если же в концевых точках установлены неподвижные опоры, то при возрастании температурного перепада напряжения будут непрерывно увеличиваться до потери устойчивости участка от продольного изгиба.

Определим перемещение конца теплопровода при отсутствии силы упругого отпора компенсатора. Перемещение конца теплопровода представляет собой сумму элементарных перемещений на длине l k , исходя из этого, можно записать следующее уравнение:

ik

f ardx аДк

''     \    ,         <,■                                                                               (4)

о

Преобразуя σt согласно уравнению (2), можно переписать уравнение (4) следующим об- разом:

PhL

2EF '

С учетом вышеприведенных уравнений можно записать такую зависимость для определения l k :

aE^tF ^к = р

5E a^t'

Для предельного состояния A t в уравнении (6) следует заменить на A t_np . Из уравнения (4) вытекает, что в предельном состоянии, когда l k = L , для теплопроводов защемленных грунтом удлинение δ _пр будет определяться как

5 пр =

atL

2:

aMnpL

Для теплопроводов, не защемленных грунтом и уложенных на опорах без трения при таком же температурном перепаде, уравнение (7) перепишется в виде

м

а)

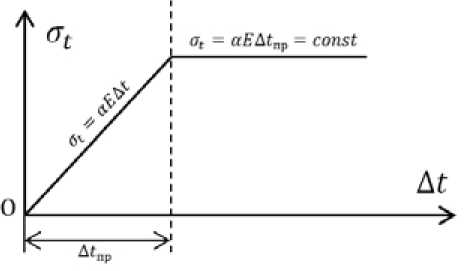
Рис. 3. Зависимость перемещений концов теплопровода и температурных напряжений от температурного перепада

б)

5пр aAtnpL.                                                                 (8)

Таким образом, температурные удлинения теплопровода, защемленного грунтом, при предельном температурном перепаде в два раза меньше величины удлинения полностью свободного теплопровода такой же длины. Этим объясняется недокомпенсация температурных деформаций бесканальных теплопроводов.

На рис. 3 а представлены две зависимости перемещений концов теплопровода от изменения его температуры. Зависимость 1 характеризует свободный теплопровод, не встречающий сопротивления сил трения грунта. Зависимость 2 характеризует бесканальный теплопровод.

Для зависимости 1 (рис. 3 а ) перемещения пропорциональны температурному перепаду Δ t , и зависимость представляет собой прямую линию ОА2 . Зависимость 2 на отрезке ОВ – кривая линия, в точке В переходящая в прямую. При Δ t > Δ t пр температурные перемещения пропорциональны Δ t и прямая ВВ2 параллельна прямой АА2 . Согласно уравнениям (7), (8) при Δ t = Δ t_пр отрезок СВ равен половине отрезка СА .

На рис. 3б представлена зависимость температурного напряжения σt в бесканальном теплопроводе от температурного перепада Δt. В точке, которая соответствует предельному тем-– 550 – пературному перепаду Δtпр, температурные напряжения достигают максимально возможной величины, определяемой из уравнения (1). При дальнейшем увеличении температурного пере- пада напряжение остается постоянным.

Рассмотрим на основе графика на рис. 3 а явление недокомпенсации температурных деформаций бесканальных теплопроводов. При начальном периоде нагрева теплопровода, когда C1S1

A t < A t „„ , недокомпенсация больше 50 %, так как на графике < 0,5. При A t = A t_np недоком- СВ                                 L ¹ ^ ¹

пенсация равна 50 %, так как — = 0,5. При A t 2 > 2A t_np недокомпенсация будет уменьшаться,

С2В2

так как---= 0,75. Таким образом, измеряя перемещения концов теплопровода A l_t , при ма- С2Л2

лых величинах температурного перепада Δt получим преувеличенную недокомпенсацию, а при больших значениях Δ – преуменьшенную. Исходя из этого, коэффициент недокомпенсации не может рассматриваться в качестве критерия, характеризующего степень защемления труб грунтом.

Максимальное удлинение зоны компенсации Δ l_t на участке от свободного конца до зоны защемления (величина l k на рис. 1, 2) из-за изменения температурного перепада с учетом противодействия сил трения будет определяться по уравнению

р;к2

Mt - к«м - -^

Если измерены Δ l_t и Δ t , то можно вычислить интенсивность сил трения грунта:

р =

2EF

аМ

Mt ^к •

Теоретически силы трения в грунте могут быть определены из следующего уравнения:

P = pHKDnntgV,                                                (11)

где ρ – объемный вес 1 грунта; H – заглубление до верха теплоизоляционной конструкции теплопровода; D – наружный диаметр теплоизоляции (для изоляции, в которой перемещения n теплопровода происходят внутри оболочки, Dn равен наружному диаметру трубы); n – коэффициент перегрузки; φ – угол внутреннего трения грунта.

Формула (11) справедлива для труб малого и среднего диаметров, для которых интенсивность вертикального давления грунта pH равна горизонтальному (боковому) давлению q . Для теплопроводов с диаметром более 250 мм следует учитывать неравенство этих давлений. В этом случае сила трения в грунте будет определяться следующим образом:

Р

^РН2 ^ nDnntgy.

Интенсивность горизонтального (бокового) давления будет определяться из уравнения

q = р уН + -2^j tg2(45 - ф^2) .

Следует отметить, что наиболее точное значение силы трения в грунте возможно получить только путем непосредственного измерения на действующих теплопроводах.

Рассмотрим распределение осевых сжимающих сил трения в бесканальных теплопроводах с П-образными компенсаторами в компенсаторных нишах при различных схемах расчетных участков. Температурное напряжение σ _t возле неподвижной опоры или зоны защемления грунтом с учетом уравнений (1), (2) находим так:

= ^к + ^

t F F - где Pk – реакция упругого отпора компенсатора.

Реакцию упругого отпора гибких радиальных компенсаторов из труб (согласно СП 41-1052002 компенсирующие устройства группы 1а) вычисляем как

p‘ - у+p ■ - где Px, Py – векторы сил упругой деформации относительно координатных осей X и Y соответственно.

Силы упругой деформации относительно координатных осей:

p _ ^^/yO + ^У]хуО p Jx°yO JyO0 (16) _ ky]x0 + ^Xjxy0 ^y =              2 htJ , JxOJyO JxyO (17) где Δx, Δy – расчетные температурные расширения компенсатора в направлении осей x и y соответственно; Et – модуль упругости материала трубы при расчетной температуре; J – момент инерции поперечного сечения стенки трубы, определяемый по формуле

/ = ^[On4 — (Dn — 2s)4],

где Dn – наружный диаметр трубопровода; s – толщина стенки трубы; J_{x 0}, J_{y 0} – центральные моменты инерции приведенной длины осевой линии компенсатора, которые определяются следующим образом:

f dl _ f dl LiV К V Jk'

f э dl D f dl Их2к-^Ь где x, y – координаты рассматриваемого сечения компенсатора в заданной системе координат; x0, y0 – координаты упругого центра тяжести гибкого радиального компенсатора; K – коэффициент гибкости элемента компенсатора (для прямой трубы K=1); l – длина рассматриваемого элемента компенсатора (прямая труба или отвод); Jxy0 – центральный центробежный момент инерции приведенной длины осевой линии компенсатора, который можно найти по формуле fxydl f dl

1 у xv 1

J xyO

Координаты упругого центра тяжести гибкого радиального компенсатора вычисляют по формулам

% o

^{У о}

J*K Sy

Г dl    Lp’

J К

r dl Jy-K_sx

f dl L’

^K   p

где S x , S y – статические моменты инерции приведенной длины осевой лини компенсатора относительно осей x и y соответственно; L_p – приведенная длина осевой линии компенсатора.

Приведенную длину осевой линии компенсатора определяют по формуле

‘₽=2'+257^^«'

где Σ l – сумма длин прямых труб компенсатора; φ – угол отвода в градусах; K – коэффициент гибкости отвода; R - радиус отвода; ^ ^^ KR - сумма приведенных длин отводов компенсатора.

Коэффициент гибкости отвода можно рассчитать согласно РД 10-400-01 или другим способом.

Изобразим графически распределение температурных напряжений для различных схем подземных бесканальных участков теплопроводов с П-образными компенсаторами в компенсаторных нишах.

На рис. 4 даны эпюры температурных напряжений для двух конфигураций подземных бесканальных участков теплопроводов с П-образными компенсаторами в компенсаторных нишах. На участках установлены неподвижные опоры. Максимальные напряжения возникают в местах примыкания теплопровода к неподвижным опорам и равны для представленных конфигураций участков. Зона перемещения теплопровода l k равна длине участка L для двух представленных схем, отсюда следует, что температурный перепад больше предельного или равен ему Δ t ≥ Δ t пр .

Рассмотрим теперь случай, когда l_k <  L и теплопровод частично зажат грунтом.

На рис. 5 изображены эпюры температурных напряжений для конфигураций с односторонними и двухсторонними П-образными компенсаторами. В обоих случаях зона перемещения меньше расстояния между неподвижными опорами l k <  L . Отсюда следует, что температурный перепад меньше, чем предельный: Δ t < Δ t_пр .

Рассмотрим теперь схему с П-образным компенсатором, расположенным в середине участка теплопровода.

На рис. 6 видно, что при установке компенсатора в середине участка температурные напряжения уменьшаются по сравнению с остальными рассмотренными схемами. Такая схема установки получила название схемы с «плавающими» компенсаторами и была предложена в – 553 –

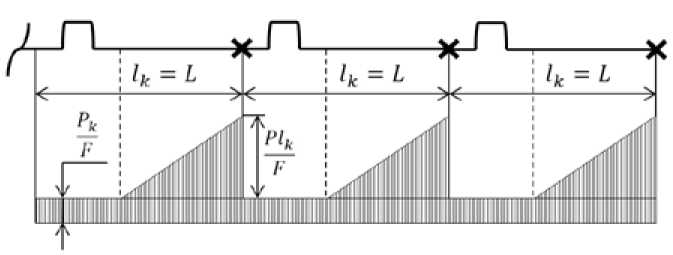
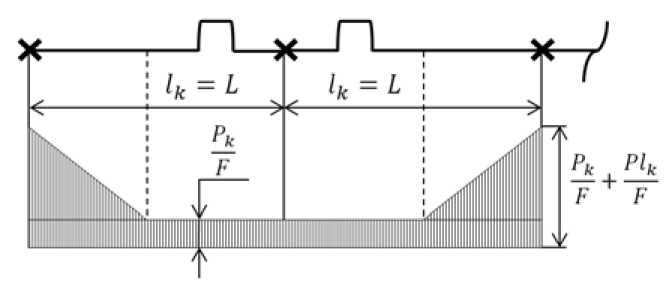
Рис. 4. Температурные напряжения в бесканальном теплопроводе: а – с односторонними П-образными компенсаторами; б – с двухсторонними П-образными компенсаторами

свое время сотрудниками Ленинградского филиала института «Теплоэлектропроект». Схема с плавающими компенсаторами более экономична, так как позволяет в 2 раза увеличить длину участков и обойтись меньшим числом компенсаторов.

Рассмотрим теперь случай установки плавающих компенсаторов на участках с неравными длинами и при Δ t < Δ t пр .

На рис. 7 видно, что L 1 >  L 2 и l k >  L 2 /2. Напряжения на участке L 1 меньше максимального, так как l <  L /2. По мере увеличения Δ t напряжения на участке L достигнут максимального

PL значения - и на неподвижную опору между участками L1 и L2 будет передаваться неуравно-2F вешенное усилие Pt, равное разности двух усилий и определяемое уравнением

P t

PL ,

^^^^^^^^

pl2

-^

- L2) ■

Компенсация температурных деформаций, рассмотренных на рис. 4–7 схем участков теплопроводов, осуществлялась при помощи гибких П-образных компенсаторов. В современных конструкциях тепловых сетей используются стартовые и осевые сильфонные компенсаторы. Изучим более подробно случай применения стартовых компенсаторов. Стартовые компенсаторы осуществляют растяжку теплопровода, защемленного в грунте. При их применении теплопровод становится неразрезной конструкцией, так как эти компенсаторы срабатывают только – 554 –

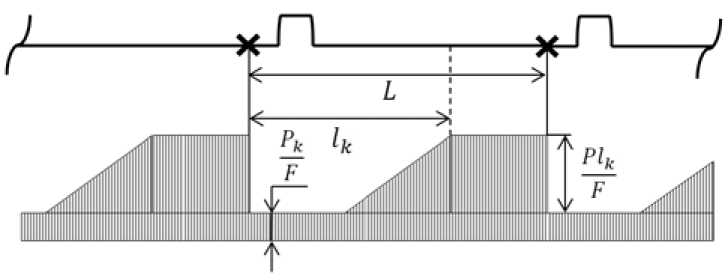
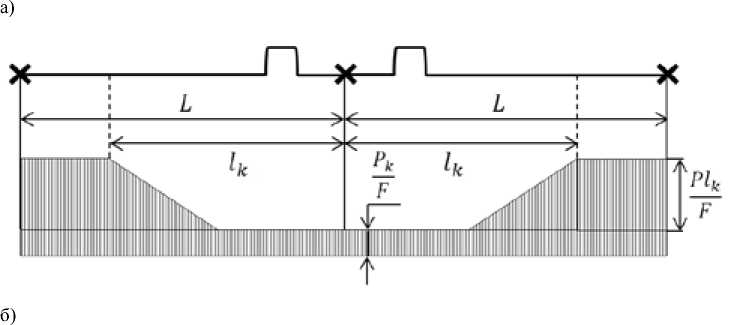
Рис. 5. Температурные напряжения в бесканальном теплопроводе с зонами защемления грунтом: а – с односторонними П-образными компенсаторами; б – с двухсторонними П-образными компенсаторами

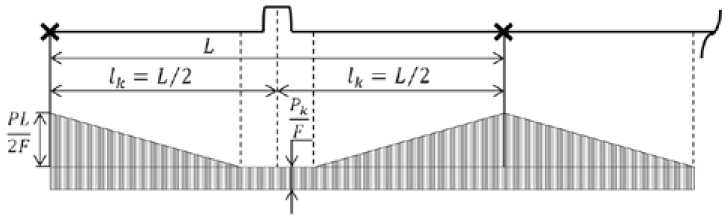
Рис. 6. Температурные напряжения в бесканальном теплопроводе с П-образным компенсатором в середине участка один раз, после растяжки теплопровода, после чего завариваются. Растяжка осуществляется путем предварительного прогрева теплопровода до температуры замыкания. Стартовые компенсаторы позволяют прокладывать теплопроводы в виде длинных прямых участков, на которых температурные деформации компенсируются осевыми напряжениями растяжения-сжатия самого теплопровода. Размах температурного напряжения Δσ при переходе теплопровода со стартовыми компенсаторами из холодного состояния в рабочее и обратно определяется по формуле

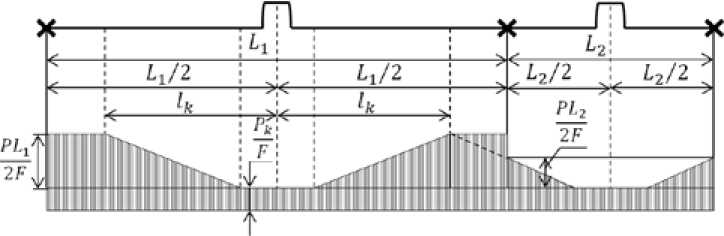
Рис. 7. Температурные напряжения в бесканальном теплопроводе для двух участков разных длин с П-образным компенсатором в середине

Дст — а(Т_т Т^Е ,                                                 (2⁶⁾

где α – коэффициент линейных температурных расширений; Tr – температура теплопровода в рабочем состоянии; T – температура теплопровода в холодном состоянии; E – модуль упруго-h сти материала теплопровода.

Размах температурных напряжений является частью диапазона допускаемых напряжений 2σ доп , равного удвоенному допускаемому напряжению. Оставшаяся часть диапазона приходится на обеспечение сил трения скольжения трубопровода о грунт, возникающих в процессе термического натяжения и продолжающих действовать некоторое время после его окончания в виде сил трения покоя σ_тр. Для предельного состояния можно записать следующее равенство:

² ° доп = Ду + ^у тр .                                                     ⁽²⁷⁾

Максимальное расстояние прямого участка от стартового компенсатора до неподвижной опоры или зоны защемления можно определить по формуле

Л   = ^тр                                              (28)

Ч тр '

где F ст – площадь поперечного сечения стенки трубы; q тр – сила трения, приходящаяся на единицу длины трассы.

Стартовый компенсатор примыкает к двум участкам, каждый из которых равен расстоянию от компенсатора до неподвижной опоры или зоны защемления. Таким образом, расстояние между стартовыми компенсаторами будет определяться как 2 L max .

Силу трения q _тр, приходящуюся на единицу длины трассы, можно вычислить по формуле

. . = д[(1 - O,5sin^_r p )y_r p Z^D_o + у],                                 (29)

где μ – коэффициент трения трубной оболочки о грунт; φ_гр – угол внутреннего трения грунта; γ гр – объемный вес грунта; Z – глубина заложения теплопровода; D 0 – наружный диаметр кожуха изоляции; д - вес теплопровода с изоляцией и теплоносителем, приходящийся на единицу его длины.

Если стартовые компенсаторы ставятся на разном расстоянии друг от друга, то осевые напряжения могут возрасти по сравнению с результатами расчета по вышеприведенным формулам.

Температуру замыкания Tz стартовых компенсаторов найдем по формуле т = 1 z

Tr-

Температура замыкания, вычисленная по формуле (30), позволяет обеспечить одинаковый температурный перепад при охлаждении и нагреве теплопровода.

Величину сжатия δ стартового компенсатора в момент замыкания определяем по формуле

:   ;'. у у ,;_";-;4,                                  (31)

2ЫСТ где Tm – температура монтажа (рекомендуется принимать среднюю температуру стенок теплопровода непосредственно перед началом термического натяжения).

Коэффициент 2 в формуле (31) указывает на то, что стартовый компенсатор примыкает к двум участкам теплопровода, длиной L max .

Протяженные участки бесканальных теплопроводов следует проверять по условию сохранения устойчивости труб на продольный изгиб. Кроме этого, расчеты на устойчивость необходимы при проектировании бескомпенсаторных теплопроводов, в первую очередь для обратных труб. Устойчивость бесканальных теплопроводов существенно выше, чем надземных или канальных теплопроводов, за счет сил противодействия грунта. Критическое усилие P кр , при котором неразрезной теплопровод теряет устойчивость, можно определить по формуле

1,1W2 кр = Е/       ,

где N – осевое сжимающее усилие в трубе; E – модуль упругости материала трубы; J – момент инерции поперечного сечения стенки трубы; i – начальный изгиб трубы, определяемый по формуле

к

200 ’ где Li – длина местного изгиба теплопровода, вычисляемая по формуле

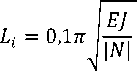
где | N | – абсолютное значение величины осевого сжимающего усилия в трубе.

Вертикальную нагрузку R_st , оказывающая стабилизирующее влияние устанавливают по формуле

R_st = q₈ r + Q tr + 2S sd ,                                               (35)

где q_gT - вес грунта над теплопроводом; q_tr - вес 1 м теплопровода с водой; S sd - сдвигающая сила, возникающая в результате давления грунта в состоянии покоя, определяемая по формуле

S_S d = 0,5¥2 ² К₀1дф гр ,                                                ⁽³⁶⁾

где γ – удельный вес грунта; Z – глубина засыпки по отношению к оси трубы; K ₀ – коэффициент давления грунта в состоянии покоя ( K 0 = 0,5); φ гр – угол внутреннего трения грунта.

Формула (36) справедлива, когда уровень стояния грунтовых вод ниже глубины заложения теплопровода. Вес грунта над теплопроводом можно вычислить по формуле q^U^.                (37)

где D 0 – наружный диаметр оболочки.

Осевое сжимающее усилие в защемленном грунтом прямом участке теплопровода с равномерно распределенной вертикальной нагрузкой можно найти по формуле

N = -\_F_St(EaM-0,3a_rQSt) + PF_pl\,                              (38)

где Fst – площадь кольцевого сечения трубы; E – модуль упругости материала теплопровода; α – коэффициент линейного температурного расширения трубы; Δt – температурный перепад; σrast – растягивающее окружное напряжение от внутреннего давления; P – внутреннее давление; F – площадь действия внутреннего давления, определяемая p по формуле

^F _?ⁱ = 0,785О_ВН²,                                                         ⁽³⁹⁾

где D EH – внутренний диаметр теплопровода.

Рассмотрим влияние толщины стенки и глубины заложения на максимальную длину прямого участка бесканального теплопровода. Под максимальной длиной L max понимается расстояние от неподвижной опоры или начала зоны защемления грунтом до компенсирующего устройства. Будем вычислять L max по следующей формуле:

L„„ = ^ ^ ^ 3t ,                                                     (40)

Чтр где σd – допускаемое осевое напряжение в трубе; Fst – площадь поперечного сечения стенки трубы; qтр – то же, что и в формуле (29).

Результаты исследования расчетных моделей бесканальных участков теплопроводов

В качестве примера рассмотрим теплопровод с трубой 159х4,5 мм, рабочей температурой 130 °С, рабочим давлением 1,6 МПа. Грунт песчаный, материал теплопровода сталь Вст3сп5, диаметр кожуха изоляции 250 мм, вес изоляции 159 Н/м, плотность теплоносителя 1000 кг/м3. Номинальное допускаемое напряжение для заданного материала при рассматриваемой темпе- ратуре составит 137 Н/мм2. Допускаемое осевое напряжение σd будем вычислять по следующей формуле:

ай = 1,25^t J1,04№ - 0,4[ст]Р [:

D bh

2(°вн +

—— + 11 , 5)5ф

где φ i – коэффициент прочности сварного шва при расчете на изгиб (примем 1); [σ] – номинальное допускаемое напряжение; P – избыточное внутреннее давление; D _EH – внутренний диаметр трубопровода; s – толщина стенки трубы; φ – коэффициент прочности сварного шва при расчете на давление (примем 0,8).

Представим результаты расчетов в форме графика (рис. 8)

На рис. 8 видно: 1) как увеличение толщины стенки трубы теплопровода позволяет увеличить максимальную длину участка; 2) как увеличение глубины засыпки грунтом уменьшает максимальную длину участка.

Рассмотрим влияние глубины засыпки теплопровода из вышеприведенного примера на стабилизирующую вертикальную нагрузку при толщине стенки теплопровода 4,5 мм. Представим результаты графически (рис. 9).

Построим аналогичный график для теплопровода с толщиной стенки 6 мм (рис. 10).

На рис. 9, 10 видно, что увеличение толщины стенки приводит только к увеличению критической нагрузки. Следует отметить, что для графиков на рис. 9, 10 не учитывался уровень грунтовых вод. Если уровень грунтовых вод выше глубины заложения теплопровода, то существует вероятность его всплытия. В таких случаях необходимо предусматривать вес балласта, который обеспечит теплопроводу надежную отрицательную плавучесть.

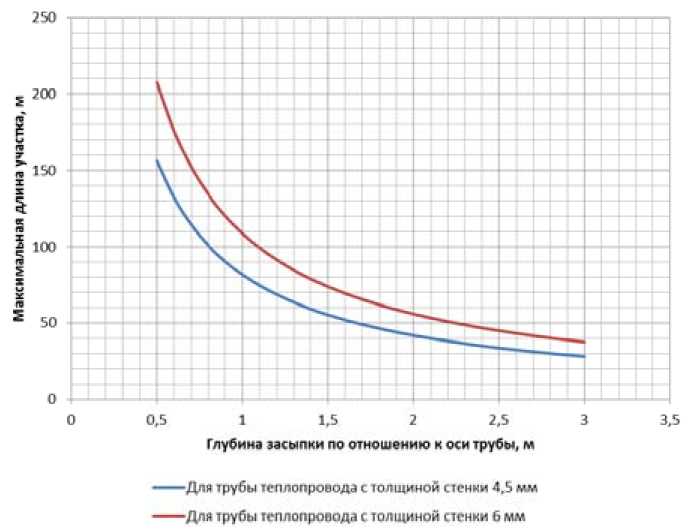
Рис. 8. Зависимость максимальной длины участка подземного теплопровода от глубины засыпки

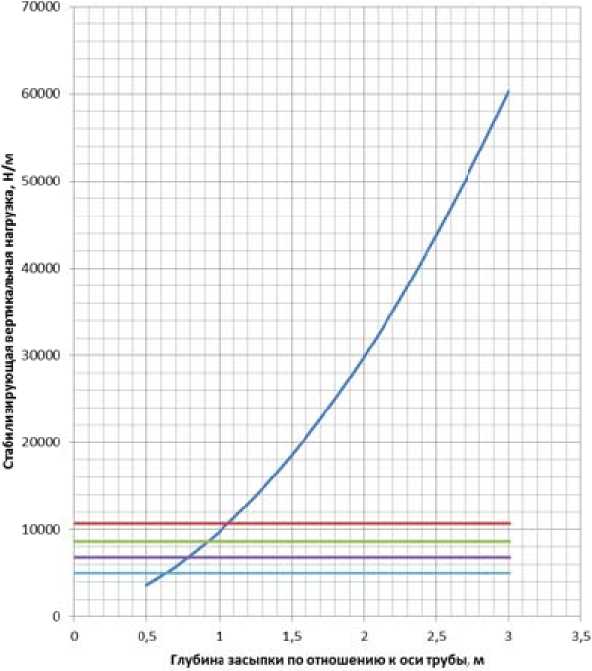
зависимость стабилизирующей нагрузки от глубины засыпки Критическое усилие при перепаде температур 150 градусов Критическое усилие при перепаде температур 130градусов Критическое усилие при перепаде температур ИОградусов Критическое усилие при перепаде температур 90 градусов

Рис. 9. Зависимость стабилизирующей вертикальной нагрузки от глубины засыпки для теплопровода с толщиной стенки 4,5 мм

Выводы

На основании вышеизложенного можно сформулировать следующие выводы по теории расчета температурных деформаций бесканальных участков теплопроводов.

В начале нагрева или охлаждения температурные перемещения возникают только на некоторой длине l k , непосредственно примыкающей к свободным концам.

Температурные перемещения распространяются к середине участка теплопровода при увеличении температурного перепада до тех пор, пока l k станет равной половине длины участка. Температурный перепад, при котором l_k равно половине длины участка, назван предельным температурным перепадом.

Дальнейшее увеличение температурного перепада не вызывает возрастания температурных напряжений в бесканальном теплопроводе, если его концы остаются свободными.

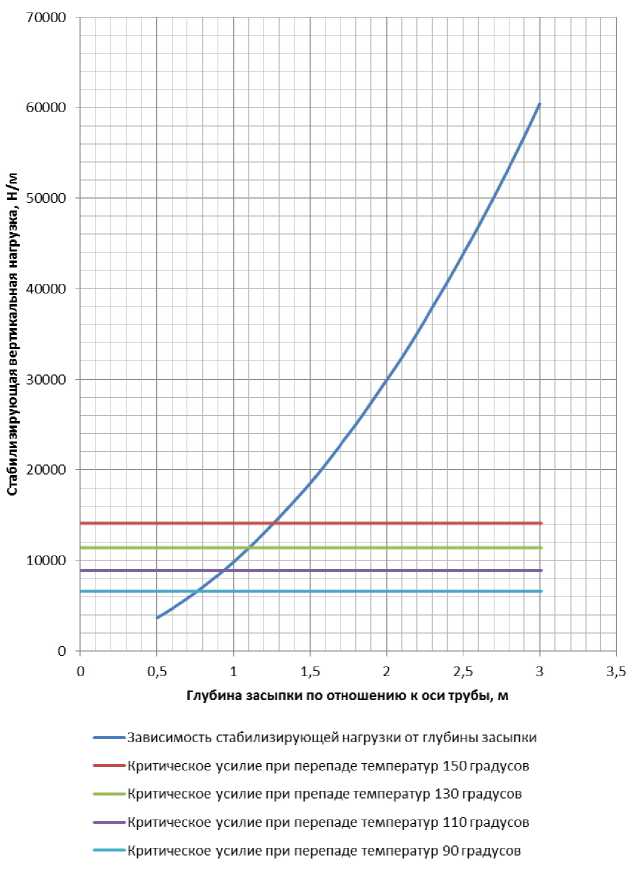
Рис. 10. Зависимость стабилизирующей вертикальной нагрузки от глубины засыпки для теплопровода с толщиной стенки 6 мм

Температурные удлинения теплопроводов в грунте составляют 50 % удлинений свободных теплопроводов такой же длины при условии Δ t = Δ t пр .

Коэффициент недокомпенсации температурных удлинений не пригоден в качестве критерия, характеризующего степень защемления труб грунтом, так как при малом температурном перепаде недокомпенсация преувеличивается, а при большом перепаде, наоборот, преуменьшается.

Достаточную характеристику, определяющую степень воздействия грунтовой среды на теплопровод, позволяет получить величина интенсивности сил трения грунта.

Середина участка теплопровода, имеющего на концах компенсаторы, остается неподвижной вне зависимости от того, установлена там неподвижная опора или нет.

Если неподвижная опора установлена несимметрично по отношению к компенсаторам, то значения l k и Δ t пр потребуют некоторой корректировки.

Самой выгодной с точки зрения экономии неподвижных опор является схема установки компенсатора в середине участка.

При проектировании бесканального теплопровода важен баланс между толщиной стенки, глубиной заложения и температурным перепадом.

Бесканальный теплопровод необходимо проверять на устойчивость.