Некоторые типы гипергеометрических лазерных пучков для оптического микроманипулирования

Недавно были рассмотрены новые световые моды – гипергеометрические (HyG) моды [1]. После этого появилось несколько обобщающих работ, в которых были рассмотрены гипергеометрические-гауссовые (HyGG) моды [2], HyG пучки [3] и круговые пучки (CiB) [4]. В [4] указано, что частными случаями круговых пучков являются многие известные световые пучки, например, стандартные [5] и элегантные [6] моды Лагерра-Гаусса (sLG, eLG), квадратичные Бессель-Гаусса (QBG) пучки [7]. Заметим, что HyG моды [1] и HyGG пучки [2] были реализованы с помощью жидкокристаллических микродисплеев.

В данной работе приводится явный вид лазерных пучков, которые являются частными случаями HyG пучков [3]. Это модифицированные квадратичные Бессель-Гаусс (mQBG) пучки, о которых упоминалось в [2], но не было приведено их явного вида, и которые отличаются от обычных QBG пучков [7]. Показано, что известные гауссовые оптические вихри (GOV) [8,9] являются также частным случаем HyG пучков. Получены явные аналитические выражения для новых световых пучков: полых гауссовых оптических вихрей (HGOV), модифицированных элегантных Лагерра-Гаусса (meLG) пучков и гамма-гипергеометрических ( у HyG) пучков. Эти световые пучки также являются частными случаями HyG пучков.

В работе приводятся экспериментальные результаты по формированию пары HyG пучков с номерами ( n , у ) и ( - n , -у ) с помощью бинарного дифракционного оптического элемента (ДОЭ). ДОЭ был синтезирован по технологии электронной микролитографии. Проведено сравнение экспериментальной и расчетной картин дифракции для HyG пучка. Приведены также результаты эксперимента по враще-

нию полистироловых шариков диаметром 5 мкм в световом кольце сформированного HyG пучка.

2. Общий вид HyG пучков

В [3] показано, что с помощью начального светового поля при z = 0 вида

E у ,n , m ( r , Ф , z = ⁰ ) =

2п

exp

r              I r I

--7 + i у In — + in ф

2o        V to J

где ( r , ф ) - полярные координаты в начальной

плоскости z = 0 , to и у - действительные параметры логарифмического аксикона, о - радиус перетяжки Гауссового пучка, n – номер сингулярности (целое число) спиральной фазовой пластинки (СФП), m – целое число – показатель степенной составляющей комплексной амплитуды, в произвольной плоскости z >  0 сформируется параксиальное световое поле, описываемое комплексной амплитудой вида:

^E у, n , m ^(р , ⁶ , z )

/ A n + 1 / V £7 V

(-i)    | z0 || V2о I

2nn! (zq2 JI toq J

n

I kop I I ikp      -1_fn + m + 2 + iу)

x exp —— + in6 Г ----------' x (2)

| V2 qz J     | 2 z J V 2 J

^x 1 F 1

n + m + 2 + i у

, n + 1,

2 kop | V2qz J

где z ₀ = k o ², q = ( 1 - iz ₀ / z ) 12 , ( p , 6 ) - полярные координаты в поперечной плоскости, Г ( x ) - гамма-функция, 1 F ( a , b , x ) - функция Куммера [10], k = 2 л/% - волновое число света, % - длина волны.

• 3.    Частные случаи HyG пучков

• 3.1.    Модифицированные квадратичные Бессель-Гаусса пучки

В этом разделе мы получим аналитические выражения для частных случаев HyG пучков: mQBG, GOV, HGOV, meLG и y HyG пучков.

Все эти пучки не являются модами свободного пространства и не сохраняют свою структуру при распространении. Дифракционная картина в сечении этих пучков представляет собой набор светлых и темных концентрических колец, среди которых самое яркое кольцо является основным, а остальные кольца – боковыми лепестками. Из этих пучков только mQBG пучки обладают бесконечной энергией, как, например, обычные моды Бесселя [11], а остальные пучки имеют конечную энергию.

Известна связь функции Куммера и функции Бесселя целого и полуцелого порядков [10]:

описываемым функцией J n ₂ ( ar ² ) exp ( - br ² + in ф ) , a и b - постоянные, а в любой другой плоскости z >  0 выражение для амплитуды QBG пучков можно получить с помощью справочного интеграла [13]:

^

J J_n ( ar ² ) exp ( - br ² ) J_n ( cr ) r d r =

1 _T        c² a                  c² b

₂ ( a ² _{+ b} ² ) 2 2 [ 4 ( a ² + b ²) J exp [ 4 ( a ² + b ²)

Пучки (4) порождаются с помощью другого светового поля в начальной плоскости:

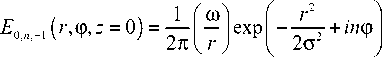
и [ n + 1

F ----, n + 1, x

¹ 1 2

1 n      I       I x

= Г — + 1 exp —

1 2     )     1 2

ix

n

n

ix

2 J

и поэтому отличаются от QBG пучков. Световые поля (4) можно назвать модифицированными квадратичными Бессель-Гаусс пучками (mQBG).

При а ^ ^ (гауссовый пучок заменяется плоской волной) из (4) получаются расходящиеся Бесселевы пучки, описанные в [3]:

где J _v ( x ) - функция Бесселя. Тогда из (2) с учетом (3) и при условии, что у = i ( m + 1 ) , получим:

E, _п    (р, 0, z ) =

г ( m + 1 ) , n , m \", , /

E ? 0, n , - 1 ⁽р , ⁰ , z ) = у        ^х

2 V 2n z

( л n + 1      [■ о ik Р ² 1 т [ к Р ²

х ( - i ) ² exp | in 0+--I J_n |----

^       4 z J 2 ^ 4 z

.

= E 0, n , - 1 ( р, ⁰ , z ) =

n + 1

( - г ) I kат 72л (2 zq

х exp

• _Q    ik Р ²         Р 2

in 0 +---— --——-

2 R 1 ( z ) 2а ( z )

х

х I

Р ² + ik Р 2 2а 2 ( z )    2 R ( z )

Световое поле (7) имеет особенность в центре начальной плоскости при z = 0 и r = 0 и обладает бесконечной энергией. Рассмотрим далее случаи без таких особенностей.

3.2. Гауссовы оптические вихри

В этом разделе приводится явный вид комплексной амплитуды для еще одного частного случая HyG пучков – GOV [8,9]. Известна рекуррентная связь между функциями Куммера [10]:

где

а ² ( z ) = 2 а ² | 1 + z I ,

I ^z 0 J

. ^{r (} _{Z )}= 2 _ . [i⁺i j ,

1 F ( a , b , - x ) = exp ( - x ) 1 F 1 ( b - a , b , x ) .            (9)

С учетом (9) общий вид HyG пучков дальнейшего удобно написать в виде:

(2) для

/ x           2z2 V

R ( z ) = R ( z ) | 1 +41 ,

I     ^z 0 J

, x ( - i ) n ^{+ 1}

^{F y} , ⁿ , ^{m (р} , ⁰ , ^z ) = 2 n n !

m + i y

I X

I _v ( x ) - модифицированная функция Бесселя.

Световые пучки, описываемые комплексной амплитудой (4), имеют сомножителями гауссовую экспоненту и функцию Бесселя. Поэтому они сходны с известными пучками Бесселя-Гаусса (BG) [12]. Зависимость аргумента функции Бесселя в (4) от радиальной координаты квадратичная, и поэтому пучки (4) сходны с QBG пучками [7]. Но QBG пучки порождаются начальным световым полем при z = 0 ,

n

I k ар I ^х f

( V2 qz J

■ „ ik Р ^{2 exp} in ^{0 +} ЧТ

хГ [ ^{n +} m ^{+ 2 +} i ^y I х

^х 1 ^F 1

n - m - i у

-

2 k ср I 72 qz J

_ I k ар |

, n + 1,

( V2 qz J

.

х

В [3] найдена связь между функцией Куммера и модифицированными функциями Бесселя:

n - 1

! F I n , n + 1, x | = Г I — 1 2 ² x

1 ¹ 1 2 I I 2 )

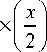
n - 1

^

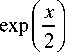
J exp ( - pr ² ) J_n ( cr ) d r =

In-1 ( x )- In+1 ( x )

Используя (11) и положив y= im , из общего вида (10) для HyG пучков можно получить частный случай в явной форме:

по параметру p :

^

J r ² exp ( - pr ² ) J_n ( cr ) d r =

,

n p 2

I c ² exp-- x

V 8 p J

^E im , n , m ( P , ⁶ , z ) = ^E 0, n ,0 ( P , ⁶ , z ) =

/ Л ^{n +1} A A _ A

( ^- 1 )       I z₀ II k op |

= r~ ^x I 2 I /— ^x

4V n   V zq JV V2 qz J

x

I 1 - n c ²1 I

V ~^- 8 p J n

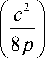
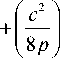
I

n - 2

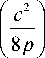
x exp in 6 +

ik p ²         p ²

2 R 1 ( z ) 2 o ² ( z )

x I n - 1 ( y ) - I n + 1 ( y )

где

y = 1 1 ^P 2

z

x

Сравнивая правые части (15) и (17), получим связь между функцией Куммера и модифицированными функциями Бесселя:

n

I ^{n + 3}                 I     ^-2

1 F 1 1    2 , n + 1, - x I = x ² exp

x I С

— V n n ! x

2 J

xr^{- 1}

| n + 3 1

V J

1 1 - n V ~

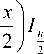
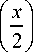
x

⁺ I n - 2

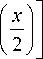
P ²        ik P ²

2 o ² ( z )    2 R ( z ) .

Используя (18), из общего уравнения (2), при ус ловии y= i (m -1), получим явное выражение для

Световое поле (12) порождается начальным полем вида:

новых световых пучков:

E 0, n ,0 ( r , Ф , z = ⁰ ) = J exp 2 n

Г2

— + inф |,(13)

2oJ

E., _n     (p, 6 , z ) = E_n„ ,(p, 6 , z ) =

i ( m -1), n , m \", , /        0, n ,1 \", , /

( - i ) n ⁺ 1

' x

V 2n

которое можно реализовать с помощью дифракции гауссового пучка на СФП. Поэтому световые пучки, описываемые комплексной амплитудой (12), могут быть названы GOV [8,9].

3.3. Полые гауссовы оптические вихри

Можно получить явный аналитический вид через модифицированные функции Бесселя для комплексной амплитуды световых пучков, близких по форме к пучкам (12). Такие пучки можно сформировать с помощью дифракции полого гауссова пучка на СФП:

I k o3 I n x|----Г I exp in 6 +

V z to q J

ik p ²         p ²

2 R 1 ( z )    2 o ² ( z )

x (19)

x

1 1^ n ^- У ¹ 1 n ( У ) ⁺ yI n - 2 ( У ) , ^{V 2 J} 2           2

где y такое же, как в (12). Световые поля (19) с учетом вида порождающего их поля (14) можно назвать HGOV.

1 I Г I    I Г ²        I

E 0, n ,1 ( ^r , Ф , ^z = ⁰ ) = ;H “ I ^exp | ^-+ in ф I . ⁽¹⁴⁾ 2 п V toJ    I 2 o        J

3.4. Модифицированные элегантные пучки Лагерра-Гаусса

Эти пучки порождаются с помощью начального поля вида:

^E Y , n ,2 p + n ( r , Ф , z = ⁰ ) =

Чтобы получить комплексную амплитуду при z >  0 , получим сначала промежуточное соотношение. Для этого сравним два справочных интеграла, один из которых пропорционален функции Куммера [13]:

2 n

X 2 p + n r I

to

exp

¹ r r , . „ --7 + in ф

V 2 o²

^

J r ² exp ( - pr ² ) J n ( cr ) d r = cⁿp ⁽ n ^{+ 3 )} 2 2 ^{( n + 1 )}x

( n + 3 I_-1,        _[ n + 3          c | xr ----- Г (n +1), F -----, n +1,,

V 2 ...           ⁷¹¹ V 2            4 p J

Получим новый вид световых пучков как частный случай HyG пучков (2) при условии Y = - i ( 2 p - m + n ) , p - целое число ( p > - n /2 ) . Для этого воспользуемся известной связью между функцией Куммера и присоединенными многочленами Лагерра [10]:

1 F 1 ( - p , n + 1, x ) = ^^ny Lⁿ p ( x ) , ( n + p ) !

а второй интеграл получается путем дифференцирования обеих частей равенства [13]

где Lⁿ_p ( x ) - присоединенный многочлен Лагерра.

С учетом (21) из (10) следует:

^E 0, n ,2 p + n ( P ’ ⁶ , z )

(- i) n+1 P!

2n

^z o I -02 I^x zq j

x ---

I to q

n+2 p n2

I      t ² exp I in 6 + Д-- 1 I L n ( t ) ,

Световые пучки (27) описываются комплексной амплитудой, пропорциональной неполной гамма-функции, и поэтому мы назвали их Y HyG пучками. Световые пучки (27) порождаются начальным световым полем вида:

E 0, n , n — 2 ( r , Ф , ^z = ⁰ ) =

где t = 2y = ^kорД V2qzД .

Световые пучки, описываемые комплексной амплитудой (22), можно назвать meLG пучками. Об этих пучках упоминается в [2], но явного вида их не приведено. Мы называем эти новые световые пучки элегантными, так как аргумент многочлена Лагерра комплексный, как и у обычных eLG [6]. Но зависимость аргумента многочлена Лагерра в (22) от переменной z отличается от аналогичной зависимости в

2 п

ч n — 2 r I to J

^f r r . ■ „ exp-- 2 + in Ф

| 2о2

Заметим, что meLG пучки (22) переходят в Y HyG пучки (27) при p = — 1.

обычных eLG пучках [6]. Приведем для сравнения явный вид eLG пучков в принятых здесь обозначениях:

p ⁺ 1

E _eLG ( р , 6 , Z ) = ( - i ) p ⁺ 1 I^" I X

I zq J n 2n —        2

x I — т—_г — I 5 ² exp ( in 6 — 5 ) L n ( 5 ) ,

I to q z J

4. Моделирование

Формирование HyG-мод [1] с помощью дифракционных оптических элементов – непростая задача. Во-первых, аналогично модам Бесселя [11], HyG-моды имеют бесконечную энергию, а во-вторых, HyG-моды порождаются начальным световым полем (1), которое имеет особенность в начале координат ( о ^ ^ , m = — 1 ) :

1 I to I

^E y , n , — 1 ( ^r , Ф , ^z = ⁰ ) =           exp

’ ’                    2п|r J

I r I i y In    + in ф

I to J

. (29)

где 5 = — ik р ²Д2 q ² z ). Из сравнения (22) и (23) видно, что аргументы s и t отличаются своей зависимостью от координаты z . Это отличие возникает из-за того, что meLG пучки (22) порождаются начальным полем (20), а eLG пучки (23) порождаются начальным полем вида:

^E eLG ( r , Ф , z = ⁰ ) =

Поэтому на практике, чтобы сформировать HyG-моду, световое поле (29) следует ограничить кольцевой диафрагмой с радиусами R ₁ и R ₂ ( R ₁ < R ₂ ). Однако такое ограничение апертуры начального поля при некоторых параметрах не приводит к заметным искажениям HyG-моды. На рис. 1 показан вид радиального распределения интенсивности поля (29), ограниченного кольцевой диафрагмой, и интенсивности на расстоянии z =100 мм.

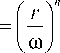
I r ²    К

exP I — 2о2 + inФ I Lp

f r ² I 1 2 о²J .

3.5. Гамма-гипергеометрические пучки

Приведем здесь еще один явный вид комплексной амплитуды, описывающей частный случай HyG пучков (2). Для этого воспользуемся связью между функцией Куммера и неполной гамма-функцией [10]:

1 F 1 ( n , n + 1, — x ) = nx ⁿ y ( n , x ) , где y ( v , x ) - неполная гамма-функция,

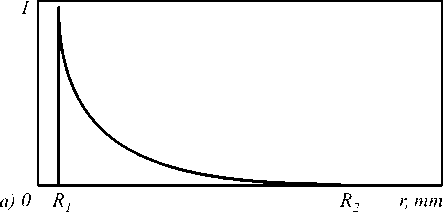
x

y ( v , x ) = J 1 " ¹ exp ( —^ ) d ^ .

С учетом (25) из (2) получим частный вид HyG пучков при y = i ( m + 2 ) :

E р, 6, z) = E,. Л p, 6, z) = i (m+2—n), n, m , ,            0, n, n—2 , ,

= ( — i ) n ^{+ 1} ( k to ² If k ptoI n _x

= 2 n I 2 z R 2 z ^J

б)

p, mm

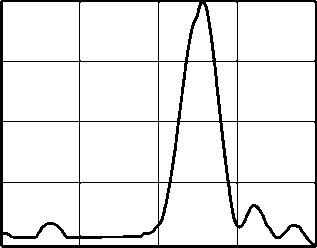
Рис. 1 Радиальное распределение интенсивности HyG моды (n=4, Y = - 10, m= - 1) при z=0 (а) и z=100 мм (б): точная HyG мода (1) и рассчитанная после ограничения апертурой (2)

f ikp2   . „I x exp —— + in6 Y

I 2 z       V

I k ор I n ,

| V2 qz J

.

При следующих параметрах расчета: 1 =532 нм, R ₁ =0,05 мм, R ₂ =1 мм, w =1 мм, число отсчетов

N =512; параметры HyG-моды: n =4, γ = - 10, среднеквадратичное отклонение точной интенсивности, полученной на основе уравнения (2), от рассчитанной с учетом ограниченной апертуры (рис. 1 б ) составляет 5,5%.

Реализация амплитудного распределения, показанного на рис. 1 а , для формирования HyG моды является неэффективным способом. Более энергетически эффективным и технологичным является формирование HyG моды с помощью фазового бинарного ДОЭ [14].

Функция пропускания такого ДОЭ может иметь следующий вид:

τ_{γ , n} ( r , φ ) =

I I r I                                              ,1

= sgn cos γ ln + n φ+ cr cos φ ,

I          'I w J                              I

где c – несущая пространственная частота.

На рис. 2 показана бинарная фаза ДОЭ (30) (диаметр 5 мм, n =7, γ =10, с =10 мм ^{- 1} , w =1 мм) ( а ) и рассчитанная картина дифракции на расстоянии z =700 мм от ДОЭ ( б ).

а)

б)

Рис. 2. Бинарная фаза ДОЭ (с=10 мм ^{- 1}) (а) и рассчитанная картина дифракции на расстоянии z=700 мм (б)

Из рис. 2 б видно, что при освещении ДОЭ (рис. 1 а ) плоской волной на некотором расстоянии формируются в основном две кольцевых картины дифракции, близкие к HyG модам с номерами n =7, γ =10 (большие кольца) и n = - 7, γ = - 10 (малые кольца). В каждый из двух пучков идет около 40% световой энергии.

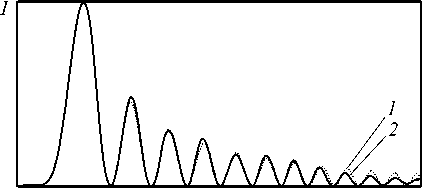
На рис. 3 показаны радиальные распределения интенсивности, рассчитанные для идеальной моды HyG (кривые 1) и сформированные с помощью бинарного ДОЭ (рис. 2 а ) (кривые 2) на расстоянии z =2000 мм: n =7, γ =10 (а) и n = - 7, γ = - 10 ( б ).

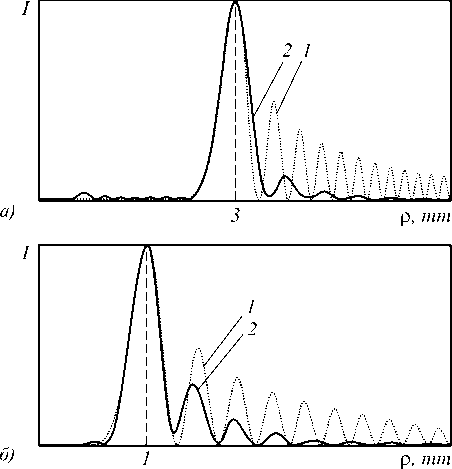
Рис. 3. Радиальные распределения интенсивности точных HyG-мод (кривые 1) и рассчитанных после бинарного

ДОЭ (рис. 2а) (кривые 2) на расстоянии z=2000 мм: n=7, γ =10 (а) и n= - 7, γ = - 10 (б)

Среднеквадратичное отклонение точных HyG-мод от рассчитанных на расстоянии z =2000 мм от бинарного ДОЭ (рис. 2 а ) составило 43% ( а ) и 35% ( б ). Таким образом, замена убывающей от r амплитуды функции (29) на постоянную в (30) приводит к заметной ошибке при формировании HyG пучка. Однако отличия касаются только боковых лепестков картин дифракции и почти не затрагивают основное кольцо.

• 5.    Эксперимент

  С помощью электронной литографии был изготовлен бинарный фазовый ДОЭ размером 5 × 5 мм с разрешением 10 мкм для длины волны 532 нм. На рис. 4. показано изображение центральной части микрорельефа этого ДОЭ, полученное с помощью интерферометра NewView 5000 Zygo co 100 -кратным увеличением.

0.000            mm            0.353

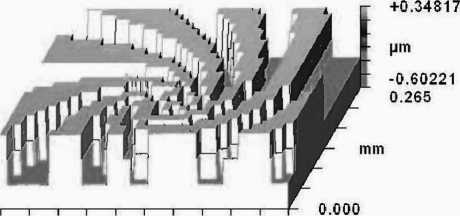
Рис. 4. Микрорельеф центральной части бинарного ДОЭ (рис. 2а) размером 353×265мкм в подложке из плавленого кварца

Требуемая высота микрорельефа в подложке из плавленого кварца (SiO 2 ) равна 578,3нм, а высота изготовленного рельефа колебалась от 572 до 583 нм. То есть бинарный ДОЭ изготовлен с высокой точностью — около 1%.

На рис. 5 показаны картины дифракции, сформированные после освещения ДОЭ плоским пучком света диаметром 4 мм от твердотельного лазера с длиной волны 532 нм и мощностью 500 мВт и измеренные на разных расстояниях от ДОЭ: 2000 мм (а), 2300 мм (б) и 3000 мм (в). Из рис. 5 видно, что картины дифракции по форме совпадают с расчетными картинами (рис. 2 в ) и что на достаточном удалении от ДОЭ оба световых пучка n =7, γ = 10 и n =-7, γ= - 10. ыслабмо еняются при распространении.

Из рис. 6 видно, что обе картины дифракции и их радиальные сечения удовлетворительно соответствуют друг другу, а среднеквадратичная ошибка составляет 27%.

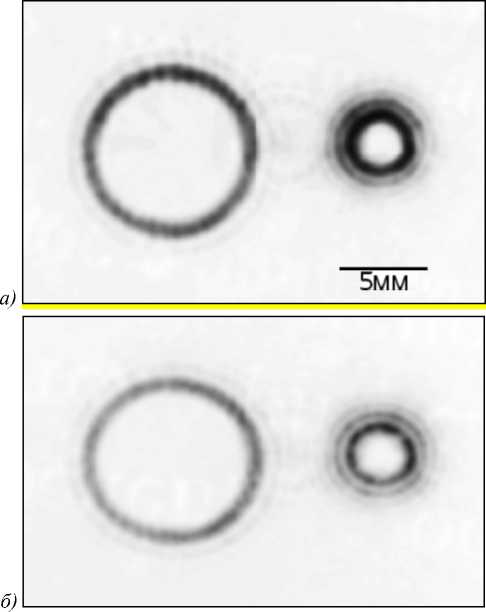
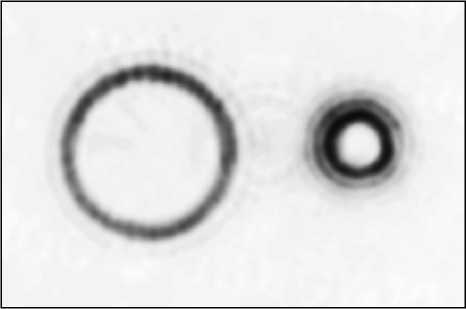
Рис. 5. Картины дифракции, сформированные ДОЭ (рис. 4) при освещении плоским пучком диаметром 4 мм ( λ = 532 нм) и зарегистрированные CCD-камерой на расстояниях 2000 (а), 2300 (б) и 3000 мм (в)

На рис. 6 показаны экспериментальная ( а ) и расчетная ( в ) картины дифракции плоской волны на ДОЭ для HyG-моды ( n =7, γ = 10 ) и их радиальные сечения интенсивности ( б и г соответственно).

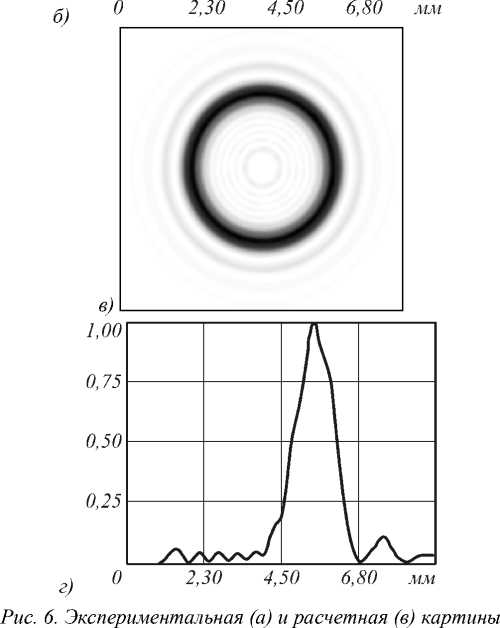
дифракции плоской волны на ДОЭ для HyG-моды (n=7, γ = 10 ) и их радиальные сечения интенсивности: экспериментальное (б) и расчетное (г)

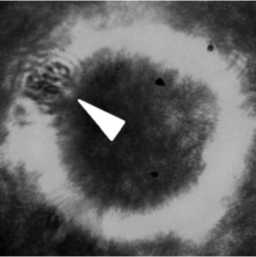
На рис. 7 показаны три фрагмента (разделенных временным интервалом в 15 сек) вращения полистиролового шарика диаметром 5 мкм, вращающегося по основному кольцу HyG пучка ( n =7, γ = 10 ), сформированного бинарным ДОЭ (рис. 4). Световое кольцо на рис. 7 после фокусировки микрообъективом × 40 имело диаметр 39 мкм.

б)

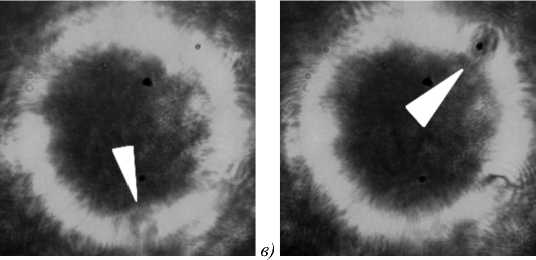
Рис. 7. Вращение полистироловой частицы диаметром 5 мкм (местоположение частицы показано белым треугольником) по основному кольцу картины дифракции для HyG пучка (n=7, γ =10), сформированной при дифракции плоской волны на

ДОЭ (рис. 4)

• 6.    Заключение

Получены явные аналитические выражения, описывающие параксиальные световые пучки, являющиеся частными случаями HyG лазерных пучков: mQBG, GOV, HGOV, meLG и γ HyG пучки. По технологии электронной микролитографии с точностью реализации высоты микрорельефа около 1% синтезирован бинарный дифракционный оптический элемент, приближенно формирующий HyG пучки. Бинарный ДОЭ рассчитывался как киноформ, то есть модуль кодируемой комплексной функции заменялся константой, а аргумент (фаза) комплексной функции сохранялся. В результате такой замены сформированные картины дифракции по форме совпадают с картинами дифракции для HyG пучков, хотя количественно заметно отличаются. Однако отличия касаются только боковых лепестков картин дифракции (периферийных колец) и почти не затрагивают основное кольцо. Теория и эксперимент находятся в удовлетворительном соответствии. Также экспериментально показана возможность вращения полистироловых шариков диаметром 5 мкм в световом кольце сформированного лазерного пучка.

Работа выполнена при частичной финансовой поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-Sa-06, грантов РФФИ №№ 07-07-97600, 08-07-99007 и Президента РФ № НШ-3086.2008.9.