Некоторые замечания, касающиеся эффективности дифференциации наночастиц в поле центробежных сил

В настоящее время наблюдается повышенный интерес к методам позиционирования дисперсных материалов на поверхностях, использования их для модифицирования различных материалов и для создания новых. Позиционирование частиц на поверхностях наиболее часто используется для биосенсоров [1; 2] и электроники [3; 4]. Более того, сортировка частиц, органелл и клеток разного размера является важным для многих биологических и медицинских применений.

Современные методы разделения частиц основаны на разности плотности и размера (размер-селективное осаждение [5], броуновская диффузия [6] и использование вибрационной сегрегации [7; 8]), на разности поверхностных свойств (высокоэффективная жидкостная хроматография [9]), на разности заряда в зависимости от размера (гель-электрофорез [10]), на разности диэлектрической постоянной в связи с размером частиц (диэлектрофорез [11, 12]), а также на акустическом импедансе (ультразвуковое разделение [13]). Однако наиболее распространено центрифугирование [14], особенно в области медицины и биологии. Использование данного метода разделения по размерам для наночастиц еще недостаточно хорошо изучено, требуется оценка эффективности метода и разработка средств для ее повышения.

Основы разделения в поле центробежных сил. Для повышения эффективности разделения час- тиц с характерным размером в десятки нанометров необходимо ввести некоторый параметр, численно характеризующий степень разделения частиц. Обычно для этого пользуются коэффициентом разделения

,                                                               (1)

в котором n 1 и n z – концентрации частиц двух сортов (размеров) и r 0 – радиус ротора центрифуги.

Пользуясь распределением Больцмана, пригодным с некоторыми ограничениями для нашего слу- чая [15],

где n – концентрация частиц в той точке ротора, где потенциальная энергия частицы имеет значение U, n 0 – концентрация частиц в том месте, где потенциальная энергия частицы равна нулю, можно найти соответствующие концентрации и, следовательно, коэффициент разделения q .

Следует заметить, что нижеприведенные выражения справедливы только для частиц с размером не более десятков нанометров и для реальной среды метод имеет определенные погрешности, в виду того, что рассматриваемая система не является идеальной с точки зрения термодинамики.

Частицы во вращающемся роторе центрифуги эквивалентны частицам, находящимся во внешнем силовом поле |F| - mw*r , где m – масса частицы, r – расстояние частицы от оси вращения. Вычис- лим потенциальную энергию молекулы в таком поле:

m ω ²r = – dU/dt , U = ∫ m ω ²R d R, U = – m ω ²R/2.

Так как помимо силового поля -r на частицы воздействует сила трения относительно других час- тиц и стенок ротора, то введем силу трения:

dU

dt

,

m ϖ ² r

- F_тр

F = m ϖ ² r - ^r F тр ,   m ϖ ² r - F тр

Тогда согласно распределению Больцмана (2) получим:

n1 = n10 exp(m1ω2R2/2kT –∫FсопротdR), n2 = n20 exp(m2ω2R2/2kT –∫FсопротdR), где n10 и n20 – концентрации частиц обоих размеров при R = 0.

Далее можно написать выражение для коэффициента разделения q и угловой скорости ω :

4          -a " ^'     2^     ~ • ^апглт- /

^ "2*"^ -^^ ”8  {^ив_ dД

-sf2(jnii - m^ Ждй-7                                     (3)

где R 0 – радиус ротора центрифуги.

Для того чтобы можно было воспользоваться выражением (3), нам нужно оценить интеграл от силы сопротивления ∫ F сопрот d R эмпирическим путем, воспользовавшись данными экспериментального разделения в поле центробежных сил.

На рис. 1–2 приведены гистограммы распределений по размерам порошков Т-05 и Т-20 «Тарко-сил» [14]. Образцы брались после центрифугирования из областей ротора, ближайших к его периферии (r = r 0 ) и оси вращения (r → 0). Скорость вращения ротора составляла 6000 об/мин или 628,3 рад/с, радиус ротора – 20 см, температура – 293 К. Кроме угловой скорости ω нам нужно определить коэффициент разделения q из приведенных распределений

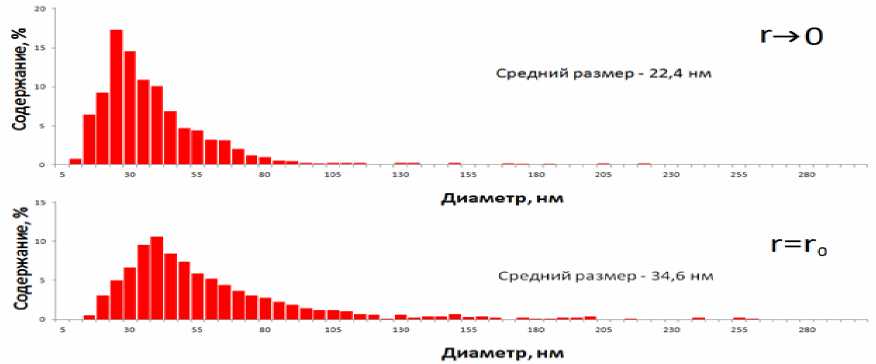
Рис. 1. Распределение по размерам порошка Т-05, взятого из области максимального радиуса ротора центрифуги (внизу, R=R0) и области, ближайшей к оси вращения (вверху, R=0)

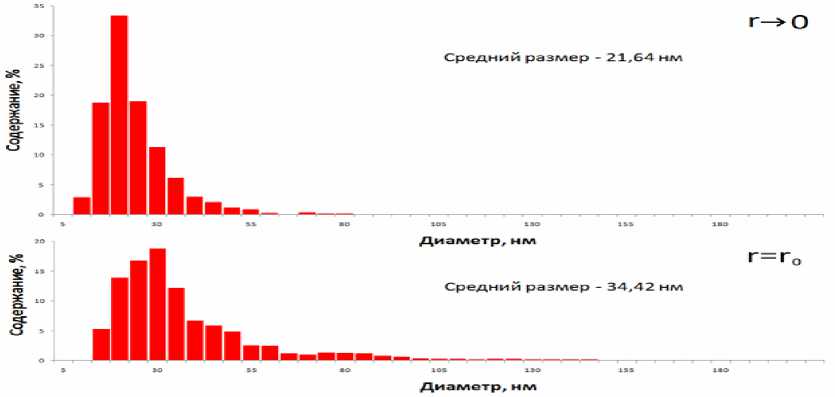
Рис. 2. Распределение по размерам порошка Т-20, взятого из области максимального радиуса ротора центрифуги (внизу, R=R0) и области, ближайшей к оси вращения (вверху, R=0)

Для определения коэффициента распределения примем частицы следующих размеров: 10∙10-9 м и 20∙10-9 м; 20∙10-9 м и 50∙10-9 м; 20∙10-9 м и 30∙10-9 м; 15∙10-9 м и 35∙10-9 м. Найдя относительное количество частиц всех размеров по рис. 1 и 2, по формуле (1) вычислим коэффициент разделения q для каждой пары размеров и его среднее значение (табл. 1).

Теперь, зная экспериментально определенные коэффициенты разделения q и угловую скорость ω , мы можем найти интеграл от силы сопротивления ∫ F _сопрот d R, выразив ее из уравнения (3):

F сопрот

( m ₁ - m ₂ ) ϖ ² r ² o

-

4 kT

¹₂ln q .

Таблица 1

Коэффициент разделения для различных размеров частиц

	Рисунок	Рис. 1				q (%)	Рис. 2				q (%)
	Концентрация n (%) при R=0 и R=R 0	R=0		R=R 0			R=0		R=R 0
		n 1	n 2	n 1	n 2		n 1	n 2	n 1	n 2
Сорт частиц	r 1 =10∙10-9 м	7	-	1	-	50	18	-	5,5	-	32
	r 2 =20∙10-9 м	-	17,5	-	5		-	18,5	-	17
	r 1 =20∙10-9 м	17,5	-	5	-	19,5	18,5	-	17	-	36
	r 2 =50∙10-9 м	-	4,5	-	6,5		-	1	-	2,5
	r 1 =10∙10-9 м	7	-	1	-	17	18	-	5,5	-	17
	r 2 =30∙10-9 м	-	12	-	9,5		-	7	-	12,5
	r 1 =15∙10-9 м	9	-	3	-	27,7	34	-	14	-	161
	r 2 =35∙10-9 м	-	10	-	12		-	3	-	7
Средний коэф. q						45 %

Рис. 3. Изображение наночастиц диоксида кремния, полученное на ПЭМ, подтверждает сферическое строение частиц

Массу частиц найдем из условия их сферичности (рис. 3), приняв плотность для аморфного диоксида кремния ρ = 2220 кг/м³ [3]:

3    ,

m* = Р*^

, m $ = p- /Trj1 .

В табл. 2 приведены значения сил трения для каждого вычисленного ранее значения коэффициента разделения q и соответствующих ему размеров частиц r 1 и r 2 .

Таблица 2 Расчет интеграла сил сопротивления частицам

q	r 1	r 2	∫ F сопрот d R
50 %	10∙10-9 м	20∙10-9 м	1,45∙10-16 Н∙м
19,5 %	20∙10-9 м	50∙10-9 м	2,43∙10-15 Н∙м
17 %	10∙10-9 м	30∙10-9 м	5,40∙10-16 Н∙м
27,7 %	15∙10-9 м	35∙10-9 м	8,20∙10-16 Н∙м
32 %	10∙10-9 м	20∙10-9 м	1,45∙10-16 Н∙м
36 %	20∙10-9 м	50∙10-9 м	2,43∙10-15 Н∙м
17 %	10∙10-9 м	30∙10-9 м	5,40∙10-16 Н∙м
161 %	15∙10-9 м	35∙10-9 м	8,20∙10-16 Н∙м
Среднее значение ∫ F соп р от d R			9,8∙10-16 Н∙м

Из табл. 2 видим, что интеграл от силы Стокса, силы трения между частицами, частицами и средой в роторе, а также между частицами и стенками ротора центрифуги сильно зависит от их размера, и в среднем составляет 9,8 ⋅ 10^-16 Н ⋅ м. Пользуясь полученным значением, теперь мы с легкостью можем приблизительно предсказывать угловую скорость ротора, необходимую для нужного нам коэффициента разделения частиц с соответствующим их размером, пользуясь выражением (3).

Так, при коэффициенте разделения, равном 80 % для частиц диоксида кремния с радиусом r 1 = 10 нм и r 2 = 20 нм, требуется угловая скорость ω = 1635 рад/с или n = 15630 об/мин (температура 293 К, радиус ротора 20 см).

На рис. 4 приведена зависимость центробежной силы от размера частиц на различных окружностях ротора при частоте вращения 6000 об/мин. На данной параболической зависимости наглядно видно, насколько сила зависит от размера частиц и радиуса ее нахождения.

Аналогичный вывод дает рассмотрение рис. 5. Только здесь приведена линейная зависимость центробежной силы от радиуса окружности ротора, вращающегося с частотой 6000 об/мин, при различных размерах частиц: 10, 50, 100 и 150 нм.

Эффективность пространственного перераспределения частиц охарактеризована рис. 6, на котором приведена зависимость пути частиц от времени центрифугирования для различного их размера при радиусе окружности 10 см и частоте вращения 6000 об/мин. Здесь мы видим параболические кривые для частиц различных диаметров. Абсолютный путь, пройденный частицами под действием силы Стокса и центробежной силы за 6000 с невелик, однако сильно различается для разных частиц.

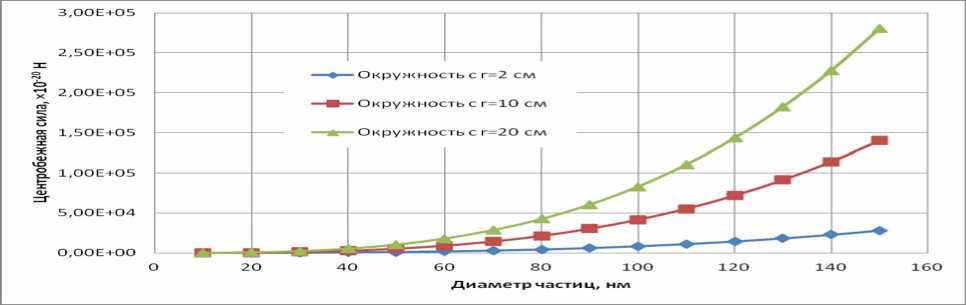
Рис. 4. Зависимость центробежной силы от размера частиц на различных окружностях ротора при частоте вращения 6000 об/мин

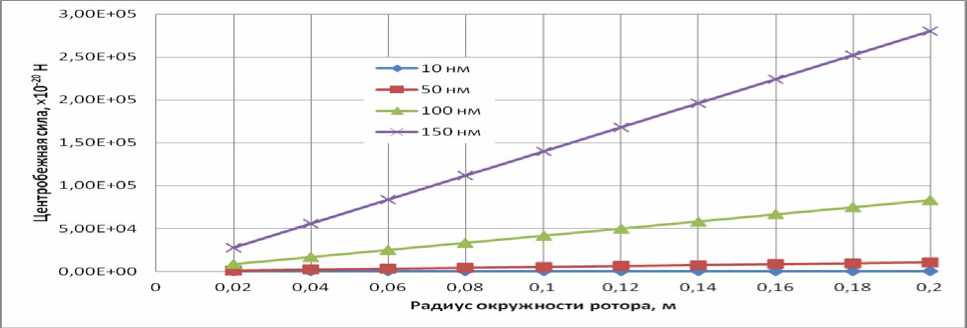
Рис. 5. Зависимость центробежной силы от радиуса окружности ротора, вращающегося с частотой 6000 об/мин, при различных размерах частиц

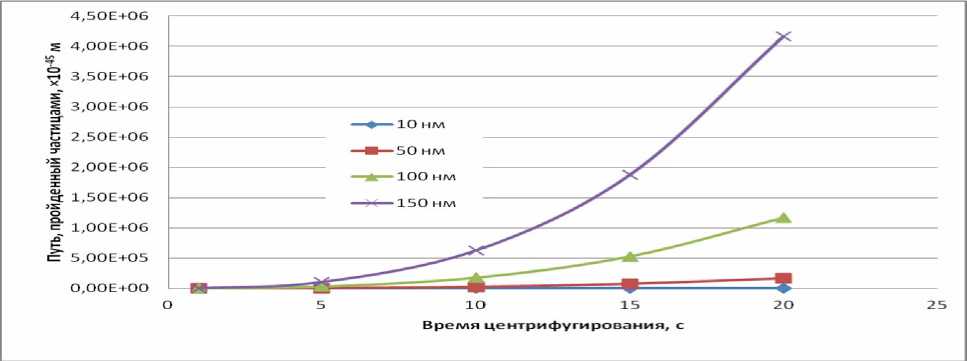
Рис. 6. Зависимость пути частиц от времени центрифугирования для различного их размера при радиусе окружности 10 см и частоте вращения 6000 об/мин

Расчет выполнен на основании следующего: частицы в начале пути двигаются равноускоренно до тех пор, пока центробежную силу не компенсирует сила Стокса, т. е.

m ω ²R = 6 π r ην .                                  (5)

Подсчитав центробежную силу, можно найти установившуюся скорость частиц с радиусом r. Так, для частицы диаметром 20 нм центробежная сила на радиусе R = 10 cv равна 2,07⋅10-16H, а ее примерная установившаяся скорость ν = 5,6⋅10-7M/c. Путь, пройденный частицей за время t исходя из уравнения (5) будет mw’Rt 5 = —--

6itrq .                                             (6)

Время и путь, проходимый частицей равноускоренно, невелик, поэтому им можно пренебречь. Из выражения (6) можно оценить время, необходимое для разделения частиц. При радиусе ротора 5 см та же частица в 20 нм, находящаяся около оси вращения, осядет на дно через t = 810 c. Расчет выполнен для воды.

Приведенные зависимости несколько неточны, т. к. центробежная сила при движении частицы к большему радиусу непостоянна. Однако при небольших перемещениях, используемых в центрифугах, данным изменением можно пренебречь. Приведенный способ достаточно прост и наиболее подходит именно для оценки разделений твердых частиц. Хотя в статье сила трения вычислена для частиц диоксида кремния, метод применим для любых материалов. Так, более точный метод с решением уравнения Ламма наиболее применим для оценки размеров частиц в коллоидных системах при ультрацентрифугировании [16].

Выводы

Рассмотренное исследование позволяет выявить зависимости частоты вращения ротора центрифуги, его диаметра и параметров частиц (их радиуса или массы) с коэффициентом разделения наночастиц, временем разделения, что актуально в плане практического применения в нанотехнологиях.