Нелинейная динамика механических систем: от асимптотических методов к детерминированному хаосу
Автор: Петров Л.Ф.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Механика
Статья в выпуске: 3 (35) т.9, 2017 года.
Бесплатный доступ
Как продолжение и развитие исследований в области асимптотических методов нелинейной механики рассматриваются задачи существенно нелинейной динамики ме- ханических систем с одной и несколькими степенями свободы. Рассматриваются авто- номные и неавтономные системы, учитываются разнообразные виды колебаний, их со- четания и нелинейное взаимодействие. Обсуждается алгоритм поиска и анализа устой- чивости периодических решений существенно нелинейных систем. Приводятся поста- новки некоторых задач динамики механических систем в существенно нелинейном ва- рианте, в частности колебания с прощелкиванием потерявшего устойчивость прямоли- нейного стержня с учетом нескольких форм колебаний, а также результаты численных экспериментов по исследованию динамики существенно нелинейных механических си- стем, в том числе колебания с перескоком. Обсуждаются способы управления детерми- нированным хаосом, качественные аналогии и возможные обобщения эффектов, обна- руженных в нелинейных динамических моделях механики, на задачи экономической и социальной динамики.
Нелинейная динамика, колебания с прощелкиванием, периодические решения, детерминированный хаос
Короткий адрес: https://sciup.org/142214981
IDR: 142214981 | УДК: 534.1
Текст научной статьи Нелинейная динамика механических систем: от асимптотических методов к детерминированному хаосу
Результаты, полученные с помощью асимптотических методов нелинейной механики [1], позволили обнаружить много новых по сравнению с линейными моделями эффектов. Среди этих результатов можно выделить возможность существования нескольких устойчивых и неустойчивых динамических режимов при одинаковых параметрах динамической системы и внешнего возмущения, неизохронность собственных колебаний, то есть зависимость частоты собственных колебаний от их амплитуды, существование субгармонических и уль-трагармонических решений, бифуркации решений, существование устойчивых автоколебаний с ограниченной амплитудой, эффекты синхронизации и захватывания в динамических системах. Часто при решении динамических задач механики от уравнений в частных производных производится переход к обыкновенным нелинейным дифференциальным уравнениям [2]. Некоторые задачи приводятся к уравнению Дюффинга, с помощью которого исследованы многие нелинейные эффекты [3], [4]. Анализ решений этого уравнения позволяет проследить эволюцию задач нелинейной механики от квазилинейных постановок к изучению существенно нелинейных эффектов. Особый интерес представляют механические системы с отрицательной жесткостью, для которых при колебаниях реализуется режим перескока или прощелкивания. В механике это состояние реализуется после потери статической устойчивости, при этом меняется структура фазового пространства, появляется возможность разнообразных колебаний около нескольких положений равновесия. В технике такие задачи могут реализовываться иначе, но остается возможность колебаний около различных положений равновесия [5]. К таким задачам квазилинейный подход неприменим, они по сути своей являются существенно нелинейными.
2. Существенно нелинейные колебания механических систем с одной степенью свободы
Рассмотрим последовательное усложнение постановок задач механики от линейных к квазилинейным и существенно нелинейным. Будем считать, что задача механики деформируемого твердого тела с помощью процедуры Бубнова–Галеркина преобразована от уравнений в частных производных к обыкновенным дифференциальным уравнениям. Если учитывается одна форма колебаний, то получается система обыкновенных дифференциальных уравнений второго порядка, соответствующая одной степени свободы исходной механической системы. При учете N форм колебаний получаем систему обыкновенных дифференциальных уравнений порядка 2 N . Рассматриваемые модели могут быть линейными, квазилинейными, существенно нелинейными. Так, например, колебания с одной степенью свободы прямолинейного стержня под воздействием изменяющихся во времени продольных и поперечных сил описываются уравнением
x(t ) + ш 2 (1 + P о + P sin( w p t + а )) х ( t ) + b i ( x ( t )) + үх 3 ( t ) = W sin( wt ) . (1)
Здесь x ( t ) — искомая амплитуда колебаний по первой форме, зависящая от времени t , ш о — собственная частота, P о — постоянная растягивающая (сжимающая при P о < 0 ) сила, направленная вдоль оси стержня, P sin( w p t ) — продольная периодически меняющаяся во времени сила, которая может стать причиной возникновения параметрических колебаний, b i ( х ( t )) — в общем случае нелинейные диссипативные силы, зависящие от скорости, үх 3 ( t ) — нелинейная составляющая модели, W sin( wt ) — внешняя периодическая по времени поперечная сила, α — сдвиг фазы. Из этой существенно нелинейной модели в случае ү = 0, b i ( х ( t )) = bx(t ) получаем линейную модель, при 0 < ү ^ 1 — квазилинейную.
Вариант bi(х(t)) < 0 соответствует физическому эффекту не диссипации, а «подкачки» энергии в динамическую систему, при этом могут возникнуть автоколебания. В случае Pо < — 1 получаем вариант существенно нелинейной модели — систему с отрицательной жесткостью, которая соответствует поперечным колебаниям потерявшего статическую устойчивость стержня, колебания при этом могут происходить с прощелкиванием (перескоком).
Для системы (1) могут выбираться два варианта: задача Коши, когда задаются начальные условия, или задача об отыскании периодического решения. Эта система является математической моделью с одной степенью свободы для переходных процессов (задача Коши), вынужденных колебаний (отыскание периодических решений при W = 0 ), параметрических колебаний (при P = 0), автоколебаний (при b 1 ( x ( t )) < 0), колебаний с перескоком (при P о < — 1 ). При этом в нелинейном варианте, когда не выполняется принцип суперпозиции, реализуется нелинейное взаимодействие (но не сложение) перечисленных видов колебаний. Так, например, при численных экспериментах в нелинейной системе проявляется эффект снижения результирующей амплитуды за счет взаимного гашения различных видов колебаний. Для линейной системы аналогичный эффект, называемый динамическим гашением колебаний, реализован в системе большей размерности с двумя степенями свободы [6] .
Численное решение задачи Коши для системы (1) реализовано во многих пакетах программ в виде алгоритмов типа Рунге–Кутты различных порядков с автоматическим выбором шага при задаваемой пользователем допустимой погрешности. Исключая из рассмотрения жесткие системы, системы с малым параметром при старшей производной, будем считать, что численное решение задачи Коши может быть построено с помощью упомянутых стандартных программ.
3. Построение и анализ устойчивости периодических решений систем существенно нелинейных обыкновенных дифференциальных уравнений
Построение периодических решений для нелинейных систем вида (1), то есть анализ установившихся колебаний (вынужденных, параметрических, автоколебаний, их нелинейных взаимодействий), является более сложной задачей, чем исследование переходных процессов (задача Коши). В подобных системах могут реализовываться субгармонические, ультрагармонические, субультрагармонические колебания с разнообразными периодами [4]. Для автоколебаний период решения подлежит определению, для вынужденных и параметрических колебаний период решения связан с периодом внешнего или параметрического воздействия. При нелинейном взаимодействии автоколебаний и вынужденных, параметрических колебаний решение может иметь сложный характер, определяемый несколькими видами колебаний и нелинейными характеристиками системы. Могут также проявляться эффекты захватывания частоты [7].
Для численного построения периодических решений существенно нелинейных автономных и неавтономных систем обыкновенных дифференциальных уравнений использован алгоритм, основанный на отыскании начальных условий, соответствующих периодическому решению [8]. Такой подход позволяет ограничиться построением искомого периодического решения только на одном периоде, что снижает вычислительные трудности построения решения с заранее ограниченной погрешностью. Неподвижная точка отображения, соответствующего системе обыкновенных нелинейных дифференциальных уравнений, определяется либо методом Ньютона, либо с помощью оптимизационных процедур минимизации невязки.
Отметим свойства искомых решений, которые соответствуют физическому смыслу поведения динамической системы, но и усложняют формализацию алгоритма их поиска:
- возможно существование нескольких устойчивых и неустойчивых периодических решений при одних и тех же параметрах системы;
- разнообразный вид решений — гармонические различных периодов, субгармонические, ультрагармонические, субультрагармонические, детерминированный хаос;
- бифуркации решений при реализации метода продолжения по параметру;
- проявления эффекта перемежаемости для хаотического поведения решений.
4. Взаимодействие автоколебаний и вынужденных колебаний
Кроме того, отметим отсутствие гарантий сходимости итерационных процедур отыскания неподвижной точки, а для неустойчивых решений — уход численного решения с неустойчивой траектории. Учитывая эти особенности, алгоритм отыскания периодических решений систем существенно нелинейных обыкновенных дифференциальных уравнений реализован в виде интерактивной процедуры [9]. Пользователь получает информацию о ходе вычислительного процесса и на основании этой информации имеет возможность вмешиваться в работу алгоритма и менять параметры системы и вычислительных процедур. Анализ устойчивости найденных периодических решений проводится с помощью определения характеристических показателей Ляпунова (или мультипликаторов) для соответствующей системы в вариациях. Отметим, что алгоритм анализа устойчивости конечный, алгоритм поиска периодического решения итерационный, без гарантий сходимости и учитывающий возможность существования нескольких устойчивых и неустойчивых периодических решений различных периодов при одних и тех же параметрах системы и внешних воздействий.
Конкретный вид и величина нелинейных зависимостей в анализируемой системе уравнений не оговаривается, требуется лишь, чтобы используемые программные средства решения задачи Коши на одном периоде искомого решения позволяли строить это решение с определяемой пользователем точностью.
В рамках рассматриваемого подхода могут анализироваться решения линейных, квазилинейных, существенно нелинейных систем. Это позволяет проводить сравнение решений, получаемых асимптотическими методами и численно, с относительной погрешностью не хуже 10 ~ 5 . Естественно, при малых нелинейных слагаемых решения, получаемые асимптотическими и численными методами, будут близки. По мере роста нелинейности наблюдается увеличение различий в решениях, что позволяет определить сферу применимости количественных результатов, получаемых асимптотическими методами Количественные результаты такого сравнения для уравнения Дюффинга с различными уровнями нелинейности приведены в [8]. Линейные системы, имеющие аналитическое решение, используются как тестовые задачи.
в нелинейной системе с одной степенью свободы
В качестве примера приведем результаты решения задачи о взаимодействии автоколебаний и вынужденных колебаний. Для уравнения
x(t ) + x ( t ) — 0 , 2 x ( t ) + ( x ( t )) 3 + 30 x 3 ( t ) = W sin(3 t ) , (2)
которое учитывает взаимодействие автоколебаний и вынужденных колебаний, при небольших значениях амплитуды внешнего воздействия W решение соответствует автоколебаниям, при W ^ 1 колебания соответствуют вынужденным. При W = 1 обнаружены два принципиально различных устойчивых решения. Первое из них соответствует вынужденным колебаниям, имеет период внешнего воздействия T = 2 п/ 3 и фазовую траекторию типа эллипса. Второе устойчивое решение (рис. 1) имеет период 2 T. Это решение оказывается устойчивым и при W = 0 . 9. Первое решение при этом неустойчиво.
Отметим, что при тех значениях параметров системы, при которых реализуется странный аттрактор [10], отсутствуют устойчивые периодические решения, но там определяются разнообразные неустойчивые периодические режимы. Алгоритм построения периодических решений быстрее сходится к одному из устойчивых решений (если они есть), чем к любому из неустойчивых. Это является следствием ухода вычислительной процедуры решения задачи Коши с неустойчивой траекторией.
Результаты численных экспериментов по управлению видом решений в зоне странного аттрактора с помощью изменения параметров системы и/или внешнего воздействия четко отражают физический смысл динамического процесса. Так, например, увеличение параметра диссипации системы приводит к уменьшению зоны странного аттрактора — диссипация подавляет хаотическое поведение решений, сложные полигармонические решения при увеличении диссипации заменяются более простыми гармоническими решениями.
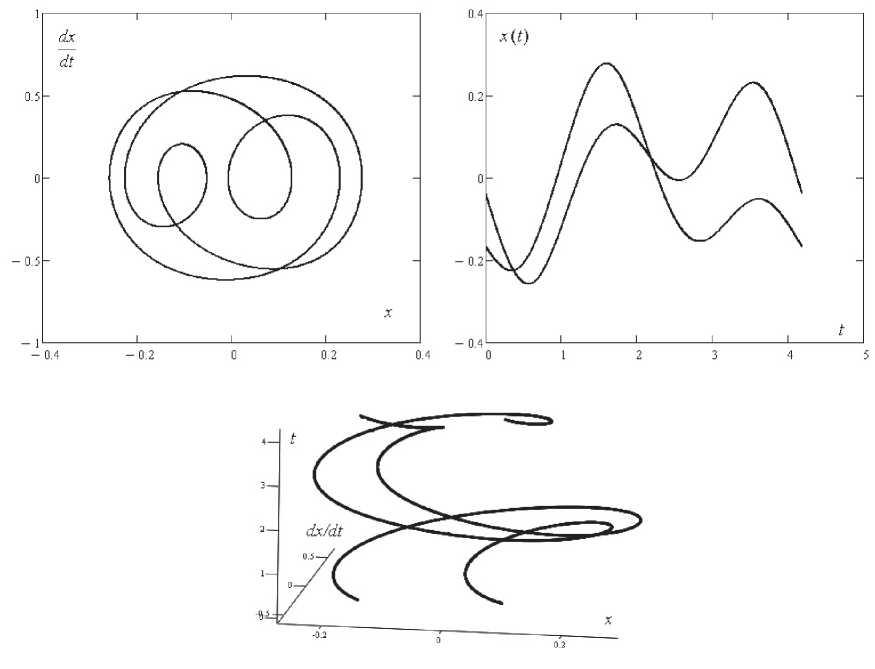
Рис. 1. 2 T -периодические устойчивые решения системы (2) при W = 0 . 9; W = 1 . 0
Аналогичный эффект наблюдается при увеличении амплитуды внешнего воздействия, сильное внешнее воздействие «навязывает» системе вид решения. При этом такое решение, определяемое сильным внешним воздействием, является устойчивым, и, следовательно, детерминированный хаос не может существовать.
Возвращаясь к постановке задач нелинейной динамики механических систем, отметим, что использование одной формы колебаний и, соответственно, исследование системы с одной степенью свободы оставляет ряд вопросов о влиянии на динамическое поведение отброшенных форм колебаний. Эта проблема актуальна даже для относительно простой одномерной по координатам задачи механики — поперечных колебаний прямолинейного стержня [11]. Для более сложных объектов — пластин и оболочек — необходимо учитывать влияние форм колебаний по двум координатам [2].
5. Колебания существенно нелинейных механических систем с несколькими степенями свободы
Рассмотрим (рис. 2), учитывая несколько форм колебаний, задачу о вынужденных поперечных колебаниях прямолинейного стержня длины L с постоянным поперечным сечением S, моментом инерции поперечного сечения I, материал стержня упругий и имеет модуль Юнга Е, плотность р. Ось у совместим с осью стержня. Пусть край стержня у = 0 свободно оперт, а край у = L сдвинут вдоль оси у на величину D, причем D ^ L, и закреплен в этом положении с выполнением условия свободного опирания. Стержень в продольном направлении может быть недеформирован (D = 0), сжат (D < 0) или растянут (D > 0). Предположим, что геометрия поперечного сечения стержня такова, что все его движения происходят в одной плоскости. Если стержень при смещении края y = L в сторону сжатия (D < 0) потерял статическую устойчивость, его ось будет представлять собой плоскую кривую w(у), в ином варианте ось стержня в отсутствие нагрузки прямолинейна. На стержень в этой плоскости действует поперечная T -периодическая по времени t нагрузка q(y,t) = q(y,t + T)•
Функцию w ( y,t ), определяющую геометрию оси стержня при колебаниях, представим в виде, учитывающем участие в колебаниях N форм:
N
w ( y,t ) = V S [ x 1 ( t ) sin( ny/L ) + y^ X m ( t ) sin( mny/L )] , (3)
m =2
где X j ( t ) — искомые функции времени.
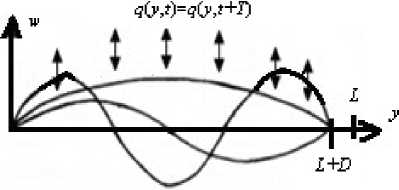
Рис. 2. Геометрия оси стержня с учетом нескольких форм колебаний
Рассматривая геометрию изогнутого стержня и применяя принцип возможных перемещений, получим [11]:
L ∂ 2 w ∂ 2 δw L 1 L ∂w 2 D ∂w ∂δw L ∂ 2 w
"^ 0o EI dy 2 dy 2 dy 0o ES ( 2 L 0o ( dy ) dy + L + D ) dy dy dy 0o P S dt 2 6wdy +
+ Юо P q ( y,t ) "wdy = 0;
Pq(y,t) = -nw( y,t) + q(y,t), где η — коэффициент диссипации.
Учитывая соотношения (3) в уравнении принципа возможных перемещений, можно получить систему нелинейных обыкновенных дифференциальных уравнений относительно функций X j ( t ):
X j ( t )+ j 2 ( k 2 j 2 + D 1 ) X j ( t )+ X j ( t ) j— ^ m 2 X 2 m ( t )+ 6 I X j ( t ) = 2 Q j ( t ) / 2 , j = 1 ,...,N. (4) 4 m =1 pL ^ S
Здесь ц 2 = En 4 S/ ( pL 4 ); k 2 = I/S 2 ; D 1 = DL/Sn 2- 6 1 = 6L/ ( ^pS );
Q j ( t ) = fo q ( y,t )sin( jn y /L ) dy .
Для системы обыкновенных нелинейных дифференциальных уравнений (4) размерности 2 N ставится задача отыскания различных mT -периодических решений ( m = 1 , 2 ,... ,m < то ) и проверки их устойчивости. В случае аппроксимации прогиба одним первым слагаемым ряда (3) получаем уравнение Дюффинга с одной степенью свободы. В существенно нелинейной постановке при D < 0 это уравнение исследовано Ф. Холмсом [10], при D > 0 — Б. И. Крюковым [4]. В обоих вариантах обнаружены как разнообразные устойчивые и неустойчивые периодические решения, так и хаотическое поведение.
Переходя к численному исследованию поперечных существенно нелинейных колебаний стержня с учетом нескольких степеней свободы, отметим, что при D < 0 (стержень сжат) в отдельных или всех уравнениях системы (4) возможно появление отрицательного коэффициента при линейном слагаемом X j ( t ), что соответствует модели системы с отрицательной жесткостью и появлению в фазовом пространстве дополнительных особых точек.
Внешнее воздействие принималось в виде q ( y, t ) = W sin wt sin ny/L , при этом Q i ( t ) = 0, Q j ( t ) = 0 ( j = 2 , 3 ,...,N ). При численной реализации учитывались два и три слагаемых в аппроксимации прогиба (3) ( N = 2 , N = 3). Среди полученных результатов отличными от тождественного нуля оказывались одна или две формы колебаний. Так, например, при наборе параметров, соответствующем колебаниям с перескоком потерявшего статическую устойчивость в результате действия продольной сжимающей силы стержня ( D 1 = — 0 , 011; к 2 = 0 , 001; L = 1; 5 1 = 0 , 3; Q i = 1) при частоте w < 0 , 45 и w > 0 , 8 колебания происходили только по первой форме, вторая форма x 2 ( t ) = 0. Однако при 0 , 45 < w < 0 , 8 в колебания вовлекается и вторая форма x 2 ( t ) = 0 (рис. 3).
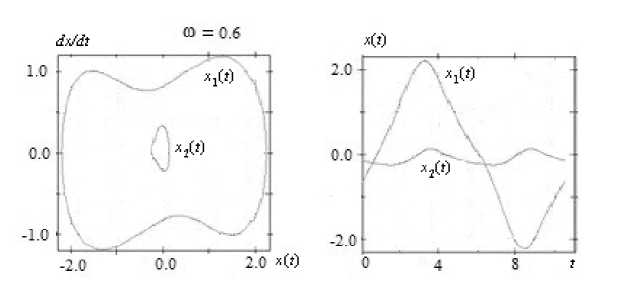
Рис. 3. Фазовые траектории и один период решения системы (4) при колебаниях с прощелкиванием с учетом нескольких форм
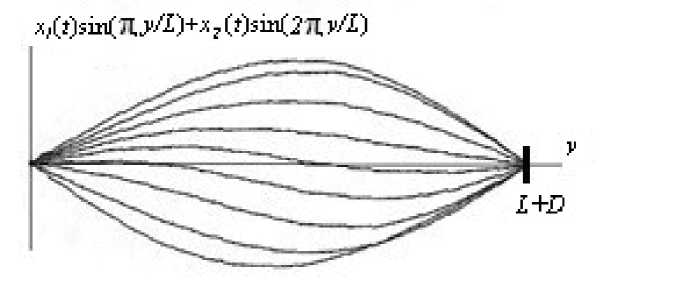
Рис. 4. Геометрия оси стержня в разные моменты при колебаниях с прощелкиванием с учетом нескольких форм
При этом сложение двух форм колебаний (рис. 4) показывает, что стержень проходит неустойчивое прямолинейное состояние по второй форме.
При других значениях параметров динамика стержня меняется от простых гармонических колебаний до хаотических движений. На рис. 5 приводится одно из устойчивых 2 T -периодических решений системы (4). Это решение получено при следующих значениях параметров системы: к 2 = 0 , 001 , D i = — 0 , 011 , 5 1 = 5 2 = 0 , 04 , Q = 1 , w = 0 , 6. Отметим, что для обеих подсистем при таких значениях параметров коэффициенты при x i ( t ) , x 2 ( t ) отрицательны (стержень сжат и потерял статическую устойчивость), особая точка (0 , 0) имеет седловой характер.
В другом случае, когда эти коэффициенты положительны (стержень растянут), особая точка (0, 0) имеет характер устойчивого фокуса. В этом случае в процесс колебаний вовлекаются обе подсистемы в случае сильной нелинейности. На рис. 6 приводится одно из устойчивых 3T-периодических решений системы (4), полученное при следующих значениях параметров системы: к2 = 0, 5, D1 = 0, 5, 51 = 52 = 0, 1, Q = 100, w = 1. Эти результа- ты качественно соответствуют и являются обобщением на многомерный случай сложных полигармонических решений одномерного уравнения Дюффинга [4].
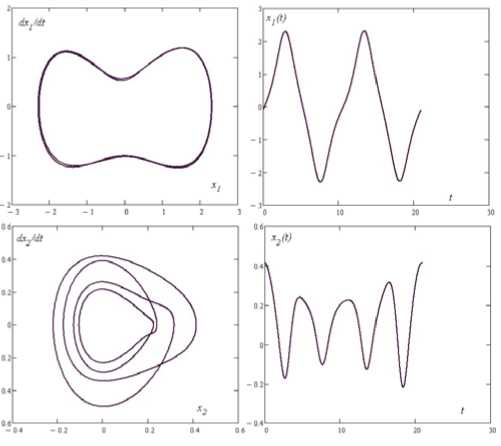
Рис. 5. Одно из устойчивых 2 T -периодических решений системы (4) при к 2 = 0 , 001 , D 1 = — 0 , 011 , 5 1 = 5 2 = 0 , 04 , Q = 1 , ш = 0 , 6
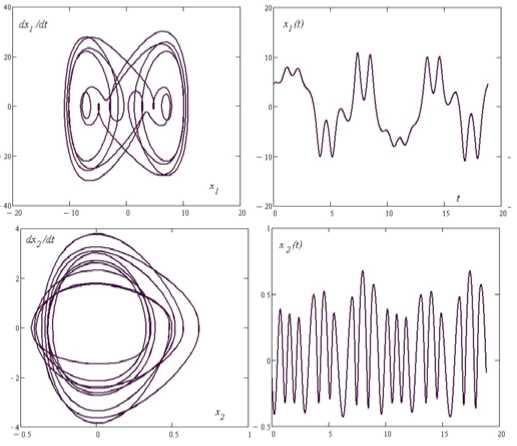
Рис. 6. Устойчивое 3 T -периодическое решение системы (4) при к 2 = 0 , 5 , D 1 = 0 , 5 , 5 1 = 5 2 = 0 , 1 , Q = 100 , ш = 1
6. Возможные обобщения
Отметим, что методология анализа динамических систем применима к гораздо более широкому классу задач, чем задачи нелинейной механики [5], [7], [8], [12], [13]. Для разнообразных приложений исторически прослеживается тот же сценарий уточнения моделей, что и в механике — линейные, квазилинейные, существенно нелинейные модели, последовательное увеличение размерности системы. Для задач механики обнаружен и подтвержден качественно и количественно ряд эффектов, проявляющихся в нелинейных моделях — бифуркации решений, потеря статической и динамической устойчивости, странный аттрактор, нелинейное взаимодействие различных видов и форм колебаний, эффекты синхро- низации движений. Для других приложений можно констатировать только качественные аналогии — экономический кризис как потеря устойчивости, поведение экономических индикаторов как автоколебания в окрестности линии тренда, информационное влияние на финансовый рынок как аналог внешнего воздействия в механике, синхронизация в толпе (например, бурные аплодисменты, переходящие в овацию, поведение фанатов, быстрый рост количества просмотров одного из многих постов в социальных сетях) и так далее. Если хаос в механике является равноправной формой поведения механической системы наряду со статикой и регулярной динамикой, то хаос в более сложной динамической системе (например, экономике и социуме) является приоритетной формой существования такой системы. Полное устранение хаоса (жесткая плановая экономика, диктатура в социуме, цензура в средствах коммуникации) ведет к деградации и застою экономики, социума, культуры, подавлению полезных инициатив и новых направлений бизнеса. Недостаточное регулирование в экономике и социуме (аналог внешнего воздействия и диссипации в механике) ведет к неуправляемому хаосу в экономике, анархии в социуме. Приведенные качественные аналогии, наблюдаемые в реальных экономических и социальных системах, в отличие от моделей механики не имеют точных количественных оценок и пока остаются только наблюдаемыми аналогиями.
Список литературы Нелинейная динамика механических систем: от асимптотических методов к детерминированному хаосу
- Моисеев Н.Н. Асимптотические методы нелинейной механики. М.: Наука, 1981.
- Вольмир А.С. Нелинейная динамика пластинок и оболочек. М.: Наука, 1972.
- Kovacic I., Brennan M.J. The Duffing Equation: Nonlinear Oscillators and their Behaviour. John Wiley and Sons, 2011.
- Крюков Б.И. Вынужденные колебания существенно нелинейных систем. М.: Машиностроение, 1984.
- Мун Ф. Хаотические колебания. М.: Мир, 1990.
- Бабаков И.М. Теория колебаний. М.: Дрофа, 2004.
- Блехман И.И. Синхронизация в природе и технике М.: URSS, 2015.
- Петров Л.Ф. Методы динамического анализа экономики. М.: Инфра-М, 2010.
- Petrov L.F. Interactive computational search strategy of periodic solutions in essentially nonlinear dynamics//Springer International Publishing Switzerland. Interdisciplinary Topics in Applied Mathematics, Modeling and Computational Science, Springer Proceedings in Mathematics and Statistics. 2015. V. 117, P. 355-360.
- Holmes P.J. A nonlinear oscillator with a strange attractor//Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 1979. V. 292, N 1394. P. 419-448.
- Petrov L.F.Coupled multidimensional strongly nonlinear forced oscillations with dynamic jumping//Journal of Coupled Systems and Multiscale Dynamics. 2013. V. 1, N 3. P. 351-357.
- Моисеев Н.Н. Математика в социальных науках//Математические методы в социо-логическом исследовании. 1981. С. 10-24.
- Милованов В.П. Синергетика и самоорганизация: Социально-экономические системы. М.: URSS, 2015.


