Нелинейная фильтрация для специального и степенного законов сопротивления среды

Система, уравнений, описывающая двумерное установившееся фильтрационное движение несжимаемой жидкости в пласте, имеет вид [1]:

можем написать:

∂ψ ∂x

—v = —w sin 9,

∂ψ

—— = u = w cos 9, ∂y

∂H	Ф ( w )
	-u
∂x	w
∂H	Ф ( w )
	-v
dy	w
∂u	∂v
--+	— = 0 .
∂x	∂y

Здесь H — обобщенный напор, w = ( u,v ) — скорость фильтрации, w = |w| , Ф( w ) — закон сопротивления среды, для которого Ф ( w ) > 0, Ф 0 ( w ) > 0, причем в нуль левые части последних неравенств могут обращаться лишь при w = 0.

Из третьего уравнения (1) и формулы Грина.

дХ + dx ⁺ lyydy = /^{( —}v ) G                   ∂G ⁺

d + u dy,

где dG ⁺ — положительно ориентируемая граница области G. имеем

( —v ) dx + u dy = 0 .

∂G ⁺

Последнее означает, что выражение dф = = ( —v ) dx + udy является полным дифференциалом, криволинейный интеграл от которого по пути Г не зависит от формы этого пути, и поэтому существует потенциал

^ф =

J ^{( —v} ) ^{dx + udy}

Γ

и

дф дф

∂x v, ∂y

Из последних равенств для функции тока ф мы

где 9 — угол между w и положительным направлением оси Ox. Следуя [1,2], получаем систему

д9   Ф(w) dw   0  д9   wФ0(w) dw дф   w2 dH   ’ dH   Ф2 (w) дф

Перейдем к переменным 9 и w . Для этого положим ф = ф ( w, 9 ) 11 H = H ( w,9 ). продпффс'реп-цируем последние равенства по ф и H и запишем полученные равенства, в виде двух линейных сис

тем:

{дф дю , дф дф _ 1  ( дН дю , дН дб дю дф + дб дф = 1 ’   дю дф + дб дф = 0 ’

∂ψ ∂w  ∂ψ ∂θ       ∂H ∂w  ∂H ∂θ дю дН + дб дН = 0 ’ I дю дН + дб дН  1.

Их общий определитель w = 0 в силу (2) отрицателен, т. к.

А =	дю дб дф дф		∂w ∂θ -	dw д9
	∂w ∂θ дН дН		∂ψ ∂H	∂H ∂ψ
=	dw / w Ф 0 ( w ) дф \ Ф2 ( w )		dw 3 ∂ψ	dw /Ф( w ) dw 3 dH у w 2 dHj =
	w Ф 0 ( w Ф2( w		) / dw 3 w	2 - ф г ^ 32 <  0 w 2 ∂H
По правилу Крамера.
	∂ψ	1	∂θ 1 дф	1 д9
	dw	А	П дб 0 дН	А dH ’
	∂ψ	1	дю I дф 1	1 dw
	д9	А	дю п дН 0	А dH ’
	dH	1	о дф 0 дф	1 д9
	∂w	А	∂θ 1 дН	А дф ’
	∂H	1	∂w дф 0	1 dw
	д9	А	дю I дН 1	А дф ’

Работа выполнена при поддержке АВЦП «Развитие научного потенциала высшей школы», проекты .№ 2.1.1/11133 и 2.1.1/12968.

Из последних равенств мы имеем

∂ψ 1 dw А = Ж ∂H	∂H = д9 dw ∂ψ	∂ψ ∂θ = 5— = " ∂w ∂H	∂H ∂w - ∂θ , ∂ψ
следовательно,
∂w ∂ψ ∂ψ ∂θ ∂w ∂H	∂H ∂θ,	∂θ дф Эф = dw де = ∂H	∂H ∂w
Из последних	равенств, с учетом (2),			будем
иметь
Ф2 ( w ) дф w Ф 0 ( w ) дw	∂H -∂θ,	Ф ( w ) дф w 2 ∂θ	= дН ∂w.	(3)

Исключив из (3) напор Н, получим д / Ф2(w) Эф \

Эш w Ф 0 (w) Эш у ф(w) д2ф =

⁺ w ² Э 9 ²      ■

Итак, мы пришли к уравнению (4), которое линейно.

Наложим теперь условие

Ф² ( w )      w ²

w Ф 0 (w)    Ф (w) ’ откуда, сразу получаем

1 Ф ⁰ ( w ) w ³ Ф³ ( w )

Интегрируя это дифференциальное уравнение относительно Ф( w ), имеем

1     =   1

w ² + a Ф² ( w ) ’

a = const ,

откуда.

Ф ( w ) = w (1 + aw 2) , 1 / 2 a = const , 1 + aw ² >  0 . (C)

Из (6) мы получаем w2

Ф ( w )

= w (1 + aw 2)1 / 2

и, учитывая (5) и (7) из системы (3), будем иметь

(        )1 / 2 Эф     дН w (1+w  dw = - де, фФ (        )1 /2 дН дё = w (1 + aw) dw.

Если теперь ввести новую переменную

( w ) = ln----- , w =

(1 + V 1 + aw ²)

= In w — ln(1 + V 1 + aw ²) ,

TO r0 (w) = — — w

aw

(1 + V 1 + aw ²) V 1 + aw ²

w V 1 + aw ²

Так как

£=^ ( w ) • dH = ^ (w )

то, подставив последнее в систему (8), получим w (1 + aw2)1 /2 r0(w)= — |H, ∂r ∂θ

= w (1 + aw ²)1 / ² r⁰ ( w ) ^H .

∂θ                    ∂r

Принимая во внимание (9) и (10), из последних равенств имеем

∂ψ ∂H ∂ψ ∂H дё = dr, dr = — дё".

Таким образом, функция ф + iH является аналитической функцией комплексного переменного 9 + ir , ибо (11) — система Коши-Римана.

Закон (6) при a = — 1 /v ² известен как закон Соколовского. Но тогда, невозможны задачи с большими w , которые возникают, например, при моделировании фильтрационных течений к скважинам [2]. Поэтому для таких задач возможен закон (6) при a >  0. При a = 0 (6) является законом Дарси. Если a >  0. то можно положить a = 1 /v ² и назвать этот закон модифицированным законом Соколовского [3].

Рассмотрим фильтрацию несжимаемой жидкости к горизонтальной скважине в случае (6) при a >  0. Это плоское движение несжимаемой однофазной жидкости в пласте к горизонтальной скважине, расположенной в начале координат. Тогда, пласт — бесконечная горизонтальная полоса в плоскости ( x, у ) ширины 2 h с непроницаемой кровлей и подошвой (рис. 1). Горизонтальную скважину моделируем точечным стоком. Если рассмотреть точечный источник, то линии тока, останутся прежними, лишь векторы скорости, направленные по касательным к линиям тока, получат противоположные направления. Будем предполагать наличие в начале координат источника. Заметим, что реальные скважины имеют конечный диаметр, по т. к. характерные размеры пластов значительно превосходят характерные размеры диаметров скважин, то рассмотрение такой модели вполне оправдано.

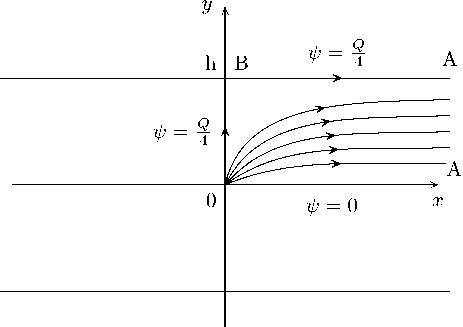
Рис. 1

Течение является симметричным относительно осей Ox и Oy (рис. 1). Достаточно построить решение задачи в первом квадранте, а. решения в остальных найдутся заменой знака, при соответствующих переменных.

Если принять, что полный расход через контур, охватывающий скважину и целиком лежащий внутри пласта, равен Q, то из стационарности течения получим, что на линии О А ф = 0, а на линии ОБА — ф = Q/ 4 (рис. 1).

Найдем, во что отображается рассматриваемая область при переходе к годографу. Новыми переменными будут 6 и w. Линия тока ОА, на которой ф = 0, в физической плоскости — положительная часть оси абсцисс (рис. 1) переходит в плоскости годографа, в часть оси ординат ОА (рис. 2). Часть линии тока ОВ, на которой ф = Q/ 4, в физической плоскости — это отрезок на положительной части оси ординат (рис. 1) переходит в вертикальный луч 6 = п/ 2, w >  0 (рис. 2). Часть линии тока В А, на которой ф = Q/ 4, в физической плоскости это луч y = h, x >  0 (рис. 1) переходит в вертикальный отрезок ВА на оси ординат (рис. 2). Заметим, что взаимная однозначность отображения нарушается в точке В физической плоскости. Она отображается на отрезок w = 0, 0 6 6 6 п/*2. Ордината, точки А в плоскости годографа легко находится из равенства: Q/ 4 = hw а, откуда w a = = Q/ (4 h )•

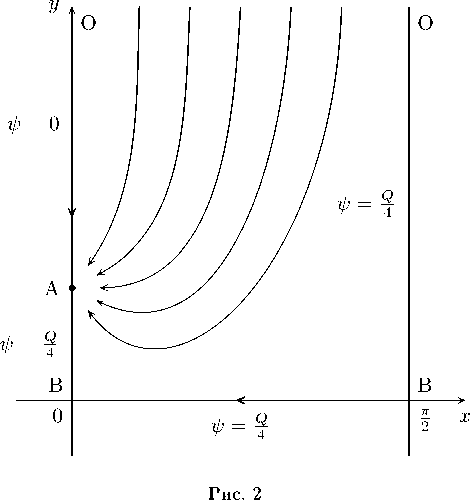
Таким образом, мы получили в плоскости годографа:

{ ( 6,w ): 0 6 6 6 -^ , 0 6 w< + го}.    (12)

Граничные условия, которым должна, удовлетворять функция тока, рассматриваемого течения, имеют вид (рис. 2):

ф ( 2,w )	Q 4 ’	w E [0 , + го ) ,
ф ( 6, 0)	= Q 4 ’	6 E [° -2 ] •	(13)
ф (0 , w )	Q 4 ’	w E [0 , w a ] ,
ф (0 , w )	= 0 ,	w E ( w a , + го ) .

При (9) полуполоса. (12) переходит в полуполосу

| ( 6,r ) : 0 6 6 6 п ,

го 2 in aj- (14)

(рис. 3). Действительно, из (9) видно, что при w го го +0 r го —го. а при w го + го r го — (in a ) / 2. Кроме того, из (10) следует монотонное возрастание (9).

r ф = ^ 2π ф = 0

θ ф = Q

A

ф = Q

B

B

Рис. 3

Граничные условия на. границе полуполосы (14) индуцируются формулами (13), за. исключением граничного условия на отрезке

{(⁶,^— 2^{in a} )^:0 6 ⁶ 6 1} .

Граничное условие на. (15) зададим таким, каким оно было бы в случае закона. Дарси. Поскольку [2, с. 33] функция тока, искомого течения для закона. Дарси в переменных годографа, имеет вид ф Q , IV1 — 2s cos 26 + s2 + 1 — s cos 26

D 2 п '    g у V 1 — 2 s cos 2 6 + s ² + s cos 2 6 — 1 ’

4 п 2 w 2        п s = Q2 m2 ’ m = 2h ’ то

*- = l™ *D = Q arctg          = Q⁹. (16)

s - + ^      2 п V 1 + cos 2 9   2 n

На основании (13), (15) и (16) можно определить граничные условия на ф в полуполосе (14):

ф = Q

ф(| ,r)

Q

4 ’

r ∈ -∞,

|ⁱⁿ a, ;

Ц⁶, - |^{Ь a} ) = Ц’ ^{9 Е} ['

ф (0 , r ) = 0 , r

∈

(- ^ a,

”Л rA ;

O          A B

ф(0,r) = Q , г Е (-го,га, ).

В формулах (17) r a = r ( w a), где правая часть определяется (9), т. е.

wA rA = ⁱⁿ 7-----/       \ =

(^^{1 +} v^{1 + aw}A)

Q

= ln ------- 4 h          . (18)

(^{1 +}V^{1 + a} ( Q ))

Рис. 4

В свою очередь из (11) и (14) заключаем, что

Для отыскания ф, удовлетворяющей уравнению (22) па. (23) и условиям (24), используем формулу 7.1. 1-8 [4, с. 416]: при 0 6 е < го , 0 6 9 6 6 П 2:

в области

A e,r ф = фёе + Ф"г = 0          (19)

ф ( е, 9 ) =

| ( 9, r ) : 0 < 9 <

π

2 ’

-∞ < r <

- in a 2

.

π

4 ^            2

= - 52 ^ехр( - 2 jе ) sin(2 j9 ) /

^π j =1                     ₀

f i( п ) sin(2 jn ) dn +

Введем теперь е = -г - 2 in a.(21)

Тогда из (19), (20) и (21) следует, что ф удов летворяет уравнению

A 5,9 ф = ф^ + ф^е = 0(22)

в области

{(е,г ):0<е< + го, 0 <9<П }.(23)

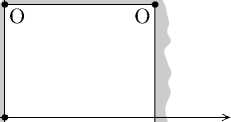
Из (17) и (21) следует, что ф удовлетворяет граничным условиям (см. рис. 4):

^ф (^ф I ) = ^Q ’ ^{е Е [0} ’ ^{+ ГО );}

ф (0 ,9 ) = £ , 9 Е [0 ,П ) ;

ф ( е, 0) = 0 , е е (0 ,С а ];

^{ф ( е}, ⁰⁾ = ^Q , ^{е Е ( е}А, ^{+ го} ) .

В формулах (24) е A = е ( r а ) ^гД^е правая часть определяется (21), т. е.

еА = -га - 2 in a.(25)

В свою очередь правая часть (25) определяется (18).

sin(2п9) Г J1

n J 1 ch[2( е — Z )] - cos 2 9

• ^-    ch[2( е + Z )] - cos 2 9 } f 2^{( Z} ) d^{Z +}

sin(2п9) Г J1

⁺ n J \ ch[2( е - Z )] + cos2 9

• -    ch[2( е + Z )] + co,2 9 }f 3^{( Z} ) d^Z- ⁽²⁶⁾

где fi( 9 ) = Q9/(2 n);

0 , f 2( е ) = | Q

⁰ < ^е< ^еА-еА <е<го-.

f 3 ( е ) = Q/ 4 .

Последние формулы получены из условий (24). Формула. (26) при (9) и (21) решает поставленную задачу. Однако (26) легко упростить. Действительно,

π

If i⁽ п )^sin(2 jn ) dn =

π

Q /n ^sin(2 jn ) dn = ^{Q ( -} 1) j.

2 n                  8 j

Поэтому

венства (30) получается связь между ( 6, w ) и ( x, у ):

Q ^ (-1) j ф (£,6) = V —•exp (-2 j£)sin (2 j6)+

2 п2-^   j j=1

Q sin(2 п6 ) 7(         1

^Ф    4 п    J [ch[2( £ — Z )] — cos 2 6

ξ A

sh2 mx =---1

2   2V1 — 2 s cos 2 6 + s ²

sin2 my = - +--,        s ,(3D

2   2 V1 — 2s cos 26 + s2' '

4 п ² w ²

^s Q 2 _m 2 ^.

ch[2( £ + Z )] — cos 2 6

j- d^Z +

Q sin(2 п6 ) 7(          1

^Ф    4 п    J ( ch[2( £ — Z )] + cos2 6

Из (30) напор и функция тока, в годографе имеют вид

V 1 — 2 s cos 2 6 + s ²

H d = — Q ln

ch[2( £ + Z )] + cos 2 6

j dZ- (27)

^фD =                                      (32)

V 1 — 2 s cos 2 6 + s ² + 1 — s cos 2 6

V 1 — 2 s cos 2 6 + s ² + s cos 2 6 — 1

= Q ^arctgv

Формула. (27) — окончательное выражение для функции тока, исходного течения при (6).

Степенной закона, фильтрации в годографе имеет вид

Ф( w ) = wn, n = const >  0 .        (28)

Функции (32) соответствуют пашей задаче с законом Дарси в плоскости годографа.

Вводится функция

Ф = ф — фD,              (33)

уравнение для которой получается из (29) и (33). Оно имеет вид

Случай n = 1 соответствует фильтрации по закону Дарси.

Уравнение (4) для степенного закона. (28) будет иметь вид

w ² д ²Ф д Ф д ²Ф n ∂w ^{2 w} ∂w ∂θ ²

Г w ² д ² ф_D    дф_D д ² ф_D 1

n ∂w ^{2 w} ∂w    ∂θ ^{2 .}

w ² д ² ф дф д ² ф о n ∂w ^{2 w} ∂w ∂θ ^{2 .}

Поскольку граничные условия при обоих законах фильтрации одинаковы, то в задаче для функции Ф граничные условия нулевые:

Обратимся в качестве примера, к задаче фильтрации несжимаемой жидкости к горизонтальной скважине при степенном законе (28). Мы рассматриваем плоское движение несжимаемой однофазной жидкости в пласте к горизонтальной скважине, которая расположена, в начале координат (рис. 1). Как и ранее, течение симметрично относительно осей Ox и Oy (рис. 1), и достаточно построить решение задачи в первом квадранте, а. решения в остальных найдутся заменой знака, при соответствующих переменных.

^Ф(2 ^,w ) =⁰ ,

Ф( 6, 0) = 0 ,

Ф(0 , w ) = 0 ,

Ф(0 , w ) = 0 ,

w Е [0 , + го );

^{6 Е} [⁰ Л ^];

w Е [0 , w a ]; w Е [ w_A, + го ) .

Сделаем преобразование независимой переменной и неизвестной функции, полагая w = exp {z/n ¹ / ² } 11 Ф( z,6 ) = exp[(1 — — n ) z/ (2 n ¹ / ²)]П( z,6 ):

w = exp

Течение в первом квадранте при преобразовании годографа, отображается в ту же замкнутую область (12), что и ранее (рис. 2), а. граничные условия, которым должна удовлетворять функция тока, по-прежнему даются формулами (13).

√ z _n

, Ф {z, 6 ) = exp

{Ы z } ⁿ( z,⁶ ) .

2 n

В случае закона. Дарси, следующего из (1) при Ф( w ) = w, искомое решение известно и имеет вид

[5]:

H d = — 4— In (sh² mx + sin² my ) , ф_D = arctg (cth mx tg my ) .

2 п

Тогда исходная полуполоса 6 Е ^{[0 ,п/} 2]. w ^Е

Е [0 , + го ) переходит в полосу 6 Е [0 ,п/ 2]. z Е

Е (—го, + го), а уравнение (34) примет вид д 2П   д 2П   (1 — n )2

az ^{2 +} д6 2    4 n    =

( n — 1 ) Г д ² ф_D

= ^{— exp} L^ Vnz J 7^5+ ⁺

+ ( Vn — Vn ) е + ^ 1 (36)

Здесь m = п/ (2 h ), г де h — половина толщины пласта, a Q — расход. На основании первых двух равенств (1) при Ф( w ) = w и первого ра

Фундаментальное решение однородного уравнения (36) в плоскости ( z,6 ) имеет вид [6]:

По( 6, z ) = K 0 (l ^ —n p z ² + 6 ² ) .

² v n

Здесь K 0 — функция Макдональда нулевого порядка. Чтобы найти решение в полосе 6 Е Е [0 , п/ 2], z Е ( го, + го ), нужно построить функцию Грина, для однородного уравнения Гельмгольца. После этого решение неоднородного уравнения (36) может быть найдено по второй формуле Грина. Значение в некоторой точке искомой функции представляется в формуле Грина, через фундаментальное решение, расположенное в этой точке. Таким образом, для построения функции источника, поместим источник в произвольной точке ( z, 6 ) и методом отражений относительно линий 6 = 0, 6 = п //2 добьемся того, чтобы на этих линиях функция источника, обращалась в поль. В результате приходим к бесконечной системе источников вида. [4]:

+ ∞

G ^{( w,6,}^n)   ., X

2π l = — ^

[к 0 f ^{1 1} n pn (ln w — ln £ )² + ( 6 — П — nl )² 2 n

I 1 — n|

K ⁰ ( 2 Vn

pn (In w — In £ )² + ( 6 + n + nl )²^ ,

ξ = exp

(P)

, w = exp

( VP

где n = 1.

Учитывая (33), получим следующее выражение для функции тока, течения жидкости при степенном законе фильтрации:

^{ф ( 6,w} ) = Q ^х

2 π

х arctg

I pl — 2 s 0 cos 2 6 + s 0 + 1 — s 0 cos 2 6 у pl — 2 s 0 cos 2 6 + s 0 + s 0 cos 2 6 — 1

Qw ^{1 -} 2 ⁿ

2 π

+ ^ п/ 2

G ( w, θ, ξ, η ) s sin 2 η (1 — 2 s cos 2 n + s 2) ^3-n

х

1+

1 — 3 s ² + 2 s cos 2 n

n (1 — 2 s cos 2 n + s 2)

s ₌ 4 π ² w ²

s ⁰     Q ² m ^{2 ,}

2(1 — s 2)

1 — 2 s cos 2 n + s ²

₌ 4 π ² ξ ²

Q ² m ^{2 .}

dη dξ,

Функция (38) при (37) является решением задачи (29), (13).

Итак, для (6) и (28) построены точные решения в плоскости годографа, для функции тока. Най

денная функция тока, связана, с напором уравнениями (3), что дает возможность найти частные производные напора по 6 и по w. Значит, нам известно поле градиента, напора.

Полученное решение можно интерпретировать как математическую модель притока, жидкости к горизонтальной скважине бесконечной длины. Опа может быть использована, для получения приближенного решения задачи о притоке к горизонтальной скважине большой протяженности [7]. Кроме того, полученное решение может быть применено к модели притока, к цепочке вертикальных скважин, которая имеет ту же математическую постановку, тем более что вблизи вертикальных скважин скорости обычно выше, чем вблизи горизонтальных, и нелинейные эффекты более существенны. В дальнейшем разработанную технику построения решения можно применить для исследования других областей течения, в частности, рассмотреть приток к разрезу конечной длины, что может соответствовать трещине гидроразрыва.