Нелинейная фильтрация к горизонтальной скважине в произвольной точке пласта в случае специальной нелинейности

Как известно, при больших скоростях движения жидкости не выполняется закон фильтрации Дарен в связи с проявлением инерционных сил [1] и для исследования фильтрации природных жидкостей к скважинам должны использоваться нелинейные законы.

В [2-4] рассматривался нелинейный закон, позволяющий упростить решение соответствующей краевой задачи в плоскости годографа, скорости, применимый в области больших скоростей:

Ф( w )

где w — скорость фильтрации w = | z w| . 1 /п — параметр. При стремлении параметра, закона, к нулю из выражения (1) получается закон Дарси, что позволяет контролировать правильность решения в нелинейном случае.

Подобный закон, но со знаком «—» в подкоренном выражении был ранее предложен В.В. Соколовским [5] для случая небольших скоростей фильтрации (вязкопластические жидкости).

В [3,4] показано, что только при законе (1) и при законе В.В. Соколовского уравнения в плоскости годографа, скорости сводятся к уравнению Лапласа.

В [2-4] было построено точное решение для случая симметричного расположения скважины относительно кровли п подошвы. Течение в этом случае симметрично относительно обеих осей координат, поэтому решение достаточно получить в первом квадранте плоскости.

Здесь так же, как и в [6, 7], рассмотрено точное решение этой задачи в общем случае, когда, скважина, расположена, в произвольной, необязательно симметричной относительно кровли и подошвы, точке пласта. Область решения в физической плоскости содержится в полуплоскости x > > x 0.

Прежде чем перейти к рассмотрению фильтрации при данном нелинейном законе, необходимо выполнить преобразование к переменным годографа. скорости.

Затем следует рассмотреть фильтрацию при законе Дарси в плоскости годографа, скорости. Необходимо получить связь между переменными годографа, скорости и переменными физической плоскости и получить выражения для функции тока, и напора, в новых переменных. Данные выражения используются для возможности сравнения результатов при линейном законе Дарси и рассматриваемом нелинейном законе фильтрации. К тому же выражение для функции тока, течения, подчиняющегося закону Дарси, необходимо для получения одного из граничных условий.

Перейдем к постановке задачи. Подзем ные жидкости часто залегают в пористых пластах, имеющих непроницаемую кровлю и подошву. Пласт рассматривается как бесконечная горизонтальная полоса в (x,y) высоты h (рис. 1). Непроницаемость кровли и подошвы пласта, означает равенство нулю вертикальной составляющей скорости фильтрации на. верхней п нижней границах пласта, (па. рис. 1 границы пласта, изображены пря-

‘Работа выполнена при поддержке Минобрнауки по гранту ВЦП РНПВШ 2.1.1 .№ 5904. Работа выполнена при финансовой поддержке АВЦП «Развитие научного потенциала высшей школы», протокол .№ 2.1.1/11133 и АВЦП «Развитие научного потенциала высшей школы», протокол .№ 2.1.1/12968.

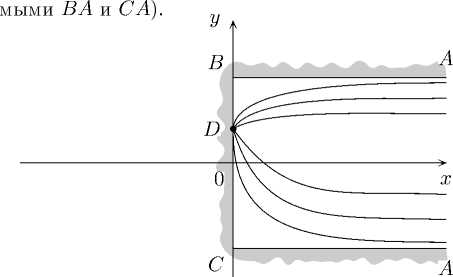
Рис. 1. Область течения в физической плоскости, отображение которой на плоскость годографа скорости выполняется в данной задаче

Рассматривается плоское движение несжимаемой однофазной жидкости в пласте к горизонтальной скважине (точечному стоку или источнику), которая расположена, несимметрично относительно кровли и подошвы (в точке D ( x 0 ,y 0)).

Система, уравнений, описывающих движение флюида, в пористой среде, имеет вид

Г - grad H = Ф( w ) w , ( div w = 0 ,

где H — иапор, Ф( w ) — закон фильтрации. Первое уравнение представляет собой связь между градиентом напора, и скоростью фильтрации [8], а. второе является уравнением неразрывности.

Вводится разрез плоскости, представляющий собой луч с началом в точке D (см. рис. 1), задаваемый уравнением: y = y 0, x < x 0, и достаточно отыскать функцию тока ф , такую, что равенства

∂ψ ∂ψ dx = -v,dy = u

Для начала, рассмотрим случай, когда, в постановке задачи используется закон фильтрации Дарен. Искомое решение для случая несимметричного расположения скважины относительно кровли и подошвы пласта, получено в работе [8], функция тока.

^ф = Q ^arctg

2 П

sin( my ) ch[ m ( x — x o)] — sin( my o) c°s( my ) sh[ m ( x — x ₀)]

}

при x > x o- y o E ( —h,h ). пде h — толщина, пласта. m = h Q — интенсивность источника.

Напор

H = — ln(sh²[ m ( x — x o)] c°s²( my )+

4 П

+(ch[ m ( x — x o)] sin( my ) — sin( my _o))²) .

Поскольку мы переходим в плоскость годографа, нужно выразить приведенные только что ф и H в переменных этой плоскости.

Получим частные производные воспользуемся соотношениями

∂ψ ∂ψ дх-ду- Затсм

справедливы вне этого разреза, и и v — компоненты вектора скорости фильтрации w по осям x и y соответственно.

Считая, что интенсивность источника равна Q, получим, что на линии DBA (рис. 1) ф = Q/ 4, на линии DC A ф = —Q/ 4.

Выполним преобразование годографа, в уравнении фильтрации природных жидкостей, подчиняющейся закону (1), которое позволяет свести уравнения в плоскости годографа, скорости к уравнению Лапласа.

Найдем, во что отображается область ABDCA при применении преобразования годографа. Новыми переменными будут ( 6, w ), г де 6 — угол между вектором скорости фильтрации в данной точке и положительным направлением оси x. К задачам фильтрации впервые это преобразование было применено С.А. Христиановичем в работе [9].

Область течения в переменных годографа скорости представлена, на. рис. 2. Переобозначим некоторые точки па. границах области, па. рис. 2 в скобках указаны новые обозначения.

w

∂ψ ∂x

—v,  д^ф = и, tg 6 = v,w ² = и ² + v ² .

∂y            u

Упростим получившиеся выражения и введем обозначения a = sin( my ), b = ch( m ( x — x o)). По

лучим следующую систему уравнений, которую необходимо разрешить относительно переменных

a. b:

^{(1 —} a ²⁾⁽ a ^— b ^sin( my o⁾⁾² = _tg2 ₆ ( b ² — 1)( b — a sin( my _o))²

( b ² — 1)( b—a sin( my o ))² + (1 —a ²)( a—b sin( my _o))² ( a ² + b ² — 1 — 2 ab sin( my o) + sin²( my o ))²

где s =

2πw

Qm '

Обозначим

— a sin( my _o))²

D

D ( F )      D ( D 1)

A

= s

( a — b sin( my _o))² = t. ( b —

= p. Тогда первое уравнение (3)

можно привести к виду

t + p ( s ² c°s²( my o) — 1) t p — t (1 + s ² c°s²( my o)) p

= tg² 6.

Введем новую переменную t/p = q. Получим квадратное уравнение с одной неизвестной, имеющее следующее решение:

q 1 , 2 = 2^(12 6 ( —s 2 c°s²( my o) +cos(2 6 ) ±

± p s ⁴ c°s⁴( my o) — 2 s ² c°s²( my _o) c°s(2 6 ) + 1 . (4)

C ( C 1)^™ ’ C I B’^B ( B 1)       6

Рис. 2. Область решения задачи в плоскости годографа скорости

Заметим, что взаимная однозначность отображения нарушается в точках B, C физической плоскости. Несложно найти выражение для ор-Q динаты точки A: wa = 2^.

Выразим отношение a/b через q ( 6,s ):

( a — b sin( my _o))² a   ±^S + sin( my o)

( b — a sin( my o))²    q, b    1 ± фд sin( my o)

Заметим, что при знаке «—» перед корнем в выражении (4) переменная q отрицательна. Величины же a, b , sin( my o) — по условиям задачи действительные.

Теперь можно выразить переменную a через b и найти решение системы (3). Таким образом, выра- жепие для функции тока, в переменных годографа, следующее:

Q         ab - sin( my o)

^ d =  arctg           =

^{2 п}      \V(1 - a ²)( b ² - 1)

= Q arctg [ T ( q,9 )] ,

2 П где

T(q,9)   tg 9 (1 - q) VQ cos2( my o) X x ((q + tg2 9 )(1 ± Vqi sin( my o))(sin( my o) ± Vq ) -

• - sin( my o)[ q (sin( my o) ± Vq )²+

+ tg² 9 (1 ± V q sin( my _o)²)]^ • (5)

Также приводим выражение для напора:

HD ⁼

= - — ln( a ² + b ² - 1 + sin²( my _o) - 2 ab sin( my o)) =

• 4 n

= -Q ln[ P ( q,9 )] ,

4 П

Заметим, что функция тока, заданная на. границе, терпит разрыв в точке

9 = 0 ,

ГА = ln

wA

¹⁺ FA

Обозначим z = 9 + ir. Уравнения (8) представляют собой условия Коши-Римана, следовательно, функция f = ф + iH является функцией одной переменной z.

Выполним ряд конформных преобразований, в результате которых область в плоскости z отображается па. верхнюю полуплоскость (рис. 3):

z 1 = z - i ln n, z2 = sin z 1, z3 = z2, z3 +sh2(га - ln n)           __ z 4 = ------------------, z 5 = - Vz 4 • z3

где

P ( q,9 ) = ( q + tg² 9 ) X

X

(1 ± Vq sin( my o))² + (sin( my o) ± Vq )²

.q (sin( my o) ± Vq )² + tg² 9 (1 ± Vq sin( my o))² 2(1 ± V q sin( my o))(sin( my o) ± Vq ) sin( my o) q (sin( my o) ± Vq )² + tg² 9 (1 ± Vq sin( my o))²

cos² ( my o)j ,

где q ( 9,s ) определяется выражением (4).

Рассмотрим случай использования нелинейного закона, фильтрации специального вида. (1). Система. (2) записывается следующим образом:

^dH 4 + 4)

∂x        n ²

V = (* + w ⁾

∂y        n ²

u,

v,

F D B, B 1 ^A    C, C 1 D 1

Рис. 3. Область решения в плоскости z ₅5

F θ 5

Граничные условия на отрезке DD 1 известны. Граничные условия на FD и D 1 F получим при помощи предельного перехода, в формуле (5), когда, скорость фильтрации стремится к бесконечности, т.е. в точке физической плоскости ( x o ,y o). В этом случае s также стремится к бесконечности. Применим правило Лопиталя для нахождения предела, и получим искомое значение, которое совпадает с предельным значением функции тока, в центральном случае расположения скважины:

Qθ ф^ = lim фD = s→∞     2 п

∂u ∂x

∂v

⁺ dy = •

В плоскости годографа, получаем из (6):

w (* + W )

2 _∂ψ

∂w

∂H ∂θ ,

∂ψ д9 = w

( 1+4)² H n ² ∂w

Мы получили граничное условие на. отрезках на. FD и D 1 F в области переменных ( 9,w ). Теперь найдем граничное условие на. части границы (лучи DF, D 1 F ) (рис. 3) в новых переменных и, таким образом, получим следующую постановку задачи Дирихле для функции тока, описывающей движение несжимаемой жидкости в окрестности горизонтальной скважины:

Сделаем замену переменных

в уравнениях (7)

так, чтобы избавиться от переменных коэффициентов:

r ( w ) = In---

1+

w

Fi

.

В новых переменных система. (7) приобретает

ВИД

∂ψ ∂H

∂r

∂θ

дф dH

∂θ ∂r .

А ф = 0 ,

Q             sh²( г а - ln n )

^ф|, 5=^o = 2 П ^arcsin          9 22 - 1    ^ ^ ,

9 6 G ( -го,   1 + sh²( г а - ln n )) ,

Ф 1 р 5=o = -Q, 9 2 G [ - У1 +sh²( г а - lln n ) , 0) , ^ф1Р 5=o = ^- ,   ⁹ 6 G ⁽⁰ , ^- q/1 ^{+ sh}2⁽ rA ^- ln n )) ,

Ф\р 5 = 0

Q

2 п

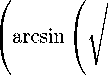
sh² ( г а — ln n ) 6 2 - ¹

ласти течения:

∂ψ ∂r 5

6 5 Е [v1 + sh²( г а - ln n ) , ж ) .

- 1

Q Г

2 п  J

-

-

1+ B ²

∞

arcsin( В/у/ n ² — ( n — 6 5)²

1) dn ₊

Обозначим В = sh( г а — In n ). Тогда решение задачи на. полуплоскости получится в виде

-^√ 1+ B ²

Q Г arcsin( В/s/n ² — 1) dn

2 п r ⁵ J     ( n — 6 5)² + г ^{2    +}

-∞

Ф ( 6 5 ,Г 5) = ¹ f

Q f dn Q f dn ⁺ 4 ^Г5 J ( n - 6 5)² + Г 2    4 ^TbJ ( n - 6 5)² + Г 2

• -√1+B20

∞

Q Г arcsin( В / л/n ² — 1) dn

2пT5 J        (n - 65)2 + Г2

^√ 1+ B ²

Выразим переменные ( 6 5 , г 5) через переменные ( 6, r ). Распишем подробнее выполненные конформные преобразования и получим выражение Для _________________________________ 6 5 = Т V1 / 2 + в ² G ( 6, г ) / (2 F ( 6, г )) + p A ( 6, г ) / 2 , где знак «—» при 6 >  0. знак «+» при 6 <  0. г 5 = — V — 1 / 2 — В ² G ( 6, г ) / (2 F ( 6, г )) + V A (M / 2 , где введены следующие обозначения:

G ( 6, г ) = sin² 6 ch²( г — ln n ) — sh²( г — In n ) cos² 6, F ( 6, г ) = (sin² 6 + sh²( г — In n ))² ,

A ( 6, г ) = 1 + (2 В ² G ( 6, г ) + В ⁴) /F ( 6, г ) .

Рассчитаем напор при нелинейном законе фильтрации (1). Значение напора, в произвольной точке области может быть выражено в виде криволинейного интеграла от величины dH по любой кривой, соединяющей эту точку и точку, удаленную от источника, где значение напора, можно считать равным значению при линейном законе фильтрации. Кривую, по которой производится интегрирование, выберем так, чтобы упростить подынтегральное выражение. Посчитаем напор по линии тока, совпадающей с границей области. Выберем границу области DBA (рис. 1). Возьмем точку w о на липии тока DBA на большом удалении от скважины (стока, или источника). Значение напора в точке w о можно положить равным значению напора, при законе Дарси.

Таким образом, интеграл сводится к интегралу Римана по отрезку оси w:

• п \ w 1 дф /п

H G ’w ) = / т (1 + т ² /n ²) д6 (2 ^,Т) d^T -w 0

Получим выражение для частной производной

Ig ( 6, w ) в области течения, для этого необходимо найти выражение для частной производной в об

+ Q /

dη

1+ B ²

( n

6 5 ) ²

1+ B ²

Q Z

dη

( n - 6 5)²

Q

2 п

∞ j

1+ B ²

arcsin( В/у/ n ² — ( n — 6 5)²

тХ . (10)

Теперь получим выражения для частных про-

∂θ ∂r изводных -г^ и |5 в области течения:

д6 5 = Т1 X д6 о I1 Л в2G(9,w)

² у 2 (^¹⁺ F ( 9,w ) ⁺ V A ^{( 6,w} )J

X

∂r 5 ∂θ

X

(

В 2( ^G ^ ^Tw ) F ( 6,w ) — ^F W w ) G ( 6,w ))

2 F ²( 6,w )              ⁺

²/I ( ^{— 1}

1      dA ( 6,w )!

⁺ 4p A ( 6, w ) d6 ,

--------------------x

BGW ¹+ ww))

В 2( ⁹G1I^TW ⁾ F ( 6, w ) — ^9Fd^Tw G ( 6, w ))

2 F ² ( 6,w )                ⁺

₊_____¹_____ ^{dA ( 6},w )     (12)

⁺ 4V A ( 6w )    д6 . ⁽⁾

Найдем предел подкоренного выражения в знаменателе выражения (11):

(1+ BFGBw ¹ + ж)

lim                            = е^п I                2                I

= ₁₊     в ²

ch²( г — ln n )

.

Предел подкоренного выражения в знаменателе выражения (12):

— 1 —

lim θ → ^π ₂

^Bn + ж 1 „ ---------Z--------------- — О .

Числитель выражений (11), (12) при 6 ^ п/ 2 — — 0 обращается в 0.

Найдем предел выражения ^ r при 6 ^ п/ 2 — 0. Раскроем неопределенность по правилу Лопиталя:

( «m    Y

θ → π/ 2 - 0 ∂θ

= lim θ → π/ 2 - 0

1 В ²

‘ д ² G ( 6,w )

4 F ²( 6, w )

д ² F ( 6,w )        1

d6 2    G ^{( 6},^w ) ⁺

∂θ ²

∂ ²

F ( 6, w ) —

2 v A w w )

A6w ). (13)

Теперь, пользуясь полученными выражениями (9), (10), (11), (12), (13), можем построить качественный график напора, при нелинейном законе фильтрации.

Сравним графики напора, при нелинейном законе фильтрации для вертикальной скважины (источника. или стока.) и для горизонтальной скважины (источника, или стока, в полосе). Несложно рассчитать напор для нелинейного закона, фильтрации (1) для стока, (источника) для того, чтобы сравнить результаты, полученные для более простой модели стока, (источника), с результатом, полученным для модели горизонтальной скважины в полосе:

H = -C i ln--+ \ —т; +—у + C 2 .    (14)

w w ²    n ²

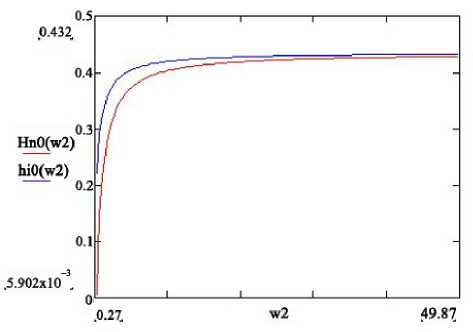
Рис. 4. Графики напора для горизонтальной сква жины Hn 0( w 2 ) 11 вертикальной скважины hi 0( w 2). Q = 1: h = 150: n = 1: w 6 ( w a ; 100): C 1 = Q/ 4 n: C 2 = 0 , 38