Нелинейная эволюция и взаимодействие частотно-модулированных импульсов различной формы в одномодовом оптическом волокне

НЕЛИНЕЙНАЯ ЭВОЛЮЦИЯ И ВЗАИМОДЕЙСТВИЕ ЧАСТОТНО-МОДУЛИРОВАННЫХ ИМПУЛЬСОВ РАЗЛИЧНОЙ ФОРМЫ В ОДНОМОДОВОМ ОПТИЧЕСКОМ ВОЛОКНЕ

Использование сверхкоротких импульсов позволяет существенно повысить скорость передачи информации по оптическим волокнам за счет взаимной компенсации нелинейных и дисперсионных эффектов. Первыми для системы связи были предложены солитоны [1,2]. Однако существует еще целый класс форм импульсов, слабо уширяющихся в процессе распространения по волокну на небольшие расстояния [3] . Динамика некоторых таких импульсов в нелинейных диспергирующих средах (каковой является оптическое волокно для сверхкоротких импульсов) рассматривалась в [4,5]. Методом численного моделирования там проанализирована эволюция импульсов кнои-дальной, гауссовской и параболической формы при отсутствии начальной модуляции частоты. Однако такая модуляция, в частности линейная (ЛЧМ), существенно влияет на характер динамики, позволяя существенно сжимать и расширять импульс на начальном участке эволюции.

Эволюция нормированной огибающей ф(л, т) интенсивного короткого импульса по продольной координате в одномодовом оптическом волокне с пренебрежимо малым затуханием описывается нелинейным уравнением Шредингера (НУШ), которое в нормированной записи имеет вид [3.5]

^ + Й + м I Ф I 2Ф = 0(1 )

ЭИ df2 с начальным условием ф(0, т) = ф0(т), определяемым импульсом в начале эволюции (на входе волокна) .

Для начального импульса с ЛЧМ поведение решения НУШ (1) можно аналитически исследовать в рамках а втомодельного подхода, при котором решение ищется в виде !т2                   т21

--—--- + is (л) — + 1<р(п) •                          (2) 2T=f2(n)          2J

В линейном случае (при и = 0) такой подход позволяет получить точное решение. Вариационный метод решения задачи (1), (2) [6] дает значения параметров модели (2) в виде обыкновенных дифференциальных уравнений.

f

s

= J_ (J- f-3 - 2L f"2);

T2 v2

= — (— f ~ D , f2 2/2

где f = — f =      , f(0) = 1, f(0) = 2s(0).

dn dn

И хотя (3), W качественно правильно отражают эволюцию пика интенсивности и ширины импульса, точность такого подхода, как видно по рис. 1а, б, невелика.

На рис. 2 показаны зависимости от параметра нелинейности х максимальной относительной погрешности (в процентах) для пика интенсивности, рассчитанного по (3), (М, по сравнению с непосредственным численным решением (1) для входного импуль-

IФI

а max

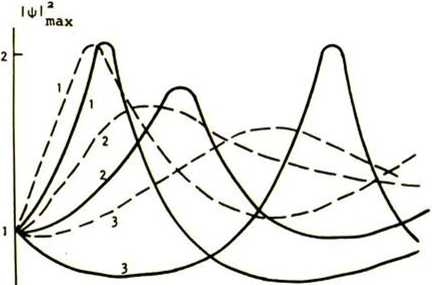
Рис. 1. Эволюция максимума интенсивности частотно-модулированного импульса ф0 (т) = ехр(-т2/2 + is0T2/2) в рамках автомодельного (— - -) и непосредственного численного (-----)

решения НУШ при х=2 (а) и х=4 (б) для so=-0,5 (1), so=0 (2), so=0,5 (3)

б

• 6,    t

50 -

1.0 -                                    /

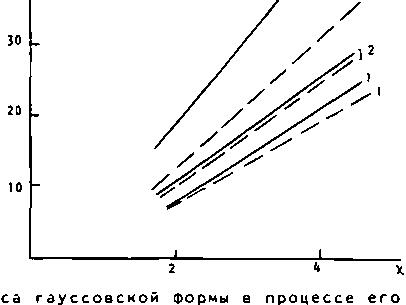
Рис. 2. Зависимость максимальной относительной погрешности б,% от нелинейности х при расчете эволюции пика интенсивности гауссовского импульса фо(т) = ехр(-т2/2 + is т2/2) на расстояния п=0,5(— - -) и п=1(------)

для s =-0,5 (1), so=0 (2) и so=0,5 (3)

олюции на расстояние и = 0,5 и и = 1 при некоторых значениях параметра ЛЧМ so = s(0). Видно, что с ростом х погрешность автомодельного подхода быстро возрастает и даже при х» 2 точность этого подхода недостаточна для получения численных оценок. Величина и знак начальной ЛЧМ существенно влияют на точность автомодельного решения (2).

Таким образом, для исследования эволюции и тем более - взаимодействия несолитонных импульсов в рамках шредингеровской модели (1) пока остается единственный способ - численное решение непосредственно НУШ (1).

На рис. 3 изображена динамика максимума интенсивности для начального импульса ф0(т) = ехр(- т/2 + isQT2/2). В асимптотике при больших ц его значение не зависит от начальной величины ЛЧМ s0, а форма импульса приближается к солитонной, соответствующей энергии начального импульса.

В отсутствие ЛЧМ (при so = 0) с увеличением параметра х бесколебательная эволюция сменяется колебательной при х = 4х , кр’

Ккр = 2" |/*o(r)dr|'2 = 5

max

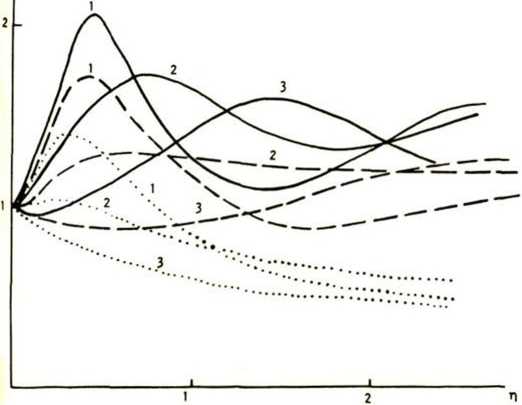
Рис. 3. Динамика пика интенсивности частотно-модулированного гауссовского импульса ф0(т) = ехр(-т2/2 + is0T2/2) при х=2 (......), х=п (- - -) и х=4 (------)

для so=-0,5 (1), s0=C (2) и so=0,5 (3)

как и для импульсов с параболической огибающей [$]• Увеличение параметра и приводит к увеличению амплитуды колебаний пика интенсивности.

Рост |s₀ I переводит режим эволюции в колебательный с увеличением амплитуды и периода. Кроме того, следует отметить, что уменьшение параметра ЛЧМ s_q (с уче том знака) ускоряет перестройку импульса.

Рассмотрим сравнительную эволюцию частотно-модулированных импульсов различной начальной формы: се кан с - гиперболической (солитонной), гауссовской и параболической при одинаковом значении параметра и = 5 (одинаковой пиковой мощности). В силу особой значимости режима и = ^икр начальную ширину импульса в каждом случае выберем, чтобы последнее соотношение удовлетворялось при s0 = 0 (см. рис. А). Видно, что импульсы с большей степенью локализации энергии перестраиваются быстрее и имеют большую частоту в колебательной эволюции. Величина ЛЧМ примерно в одинаковой степени влияет на динамику импульсов, независимо от их формы.

Поскольку наличие частотной модуляции приводит к колебательной эволюции импульса относительно "положения равновесия", определяемом случаем sQ = 0, то лишь отрицательная ЛЧМ может привести к увеличению различимости (соответственно

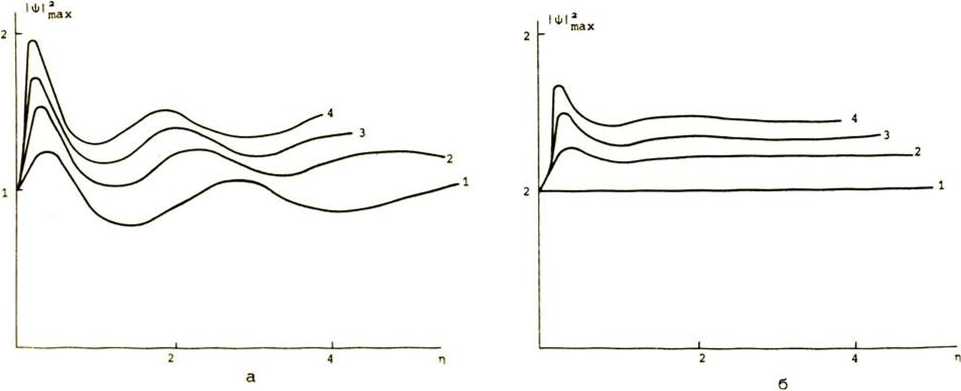
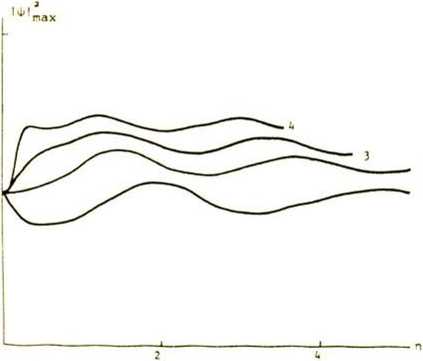
Рис. 4. Сравнительная эволюция частотно-модулированных импульсов разной формы

(Фо(т) = 5есЬ(У^) exp(is0 ^ (1),

Фо(т) = ехр(-та/2та ♦ is0Ta/2) (2), Ф0(т) = [1 - (т/та) z]^2 ехр( i $ота/2) , v=2 (3) и v=5 (4)) при х=5 и s0=—0,5 (а), so=O (б),   so=0,5 (в).

Начальная длительность т₀ для каждого из импульсов удовлетворяет соотношению и = 4x_Kpo=0)

к росту дальности различимой передачи [4]) при передаче одинаково модулированных импульсов (и то лишь на коротких расстояниях), определяемых половиной "периода" колебаний.

Однако "встречная" модуляция соседних импульсов в случае, когда их колебательная эволюция происходит в противофазе, способна замедлить скорость взаимодействия импульсов, тем самым увеличивая дальность различимой передачи. Эта возможность иллюстрируется рис. 5, где изображены картины эволюции двух взаимодействующих импульсов гауссовской формы

Ф_о(т) = ехр[- ^{(т +}/— + is, ^(т V^T— J ⁺

+ ехр[- (т ' Дт)2 + is (т " Лт)2 1 2               2        2 J в отсутствии начальной ЛЧМ (а), при одинаковой ЛЧМ обоих импульсов (б) и при "встречной" ЛЧМ (в), когда параметры s, и sa подобраны так, чтобы обеспечить противофазную эволюцию этих импульсов.

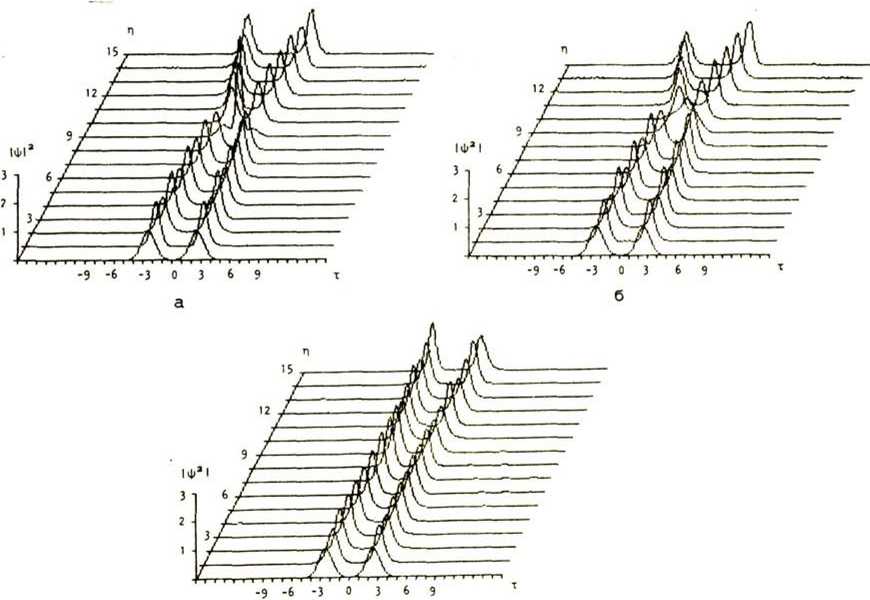
Рис. 5. Влияние начальной ЛЧМ на взаимодействие гауссовских импульсов в одномодовом оптическом волокне при х=4 и Дт=2,5. s1=sa=0 (a); s1=sa=-0,3 (б); Si=0,5, sa=-0,3 (в)