Нелинейная эволюция импульсов различной формы в волоконном световоде

НЕЛИНЕЙНАЯ ЭВОЛЮЦИЯ ИМПУЛЬСОВ РАЗЛИЧНОЙ ФОРМЫ В ВОЛОКОННОМ СВЕТОВОДЕ

Процессы контролируемой нелинейной эволюции интенсивных сверхкоротких импульсов в волоконных световодах привлекают в последние годы большое внимание в связи с возможностями их использования для передачи цифровых сигналов с особо высокими скоростями [1, 2]. Эволюция нормирован- ной комплексной огибающей ф(п, т) локализованного волнового поля в оптическом волокне с кубической характеристикой поляризации и пренебрежимо малым затуханием (без учета дисперсии выше второго порядка и ряда второстепенных нелинейных явлении, связанных с зависимостью групповой скорости от интенсивности, генерацией гармоник и т.п.) описывается нелинейным уравнением Шредингера.

1 ^ + Й + х1ф|2ф = 0                                    (1)

с начальным условием ф(0, т)=Фо(т), определяемым импульсом на входе световода, где х ~ параметр нелинейности, зависящий от свойств среды и мощности входного импульса (знак + соответствует аномальной дисперсии), П, т - нормированные координаты, связанные с продольной пространственной координатой z и реальным временем t соотношениями

П = z/L0, т = (t-z/vo)/To.

Здесь v_q - групповая скорость, L_o, Т_о - характерные масштабы (например, "дисперсионная длина" и полуширина начального импульса) [2].

Наряду с известными решениями нелинейного уравнения Шредингера в виде одного или нескольких солитонов с огибающей |ф(п, т) I 2=ch~2 (\/х/2т) возможны и многие другие режимы стабилизации импульсов, отличающиеся от солитонных большим числом степеней свободы и потому в ряде случаев более предпочтительные для передачи информации [2]. Особый интерес представляют процессы передачи импульсов в форме усеченных эллиптических косинусов, так как функция вида

Ф(П, т) = сп(т/Д, к)е^ап                                         (2)

является стационарным решением нелинейного уравнения Шредингера [з]. Параметры в нем связаны соотношениями

Д =         а = Х(1 _ _1_).                                         (3)

Выражение (2) задает семейство огибающих, зависящее от параметра 0<к$1, причем значению к=1 соответствует солитон.

Переход к усеченной функции связан с необходимостью формирования Финитных импульсов, используемых для передачи цифровых сигналов.

Гсп(т/т0 , k), IтISK ф0(т) = У о , | т IЖ , где К - четверть периода.

В отличие от периодического колебания (2) импульс (4), конечно, уже не является решением нелинейного уравнения Шредингера (1) и его Форма при передаче по световоду не сохраняется. Ниже рассматриваются результаты анализа эволюции импульсов вида 4), полученные методом цифрового моделирования.

На рис. 1а, б показано изменение максимума интенсивности импульса ^(П, 0) |2 вдоль волокна в зависимости от х- Как и в других аналогичных задачах [21, здесь можно выделить некритический и закритический режимы

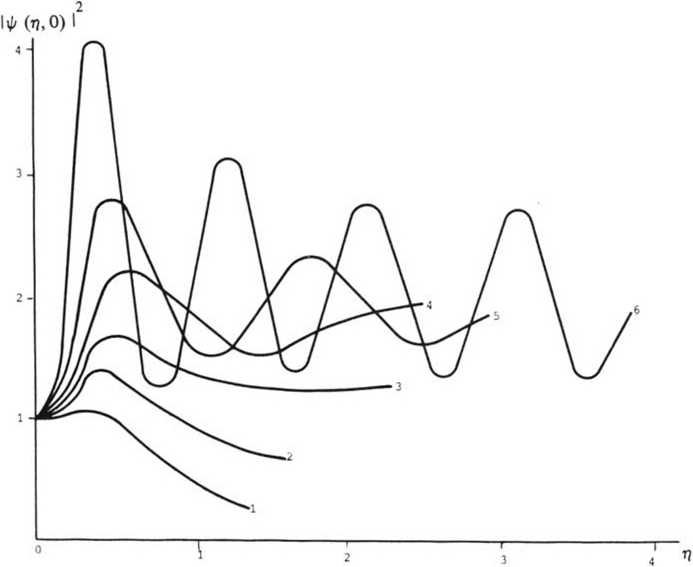
Рис. la

При к=0,1: 1 - х=0,1; 2 - х=2; 3 - х=3; 4 - х=4; 5 - х=6; 6 - х=7

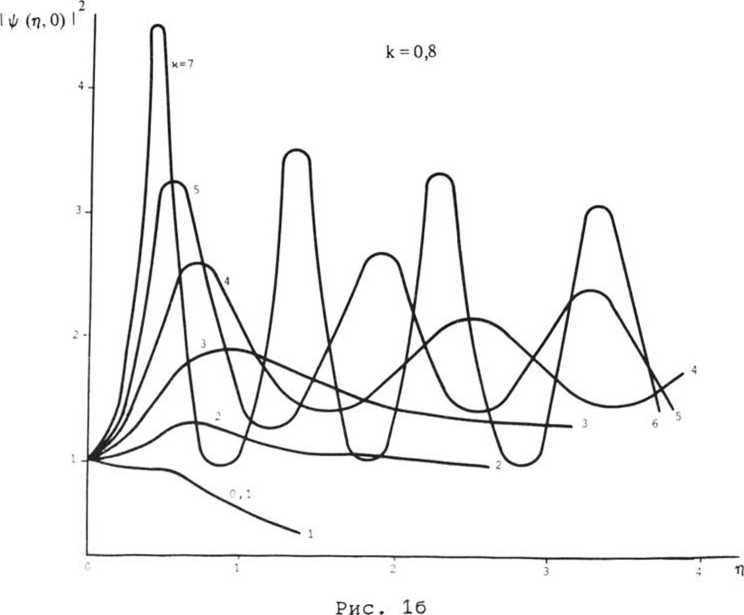
При к=0,8; 1 - х=0,1; 2 - х=2; 3 - х=3; 4 - х=4; 5 - Х=5; 6 - Х=7

- НО -

эволюции. В докритическом режиме (х<Х ) величина |ф| 2 после слабого Кр возрастания монотонно убывает с ростом г), а в слабозакритическом режи ме (х^х„_

Кр значению.

максимум интенсивности импульса стремится к стационарному

При дальнейшем увеличении мощности входного импульса |ф|2

эволюционирует по колебательному закону, стремясь на бесконечности к стационарному значению тем большему, чем больше параметр нелинейности X* С увеличением х период колебаний уменьшается. Ширина импульса изменяется обратно пропорционально максимуму интенсивности.

Из сравнения рисунков 1а и 16 видно, что увеличение параметра к, определяющего начальную форму импульса, приводит к уменьшению х , кр увеличению периода и амплитуды колебаний максимума интенсивности.

Для оценки максимально достижимой скорости передачи цифровых сигналов по рассматриваемому нелинейному волоконно-оптическому каналу было исследовано взаимодействие двух импульсов вида Фо (т) =сп (^—^^, к) + + cn^t^, к).

То

На рис. 2 изображены графики предельной нормированной длины световода г)р, при которой еще сохраняется возможность различения указанных импульсов, в зависимости от интервала Дт для разных значений параметров нелинейности х и формы импульса к. Неоднозначность функции пр(Дт) при больших значениях х свидетельствует о том, что при большой нелинейности первоначально "неразличимые" импульсы в процессе эволюции сжимаются настолько, что становятся различимыми. Последующее расширение им пульсов и их взаимодействие друг с другом приводят к потере различи мости.

Полученные кривые позволяют определить максимальную частоту следования импульсов на входе световода, допускающую их раздельный прием на выходе. Например, при передаче сообщений на расстояние одной дисперсионной длины сигналами начальной формы, соответствующей к=0,8, требуется их разнесение на 5,75 полуширины при х=0,1 и на 3,6 полуширины при х=2. Минимально допустимый интервал между импульсами при фиксированных значениях параметров х, к является некоторой функцией длины световода Дт . =f(п) . min

При условии независимости отсчетов сигнала и пренебрежимо малых помех достижима передача информации со скоростью ( в бит/с),

I' (П) = log2m/Tof (п), где m - основание кода. Реально ш, конечно, не может быть сколь угодно большим, его значение (а вместе с ним и I') подчиняется ограничениям, обусловленным действием шума и устанавливаемым теорией информации. За счет уменьшения То также нельзя неограниченно увеличивать I1, т.е. при этом растет f (п) .

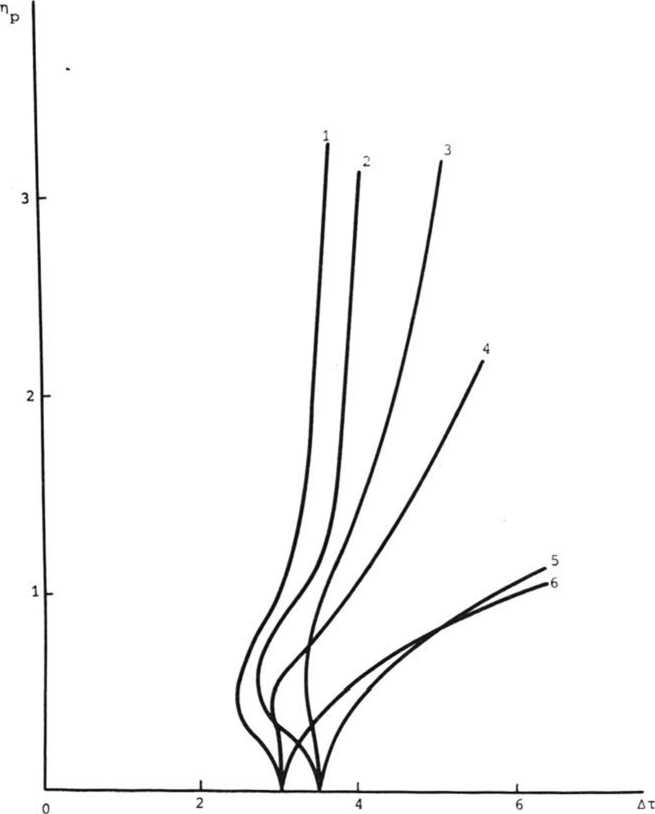
Рис. 2

1 - х=5, к-0,1; 2 - х=5, 5 - Х=0,1,

к=0,8; 3 - х=2, к=0,8; 4 - х=2, к=0,8; 6 - х=0,1, к=0,1

к= 0,1;

На рис. 3 представлены зависимости нормированной скорости 1|,Т от параметра нелинейности х при использовании двоичных сигналов (т=2) для различных значений длины световода г) и параметра формы сигнала к. Из приведенных графиков видно, что при прочих равных увеличение вводимой в световод мощности позволяет повысить возможную скорость передачи сообщений .

Чем короче дальность передачи п, тем меньшие значения к предпочтительно выбирать для достижения максимальной скорости. На больших расстояниях оптимальными в этом смысле являются солитонные импульсы, соот ветствующие к=1.

I ' -To

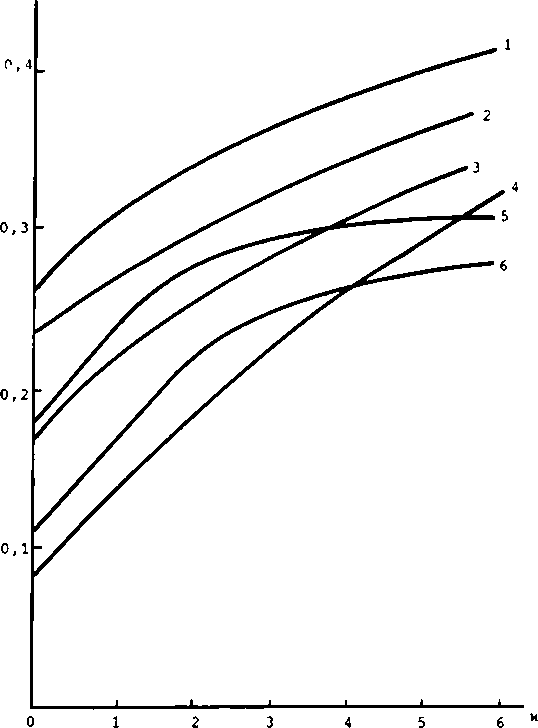
Рис. 3

1 - k=0,l, n=0,5; 2 - k=0,8, n=0,5; 3 - k=0,1, n=l i 4 - k=0,l, n=2> 5 - k=0,8, n = l; 6 - k=0,8, n=2