Нелинейная эволюционная задача для самонапряженных слоистых гиперупругих сферических тел
Автор: Лычев С.А., Лычва Т.Н., Койфман К.Г.
Статья в выпуске: 1, 2020 года.
Бесплатный доступ
В работе исследуется эволюционная задача для самонапряженных слоистых полых шаров. Их напряженно-деформированное состояние характеризуется несовместными локальными конечными деформациями, возникающими из-за геометрической несогласованности ненапряженных форм отдельных слоев друг с другом. В рассматриваемой задаче эти формы представляют собой тонкостенные полые шары, которые не могут быть собраны в единое сплошное тело без зазоров или пересечений. Подобная сборка возможна только при предварительной деформации отдельных слоев, что и вызывает самоуравновешенные усилия в них. Для слоистых структур с большим количеством слоев предлагается процедура континуализации, в результате которой кусочно-непрерывные функции, определяющие предварительную деформацию слоев, заменяются непрерывными распределениями. Отсчетная ненапряженная форма построенного таким образом тела определяется в рамках геометрической механики континуума как многообразие с неевклидовой (материальной) связностью. Для рассматриваемой задачи эта связность определяется метрическим тензором, и ее отличие от евклидовой характеризуется скалярной кривизной. Методами геометрической механики континуума могут быть определены обобщенные представления для напряжений Коши и Пиолы. Вычисления, проводимые для дискретной структуры и тела с неевклидовой отсчетной формой, определяемой аппроксимацией параметров деформации, численно иллюстрируют сходимость решений дискретной модели с непрерывной при увеличении числа слоев с неизменной суммарной их толщиной. В расчетной модели предварительно напряженного слоистого полого шара и его континуального аналога предполагается, что материал слоев - сжимаемый, гиперупругий, однородный, определяемый упругим потенциалом Муни - Ривлина первого порядка. Индивидуальные конечные деформации слоев являются центральносимметричными.
Несовместные деформации, остаточные напряжения, слоистые тела, неевклидова отсчетная форма, материальная связность
Короткий адрес: https://sciup.org/146282059
IDR: 146282059 | УДК: 539.3 | DOI: 10.15593/perm.mech/2020.1.04
The nonlinear evolutionary problem for self-stressed multilayered hyperelastic spherical bodies
The present paper studies the evolutionary problem for self-stressed multilayered spherical shells. Their stress-strain state is characterized by incompatible local finite deformations that arise due to the geometric incompatibility of the stress-free shapes of the individual layers with each other. In the considered problem, these shapes are thin-walled hollow balls that cannot be assembled into a single solid without gaps or overlaps. Such an assembly is possible only with the preliminary deformations of individual layers, which cause self-balanced stresses in them. For multilayered structures with a large number of layers, a smoothing procedure is proposed, as a result of which the piecewise continuous functions defining the preliminary deformation of the layers are replaced by continuous distributions. The reference stress-free shape of a body constructed in this way is defined within the framework of geometric continuum mechanics as a manifold with a non-Euclidean (material) connection. For the problem in question, this connection is determined by the metric tensor and its deviation from the Euclidean connection is characterized by the scalar curvature. Generalized representations for Cauchy and Piola stresses are also obtained by the methods of geometric continuum mechanics. Computations, provided for the discrete structure and body with a non-Euclidean reference shape defined by the approximation of deformation parameters, numerically illustrate the convergency of the solution for the discrete model to corresponded solution for the continuous problem if the number of layers is increasing while their total thickness is constant. In modelling it is assumed that the material of the layers is compressible, homogeneous, hyperelastic, and determined by the first-order Mooney - Rivlin elastic potential. Individual layerwise finite deformations are supposed to be centrally symmetric.
Текст научной статьи Нелинейная эволюционная задача для самонапряженных слоистых гиперупругих сферических тел
The present paper studies the evolutionary problem for self-stressed multilayered spherical shells. Their stress-strain state is characterized by incompatible local finite deformations that arise due to the geometric incompatibility of the stress-free shapes of the individual layers with each other. In the considered problem, these shapes are thin-walled hollow balls that cannot be assembled into a single solid without gaps or overlaps. Such an assembly is possible only with the preliminary deformations of individual layers, which cause self-balanced stresses in them.
For multilayered structures with a large number of layers, a smoothing procedure is proposed, as a result of which the piecewise continuous functions defining the preliminary deformation of the layers are replaced by continuous distributions. The reference stress-free shape of a body constructed in this way is defined within the framework of geometric continuum mechanics as a manifold with a non-Euclidean (material) connection. For the problem in question, this connection is determined by the metric tensor and its deviation from the Euclidean connection is characterized by the scalar curvature. Generalized representations for Cauchy and Piola stresses are also obtained by the methods of geometric continuum mechanics. Computations, provided for the discrete structure and body with a non-Euclidean reference shape defined by the approximation of deformation parameters, numerically illustrate the convergency of the solution for the discrete model to corresponded solution for the continuous problem if the number of layers is increasing while their total thickness is constant.
In modelling it is assumed that the material of the layers is compressible, homogeneous, hyperelastic, and determined by the first-order Mooney - Rivlin elastic potential. Individual layerwise finite deformations are supposed to be centrally symmetric.
-
1о. В настоящее время интенсивно развиваются технологии, позволяющие создавать слоистые структуры микронного масштаба с предварительно напряженными (самонапряженными) слоями. Такие структуры используются, например, для изготовления сферических микрокапсул, транспортирующих химические вещества в биосистемах [1–7]. Как правило, предварительные напряжения являются неизбежными нежелательными факторами и возникают вследствие физико-химических процессов, протекающих при создании или присоединении слоев. К ним, в частности, относятся: локальный нагрев при эпитаксиальном осаждении [8, 9], перераспределение ионных и вандерваальсовых связей на поверхностях соединяемых тонких пленок при LbL-процессинге [10, 11] и молекулярных агрегатов при са-моассемблировании [12], усадки в результате фотохимической солидификации в ходе стереолитографии [13] и пр. Однако в некоторых случаях предварительные напряжения могут быть созданы намеренно для придания желаемой неоднородности и анизотропии материалам слоев. Ярким примером является технология Strained Silicon , позволяющая за счет деформирования тонкого кремниевого слоя на подложке создать заданную анизотропию проводимости. В результате тепловые потери вентилей снижаются и появляется возмож-
- ность увеличить их плотность на кристалле [14]. Таким образом, помимо задачи моделирования, практически важными оказываются задачи оптимизации предварительно напряженных слоистых структур относительно целевой функции, характеризующей приближение к желаемому распределению внутренних напряжений в теле.
При постановке перечисленных выше задач, как правило, предполагается, что: 1) деформации не могут считаться малыми; 2) для всей структуры в целом отсутствует свободная от напряжений отсчетная форма; 3) число слоев может быть очень велико. Математические методы моделирования механики и физики твердого тела, учитывающие эти факторы, далеки от завершения и представляют собой интенсивно развивающуюся область нелинейной механики континуума [15–20].
Поиск свободной от напряжений отсчетной формы для всей слоистой структуры в целом приводит к идее о погружении тела в пространство, геометрические свойства которого более общие, чем у евклидова. Это позволяет, используя дополнительные геометрические параметры, совместить без зазоров и наложений слои, не создавая в них напряжений. При этом параметры будут иметь конечные разрывы на границах слоев, но при большом количестве слоев они, согласно принятой в механике сплошной среды идее континуализации, могут быть аппроксимированы непрерывными функциями. В результате слоистой структуре ставится в соот- ветствие гладкое тело (в смысле Нолла, [21]), отсчетная ненапряженная форма которого определяется в пространстве с неевклидовой непрерывной (аффинной) связностью. Эта связность называется материальной [15, 21], а определенное таким образом гладкое тело – неевклидовым телом, которое эквивалентно некоторому телу с непрерывно распределенными дефектами [22].
Эффективность геометрического подхода показана во многих работах [22–30]. Вместе с тем континуализа-ция слоев, т.е. переход от дискретной слоистой структуры к непрерывной, может быть осуществлен различными способами, и вопросы об их строгом обосновании пока остаются открытыми. По этой причине сопоставление конкретных задач с дискретной структурой и соответствующих им непрерывных задач имеет как прикладной, так и теоретический интерес.
Настоящая работа продолжает серию статей, в которых рассматриваются модельные задачи об определении напряженно-деформированного состояния многослойных структур при конечных деформациях и различных условиях нагружения [31–34]. Используются идеи, развитые в теории тел переменного материального состава (растущих тел) [20, 35, 36]. В отличие от предшествующих работ, впервые рассматривается случай сжимаемого гиперупругого материала. Цель настоящей работы – исследование модельной нелинейной задачи для самонапряженного слоистого полого шара, его континуализованного аналога и сопоставление результатов вычислительного моделирования.
-
2o. В начале работы приведем некоторые общие определения.
Под телом [21] (гладким телом) B будем понимать континуальное множество материальных точек, снабженное структурой гладкого трехмерного многообразия [37]. Под конфигурацией понимается гладкое вложение х : B ^5 [37] тела B в физическое пространство 8 , которое, в свою очередь, является гладким трехмерным многообразием. Образ конфигурации, x(B) , представляет собой точечное множество в физическом пространстве – форму тела.
Одно и то же тело может иметь сколь угодно много форм. Композиция1
Y = -': ^ (B) >.(B| двух конфигураций, , , определяет деформацию – отображение одной формы, xR (B), на другую, x(B) .
Среди всех форм выделяются особые – натуральные – формы, свободные от напряжений.
Тело может быть результатом соединения некоторого конечного количества слоев. В этом случае тело будем называть сборкой (из указанных слоев). Сборка, в общем случае, не имеет натуральной формы, но каждый из слоев в отдельности – имеет.
Работа имеет следующую структуру. В первом разделе исследуется задача о центрально-симметричных деформациях сборки из конечного числа тонкостенных полых шаровых слоев. Натуральные формы слоев геометрически несовместны: любое их соединение без деформации имеет либо зазоры, либо наложения. Величины этих зазоров или наложений определяются рекур-рентно из эволюционной задачи, моделирующей технологический процесс. Аналитическое решение нелинейной краевой задачи для несжимаемого гиперупругого материала слоев (предполагается, что отклик определяется двухконстантным потенциалом Муни – Ривлина) построено в подразд. 1.4. Решение представлено в виде конечных алгебраических выражений, которые содержат корни трансцендентных уравнений, определяемых численно. Начальные приближения для них определяются из решений линейной задачи. В подразд. 1.5 нелинейная задача для сжимаемого материала, отклик которого определяется трехконстантным потенциалом Муни – Ривлина, приводится к системе обыкновенных квазилинейных уравнений и соответствующей двухточечной краевой задаче. Она решается методом пристрелки, в котором начальные значения искомых функций и их производных определяются из задачи для несжимаемого материала. Математически свойство самонапряжен-ности выражается тем, что в отсутствие внешних силовых полей меры деформаций (более точно – локальных деформаций из ненапряженного состояния) отличны от нуля и определены кусочно-непрерывными функциями с разрывами на границе слоев. Вычисления, приведенные в подразд. 1.5, показывают, что при уменьшении толщины слоя и увеличении их числа величины разрывов уменьшаются. Это наблюдение подсказывает идею аппроксимации компонентов мер деформаций непрерывными функциями. В результате такой аппроксимации тело становится неевклидовым и приобретает новую физическую характеристику – меру несовместности локальных деформаций, или, в терминах континуальной теории дефектов, плотность дефектов. Вычислительное сопоставление слоистых структур и соответствующих им неевклидовых тел при различном числе слоев приведено в подразд. 2.
-
1. Эволюция дискретной структуры
-
1.1. Тела-слои и тела-сборки
-
-
3o . Рассмотрим сборки, состоящие из конечного числа шаровых слоев. Полагаем, что для каждого слоя в отдельности существует конфигурация, образ которой –
форма слоя - свободен от напряжений. В общем случае эти формы геометрически несовместны, т.е. их нельзя совместить без зазоров или наложений. Совокупность отсчетных форм слоев сборки играет ту же роль, что и натуральная форма тела в классической теории упругости: относительно этих форм вычисляются меры деформаций, входящие как аргументы в функцию запасенной упругой энергии. В наиболее простых постановках задач для самонапряженных слоистых структур отсчетные формы слоев полагаются заранее известными (в [32,33] им соответствует случай заданной отсчетной геометрии). Однако, если задача предполагает моделирование некоторого процесса послойного создания трехмерного тела, отсчетные формы его слоев заранее неизвестны и должны быть определены из некоторых дополнительных условий, характеризующих технологию процесса. В рамках настоящей работы будем полагать, что эти условия определяют геометрические соотношения для формы слоя в составе сборки на момент его присоединения и формы того же слоя в ненапряженном состоянии. В частности, такие соотношения характеризуют усадку, происходящую при фотохимической солидификации полимера, температурные деформации при охлаждении осажденного слоя и т.п. Следуя [34,38,39], будем называть краевую задачу с неизвестными отсчетными формами слоев, но дополненную условиями для их определения эволюционной задачей .
-
4 o . Для формализации эволюционной задачи рассмотрим семейство G = {Ba }ае1 гладких трехмерных тел, упорядоченных относительно вложения, т.е.
Va, pel:(a
Кроме того, будем полагать, что Ba -подмногообразие B, т.е. тело Ba как топологическое пространство, обладает топологией, индуцированной B . Образно говоря, это условие означает, что все тела из G топологически эквивалентны и могут быть получены непрерывным отображением некоторого «модельного» тела. Для задачи, исследуемой в настоящей работе, это тело - полый шар, скажем, с единичным внешним радиусом и радиусом полости, равным 1/2. Поскольку в этом разделе рассматриваются сборки, состоящие из конечного числа слоев, то множество индексов П имеет конечную мощность и без ограничения общности его можно считать конечным отрезком натурального ряда, т.е. I = { 0,1, ..., N } , N > 1. Элементы семейства G , т.е. тела B, будем называть промежуточными сборками, B - начальным телом, BN - финальным телом [40].
-
5 o . Каждая сборка, т.е. тело Ba e G , является результатом соединения конечного числа слоев. Несмотря на то что представление тела как соединение
его частей и, наоборот, разбиение его на конечные части часто используется в механике континуума, применение стандартных теоретико-множественных операций для определения таких разложений затрудняется следующим обстоятельством. Тела B, будучи гладкими подмногообразиями финального тела BN , являются открытыми подмножествами BN [37]. На первый взгляд, слой сборки может быть определен как теоретико-множественная разность двух смежных тел, B и B , однако она не является открытым множеством, и поэтому не является гладким телом. Кроме того, теоретико-множественное объединение тела - промежуточной сборки и тела - слоя не будет содержать их общую границу и, следовательно, не может представлять следующую по порядку сборку. Эти сложности могут быть преодолены за счет введения особой операции над множествами, представляющими тела, - операции соединения v :
B a V L . : = B a ^L .+ 1 ' ( B e+ i \ B a ) = B .. , , (1)
Здесь Lj= Int (Ba+3 Ba ) - тело-слой, дополняющее промежуточную сборку B до следующей по порядку сборки Ba+1, Int Z - внутренность множества Z в топологии BN, d^ Z - граница множества Z в топологии B (напомним, что B - подмножество BN и его топология индуцируется из BN ). Формула (1) имеет ясный геометрический смысл: тело-сборка B является объединением трех множеств: предшествующей сборки B , слоя L и общей части границы B и La+т. Таким образом, операция соединения v формализует процесс «склеивания» двух тел с общей границей, точки которой включаются в состав тела и изменяют свой статус с граничных на внутренние. Разложение промежуточного тела-сборки на составляющие его слои может быть записано в виде [39]
B + = B o v L 1 v_v L . L a+ 1 , L o : = B>- (2)
Физическое пространство, вмещающее формы тел-сборок и тел-слоев, полагаем трехмерным аффинноевклидовым, т.е. тройкой ( 8, У, • ) , где 8 - множество, элементами которого являются места материальных точек, V - трансляционное векторное пространство со скалярным произведением ( • ) .
Будем полагать, что формы тел-сборок и тел-слоев подчинены условиям:
-
А. Актуальные формы тел Ba e G, так же как и составляющих их слоев L, - полые шары в 8 , т.е. множества мест Ba и L^, соответственно:
B a = { х e£ | г . <|| х - o^r . },
L ae = { x ef 1 r . , e< II х - o il < r a e , в }-
Здесь индекс ос обозначает номер сборки, а индекс в - номер слоя.
-
В. Натуральные формы слоев – полые шары в , т.е.
L a = { x e£ | R <|| x - о ||< R a }.
-
С. Внутренний, R i , и внешний, R e , радиусы ненапряженной формы тела-слоя L связаны
с внешним радиусом актуальной формы тела-сборки B соотношениями
Ra+1 = Sa+1 ra , Ra+1 = Ra+1 + Aa+1, где Aa, a = 1,2, _ , N - заданные толщины слоев в ненапряженном состоянии; S – величины, определяющие зазоры (при Sa+t > 1) или наложения (при 5a+j < 1 ) ненапряженных слоев и характеризующие технологическую усадку при солидификации слоя2.
-
D. Заданы внутренний и внешний радиусы, Ri , Re , начального тела (т.е. слоя с номером 0).
Здесь и в дальнейшем используются следующие обозначения: одинарный нижний индекс обозначает номер соответствующего тела-слоя или тела-сборки, а двойной нижний индекс, элементы которого разделены запятой, – номер сборки и номер слоя в составе этой сборки.
С учетом принятых обозначений и формулы (2) последовательность форм тел-сборок может быть представлена диаграммой3 (рис. 1).
«Во ®1 ®2
£о------------------• £о v £1 . (£о V £|) V £2 • • •
| Ио I Xi j Х2
0,1.1»
Рис. 1. Последовательность форм тел-сборок
Fig. 1. The sequence of assemblies
Из предположений A–D следует, что для любого тела-сборки B существуют конфигурации , в = 0, _ , N , образы которых - полые шары в 8 , причем части этих шаров, соответствующие слоям с номером в , свободны от напряжений. Например, для тела-сборки с номером 2 существует три таких конфигурации; они показаны на диаграмме (рис. 2).
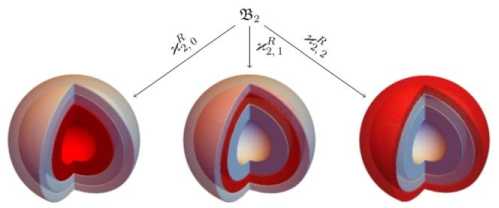
Рис. 2. Конфигурации для тела-сборки с номером 2 (выделение темным цветом соответствует форме, свободной от напряжений)
Fig. 2. Configurations for assembly with number 2 (stress free shapes are highlighted in dark)
-
1.2. Координаты и векторные базисы
-
6o. Поскольку, по предположению, физическое пространство евклидово, то в нем может быть определена декартова система координат ( o; ix , i2,i3 ) с началом в точке о е8 и ортонормированным базисом ( i M i 2 , i 3 ) : i s ^ , s e { 1,2,3 } ; i s • i p = 5 sp , где 5 sp -символ Кронекера. Так как формы всех сборок B и
- тел-слоев L обладают центральной симметрией, то, наряду с декартовыми координатами (x1, x2, x3) , в 8 удобно использовать сферические координаты (r, 0, ф), связанные с декартовыми формулами перехода:
x1 = r sin0 eosф, x2 = r sin0 sinф, x3 = reos0, r > 0,0 e J0, п[, ф e[0, 2n[, и отсчетные координаты (R ^, 0a p, Фа p) , связанные с координатами (r, 0, ф) соотношениями r = fa, в( Rx, в), 0 = ©a, в, ф = Фa, в. (3)
Здесь f р: R+ ^R+ - продолжение функции fa, в: [ R; ■ Кв ]^[ ra, в • r^ р J, являющееся гомеоморфизмом на свой образ. Функция4 f задает расстояние от начала координат o до актуальных позиций материальных точек формы L тела-слоя L в составе сборки B в зависимости от их отсчетных позиций в натуральной форме L . Каждая из таких координатных систем ассоциирована с формами слоев и играет роль «вмороженных» координат [41]. Таким образом, построен расширенный атлас физического пространства, содержащий, помимо декартовой карты, карты, определяемые различными вариантами сферических координат. Такое расширение позволяет упростить дальнейшие вычисления, используя различные координаты по мере необходимости.
Каждая координатная система порождает поле локальных базисов (векторных базисов, по терминологии | а,Р а,в а,р Л
[42]), т.е. троек векторов (er,eU,eф) и I eR,e0,e* I, касательных к соответствующим координатным линиям и определяемым формулами:
1.3. Меры деформаций
7o. Согласно (3) деформация каждого слоя L в составе сборки B из натуральной формы центральносимметрична (радиальные смещения задаются функцией f ). В связи с этим градиент деформации, транспонированный градиент деформации и тензоры Коши – Грина могут быть представлены диагональными диадными разложениями:
Fa, р = /а, вer ® eR + eu® e0 + eф® e*, а,Р а,р v а,р
т . а,в
Fa , в = / а, в e R ® e r +
( f А
V V в 7
,в e0 ®e6 +
Л
I R , в 7
а , в
■ e * ® e ф ,
В а , р = F a, в Fl , в = ( f , в ) 2 e r ® e r +
+
5x ec = - i, c e{r, 6, Ф};
dc а,в ars ( 2
e C = — i s , C a, ■ R a, в , ® а, в , Ф а, в } .
d C
I г "
V R , в
Ва. в =
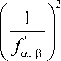
e H ® e 6 + и
2 f 1^] V R , в 7
e ф ® e ф ,
er ® e r +
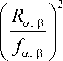
e6 ® e u +
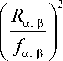
е ф ® е ф .
Дуальные к ним базисы (er,e6,eф) и eR,e0,eф v , , / \ а,в а,в а,в/ определяются соотношениями биортогональности:
а,в es - ec = 5s■, s, c e{r, U, ф}; e^-ec = 5c, s, c e{Rа, в , 0a, в , Фа, в}.
Здесь 5 s - символы Кронекера, принимающие значение 1 при совпадении s и c и 0 – в противном случае. Разложения используемых далее векторов локальных базисов по элементам декартова базиса приведены в табл. 1.
Таблица 1
Представление локальных базисов
Table 1
Representation of local bases
|
i 1 |
i 2 |
i 3 |
|
|
e r = e r = e R = e R а , p |
sin U cos 9 |
sin U sin ф |
cos U |
|
e и |
г cos U cos 9 |
r cos U sin ф |
- r sin U |
|
e ф |
- r s in U sin ф |
r s in U cos ф |
0 |
|
а , p e Θ |
R pCos U cos ф |
R pCos U sin ф |
- R , p sin U |
|
а , p e Φ |
- R pSin U sim p |
R pSin U cos ф |
0 |
|
e6 |
r -1cos U cos ф |
r -1cos U sin ф |
- r sin U |
|
e ф |
- ( г sin U ) - 1sin ф |
( г sin U ) " 1cos ф |
0 |
|
e Θ а ,p |
R " 1p Cos U cos ф |
R- 1p Cos U sin< p |
- R - 1 p sin U |
|
e Φ а ,P |
- ( R , в sin U ) - 1sin ф |
( R , p sin U ) " 1 cos ф |
0 |
Главные инварианты тензоров B определяются
соотношениями:
I f „^
1 1 ( В а, в ) = t Г В а , в = ( / , в ) + 2 I ,
V R a, в 7
1 2 ( В а, в ) = 1 ( ' Г ( В а, в ) " 1 1 ( B ! в ) ) =
= 2( / „, р ) 2
I V fA I
V R , P 7
1 fA V R , р
1 3 ( В а, p ) = det B a, p
= ( / -, P ) 2
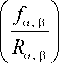
-
1.4. Несжимаемый материал
8o. Полагаем, что материал тел-слоев несжимаем, однороден и изотропен5, а плотность упругой энергии, запасаемой им при деформировании в составе тела-сборки, определяется двухконстантным потенциалом Муни – Ривлина:
W a ,p = C 1 ( 1 1 ( В а, p ) " 3 ) + C 2 ( 1 2 ( В а ,p ) - 3 ) . (6)
Константы (упругие модули) C , C могут быть выражены через другую пару модулей b и μ следующим образом: С = (1 +b)ц/4, C2 = (1—b)ц/4. Использование модулей C и С2 позволяет выражения, получае -мые далее, записать в более лаконичной форме, в то время как модули ц и b указывают на взаимосвязь нелинейной гиперупругой модели материала и линейно -упругой модели: при малых деформациях из ненапряженного состояния ц совпадает с модулем сдвига линейно-упругого несжимаемого материала.
Для потенциала (6) формула Ривлина [42, 44] определяет напряжения Коши:
T a , в = — p^ в I + 2 С В» в — 2 C 2 В — 1 в , (7)
где I- единичный тензор; pa ^ - гидростатическая компонента, определяемая из уравнения равновесия V • T = 0 и заданных краевых условий. Краевая задача для центрально-симметрично деформированного тела-сборки имеет вид а,в
' 2^а , в а , в^
V r е] rt , в , <, в [ ".-T- + - I t r • — T *l = 0, (8)
-r r ^ J а,в гр 0"
Т 0
a a , в( 2 r 3 — a a, в ) ■ ' r 4( r 3 — a a , в )4/3
X
а,в а,в
х ( С . ( r 3 — a a,в )2/3 + С - r 2 ) , 7 ^ = T t .
а ,в
10 o . Постоянные p 0, aa р должны быть выбраны так, чтобы удовлетворялись краевые условия (9) и (10). Подстановка выражений (11) и (12) в них приводит к системам нелинейных алгебраических уравнений. Для начального тела ( а = 0) система состоит из двух 0,0 уравнений относительно двух неизвестных, p 0, a 0 0:
0,0 г . 0,0
-
p 0 + ^|_ R 0 ; a 0,0 _| = q0 , p 0 + ^|_ R 0 ; a 0,0 _| = q 0 , (13)
где Т[ R ; a ] = ( R ( R 3 + а )4/3 )— 1 { С ( 5 R 3 + 4 a ) R 2 — 2 C х x ( R 3 + a )2/3 ( R 3 + 2 a ) } . Системы для остальных тел-сборок B , 0 < a < N (с учетом равенств R e = R + Лр , 0 < в < a) состоят из 2 a + 2 уравнений относительно 3 а+ 2 неизвестных р0, р0, ^ , 1^ 0 , a a , 0, a a ,j , ^ , a a , а , R i , R 2 , -, R a :
T a, p - e rL = T a, в+1 • e r[
' 'a , в '
= r a , в+ 1
r в = ' , в+1 - (10)
a,0 a,a p 0 + ^ |_ R0; aa, 0 ]= qa , p 0 +2'|_ Ra; aa, a ] = qa ,
Краевые условия (9) характеризуют равномерное гидростатическое нагружение сферических границ сборок, а (10) - условия идеального контакта между слоями.
9 o . Решения уравнения (8) могут быть определены следующим образом. Поскольку входящие в него функции являются функциями радиальной координаты, то оно является обыкновенным дифференциальным уравнением. Интегрируя его, имеем [42, 44]
( R e )3 + a a, 0 = ( R i )3 + a a ,1 , (14)
a, a—1
p 0 +t R a —1 ;
a
a ,a
p 0 +^ R a ;
a a, a
,
( R a—1 )3 + a a, a—1 = ( R a )3 + a a, a -
а , в а,в 9 Г а , в а , в^
T ' = Р 0 + 1 4 T — T r ' ldr, r I J
а ,в где p 0 - постоянная интегрирования. С учетом соотно-a ,в а ,в шения (7) и формул (4), (5) для разности T^ — Tr' интегрирование дает
^в-,"^ С, ( 5 r 3 — a a , в ) ( r 3 — a a , в ) 3 — 2 С 2 ' 2 ( r 3 + a a , в )
• r p 0 r 4( r 3 — a a , в )1/3 Л ’ где а а р - параметр деформации6. Полученная формула (11) позволяет определить функцию p . Тогда, используя (7), получаем
6 Поскольку материал несжимаемый ( det F р = 1 ) , то f a , в =( Ra, в + a a , в ) -
Условие С дает N — 1 уравнение, дополняющее систему (14):
R a = S a V( R a—1 )3 + a a—1, a—1 ,0 N , (15)
которое преобразует недоопределенные по отдельности уравнения (14) в рекуррентную последовательность систем уравнений. Система (13) является базой 0,0
рекурсии. Решая эту систему, определяем p 0 и a0 0 . По известному значению a из (15) определяем Ri . Первый шаг рекурсии - система (14) для а = 1- система четырех уравнений относительно четырех 1,01,1
неизвестных p 0, p 0, a 0, a г По известному a i из (15) определяем R i . Второй шаг рекурсии - система (14) для а = 2 - система шести уравнений
2,0 2,12,2
относительно p 0, p 0, p 0, a 2 0, a2 р a 2 2. Решая после-
довательно системы нелинейных уравнений, определяем все постоянные интегрирования в (11) и (12).
1.5. Сжимаемый материал
fL fa ,
Г .
( f ,p )2
R 2, в
2 ,
в
= о.
11 o . Для сжимаемого материала плотность упругой энергии слоя L^ задается трехконстантным потенциалом Муни - Ривлина
W , = C , ( J S I . - 3 C . ( JI , - - 2( J .,—»- .
Краевые условия представлены выражениями (9), (10). Таким образом, для фиксированного а краевая задача относительно функций f р имеет вид
V R е] R p , R [ : Ф ( f a, в , f ,p ) + ^ = 0,
в котором Jа , р = det F a, р = f a, р ( f ,, р / R a, р ) 2 * 1 , постоянная d соответствует модулю объемного расширения. В этом случае выражение для тензора напряжений Коши Та р примет вид [44]
V ( f a, о , fa„ 0 ) I R = R = q ‘a , V ( f a, a , f^ | r = R = q . , VPе { 0,l, _ , a — 1 } : f . p R = r. = f . „, R = R p
V ( f a, в , f a , p ) R = R . = V ( f a, p+ 1 , f a.+1 ) R = R P „ ,
Ф ( f , f ‘ ) = ( Rf { f 8 ( 9 / 4 d f '2 J 4,3 — 7 C 2 ) + C 1 R 8 J 8/3 +
2 5W„ „
T 0=--- Вв --— = Ро I + в B 'Р 1 B Л, (16)
a, р т a, р дп "0 "1 a, р “—1 a, р’ х /
J a, в ^^a, в
+ R 2 f 6 ( 5 C 1 J2/3 + C 2 f '2 ) } ) — 1 X
где B a , в = F a , в F T в , а в0 , Р 1 , в—1 - скалярные функции
X { f ' ( f — Rf ') (2 f 8 C 2
—
9 . 4 ^
9 df ,2 J 3 +
реакции,
3 d ( I R2 в о =
—
1 ) I 7 — 2 CIJ 1 /3 + 2 C2I2
3^ ’
+ CR 8 J 3 — 9 cyR 3 f5 f' J 2/3 —
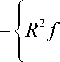
Г 2
4 C 1 J 3
— C 2 f '2 1 + 9 C 2 Rf 7 f * ^ )},
Р.= 2C1 Р =-^ в1 г5/6 , в—1Я/6
I 3
Элементарные вычисления приводят к следующим выражениям для напряжений Коши (16):
a,в a,вa
Ta, ₽= Trrer ® er + T eв® e^T^'eф® eф, a,p 4.
T Г = 3 R —4 в J —7 в 3 { f a 4 , в ( 3/4 d J ^ ( J a , в — 1 ) ( f a, p ) 2 — C 2 ) +
+C R8, в J^ С — R2, в £ в (CJ£ — Cf в )2)}, a,в a,в
T* O' _ ТФ' _ 2 П —4 r—7/3
T O = Т ф = g R a, в J a, в X
X { f 4, в ( 3/2 d J^ ( J a, в — 1 ) ( 4 в ) 2 + C 2 ) —
— CR в С f —в + R 2, в f , в ( CJ- — C - f в )2 ) }.
Для центральной симметрии уравнение равновесия
V- T = 0 сводится к одному скалярному уравнению d TГ ■
5 R a , в
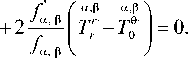
Подставляя выражение (17) в последнее уравнение, приходим к обыкновенному дифференциальному уравнению второго порядка относительно неизвестной функции f a , в :
в о +в 1 ( 4р )2 +в —1
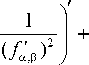
V ( f , f ') = 2(3 f 8 f '4 Г1 J 5,3 x
X ( R 4 f 4 ( — 3 C2f '6 — C 2 + 3/2 d J 1/3 ( J — 1 ) f '2 ) +
+ R 8 f '2 ( 2 C 1 J2/3 + 3 C 2 f '2 ) — '
— 2 R 6 f 2 ( C 1 J2/3 + C 2 f '2 ) + 3 C 2 f 8 f '2 ? *
В качестве начального приближения для решения краевой задачи, соответствующей сжимаемому материалу, используется решение для несжимаемого материала. В свою очередь, это решение получено с использованием решения линейной задачи как начального приближения. Рис. 3, 4 иллюстрируют различия напряженных состояний, полученных для одного полого шара с использованием различных уравнений состояния для линейно-упругого, гиперупругого несжимаемого и гиперупругого сжимаемого материалов. Постоянная гидростатическая нагрузка полагалась равной 0,2р. и 0,7 р . На графиках, приведенных на рис. 3, показаны распределения радиальных и окружных компонент напряжений Коши, соответствующие линейной и нелинейной моделям сжимаемого материала (здесь и далее R - внутренний радиус начального тела). При этом компоненты тензора напряжений, соответствующие линейной модели, имеют вид [45, 46]
D3 ( п3 А п 3 ( п 3 А
( rr ) _ R 2 R L-1 Т<") R 2 I 1 I R 1
T q 1 1 1 1 , T q 1 1 1 + 1 .
R 13 — R 23 ( R 3 J 4R— — R 23 ( 2 R 3 J
Здесь q - гидростатическая нагрузка, Rx < R - отсчетные радиусы полого шара.
На графиках, приведенных на рис. 4, показаны распределения разностей напряжений, соответствующих сжимаемой и несжимаемой нелинейным моделям. Приведенные графики иллюстрируют, что напряженное состояние в сжимаемой модели может существенно отличаться от соответствующих состояний в линейной и нелинейной моделях. Это показывает, что влияние нелинейности отклика и сжимаемости материала может оказаться весьма существенным.
Результаты вычислительного моделирования системы полых шаров, ненапряженные формы которых определяются из рекуррентных соотношений (18) при заданной послойной усадке S, иллюстрируются графиками на рис. 5, 6. Рассматривались системы, состоящие из 15 сферических слоев. Параметры гиперупругого материала брались теми же, что и в предыдущем расчете. Усадка S варьировалась в диапазоне [— 0,4; 1,6] (отрицательное значение S соответствует объемному расширению). Распределения радиальных и окружных компонент напряжений Коши, возникающих в самонапряженной структуре в отсутствие внешних силовых полей, показаны на рис. 5. В ходе решения рекуррентной последовательности краевых задач (18) при заданном значении S определяются внешние и внутренние радиусы ненапряженных шаровых форм. Эти формы геометрически несовместны: при их соединении возникают зазоры или наложения. Иллюстрация этого факта при различных значениях S приведена на рис. 6. На нем показаны экваториальные сечения ненапряженных шаровых слоев, которые расположены вплотную друг к другу вдоль радиуса, указанного жирной линией. Вдоль других направлений сечения располагаются с наложениями или зазорами.
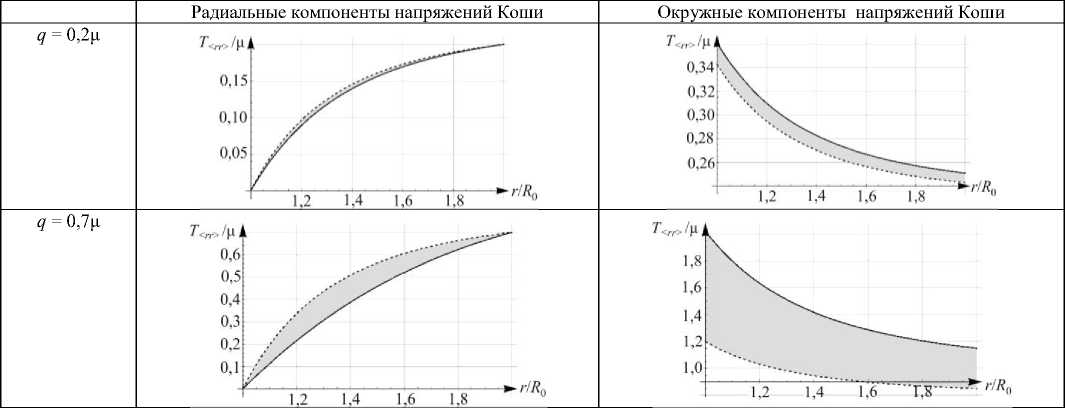
Рис. 3. Сравнительные графики напряжений, полученных из линейно-упругой (пунктирная линия) и гиперупругой моделей (сплошная линия)
Fig. 3. Comparative graphs of stresses for linear-elastic (dotted line) and hyperelastic models (solid line)
|
Радиальные компоненты напряжений Коши |
Окружные компоненты напряжений Коши |
|
|
q = 0,2μ |
хт /т t-*1 0,005 .....12 ' il^TF "riR» -0,005 -0,010 -0,015 Г -0,020 -0,025 |
АТ^/Т^а» --------- 0,002 1,2 1,4 1,6 1,8 " -0,002 / -0,004' |
|
q = 0,7μ |
AZ^»/^ 0,1 1,2 1,4 1.6.—-*#-" ',R" -0,1 |
A7^gg>/T<g0> 0,1 S'" 0,10 ■ 0,05 1.2 1.4 1.6 " |
Рис. 4. Сравнительные графики напряжений, полученные из гиперупругих моделей для несжимаемого и сжимаемого материалов
Fig. 4. Comparative graphs of stresses obtained for hyperelastic models of incompressible and compressible materials
Радиальные компоненты напряжений Коши
Окружные компоненты напряжений Коши
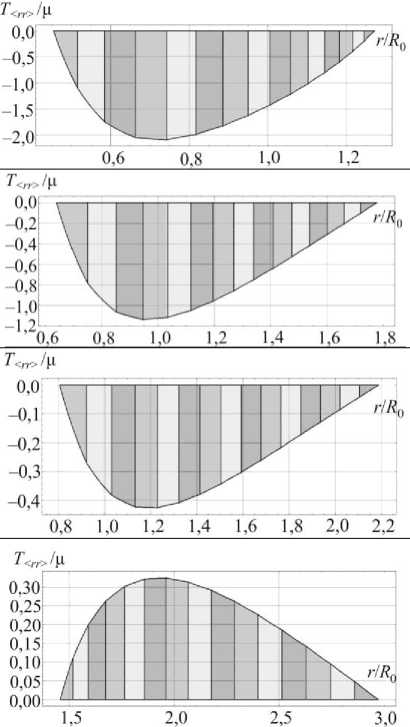
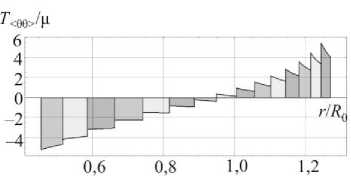
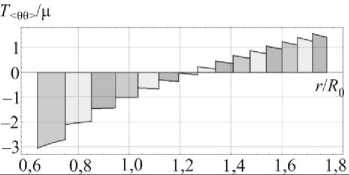
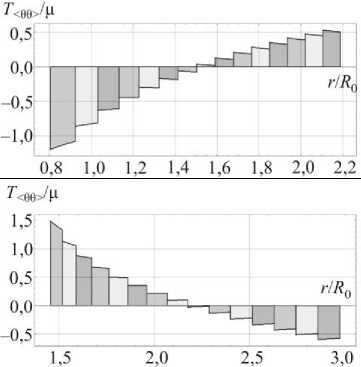
Рис. 5. Распределения напряжений в самонапряженной структуре в отсутствие внешних силовых полей
-
Fig. 5. The distribution of stresses in self-stressed structure with an absence of external force fields
S = –0,4
S = 0,1
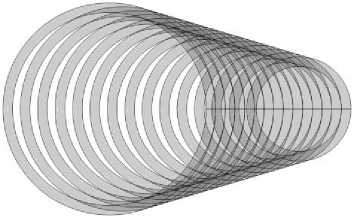
S = 0,6


S = 1,6

Рис. 6. Наложения ненапряженных отсчетных форм (изображены экваториальные сечения ненапряженных шаровых слоев)
-
Fig. 6. Overlaps of the stress-free reference shapes (equatorial sections of non-stressed spherical layers are shown)
2. Непрерывные неевклидовы структуры
12o. Для определения напряженно-деформированного состояния слоистых структур приходится решать системы нелинейных уравнений (18), что для большого числа слоев становится вычислительно сложной задачей. В то же время «измельчение» слоев, т.е. увеличение их числа и уменьшение толщины при фиксированной суммарной толщине и достаточно медленном изменении параметров процесса послойной сборки, S , qi , qe , приводит к распределениям для напряжений и деформаций, близким к непрерывным. В связи с этим представляется целесообразным для анализа слоистых структур с большим количеством слоев предварительно осуществлять их континуализацию, позволяющую заменить разрывные распределения для компонент меры деформаций Коши – Грина непрерывными аппроксимациями, близкими к исходным в некотором, определенном заранее, смысле. В рамках настоящей работы в качестве таких аппроксимаций используются полиномы, коэффициенты которых определяются из условий наименьших квадратичных отклонений от разрывных распределений.
Аппроксимируются диагональные компоненты тензорного поля
F n : [ r i , r e p Lin ( V; V) , характеризующего послойно несовместные деформации финального тела:
F n = A n e r 0 e r + a N e . 0 e 6 + a N e ^ 0 e 9 , (19)
a N ( r ) = ‘
где A и a – кусочно-непрерывные функции актуаль-
ной формы:
A N ( r ) = <
{ fN\M r ) ’
T / iN W) ’
r -[ r N , o , r N , о ] ; r e[ r N ,1 , r N ,1 ] ;
. { f N' 4( r ) ’ r ’ rN , N ’ N N ] ,
r
f N >) ’
r
f ^H ’
r
I ^, N ( r ) ’
r -[ r i ,0 ,
;
;
Функцию (19) можно рассматривать как «склейку» полей градиентов деформации каждого слоя из ненапряженного состояния, записанных в переменных актуальной формы. Поскольку в этих переменных области определения «склеиваемых» полей – смежные подобласти актуальной формы B , то результатом будет непрерывное тензорное поле, определенное на отрезке [ r N , r N ] .
Обозначим через А и а аппроксимации функций A и a , заданных формулой (20). Им соответствует тензор F – аппроксимация F :
F = Aer 0 e r + a e 6 0 e 6 + a e^ 0 e 9 . (21)
Для сравнения рассматриваются тела-сборки, состоящие из 5, 10, 20, 100 и 200 слоев, суммарная
толщина которых в ненапряженном состоянии равна 0,3 R . Упругие модули принимались равными Х = 2 ц , d = 4 ц , b = ц /2, ненапряженные формы слоев совпадают с ненапряженной формой подложки, qa = q e = 0. Аппроксимирующие многочлены приведены в табл. 2.
Сопоставление графиков разрывных функций и аппроксимаций для 5, 10, 30 слоев показано на рис. 7. Для большего числа слоев графики этих функций типографически неразличимы.
13o. В результате перехода к непрерывным функциям ra , rA финальное тело-сборка B становится неевклидовым телом B в том смысле, что его натуральная (свободная от напряжений) форма может быть определена только в пространстве с неевклидовой связностью.
Таблица 2
Аппроксимирующие многочлены
Table 2
Approximating polynomials
α
A
a
5
- 15,093 r 4 + 74,889 r 3 -134,463 r 2 + 103,332 r - 27,638
- 1,768 r 4 -4,024 r 3 + 24,203 r 2 - 28,263 r + 10,816
10
- 9,617 r 4 + 42,167 r 3 -67,697 r 2 + 46,103 r - 9,954
4,450 r 4 - 21,559 r 3 + 38,210 r 2 - 28,536 r + 8,418
30
- 1,267 r 4 + 4,524 r 3 -4,654 r 2 - 0,411 r + 2,796
0,951 r 4 - 4,265 r 3 + 7,101 r 2 -4,211 r + 1,419
50
- 0,241 r 4 + 0,058 r 3 + 2,594 r 2 - 5,605 r + 4,180
0,378 r 4 - 1,680 r 3 + 2,774 r 2 - 1,022 r + 0,547
100
0,236 r 4 - 2,008 r 3 + 5,927 r 2 -7,979 r + 4,808
0,101 r 4 - 0,447 r 3 + 0,735 r 2 + 0,466 r + 0,143
200
0,364 r 4 - 2,561 r 3 + 6,816 r 2 - 8,610 r + 4,973
0,026 r 4 -0,115 r 3 + 0,189 r 2 + 0,863 r + 0,037
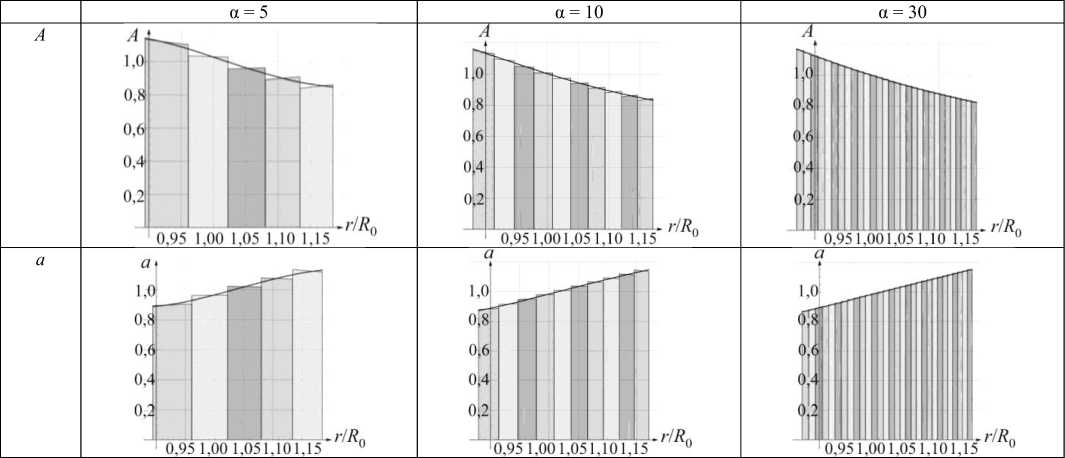
Рис. 7. Сопоставление дискретных и непрерывных распределений
-
Fig. 7. Comparison of discrete and continuous distributions
Согласно терминологии [21] такая связность называется материальной и может быть определена различными способами. Один из них – синтез материальной метрики [21, 35, 36] – состоит в том, что каждой материальной точке X финального тела сопоставляется метрика (соответствующего касательного пространства), определяемая как
^u,v e TxBn :GX (u,v) = KX [u]- KX [v)], где K – тензорное поле, определенное на B , называемое полем локальных конфигураций [21].
Поле K «склеено» из градиентов конфигураций xR : BN ^ 8, принадлежащих континуальному семей -ству {хR }ж<_^ , т.е. K = T^xR ; здесь Т - операция взятия дифференциала [37]. Каждый элемент семейства, R , переводит инфинитезимальную окрестность точки X в ненапряженное состояние. Соотношение между локальной конфигурацией K в точке X e BN и отображением R иллюстрируется диаграммой
~ Кх1 TXBN----^
Актуальная форма тела B , полученного в результате континуализации, совпадает с актуальной формой тела BN, т.е. с BN. Пусть j<: BN ^8 - актуальная конфигурация. Соотношения между телом B , его актуальной формой B и одной из его отсчетных форм
B R = xR ( BN ) иллюстрирует диаграмма
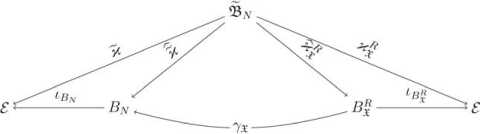
На диаграмме: ic: C ^8 - отображение вложения, действующее по правилу ic ( p ) = p . Отображение ух = х о [ ^ R ] -1 ух = х о [ ^ R ] -1 -деформация, переводящая свободную от напряжений окрестность точки X = r R ( X ) в ее актуальную форму.
Замечание 1 . В результате континуализации свободные от напряжений формы слоев, составляющих финальное тело B , вырождаются в сферы. Таким образом, форма BR обладает следующим свойством: не только точка X = xRX ( X ) , но и точки, лежащие вместе с ней на некоторой сфере, свободны от напряжений. Ф
-
14o. Для получения координатного представления полей, заданных на теле B , выберем в нем систему локальных координат. Используя картрирование актуальной формы B сферическими координатами ( r, 6, ф ) и актуальную конфигурацию х , определим координатное отображение
С = Co Л: BN ^ R3
на теле BN. Здесь C: x i—»(r, 6, ф) - координатное отображение, соответствующее сферическим коорди- натам. Обозначим координатный репер на теле B , соответствующий (r, 0, ф) , через (бг, д0, 5ф). Это векторное поле на B ; в каждой точке X тела B упорядоченная тройка (дг |х, 50 |х, 5ф |х) является базисом касательного пространства T B . Через (dr, d0, dф) обозначим корепер на BN, связанный с координатным репером равенствами de(dк ) = 5ck,c,k е {r,0,ф}.
В паре выбранных систем координат на B и актуальная конфигурация и ее градиент имеют представления в виде тождественных отображений хс = CoС\С\- = Id, Ти = er 0dr+e0 0d0 + e^ 0dф.
G = A 2 dr 0 dr + r 2 a 2 d 00 d 0 + r 2 sin 2 0 a - 2 d ф0 d ф. (22)
Построенная таким образом метрика на всем теле B превращает его в риманово пространство, связность которого определяется по формуле Леви-Чивита:
kl rj = T(dGi +5jGa -dGj), где Gj = gsK'Kj.
Для рассматриваемой задачи отличные от нуля коэффициенты связности определяются следующим образом:
г i- _ A '( r ) ri" - rA ( r )2 ( ra '( r ) - a ( r ))
-
r33 = a(r)3 ’
-
2 • • 2 • • 3 • • 3 • • _ 1 a ( r )
Г233 = - sin 0 cos 0 , Г323 = Г332 = ctg 0 .
Отличие этой связности от евклидовой характеризуется скалярной кривизной (инвариантом Риччи):
Ric (r) = 2(-5r2 A( r )2 a ‘(r )2 + 2 ra (r) A (r) x x ( rA ( r ) a"( r ) + a ‘(r )(rA ( r ) + 3 A (r )))-
-
- a(r )2 A ( r ) ( 2 rA '( r ) + A ( r ) ) + a ( r ) 4 ) / ( r 2 a ( r )2 ) . (24)
На рис. 8 показано распределение скалярной кривизны (24) для аппроксимационного многочлена, построенного на основе дискретного распределения при a = 200.
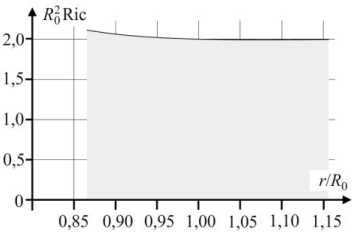
Рис. 8. Скалярная кривизна для случая α = 200
Fig. 8. Scalar curvature for the case α = 200
-
16o. Тензор напряжений Коши T , соответствующий непрерывному телу B , задан на актуальной форме B и является аппроксимацией тензора напряжений Коши Т , компоненты которого вычисляются по формулам (17). Таким образом,
T = T r er 0 e r + T 0 ee 0 e 0 + T ^ e^ 0 е ф , (25)
T = 4 J "7/3 \( a ( r )4 (3 d ( J - 1 ) J 1/3 A ( r )2 - C 2 ) +
+ CJ8/3a ( r ) - 4 - a ( r )2 ( CJ3,3 - C^A ( r )2 ) ] ,
T 0 = Т фф = 2 J -™\ a ( r ) 4 (3 d ( J - 1 ) J 3 A ( r ) 2 + C 2 ) - 8
-
- CJ 3 a ( r ) -4 + a ( r ) 2
CJ 3 - CA ( r ) 2 )
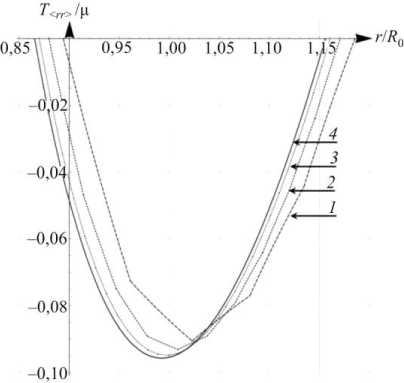
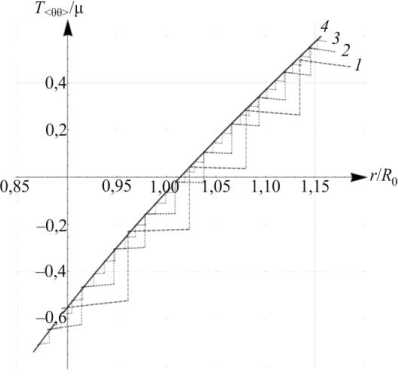
где J = det F = A ( r ) a ( r ) 2 . На рис. 9 приведены распределения физических компонент тензора напряжений T на отрезке ^ r i , r e J радиальных координат актуальной формы. Эти распределения сопоставляются с соответствующими распределениями компонент тензора напряжений T (17) в дискретных структурах при разных значениях N . Рис. 9 иллюстрирует, что с увеличением N распределения T стремятся к T .
-
17o. Определение отсчетной ненапряженной формы финального тела B с заданной на нем связностью (пусть даже неевклидовой) позволяет определить напряжения Пиолы [16, 19].
Для того чтобы получить представления в «отсчетных» координатах для неевклидова тела B , предполагается использовать формализм геометрической механики континуума [16, 19, 22]. При этом материальное тело и физическое пространство рассматриваются как однотипные объекты – гладкие многообразия с определенной на них аффинной связностью. Связность физического многообразия евклидова, а связность на многообразии B (материальная связность) – неевклидова и определяется коэффициентами связности (23).
a б
Рис. 9. Радиальные ( a ) и окружные ( б ) физические компоненты T ( 1 – 5 слоев, 2 – 10 слоев, 3 – 30 слоев, 4 (непрерывная линия) – непрерывная неевклидова структура)
Fig. 9. Radial ( a ) and circumferential ( b ) physical components of T ( 1 is 5 layers, 2 is 10 layers, 3 is 30 layers, 4 (solid line) is non-Euclidean solid)
Напряжения Коши Т интерпретируются как ковек-торнозначные 2-формы [19], а напряжения Пиолы Р – как pullback этих форм относительно конфигурации :
P = * T T .
Замечание 2 . Уравнения баланса импульса в переменных карт на многообразии B имеют вид [19]
Г д i
Здесь J = det I — I, g = det (gy) и G = det (G9 ). Функ- ции T – ковариантные компоненты тензора напряжений Коши (25). Тензор g представляет метрику на , а тензор G – материальную метрику на B . Тензор [Tйут - транспонированный к обратному тензору ТX , определяемый из равенства
D P + B ®р о ц о = V b ®р о И о.
V u eV V v е ТB N : G ( Tx 1 ( u ) , v ) = g ( u , [ t xT T ( v ) ) .
Здесь D – оператор Картана, являющийся обобщением операции дивергенции; В – ковекторное поле, соответствующее плотности массовых сил; V – скорость движения частиц тела в материальном описании; μ – форма объема, порождаемая метрикой тела G; (•)b - музыкальный изоморфизм [37], соответствующий метрике G, переводящий ковекторные поля в векторные поля. Важно отметить, что уравнения баланса определены на всем теле B , а не послойно, что позволяет осуществлять эффективные вычисления для большого числа слоев. 4
-
18o. Формула (26) позволяет по заданному тензору напряжений Коши определить тензор напряжений Пиолы. Именно, пусть ( X ) - локальные координаты на теле BN , а ( Xa ) - криволинейные координаты в в .
Тогда компоненты тензора напряжений Пиолы, p = P^dX 0 d X е , определяются формулой [39]
P a , = J T ab ([ T^ T ) Ь .
Для вычисления компонент тензора напряжений Пиолы выберем в физическом пространстве сферические координаты (r, 0, ф), а на теле BN - координаты (r, 0, ф) согласно п. 140. Тогда
Tr = т, те9= rгт00, Тфф= r2sin20 тф, где T i определены формулами (25). Метрика g имеет представление
g = er 0 er + r2ee 0 ee + r2sin2еeф 0 еф, а G представлена формулой (22). В этой связи g / G = a2A , где учтено, что A > 0 . Поскольку матрица компонент Тх единичная, то J = 1 и мы приходим к окончательным выражениям для компонент тензора P:
P rr = -T rr , P ee = A r2T ^ , Р фф = A r 2sin2 e Т ф .
19o. При большом числе слоев самонапряженной слоистой структуры кусочно-непрерывные параметры деформации могут быть аппроксимированы непрерывными функциями. При такой аппроксимации отсчетная форма может быть определена в пространстве с аффинной (неевклидовой) связностью. Получаемая при этом математическая модель самонапряженного тела эквивалентна нелинейной модели тела с распределенными дефектами. В рамках этой модели методами геометрической механики континуума могут быть определены обобщенные представления для напряжений Коши и Пиолы. Вычисления, проводимые для дискретной структуры и тела с неевклидовой отсчетной формой, определяемой аппроксимацией параметров деформации, численно
иллюстрируют сходимость решений дискретной модели к непрерывной при увеличении числа слоев с неизменной суммарной их толщиной.
Работа выполнена при поддержке РФФИ 18-08-01346, РФФИ 19-58-52004 МНТ_а, РФФИ 18-01-00812 и по темам государственного задания (номер госрегистрации АААА-А17-117021310373-3 и АААА-А17-117021310379-5).
The work was performed with partial financial support from the RFBR No. 18-08-01346, RFBR No. 19-58-52004. RFBR No. 18-01-00812 and FASO (Projects No. AAAA-A17-117021310373-3 and АААА-А17-117021310379-5).
Список литературы Нелинейная эволюционная задача для самонапряженных слоистых гиперупругих сферических тел
- Prokop A., Davidson J.M. Nanovehicular intracellular delivery systems // Journal of Pharmaceutical Sciences. – 2008. – Vol. 97, no. 9. – Р. 3518–3590. DOI: 10.1002/jps.21270
- Caruso F. Nanoengineering of particle surfaces // Advanced Materials. – 2001. – Vol. 13, no. 1. – P. 11–22. DOI: 10.1002/1521-4095(200101)13:1-11::AID-ADMA11-3.0.CO;2-N
- Schärtl W. Crosslinked spherical nanoparticles with core–shell topology // Advanced Materials. – 2000. – Vol. 12, no. 24. – P. 1899–1908. DOI: 10.1002/1521-4095(200012)12:24-1899::AID-ADMA1899-3.0.CO;2-T
- Wang X.M., Xiao P. Non-template synthesis of titania hollow spheres and their thermal stability // Journal of Materials Research. – 2005. – Vol. 20, no. 4. – P. 796–800. DOI: 10.1557/JMR.2005.0130
- Caruso R.A., Susha A., Caruso F. Multilayered titania, silica, and laponite nanoparticle coatings on polystyrene colloidal templates and resulting inorganic hollow spheres // Chemistry of Materials. – 2001. – Vol. 13, no. 2. – P. 400–409. DOI: 10.1021/cm001175a
- Liang Z., Susha A., Caruso F. Gold nanoparticle-based core-shell and hollow spheres and ordered assemblies thereof // Chemistry of Materials. – 2003. – Vol. 15, no. 16. – P. 3176–3183. DOI: 10.1021/cm031014h
- Growth of semiconducting GaN hollow spheres and nanotubes with very thin shells via a controllable liquid gallium-gas interface chemical reaction / L.-W. Yin, Y. Bando, M.-S. Li, D. Golberg // Small. – 2005. – Vol. 1, no. 11. – P. 1094–1099. DOI: 10.1002/smll.200500168
- Martin P.M. Handbook of Deposition Technologies for Films and Coatings: Science, Applications and Technology. – William Andrew Pub., 2009. – 936 p.
- Molecular Beam Epitaxy: An Overview / P. Frigeri, L. Seravalli, G. Trevisi, S. Franchi // In book: Comprehensive Semiconductor Science and Technology / Editors: Pallab Bhattacharya, Roberto Fornari, Hiroshi Kimamura. – Elsevier, 2011. P. 480–522
- Multilayer Thin Films / Ed. by Gero Decher, Joe B. Schlenoff. – Wiley VCH Verlag GmbH, 2012. – 1100 p. DOI: 10.1002/9783527646746
- Innovation in layer-by-layer assembly / J.J. Richardson, J. Cui, M. Björnmalm [et al.] // Chemical Reviews. – 2016. – Vol. 116, no. 23. – P. 14828–14867. DOI: 10.1021/acs.chemrev.6b00627
- Mechanical Self-Assembly / ed. by Xi Chen. – New York: Springer, 2012. – 206 p. DOI: 10.1007/978-1-4614-4562-3
- Yu B., Pan D.Z. Design for Manufacturability with Advanced Lithography. – Springer International Publishing, 2015. – 164 p. DOI: 10.1007/978-3-319-20385-0
- Strained silicon as a new electro-optic material / R.S. Jacobsen, K.N. Andersen, P.I. Borel [et al.] // Nature. – 2006. – Vol. 441. – P. 441:199–202. DOI: 10.1038/nature04706
- Maugin G.A. Material inhomogeneities in elasticity. – CRC Press, 1993. – 292 p.
- Marsden J.E., Hughes T.J. Mathematical foundations of elasticity. – Courier Corporation, 1994. – 576 p.
- Segev R., Rodnay G. Cauchy's Theorem on Manifolds // Journal of Elasticity. - 1999. - Vol. 56, iss. 2. – P. 129–144. DOI: 10.1023/A:1007651917362
- Epstein M., Elzanowski M. Material inhomogeneities and their evolution: A geometric approach. – Springer Science & Business Media, 2007. – 274 p.
- On the geometric character of stress in continuum mechanics / E. Kanso, M. Arroyo, Y. Tong [et al.] // Zeitschrift für angewandte Mathematik und Physik. – 2007. – Vol. 58, iss. 5. – P. 843–856. DOI: 10.1007/s00033-007-6141-8
- Лычев С.А., Манжиров А.В. Математическая теория растущих тел. Конечные деформации // ПММ. – 2013. – Т. 77. – С. 585–604.
- Noll W. Materially uniform simple bodies with inhomoge-neities // Archive for Rational Mechanics and Analysis. – 1967. – Vol. 27, no. 1. – P. 1–32.
- Yavari A., Goriely A. Riemann–Cartan geometry of nonlinear disclination mechanics // Mathematics and Mechanics of Solids. – 2012. – Vol. 18, no. 1. – P. 91–102. DOI: 10.1177/1081286511436137
- Epstein M. The Geometrical Language of Continuum Mechanics. Cambridge University Press, 2010. – 326 p.
- Lazar M. On the fundamentals of the three-dimensional translation gauge theory of dislocations // Mathematics and Mechanics of Solids. - 2010. - Vol. 16, iss. 3. – P. 253-264. DOI: 10.1177/1081286510370889
- Yavari A., Marsden J.E., Ortiz M. On spatial and material covariant balance laws in elasticity // Journal of Mathematical Physics. – 2006. – Vol. 47, no. 4. – P. 042903. DOI: 10.1063/1.2190827
- Yavari A., Ozakin A. Covariance in linearized elasticity // Zeitschrift für angewandte Mathematik und Physik. – 2008. – Vol. 59, no. 6. – P. 1081–1110. DOI: 10.1007/s00033-007-7127-2
- Yavari A. A geometric theory of growth mechanics // Journal of Nonlinear Science. – 2010. – Vol. 20, no. 6. – P. 781–830. DOI: 10.1007/s00332-010-9073-y
- Sozio F., Yavari A. Nonlinear mechanics of surface growth for cylindrical and spherical elastic bodies // Journal of the Mechanics and Physics of Solids. – 2016. – Vol. 98. DOI: 10.1016/j.jmps.2016.08.012
- Sozio F., Yavari A. Nonlinear mechanics of accretion // Journal of Nonlinear Science. - 2019. – Vol. 29, iss. 4. – P. 1813–1863. DOI: 10.1007/s00332-019-09531-w
- Zurlo G., Truskinovsky L. Printing Non-Euclidean Solids // Physical Review Letters. – 2017. – Vol. 119. DOI: 10.1103/PhysRevLett.119.048001
- Нестационарные колебания дискретно наращиваемого термоупругого параллелепипеда / А.Л. Левитин, С.А. Лычев, А.В. Манжиров, М.Ю. Шаталов // Изв. РАН. МТТ. – 2012. – № 6. – С. 95–109.
- Лычев С.А., Марк А.В. Осесимметричное наращива-ние полого гиперупругого цилиндра // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. – 2014. – Т. 14. – С. 209–226.
- Lychev S.A., Manzhirov A.V., Bychkov P.S. Discrete and continuous growth of deformable cylinder // In: Transactions on Engineering Technologies: World Congress on Engineering, 2015.
- Lychev S., Koifman K. Nonlinear evolutionary problem for a laminated inhomogeneous spherical shell // Acta Mechanica, 2019. – Vol. 230, iss. 11. – P. 3989–4020. DOI: 10.1007/s00707-019-02399-7
- Лычев С.А., Койфман К.Г. Геометрические аспекты теории несовместных деформаций простых структурно неод-нородных тел переменного материального состава // Дальневост. матем. журн. – 2017. – Т. 17, № 2. – С. 221–245.
- Non-Euclidean Geometry and Defected Structure for Bodies with Variable Material Composition / S.A. Lychev, G.V. Kostin, K.G. Koifman, T.N. Lycheva // J. Phys.: Conf. Ser., 2019. – Vol. 1250. – 012035. DOI: 10.1088/1742-6596/1250/1/012035
- Abraham R., Marsden J.E., Ratiu T. Manifolds, tensor analysis, and applications. – Springer Science & Business Media, 2012. – 666 p.
- Dautray R., Lions J.L. Mathematical Analysis and Numerical Methods for Science and Technology. Vol. 5. Evolution Problems I. – New York: Springer, 2000. DOI: 10.1007/978-3-642-58090-1
- Modeling and optimization of layer-by-layer structures / S.A. Lychev, G.V. Kostin, K.G. Koifman, T.N. Lycheva // J. Phys.: Conf. Ser. – 2018. – Vol. 1009. DOI: 10.1088/1742-6596/1009/1/012014
- Lychev S.A. Geometric aspects of the theory of incom-patible deformations in growing solids // In book: Mechanics for Materials and Technologies / Eds.: Holm Altenbach, Robert V. Goldstein, Evgenii Murashkin. – Springer International Publishing, 2017. – P. 327–347. DOI: 10.1007/978-3-319-56050-2_19
- Седов Л.И. Механика сплошной среды. Т. 1. – М.: Наука, 1970. – 492 с.
- Лурье А.И. Нелинейная теория упругости. – М.: Наука, 1980. – 512 с.
- Rivlin R.S. Large elastic deformations of isotropic materials, I Fundamental concepts // Phil. Trans. Roy. Soc. Lond. A 240, 1948. – P. 459–490.
- Truesdell C., Noll W. The Non-Linear Field Theories of Mechanics. – Springer Science & Business Media, 2013. – 627 p.
- Лурье А.И. Пространственные задачи теории упругос-ти. – М.: ГИТТЛ, 1955. – 491 c.
- Новацкий В. Теория упругости. – М.: Мир, 1975. – 256 с.


