Нелинейная задача оптимального управления для одной системы с параболическим уравнением при наличии нескольких подвижных источников
Автор: Юлдашев Т.К.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 1 т.17, 2016 года.
Бесплатный доступ
Во многих задачах нелинейного оптимального управления процессом теплопередачи часто приходится учитывать вспомогательные элементы, без которых невозможно управлять исследуемым процессом. Эти элементы обычно имеют сосредоточенные параметры. Поведение таких систем в общем случае описывается совокупностью нелинейных обыкновенных дифференциальных уравнений и параболических уравнений при начальных и граничных условиях. Изучены вопросы аналитического и приближенного решения подвижной точечной задачи нелинейного оптимального управления для одной системы с параболическим и обыкновенным дифференциальными уравнениями при наличии нескольких подвижных источников. При этом параболическое уравнение рассмотрено с начально-нелокальными условиями, а обыкновенное дифференциальное уравнение - с начальным условием. Отличительной чертой данной работы является то, что задание нелокальных граничных условий относительно второй переменной в параболическом уравнении упрощает процедуру применения метода Фурье разделения переменных. Функционал качества имеет нелинейный вид и дополнительно зависит от квадрата решения обыкновенного дифференциального уравнения. Сначала доказано, что функция состояния принадлежит классу соболевских функций. На основе принципа максимума сформулированы необходимые условия нелинейной оптимальности управления. Определение оптимальной управляющей функции сведено к сложному функционально-интегральному уравнению, решение которого состоит из решения отдельно взятых двух уравнений: нелинейных функциональных уравнений и нелинейных интегральных уравнений. При доказательстве однозначной разрешимости интегральных уравнений применен метод последовательных приближений в сочетании его с методом сжимающих отображений. В качестве итераций взят итерационный процесс Пикара. Получена формула для приближенного вычисления подвижного нелинейного оптимального управления и оценка для допускаемой погрешности по оптимальному управлению. Приведены формулы для приближенного вычисления нелинейного оптимального процесса и минимального значения функционала качества. Полученные результаты могут найти дальнейшее применение в развитии математической теории нелинейного оптимального управления системами с распределенными параметрами при наличии подвижных источников.
Параболическое уравнение, подвижная точечная задача, необходимые условия оптимальности управления, нелинейность управления, минимизация функционала
Короткий адрес: https://sciup.org/148177526
IDR: 148177526 | УДК: 519.
Текст научной статьи Нелинейная задача оптимального управления для одной системы с параболическим уравнением при наличии нескольких подвижных источников
Введение. Математическое моделирование многих процессов, происходящих в реальном мире, приводит к изучению прямых и обратных задач для уравнений в частных производных, не имеющих аналогов в классической математической физике. Теория смешанных задач для уравнений в частных производных в силу ее прикладной важности в настоящее время является одним из важнейших разделов теории дифференциальных уравнений в частных производных.
Одним из классов качественно новых задач для дифференциальных уравнений в частных производных являются нелокальные задачи. Нелокальные задачи в виде интегральных условий встречаются при математическом моделировании явлений различной природы, в случае, когда граница области протекания процесса недоступна для непосредственных измерений. Примером могут служить задачи, возникающие при исследовании диффузии частиц в турбулентной плазме, процессов распространения тепла, процесса влагопереноса в капиллярно-пористых средах.
С другой стороны, теория оптимального управления для систем с распределенными параметрами получила бурное развитие. К системам с распределенными параметрами относятся задачи аэрогазодинамики, химических реакций, диффузии, фильтрации, процессов горения, нагрева и т. д. [1-7].
Разрабатываются эффективные численные методы и программные средства для решения задач динамики и управления. При приближенном решении задач оптимального управления системами с распределенными параметрами используется широкий спектр разных методов (см. [8-15]).
Одним из направлений теории оптимального управления системами с распределенными параметрами является разработка методов решения задач оптимального управления при наличии подвижных источников [16]. Во многих задачах нелинейного оптимального управления процессом теплопередачи часто приходится учитывать вспомогательные элементы, без которых невозможно управлять процессом. Эти элементы обычно имеют сосредоточенные параметры. Поведение таких систем в общем случае описывается совокупностью нелинейных обыкновенных дифференциальных уравнений и параболических уравнений при начальных и граничных условиях.
В данной работе рассматриваются вопросы аналитического и приближенного решения нелинейной задачи оптимального управления для одной системы с параболическим и обыкновенным дифференциальными уравнениями при смешанных и начальном условиях и с квадратичным критерием оптимальности. При этом предполагается существование нескольких подвижных точечных источников.
Постановка задачи. Рассмотрим в области D нелинейную задачу управления процессом распространения тепла по стержню конечной длины
5 u ( t , x ) 5 2 u ( t , x ) m
' = / 2 + £ 5 ( x "° k ( t ) ) fk ( t , P k ( t ) ) (1)
5 t 5 x при начальном u (t,x)\t =o = P (x)
и нелокальных условиях l
u(t,x)|x=0 = 0, Ju(t,y)dy = 0,(3)
o где fk (t, pk ) e N(DT xQ) - функции внешнего источника; pk (t)e N(DT) - управляющие функции, k = 1, m ; u (t, x) - функция состояния управляемого процесса; р (x) - функция распределения тепла по стрежню в начальный момент времени, р(x)| x=0 = 0, р(x) eN3(Dl); §(x-°k (t)) - дельта-функция Дирака, k = 1, m; D = DT x Dl, DT = [ 0, T ]; Q = [0, M *], 0 < M *<*; Dl =[ 0, l ]; 0 < T < /, 0 < l < ro .
Функции ° k ( t ) e C ( DT ) описывают изменения положения подвижных точечных источников в пределах от нуля до l и определяются как решение следующей задачи Коши:
° k '( t ) = q k ( t , ° k ( t ) ) , ° k (0) = ° 0 = const, (4) где qk ( t , ° k ) e C 0,1 ( DT x Dl ), k = 1, m .
В данной работе при фиксированных управлениях dk ( t ) используется метод разделения переменных, основанный на поиске решения смешанной задачи (1)-(3) в виде ряда Фурье
Как и в работе [13], можно убедиться, что решение смешанной задачи (1)-(3) при фиксированных значениях управлений с помощью ряда Фурье (5) представляется в следующем виде:
где b i ( x ) =
X
U ( t , x ) = S « ( t ) • b i ( x ), (5)
i =1
2 • i i 2 i л — sin X i x , X i =----
i — 1, 2, ...
Vх I
u ( t , x ) = S l® i ( t ) + i =1 I
t m
+ J G i ( t , ^ ) S b i ( ° k
0 k =1
( s ) ) fk ( s , P k ( s ) ) ds C b i ( x ),
Задача . Найти такие управляющие функции
Pk (t) e|Pk :| Pk (t)| < M*, k = 1, m , t e DT и соответствующее им состояние u (t, x) - решение смешанной задачи (1)-(3), что доставляют минимум функционалу
J [ P ] = J [ u (T, y) -^(У) ]2 dy + m Tm
+ « SJ p k ( t ) dt +p SJ ° k ( t ) dt , k =1 0 k =1 0
где ^ ( x ) - заданная функция такая, что
X
= S^bi ( x), ^i=J^ (У) bi( y) dy, ^ (0) = 0, i=10
P = const.
В работе на основе принципа максимума
^ ( x ) =
0 < а, форму-
2. 2,.
где to , .( t ) = ф ;е x' ; G; ( t , s ) = e M ’; Ф i = J ф ( y ) b i ( y ) dy .
Предположим, что нелинейные функции fk ( t , Pk ( t ) ) удовлетворяют следующим условиям:
fk ( t , P k ( t ) )e Bnd( M k 0),0 < M k = const; (8)
fkp ( t , P k ( t ) ) * 0, (9)
e 5 fk (t, Pk (t)) , X- где fkp (t,Pk (t)) =------7----------, k = 1,m .
V 5 P k
Теорема 1. Пусть ф(x) e L2(Dl) и функции fk (t, Pk (t)), k = 1, m удовлетворяют условиям (8), (9).
Тогда для функции (7) справедливо u (t, x) e H (D) . Доказательство. Действительно, имеем лируются необходимые условия оптимальности, вычисляются управляющие функции и решается соответствующая смешанная задача (1)-(3). Данная работа является дальнейшим развитием работы [17].
Смешанная задача (1)-(3).
Обозначим
T 1
JJ u 2( t , y ) dydt < 0 0
C U ’2( D ) = | u ( t , x ): u e C 1, 2 ( D ),
Г u ( t ,0) = 0, J u ( t , y ) dy = 0 • .
Замыкание этого пространства по норме
T 1 x t m
< JJ i S ® i ( t ) + J G i ( t , s ) S b i ( ° k ( s ) ) 0 0 [ i =1 L 0 k =1
X f k ( s , P k ( s ) ) ds
I 2
• b i ( y ) Г dydt <
н ( D )
Г Г. i2 Г = < j u ( t , x ) dt -
Г) J
1 2
X
< 2
T
J
X X m®i(t>T+2 s[®i(t>]
^ i =1 ( i =1
X
) 2
X
обозначим H ( D ).
Для числовой последовательности ф i в пространстве 1 2 используется следующая норма:
x 4 m_ x
S J G ( t , s ) S b i ( ° k ( s ) ) fk ( s , P k ( s ) ) i =1 _ 0 k =1
d s
^ 2
+
I I 2
II ф1 L 2 =i S |ф d г <х
I i =1 J
Кроме того, в данной работе используются следующие обозначения. Класс функций, ограниченных по норме числом M , обозначим через Bnd( M ). Класс функций, удовлетворяющих условию Липшица по переменным u , 9 ,... с коэффициентом N , обозначим через Lip { N^u 9 j . А для функций одной переменной индекс опускается.
t
+ S J G i ( t , s ) S b i ( ° k ( s ) ) fk ( s , P k ( s ) ) ds i =1 [ 0 k =1
< 2TM 2 + 4 V2 T 2 S M°k M1 M 2 M3 + k=1
. Г m A ) 2
+ 4 T 3I S M°kM 2 M 3 I
I k =1 J
где
M 1
x 2
S mm D x Ь( t > 1 i =1 1
II ®( t ) I I s 2 ( T )
dt <
M 2 =1 l G ( t , ^ )| L 2 ( T ) ,
M 3 =| | b ( ст k ( t ) )| ^ ( T ) , k = 1, m.
Отсюда следует утверждение теоремы. И при этом нетрудно убедиться, что при выполнении условий этой теоремы функция (7) является единственным обобщенным решением смешанной задачи (1)-(3) при фиксированных значениях функций pk (t), ст k (t), k = 1, m.
Построение оптимального управления. Пусть p k ( t ) являются оптимальными управлениями
А J [pk (t) ] = J[Pk (t) + АPk(t) ]- J [Pk(t) ]^ 0, где pk (t) + Аpk (t) € H(DT), k = 1, m .
Нетрудно показать, что применение принципа максимума приводит к следующим необходимым условиям оптимальности [4]:
9 ( t , ст k ( t )) fkp ( t , Pk ( t ) ) - 2 a Pk ( t ) = 0, (10)
9 ( t , ст k ( t )) fkPp ( t , p k ( t ) )- 2 a < 0, k = 1, m , (11)
где 9 ( t , x ) - обобщенное решение следующей задачи:
9 1 ( t , x ) +9 xx ( t , x ) = 0, ( t , x ) € D ,
9 ( t , x ) = - 2 [ u ( T , x ) -^ ( x ) ] ,
l
9 (t,0) = 0, J9 (t, y) dy = 0, сопряженной с задачей (1)-(3), и определяется по формуле
T m
х
9 ( t , x ) = - 2 £ ® i ( T ) + J G i (T , S ) £ b i ( ст k ( s ) ) x i =1 L 0 k =1
X fk ( s , P k ( s ) ) ds - i G i ( T , t ) b i ( x ) .
С учетом условий (8), (9) условия оптимальности (10), (11) перепишем в следующем виде:
2 a P k ( t ) f ^C t , P k ( t )) = 9 ( t , ст k ( t )), (13)
fkP ( t , Pk ( t )) , Pk ( t ) ... > 0, k = 1, m .
I fkp ( t , Pk ( t )) J
С учетом (14) из (12) и (13) получаем a Pk (t) fkp(t, Pk (t)) + х T m
+ £ J G i ( T , t ) G i ( T , s ) £ b 2 ( ст k ( s ) ) fk ( s , P k ( s ) ) ds = i =1 0 k =1
х
= £ ( ® i ( T ) + ^ i ) G i ( T , t ) b i ( ст k ( t ) ) i =1
или mT aPk(t) fit-1(t, Pk(t))+£J Q(t, s)fk(s, Pk(s)) ds=F(t),(15)
k =1 0
где
х
Q(t,s) = £G(T, t) Gi(T, s)Ь2(стk (s)), i=1
х ___
F ( t ) = £ ( ® i (T ) .. ) G i ( T , t ) b i ( ст k ( t ) ) , k = 1, m .
i =1
В уравнение (15) положим aPk(t) fk-1(t, Pk(t)) = gk(tX k = 1,m, где gk (t) - пока неизвестные функции, но мы для начала предположим, что они заданы. Тогда имеем следующие функциональные уравнения:
P k ( t ) = g k^ t ) f kp ( t , P k ( t )), k = 1, m . (16)
a
Пусть выполняется следующее условие:
fkp (t,Pk(t) )€ Bnd(M1)nLip) N 1|pk ), k = 1,m , 0 < N 1, M 1 = const.
Тогда функциональные уравнения (16) имеют единственное решение, которое на отрезке DT находится из следующего итерационного процесса:
p n + 1( t ) = g k^ t ) f kp ( t , p k ( t )), k = 1? m , n = 1, 2,... (17) a
Это решение обозначим так:
P k ( t ) = h k ( t , g k ( t )), k = 1, m . (18)
Теперь для определения функции gk (t), подставляя (18) в (15), получаем интегральные уравнения Фредгольма mT gk(t)+£J Q(t, s) fk (s, hk (s, gk(s))) ds=F(tx k=1, m.(19) k =10
В качестве нормы для произвольной функции V ( t ) е C ( DT ) используем евклидову норму
II V ( t )| l c = max |V ( t )|- t € D T
Теорема 2. Пусть:
-
1) Выполняются условия теоремы 1 и условие (14);
-
2) ^ ( x ) € L 2 ( D i );
-
3) h k ( t , g k ( t ) )е Bnd( M k 1 ) n Lip ) N k 1\gk } ,
0 < N k 1 , M k 1 = const;
-
4) f k ( t , h k ( t ) ) € Bnd( M k 2 ) n Lip ) N k 2 I gk } ,
0 < N k 2 , M k 2 = const;
-
5) p = ( M 2 M 3 ) T £ N k 1 N k 2 < 1.
k =1
Тогда нелинейные интегральные уравнения Фредгольма второго рода (19) имеют единственное решение g k ( t ) е C ( D t ).
Доказательство . Сначала заметим, что функции Q ( t , 5 ) и F ( t ) ограничены
I Q ( t , 5 )| 2 \ОДТ , t ) b . ( ° k ( t )) < i =1
i2
2;Jax|G,(T,t)| x I=1
I I 2.2
x 2 max bi ( ° ( t )) = ( MM ) <m ; t е Dt' m
I F ( t )| <A - E|M T ) + ^|| G ( T , t )| <
’ l i =1
m m.^2
<£ 2 “ . ( T ) +5 . ! 2 G ( T . t )|2
V 1 M=1 J I i =1
<
< ^ ( M 1 +^l k ) M 2 <m .
С учетом оценок (20) и (21) рассмотрим следующий итерационный процесс:
m Т gk(t)+ZJQ (t,5) fk (5, hk (5,0))d5=F (t), k =10
mT
Vk ( t ) + £j Q ( t , 5 ) fk ( 5 , h k ( 5 , g k ” ( 5 ) ) ) d5 = F ( t ), (22)
k =10
n = 1, 2,...
||gk ( t ) - g k ”( t )|| C <
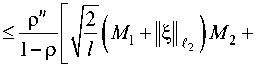
m
(M2 M3 ) 2 2 Mk 2 Т k =1
Отсюда с учетом (18) и второго условия теоремы 2 для погрешности приближенного вычисления управляющих функций получаем оценку
I P k ( t ) - P n ( t )|| C <
< Г - П р[ И ( M 1 +И1 -2 ) M 2 + m m
+ ( M 2 M 3 ) 2 M k 2 T 2 N k 1 . k =1 J k =1
Построение оптимального процесса и вычисление минимального значения функционала. Согласно (7) оптимальный процесс находим по формуле
m
u(t, х) = 2i®.(t)+2J G.(t,5)b. (° k(5) )x i=1 l k =10
x fk ( 5 , P k ( 5 ) ) d5 } • b .- ( x ).
Оптимальный процесс (26) можно приближенно найти с помощью итерационного процесса Пикара nmt un (t,х)=Z1®>(t)+2J Gi(t,5) bi (° k(5 ))x i=1
x fk ( 5 , P k ”( 5 ) ) d5 ) • b i ( x ).
В силу условий теоремы из (22) получаем следующие оценки:
Минимальное значение функционала, согласно формулам (6) и (26), находится из следующей формулы:
I g k ( t >1 с
m Т
< F ( t ) - 2J Q ( t , 5 ) fk ( 5 , h k ( 5 ,0 ) ) d5
k =1 0
<
C
J [ P k ] = J
m m T
2Ui(Т) + 2JG.(T,5)b.(°k (5))x i=1 k =1 0
< 2 ( M 1 +|^|| ) M 2 + ( M 2 M 3 ) 2 2 M 2 T < m ; (23) ’ l k =1
I g k “( t ) - g k ( t )|| с <
< 2 J Q (t•5 >i|If (5, h« (5, sk <5 >))- k =1 0
- fk ( 5 , h k ( 5 , g k - 1( 5 ) ))|| ^5 <
< ( M 2 M з ) 2 T \k 2 11 h k ( 5 , g k ( 5 ) ) " h k ( 5 , g k - 1 ( 5 ) ) J < k =1 C
g
k
” (
t
)
-
g
k
-
1 (
t
)||
C
< ||
g
k
” (
t
)
-
g
k
-
1 (
t
)||
C •
(24)
Из оценок (23) и (24) следует, что нелинейные интегральные уравнения Фредгольма второго рода (19) имеют единственное решение
gk
(
t
)
е
C
(
Dt
),
k
=
1,
m
. Теорема доказана.
Кроме того, из (19) и (22) аналогично (23) и (24) можно получить, что справедлива оценка x
fk
(
5
,
P
k
(
5
)
)
d5
-
^t
[•
b
.
(
y
)
dy
+
m T
2
m T
+
a
2j
(
p»
(
t
)
)
dt
+₽
SJ
(
°
k
(
t
)
)
dt
. (28)
k
=1 0
k
=1 0
Из работы [18], в частности, следует, что задача Коши (4) при выполнении условия 4k (t, ° k (t) )е Bnd(M 4) n Lip{N 3|° k }, k = 1, m, 0 < M 4, N 3 = const имеет единственное решение °k (t) е C (Dt ), k = 1, m .
Теорема 3
.
Пусть выполняются условия теоремы 2. Тогда функционал (28) принимает конечное значение.
Доказательство.
Учитывая доказательства теорем 1 и 2, из (28) получаем
J
[
P
k
]
<
2
(
M
1
+KI I-
2
)
2
+
(
\ m
2
M
1 +hlk )
2
M
k
(
M
2
M
3
)
+
' k
=1
(
)2 _.\2
+
2T
2
I
£
M
^
M
2
M
3
I + a
T
(
mM
*
)
+ Р
Tm
2
l
2
<»
.
к
k
=1
J
Отсюда следует, что функционал (28) принимает конечное значение. Теорема доказана. Приближенное значение функционала вычисляется по следующему итерационному процессу: l mT n nm
J
[
Р
П
]
=
J Е
1
®
-
(
T
)
+
Я
G
i
(T
,
5
)
bi
(
a
k
(
5
)
)
x
k
=1 0
X f ( 5, pk( 5)) dS-Ц- b-( y) dy + m T 2 m T 2
+ a
£j
(
P
k
(
t
)
)
dt
+ P
£j
(
a
k
(
t
)
)
dt
,
n
=
1,2,3,...; (29)
k
=1 0
k
=1 0
a
k
(
t
),
k
=
1,
m
определяется из следующего итерационного процесса:
t ak' (t) = CTk + Jqk (5, ak (5)) d5, k = 1, m. (30)
Заключение.
В работе предлагается методика решения одной точечной подвижной задачи нелинейного оптимального управления для одной системы с параболическим и обыкновенным дифференциальными уравнениями при смешанных нелокальных и начальном условиях. Сначала используется метод Фурье разделения переменных. На основе принципа максимума формулируются необходимые условия оптимальности управлений при квадратичных критериях. Доказывается однозначная разрешимость оптимальных управлений. При этом используется метод последовательных приближений в сочетании его с методом сжимающих отображений. Получается формула для приближенного вычисления подвижных оптимальных управлений и оценка для допускаемой погрешности по оптимальным управлениям. Приводятся формулы для приближенного вычисления оптимального процесса и минимального значения функционала. При этом используются итерационные процессы (17), (22), (27), (29) и (30). Полученные результаты могут найти дальнейшее применение в развитии математической теории нелинейного оптимального управления системами с распределенными параметрами при наличии подвижных источников.
Список литературы Нелинейная задача оптимального управления для одной системы с параболическим уравнением при наличии нескольких подвижных источников
- Бутковский А. Г. Теория оптимального управления системами с распределенными параметрами. М.: Наука, 1965. 474 с.
- Евтушенко Ю. Г. Методы решения экстремальных задач и их применение в системах оптимизации. М.: Наука, 1982. 432 с.
- Егоров А. И. Оптимальное управление тепловыми и диффузионными процессами. М.: Наука, 1978. 464 с.
- Керимбеков А. Нелинейное оптимальное управление линейными системами с распределенными параметрами: дис.. д-ра физ.-мат. наук. Бишкек: Ин-т математики НАН Кыргызской Республики, 2003. 224 с.
- Лионс Ж. Л. Оптимальное управление системами, описываемыми уравнениями с частными производными. М.: Мир, 1972. 412 c.
- Лурье К. А. Оптимальное управление в задачах математической физики. М.: Наука, 1975. 480 c.
- Рапопорт Э. Я. Оптимальное управление системами с распределенными параметрами. М.: Высш. шк., 2009. 680 с.
- Кротов В. Ф., Гурман В. И. Методы и задачи оптимального управления. М.: Наука, 1973. 448 c.
- Миллер Б. М., Рубинович Е. Я. Разрывные решения в задачах оптимального управления и их представление с помощью сингулярных пространственно-временных преобразований//Автомат. и телемех. 2013. № 12. С. 56-103.
- Срочко В. А. Итерационные методы решения задач оптимального управления. М.: Физматлит, 2000. 160 с.
- Тятюшкин А. И. Численные методы и программные средства оптимизации управляемых систем. Новосибирск: Наука, 1992. 193 с.
- Федоренко Р. П. Приближенное решение задач оптимального управления. М.: Наука, 1978. 488 с.
- Юлдашев Т. К. Приближенное решение нелинейного параболического и обыкновенного дифференциального уравнений и приближенный расчет функционала качества при известных управляющих воздействиях//Проблемы управления. 2014. № 4. С. 2-8.
- Юлдашев Т. К. О построении приближений для оптимального управления в квазилинейных уравнениях с частными производными первого порядка//Матем. теория игр и её прилож. 2014. Т. 6, № 3. С. 105-119.
- Юлдашев Т. К. Приближенное решение точечной подвижной задачи оптимального управления для нелинейного гиперболического уравнения//Моделирование и анализ информационных систем. 2014. Т. 21, № 3. С. 106-120.
- Бутковский А. Г., Пустыльников Л. М. Теория подвижного управления системами с распределенными параметрами. М.: Наука, 1980. 384 с.
- Юлдашев Т. К. Нелинейная точечная задача оптимального управления для псевдопараболического уравнения//Вестник ВоронежГУ. Сер. «Системный анализ и информационные технологии». 2014. № 3. С. 9-16.
- Юлдашев Т. К. Развитие теории нелинейных дифференциальных уравнений с максимумами: дис.. канд. физ.-мат. наук. Бишкек: Ин-т математики НАН Кыргызской Республики, 1993. 121 с.
- Butkovskiy A. G. Teoriya optimal’nogo upravleniya sistemami s raspredelyonnymi parametrami . Мoscow, Nauka Publ., 1965, 474 p. (In Russ.).
- Evtushenko Yu. G. Metody resheniya ekstremal’nykh sadach i ikh primeneniye v sistemakh optimizatsii . Мoscow, Nauka Publ., 1982, 432 p. (In Russ.).
- Egorov А. I. Optimal’noye upravleniye teplovymi i diffuzionnymi protsessami . Мoscow, Nauka Publ., 1978, 464 p. (In Russ.).
- Kerimbekov А. Nelineynoye optimal’noye upravleniye lineynymi sistemami s raspredelyonnymi parametrami. Dis. d-ra fiz.-mat. nauk. . Bishkek, Inistitut matematiki NAN Kyrgyzskoy Respubliki Publ., 2003, 224 p. (In Russ.).
- Lions J. L. Optimal’noye upravleniye sistemami, opisyvayemymi uravneniyami s chastnymi proizvodnymi . Мoscow, Mir Publ., 1972, 412 p. (In Russ.).
- Lur’ye К. А. Optimal’noye upravleniye v zadachakh matemsaticheskoy fiziki . Мoscow, Naukа Publ., 1975, 480 p. (In Russ.).
- Rapoport E. Ya. Optimal’noye upravleniye sistemami s raspredelyonnymi parametrami . Мoscow, Vysshaya shkola Publ., 2009, 680 p. (In Russ.).
- Кrotov V. F., Gurman V. I. Мetody i zadachi optimal’nogo upravleniya . Мoscow, Naukа Publ., 1973, 448 p. (In Russ.).
- Miller B. M., Rubinovich E. Ya. Discontinuous solutions in the optimal control problems and their representation by singular space-time transformations. Automation and Remote Control. 2013, Vol. 74, No 12, P. 1969-2006.
- Srochko V. А. Iteratsionnye metody resheniya zadach optimal’nogo upravleniya . Мoscow, Fizmatlit Publ., 2000, 160 p. (In Russ.).
- Tyatyushkin А. I. Chislennye metody i programmnye sredstva optimizatsii upravlyaemykh sistem . Novosibirsk, Naukа Publ., 1992, 193 p.
- Fedorenko R. P. Priblizhennoe reshenie zadach optimal’nogo upravleniya . Мoscow, Naukа Publ., 1978, 488 p. (In Russ.).
- Yuldashev T. K. . Problemy upravleniya. 2014, No 4, P. 2-8 (In Russ.).
- Yuldashev Т. К. . Matematicheskaya teoriya igr i eyo prilozheniya. 2014, Vol. 6, No 3, P. 105-119 (In Russ.).
- Yuldashev T. K. . Modelirovanie i analiz informatsionnykh sistem. 2014, Vol. 21, No 3, P. 106-120 (In Russ.).
- Butkovskiy A. G., Pustyl’nikov L. M. Teoriya podvizhnogo upravleniya sistemami s rasprederlyonnymi parametrami . Moscow, Nauka Publ., 1980, 384 p. (In Russ.).
- Yuldashev Т. К. . Vestnik VoronezhGU. Seriya: Sistemnyi analiz i informatsionnyie tekhnologii. 2014, No 3, P. 9-16 (In Russ.).
- Yuldashev T. K. Razvitie teorii nelineynykh differentsialnykh uravneniy s maksimumami. Diss. kand. fiz.-mat. nauk. . Bishkek, Institut matematiki NAN Kyrgyzskoy Respubliki Publ., 1993, 121 p. (In Russ.).


