Нелинейное деформирование ортотропной мембраны, натянутой на жесткий каркас

мембраны регламентируется. Величина прогиба при заданной нагрузке зависит от усилия натяжения и упругих параметров мембраны.

В работе получено уравнение, связывающее между собой усилие натяжения, действующую нагрузку, геометрические и упругие параметры мембраны и прогиб в центре мембраны. Это уравнение позволяет определять требуемое усилие натяжения при заданном прогибе.

Отнесем плоскость мембраны к системе координат х, у и обозначим через а и Ъ размеры мембраны по осям х и у соответственно (рис. 3).

а х

Рис. 1. Солнечная батарея: а - каркас; б - мембрана с фотоэлементами

Рис. 3. Система координат и размеры мембраны

В процессе сборки на каркас солнечной батареи накладывается мембрана и натягивается по периметру (рис. 2).

Деформирование ортотропной мембраны описывается системой нелинейных дифференциальных уравнений, которая включает уравнения равновесия:

dN  дNxv x + ——xy = о, дx    дy

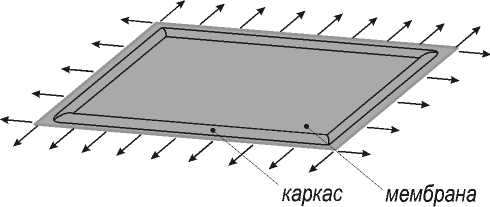
Рис. 2. Натяжение мембраны

- N XCx xx

^^^^^^в

N у х * xy Л xy

д N  д N

—xy - + — y- = 0 , д x    д y

^- N y X y ⁺ Р = ⁰,

физические соотношения

^Nx = А1^е x ^{+ В}12 ^е y ⁺ T x ,

N y = ^В 12 ^е x ⁺ B 22 ^е y ⁺ T y ,

N xy ^— B 33 ^е xy , геометрические соотношения:

ди 1 f д w V еx дx + 2(дxJ ’y ди д v

д v 1 f д w ^ = з— + - —

д y 2 (д y

,

После натяжения мембрана закрепляется на каркасе, и к ней крепятся пластины фотоэлементов. При выведении космического аппарата на орбиту, во время раскрытия солнечной батареи на мембрану действует распределенная нагрузка, равная произведению погонного веса фотоэлементов и полотна мембраны на перегрузку. Под действием этой нагрузки мембрана прогибается. При проектировании конструкции солнечной батареи прогиб

. д w д w

е —11, y  дy  дx  дx дy

„ _ д2w д2w „  - э д2w х x    дx2 , Х y дy2 , Х xy 2 дx дy

^^^^^^в

.

В уравнениях (1), (2), (3) A ., A ,, Д' - мембранные усилия; е _x , е _y , е , - мембранные деформации; % _х , % ^ , % -изменение кривизны и кручение плоскости мембраны; и , v - перемещение мембраны по осям х и у соответ-

ственно; w - прогиб мембраны; В ₁₁ , В ₁₂ , В ₂₂ , В ₃₃ - мембранные жесткости; р - давление, действующее на мембрану; Т , , Т , - усилия натяжения мембраны вдоль осей х и у соответственно.

Получим разрешающую систему уравнений, содержащую в качестве неизвестных перемещения и , v , w . Последовательно подставляя (2) и (3) в (1), получим:

д ² и      д ² и             д ² v      д w д ² w

В     + В₃₃     + ( В- + В ₃ ) + В +

¹¹ д х ^{2    33} д у ^{2      2 33} д х д у    ¹¹ д у д х д у

+ (В'- + В33) £ £w + В33 X У? = 0- ду дхду      дх ду 2

4             22      4

c 22 = 3[3 B n ^4 + 2(3 B 12 - 2 В 33 ) ^2 ^2 + 3 В - ^y ]. a           ab b

По уравнениям (6) найдем

= - ^b 1 ^a —  b 2 ^a 12 w ¹

^a 11 ^a 22 ^{- a} 12

b 2 ^a 11 ^- b 1 ^a 21

^, V                               2 .

^a 11 ^a 22 ^{- a} 12

Подставляя (9) в (7), получим c 33W3 + cnW - p -2- = 0,           (10)

п

где

( B 2 + В ₃ з) ^ и + B₃₃ Ц + B₂₂     + B.

^{12    33} д х д у     33 д х ^{2     22} д у³¹     "

д w д ² w

'33 д у д х

. 2 +

B 11

⁺ B 12

_r , ^b 1 ^{( a} 22 ^c 12 ^{- a} 21 ^c 21 ) ^{+ b} 2 ^{( a} 11 ^c 21 ^{- a} 12 ^c 12 )

c 33 = ^c 22 ⁺                            2

^a 11 ^a 22 ^{- a} 12

+ ( в„ + в, ,) 2 w 22 w + в₂₂ 2 w    = 0,

12     33                   22                 , дх дхду      ду ду2

2        2         2222

д и д w  „ д и д w  1 „ ( д w ' д w  1 „ ( д w 'д

+ В12        +-B11I           +-В12| дх дх2 дх ду2   2 I дх J дх2   2 I дх Jд

2                2                    22

д v д w „  д v д w 1 „ ( д w ' д w 1 „ ( д w ' д w

+ В-,-, +    В- I + В-, +

■ д у д х ²        д у д у ²   2 I д у I д х ²   2 I д у I д у ²

Кубическое уравнение (10) является основным для рассматриваемой задачи. Оно связывает между собой усилия натяжения Т, , Т, , действующую нагрузку р , размеры мембраны а , b , упругие параметры В ₁₁ , В ₁₂ , В ₂₂ , В ₃₃ и прогиб в центре мембраны W . Рассмотрим некоторые

д и д ² w        д v д ² w        д w д w д ² w

+ 2 В33--+ 2 В33--+ 2 В33---+ ду дхду      дх дхду       дх ду дхду

+ Г , — + T_v — + P = 0.

^х д х ^{2 у} д у у

Удовлетворяя граничным условиям, предполагающим отсутствие перемещений на краях мембраны, представим решение уравнений (4) в следующем виде:

2пх . пу и (х, у) = U sin---sin —, ab

п х . 2п у

V(х, у) = V Sin — Sin---- , ab пх . пу w(х, у) = W Sin--Sin — , ab

варианты использования этого уравнения:

• -    заданы упругие и геометрические параметры мембраны, усилия натяжения и давление. По уравнению (10) определяется прогиб W . Затем, используя уравнения (9), находятся величины и и V . Равенства (5) задают распределения перемещений по поверхности мембраны. При необходимости, используя уравнения (2) и (3), можно определить мембранные усилия;

• -    заданы упругие и геометрические параметры мембраны, давление и требуемый прогиб. По уравнению (10) можно найти усилие натяжения, обеспечивающее регламентируемый прогиб.

Сделаем здесь одно замечание. Уравнение (10) получено в предположении, что перемещения мембраны могут быть с достаточной точностью представлены одним членом двойного тригонометрического ряда (5). Это

где U , V , W- неизвестные числа, подлежащие определе-

нию.

Подставляя (5) в (4) и используя процедуру Бубнова-Галеркина, получим систему нелинейных алгебраических уравнений

- a₁₁U - a₁₂V = b 1 W ² , - a ₂₁ U - a ₂₂V = b ₂W ² ,    (6)

- c 11 W + c ₁₂ UW + c₂₁VW - c₂₂W ³ + p ¹⁵3⁶ = 0 . (7) п ²

Здесь

_,. _ п2    _ п2.                                    . 1

a11 = 9(4B11” + B33 72") , a12 = a21 = 64(B12 + B33)—7 , a2       b2                             ab пп a22 = 9(4B22 72" + B33 “T) , b2 a2

b1 = 6[2B11 ^-(B12 -B33)], a      a2

b 2 = 6[2 В - ^y-(B12 - В 33) ^y ],(8)

b      b2

допущение может считаться справедливым для несильно вытянутых мембран. Для солнечных батарей каркас проектируется таким образом, что отношение а / b не превышает 2. Поэтому уравнение (10) вполне может быть использовано для определения параметров напряженно-деформируемого состояния мембраны, особенно на этапе проектных расчетов.

В качестве примера получим разрешающее уравнение (10) для изотропной квадратной мембраны, растянутой по контуру одинаковым усилием. Для такой мембраны a = b ,Тх= Ту = Т, Ви = В - = В , В12 = ВД, (12) Б33= 1-^B В = —E^h

33     2     ,      1 -д2 , где Т - усилие натяжения; h - толщина мембраны; Е -модуль упругости; Д - коэффициент Пуассона материала мембраны. Подставляя (12) в (8) и (11), после некоторых преобразований получим разрешающее уравнение (10) в следующем виде:

Eh—fW ³ + - Т — W - p  = 0 ,       (13)

a 2 a п

22        22

C11 = 96(Тх ^y + Ту п-), C12 = -8 -[2B11 ^y + (2B12 + В33)]

a2      b2          п a      a2

,    1 .4(2 + 2д + т)(2-ц + т), 3        2        1-ц где f =---у(-Ц—ц—)(—ц—)) +—(1 + ц—т));т= 1 Д .

1 -ц ² 9 п ²(4 + т ) + 64( ц + т )   64       3         2

128 п     п             п c21 =    —[2B — —у + (2B12 + B33)—y], п b      b2              a2

Преобразуем уравнение (13) к безразмерному виду. Для этого введем в рассмотрение новую функцию - безразмерный прогиб

W z = —. h

Подставляя (14) в (13), получим кубическое уравнение

3    1 о a 4 pa z +          z —         =

2 n 2 f E h ² n ⁶ f E h ⁴

где о = T / h - напряжение натяжения мембраны. По уравнению (15) следует, что безразмерный прогиб z зависит от трех величин: о / E , p / E и а / h .

Представим изменение безразмерного прогиба z в зависимости от аргументов р /Е и о /Е (рис. 4). Расчет выполнен для а/h = 1 000.

Зависимость z(р/Е,о/Е) носит нелинейный характер. По мере роста усилия натяжения влияние давления уменьшается. Отметим, что эта особенность поведения прогиба сохраняется и для ортотропной мембраны.

Таким образом, решена задача о деформировании ортотропной мембраны, натянутой на жесткий каркас. Полученные результаты могут найти применение при проектировании солнечных батарей космических аппаратов.

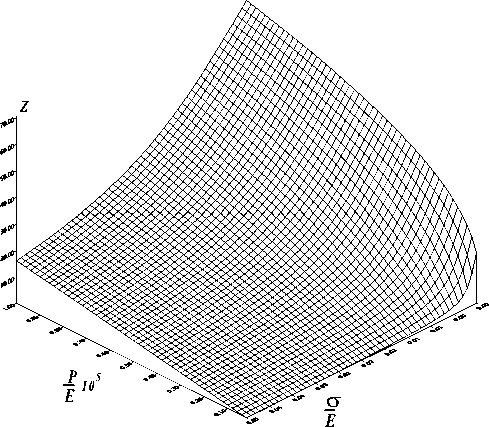
Рис. 4. Изменение безразмерного прогиба

А. V. Lopatin, L. V. Shumkova

NONLINERIAN DEFORMATION OF AN ORTHOTROPIC MEMBRANE STRETCHED ON THE FRAME

The problem of the deformation of an orthotropic membrane stretched on aframe of the solar battery is presented.