Нелинейное деформирование тонкой сферической оболочки под давлением

Сосуды высокого давления, в том числе и сферические баки, используются в аэрокосмической технике, также имеют широкое применение в быту. Если не допускаются большие деформации, тогда для решения вопроса обеспечения прочности конструкции применяется уравнение равновесия Лапласа [1] с приложением нормативных коэффициентов запаса в соответствии с назначением. Для тонкостенных сосудов давления, изготовленных из композиционных материалов, резины или иных каучуковых материалов, вопросы деформирования от действия давления, в том числе и от изменения давления при стыковке сосудов, в литературе по строительной механике приводятся недостаточно [2–3].

Формулировка задачи. Рассмотрим модель деформирования сферической оболочки. Пусть срещинная поверхность оболочки имеет первона чальный радиус R0. От действия давления q первоначальный радиус оболочки увеличивается на величину w, которую назовем прогибом. Составим уравнение равновесия по деформированной схеме, из которого вычислим внутреннее мембранное усилие

N = q (R о + w)

Положим упругое деформирование материала в рамках закона Гука [4]:

w

£ =

R 0

.

Допуская равномерное распределение напряжения σ по толщине t , имеем

Нелинейное деформирование тонкой сферической оболочки под давлением

Объем материала оболочки вычислим по формуле

V m = 4 n R 00 1 0 .                  (5)

Здесь t ₀ – начальная толщина.

Учитывая, что объем материала V_m оболочки при ее деформировании не изменяется, толщина t будет величиной переменной,

V t = m-----2.

4 п ( R 0 + w )

Подставив соотношения (2)–(6) в уравнение (1), получим нелинейное уравнение, связывающее нагрузку и прогиб:

w 2 n R q

---------Г -     0 = °.            (7)

( R ° + w ) ³    EV m

Решение . Рассмотрим оболочку в виде шара с начальным радиусом R ° = 0,1 м и начальной толщиной t ₀ = 10^–3 м. Материал примем из группы каучуковых, имеющих Е = 1 МПа. Примем внутреннее давление q = 2000 Па. Для этих данных на рис. 1 покажем графическое решение уравнения (7). Из рисунка видим, что одной и той же нагрузке соответствуют три корня, из которых отрицательное значение отбрасываем. Принимаем во внимание два прогиба, равные w = 1,5-10 ² м и w = 14-10 ² м.

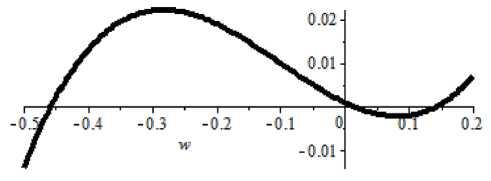
Рис. 1. График невязки нелинейного уравнения

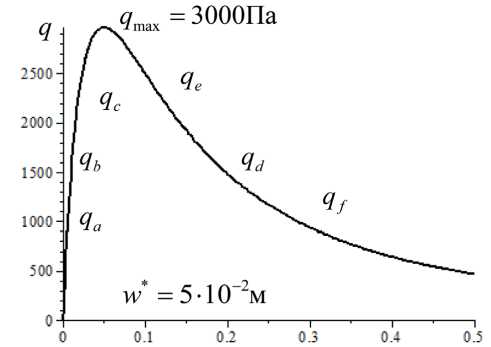
Рис. 2. График, связывающий давление и прогиб

Рассмотрим взаимосвязь прогиба с внутренним давлением, внутренним объемом шарового баллона, напряжением и толщиной стенки при условии несжимаемости материала.

Выразив из уравнения (7) давление, полу- чим

EV w q = m .

2 п R ₀ ( R ₀ + w )

Тогда из условия dq/dw = 0 получим значение максимального давления q = 2 EV m /27 п R 0 . Максимальное давление соответствует прогибу w * = R ₀/2. Изобразим функцию изменения давления (8) в области 0 ≤ w ≤ 0,5 м на рис. 2, где максимальное давление q = 3000 Па, а прогиб w * = 5"10 ² м. Из графика видно, что одной и той же нагрузке q соответствуют два значения прогиба, кроме точки w .

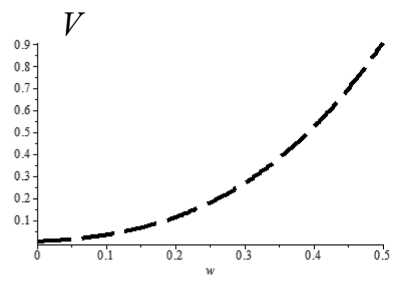
Приведем еще четыре графика на рис. 3: – увеличение внутреннего объема оболочки

V = 4п( R ₀ + w )³/3 (рис. 3, а );

• -    уменьшение толщины t = V m / 4п( R ₀ + w )² (рис. 3, б );

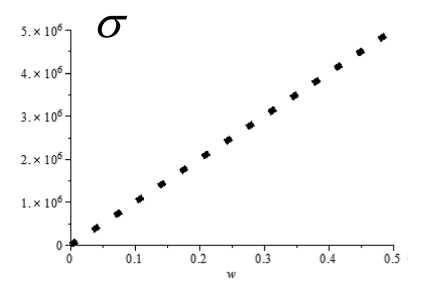
• -    изменение напряжения (рис. 3, в ), вычисляемого по формулам (2) и (3);

  – изменение внутреннего усилия, найденного по формуле (4) (рис. 3, г ).

Заметим, что напряжения в области 0 ≤ w ≤ 0,5 м не превышают значения 5 МПа, что не превосходит предела прочности резины 13–14 МПа.

Анализ решений. Рассмотрим соединяющиеся шаровые сосуды давления (рис. 4).

• 1.    Надуем два одинаковых шарика разными давлениями q_а и q_b , но не превышающими давления q _max (рис. 1). Затем шарики соединим. Давления в шариках выравниваются, и шарики приобретают одинаковый радиус.

• 2.    Если первый шарик надуть давлением q c <  q max в области w <  w * (рис. 1), а второй надуть давлением q d <  q max в области w <  w * (пусть q c >  q d ), тогда при выравнивании давления шарик меньшего диаметра раздувает шарик большего диаметра.

• 3.    Вновь одинаковые шарики надуем давлениями q e и q f (рис. 1), превышающими q max , но разными ( q e >  q f ). Шарик меньшего диаметра уменьшается, накачивая шарик большой.

Физические эксперименты по взаимодействию сообщающихся сосудов давления - воздушных шариков проведены в [5]. На рис. 4 представлены фотографии примера раздувания шарика большего диаметра шариком, который изначально имел меньший диаметр, но большее давление.

ИССЛЕДОВАНИЯ

Havko-

Ж ГРАДА

а

^ 0.0010

0.0009

0.0008-

0.0007

0.0006-

0.0005 -

0.0004-

0.0003 -

0.0002-

0.0001 -

о

0.1

OJ

0.4

0.5

в

б

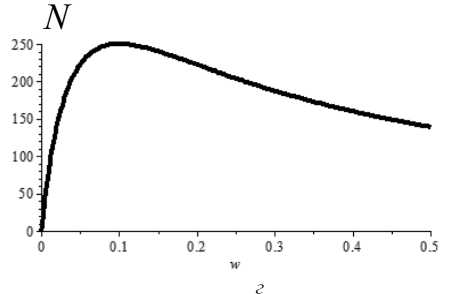
Рис. 3. Графики, характеризующие изменения переменных параметров шара: а – увеличение внутреннего объема; б – уменьшение толщины; в – изменение напряжения; г – изменение внутреннего усилия

,TiE 1

а б

Рис. 4. Фотографии раздувания шарика большего диаметра шариком, который изначально имел меньший диаметр, но большее давление

Заключение

В шаровой оболочке внутреннее давление, прогиб, внутренний объем и толщина стенки так связаны между собой, что давление увеличивается до определенного значения, затем оно начинает уменьшаться. Одному и тому же давлению соответствуют два деформированных состояния.

Вопросы деформирования тонкостенных оболочек, допускающих существенные прогибы, требуют изучения.