Нелинейное описание движения фронта реакции

Большой научный интерес представляет поиск уравнения, описывающего химическое равновесие и движение фронта химической реакции [1]. Особое внимание уделяется присущей фронту реакции (например, пламени) гидродинамической неустойчивости Дарье–Ландау (ДЛ-неустойчиво-сти), вызванной тепловым расширением газа при экзотермическом процессе [1--8]. Действительно, газообразное топливо быстро натекает и сгорает в тонком слое газа, превращаясь вследствие сильного энерговыделения в газ с существенно большей температурой (и меньшей плотностью). Для типичных углеводородных пламен скачок плотности на фронте весьма велик: 9 = p u /р ь = 5 — 10 [1]. В результате дополнительный объём газа, порожденный тепловым расширением, толкает топливо по нормали к каждой локальной точке поверхности фронта реакции, способствуя его распространению. Понимание динамики распространения реакций позволило бы глубже понять механизм их развития и обнаружить новые эффекты и явления. Уравнение фронта экзотермической реакции (горения) получено лишь в приближении слабо искривленного фронта и / или малого теплового расширения в процессе реакции [8--11]. Прямое численное моделирование подобных процессов сильно затруднено вследствие разнообразия характерных химических и гидродинамических размеров, (10 - ² -10 - 3 ) мм и (0 , 1 -1) м соответственно [6, 12].

В данной работе, вытекающей из нашей предыдущей работы [13], полная система гидродинамических уравнений, описывающих развитие гидродинамической неустойчивости фронта реакции в двумерном / трёхмерном потоке, сведена к замкнутой системе поверхностных уравнений. Данная процедура проведена с использованием переменных Лагранжа, специальных интегралов движения и их аналогов. При этом показано, что завихренность играет ключевую роль в динами- ке гидродинамических разрывов, придавая уравнениям дифференциальный вид. В изоэнтропическом приближении демонстрируется, как учесть вызванные этим движением колебания плотности жидкости, позволяющие учесть влияние звука на развитие (или затухание) ДЛ-неустойчивости. Полученная система уравнений согласуется с ранее известными аналитическими решениями, полученными в частных случаях.

• II.    Неустойчивость Дарье–Ландау в 3D-потоке

  • II.1.    Бесконечно тонкий фронт

Рассмотрим распространение бесконечно тонкого, слабо искривленного фронта реакции в трёхмерном (3D) потенциальном внешнем потоке (рис. 1). При этом u = V^ и Л ф = 0. Обозначим все величины впереди и позади фронта индексами «—» и «+» соответственно. Предположим, что газодинамика горения характеризуется пространственным масштабом R (это может быть радиус трубы, ширина двумерного канала, радиус сферической камеры сгорания и т.д.). Для удобства, аналогично работе [11], введём безразмерные величины: скорость u = v/U f , координаты r = x/R и давление P = (П — П f ) /p f U 2 , где p f и П f — соответственно плотность и давление в топливе бесконечно далеко от фронта, а U f — скорость пламени с плоским фронтом. Время t обезразмерим величиной R/U f . Течение газа предполагается несжимаемым и невязким. Тогда гидродинамические уравнения принимают вид

∂u ∂t

u x w + V ^O P + u ^) = 0 ,

∂ω dt" = V х [ u x w ], div u = 0,

где O = 1 в топливе и O = 9 = p-/p + в сгоревшем газе. Граничные условия на поверхности фронта, следующие из законов сохранения, будут выглядеть следующим образом [11]:

u + — u- = (6 — 1) n,(4)

P+ — P- = 1 — 6,(5)

V =1 — Un-,(6)

где θ — скачок плотности, n — внутренняя нормаль и V — проекция скорости фронта на отрицательное направление вектора n . Скорости u _{n -} = д^/дп = 1 — V и u _T = д^/дт связаны между собой формулой Грина [14]:

2 п^ ( r ) =

Тогда согласно формуле (6) на границе области сгоревшего газа «+»:

dr0 ∂r0 ∂r0           ∂r0

St = "at ^— VS = ^— h S) ^{— (} u n ^{+ V} ) dn =

∂r0

= — (uT ■ ik)  6an.

Рассмотрим также общее уравнение неразрывности:

∂ρ dt + u ■ Vp + p ■ div u = 0.(12)

Переходя в нём к переменным Лагранжа, находим [18]:

= I [г^Л        ⁺ ^ ⁽ r s ) ns '         ] ⁽ r s ) ■

I r s r I nss                             I r s r I

dp + ^ / ^{д ( u} x ,y^,z ) + ^{д ( x,u} y ^,z ) + ^{д ( x,}y^,u z ) A = o dtL ^p \ a ( x,y,z )      a ( x,y,z )      a ( x,y,z ) )      ,

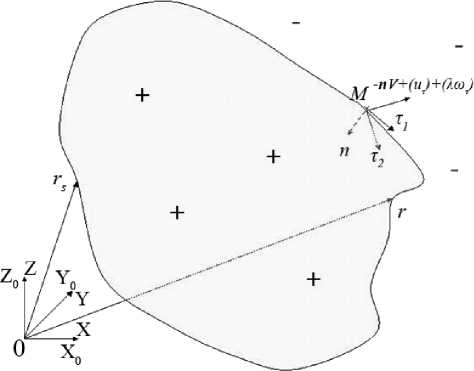
Рис. 1. Распространение фронта реакции в 3D-случае

^dP + P_ ■ ^{d Л} = o dt L Л dt L ,

то есть

∂r

P ^ ^Л = P ^ Ek, = P о ⁽ r о ) .

Тогда из уравнений гидродинамики (1)--(3) и условий сшивки (4)--(6) следует, что для любой точки на фронте

dt ⁺ u n - ⁺ 2 ⁽ u T ^— u П - ^{) +} P = o ,     ⁽⁸⁾

ш = —   - [ n X VP ] ,            (9)

θ где ω — завихренность сразу за фронтом реакции, и для простоты в данном разделе полная производная определена по формуле [15--17]:

d = _d_ _ V_d_ dt ∂t ∂n^.

Пусть для определённости выполняются общие уравнения гидродинамики и химической кинетики. Пламя будет тонкой областью, где физические величины претерпевают значительные изменения. Перейдём взаимно однозначно к лагранжевым переменным ( r о ,t ) (то есть к разметке):

Якобиан преобразования переменных (10) Л ~ 6 внутри фронта ограничен. Следовательно, в пределе 5 ^ 0, где 5 — толщина фронта, область пламени становится бесконечно тонкой и превращается в поверхность разрыва как в пространстве ( r,t ), так и пространстве переменных Лагранжа ( r о ,t ).

Завихренность (9), образующаяся за фронтом, зависит от кривизны фронта пламени и происходящих в нём внутренних процессов [2, 19]. Поэтому найти ее, не решая общих уравнений теории горения, крайне затруднительно. Однако можно в некотором смысле обойти эту проблему, направив время в обратную сторону. Мы знаем, что в 3D-случае уравнения Эйлера (1)--(3) допускают интегралы движения ш ■ Vr о = ш о ( r о ), см. приложение А. Тогда в системе координат ( п,т 1 ,т ₂ ), на границе области сгоревшего газа «+» должно выполняться соотношение

∂r 0       ∂r 0

ш 1--- + ш 2— = ш о ( r о ) ,

∂τ 1       ∂τ 2

так как из формулы (9) следует, что на фронте ш _п + = 0, см. [13]. Исключая дх о /дп , ду о /дп и ∂z 0 /∂n из уравнений (11) и (15), получаем

dx 0 dt

∂x 0 ∂τ 1 ∂x 0 ∂τ 2

dt

∂τ 1 ∂y 0 ∂τ 2

dz 0 dt

∂z 0 ∂τ 1 ∂z 0 ∂τ 2

+ 6 = 0 .

dr dt

= u ( r,t ) ,

r = r ( r о ,t ) , r о = r о ( r,t ) , r о | _t =o = r.

(1o)

Выразив из уравнения (16) r 0 через ω 1 , ω 2 , которые в свою очередь зависят от давления на фронте согласно формуле (9), и подставив результат в (17), чтобы найти P , получим в итоге замкнутую систему уравнений на поверхности фронта

для определения потенциала ϕ и скорости пламени V (уравнения (8), (9), (16) и (17)).

Физический смысл этой системы состоит в следующем. Пусть реакция (пламя) распространяется из некоторой точки зажигания. В некий момент времени «фотографируется» распределение завихренности за фронтом. Тогда с помощью уравнений (8), (9), (16), (17) можно описать всю эволюцию фронта реакции: от момента зажигания до момента фотографирования. В противном случае неизвестна была бы функция ш о ( r о ) на поверхности фронта, поскольку он, захватывая все новые и новые частицы, удалялся бы от области, где она определена. Если в некоторый момент времени мы имеем ш о ( r о ) = 0 во всей области сгоревшего газа, то из уравнения (16) следует, что ш ( r,t ) = 0 во все предыдущие моменты времени. Тогда скорость пламени V должна была бы определяться одновременно двумя разными условиями: с одной стороны, формулой Франкеля [10]:

V = 1 - (^Лт ⁽ n ^ >  f r—i^dS - ■ ⁽¹⁸⁾

а с другой стороны, системой уравнений (8), (9). Это невыполнимо, и, следовательно, завихренность всегда должна образовываться за фронтом, за исключением тривиального случая 9 = 1, что подтверждается прямыми численными экспериментами [6, 7, 20]. Этот простой пример показывает, что не все решения гидродинамических уравнений спереди и сзади фронта можно согласовать с условиями на границе, то есть не всякую задачу Коши можно здесь поставить.

Вместо перехода к переменным Лагранжа ( r о ,t ) (10), можно использовать более общее преобразование (A.5). Если же ш _п = 0, то принципиально ничего не изменится. Изменятся только формулы (11), где добавится слагаемое А • ш _т .

где r = r ( r о ,t ) и r о = r о ( r,t ), r о | t =о = r , а А ( r,t ) выбрано следующим образом:

ш ( r,t ) • VA ( r,t ) = 0              (23)

в области сгоревшего газа и

A ( r,t ) • ш п + = —9 — 5C

на границе сгоревшего газа. Из теории дифференциальных уравнений известно, что система (23), (24) имеет единственное решение. Из уравнения (24) всегда можно выразить A ( r,t ) на поверхности фронта реакции. В системе координат ( r о ,t ) граница прореагировавшего газа не движется. Действительно, пусть g о ( r о ,t ) = 0 — уравнение движения фронта реакции. Тогда скорость фронта равна

_{v =} _ g о t ₌ gt ^{+ (( и + Аш} ) • ^Vg )

V ^о+       IV о g о |               |V о g о |

= ^— |      , ^{( V +} u n + ^{+ Аш} п + ) = ⁰ .    ⁽²⁵⁾

IV о g о |

Аналогично уравнению (11), для точки M ( r,t ) на границе прореагировавшего газа имеем

dr 0 dt

^ — V^r ¹ + ( и т + Аш т ) •    = 0 , (26)

∂t ∂n              ∂τ

где d = d — Vd + (ит + Ашт) • d (27) dt ∂t ∂n              ∂τ

— полная производная по времени для движущейся точки M ( r,t ) [15-17]. В приложении A показано, что и в этих переменных интегралы ш•Vi о и А, где i = x, y, z , не зависят явно от времени, то есть А = 1, ш • Vi о = ш о i ( r о ), где ш _о ( r _о ) — распределение завихренности в начальный момент времени. Исключая ∂x 0 /∂n , ∂y 0 /∂n , ∂z 0 /∂n из формул

II.2. Фронт конечной толщины

Происходящие внутри пламени процессы можно учесть, вводя малые поправки в граничные условия на поверхности фронта [19]:

и + — и- = (9 — 1) n + 5A,(19)

P+ — P- = 1 — 9 + 5B,(20)

V = 9 — ип + + 5C,(21)

где A , B , C зависят от θ , u _- , P _- , кривизны фронта и внутренних параметров газа. В отличие от предыдущего случая здесь ш _п + = 5 [ V х A ] _п = 0 и порядка δ .

Рассмотрим точку M (r,t) на поверхности пламени, движущуюся со скоростью —nV + ит + Ашт (рис. 1). Перейдём взаимно однозначно в области сгоревшего газа к переменным начального положения частиц газа и времени (rо ,t) по формуле dr

— = и ( r,t )+ А ( r,t ) • ш ( r,t ) ,         (22)

dr о = д ( x о ,у о ,z о ) = 1 дт     д ( т 1 ,т 2 ,п )

ш п dr ! + ш 1 dr ! + ш 2 дт о = ш о ( r „ ) ,    (29)

∂n ∂τ 1      ∂τ 2

получаем выражение

ш п =

∂r 0

∂τ 1

∂r 0

∂τ 2

ш о ( r о )

К уравнениям (8), (9) в этом случае добавляются

поправки порядка δ/R :

-dt -^{+(1+ 5}C^—5A n ) ^и п - ^— 2 ^{( и} т ^{+ и}П, - ⁾⁺ P - = ⁰ , ⁽³¹⁾

ш + = — ^9—1 [ n X VP - ] + 5 Ф( A,B,C ) ,    (32)

θ где шп + = 5 [V х A] п.

Таким образом, система уравнений (26), (30)--(32) должна определять эволюцию фронта реакции. Ее преимущество состоит в том, что она реально описывает движение поверхности в терминах самой поверхности, а недостаток — что А ^ 1 /5 , то есть сильно зависит от конкретных свойств газовой смеси.

Предположим, что перед фронтом и за ним выполняется условие изоэнтропичности течения, а характерная скорость потока много меньше скорости звука. Тогда можно учесть сжимаемость газа, перейдя к новым переменным, при этом заменив уравнение (23) на

Хш .Vp + рш -VX = 0 .         (33)

В этом случае вместо интегралов движения ш -Vi о и Л следует использовать интегралы ш • Vi о /р и р Л (см. приложение A) и однозначную связь на поверхности фронта между давлением и плотностью P = P s ( р ), определяемую уравнением состояния. Если перед фронтом s = const, то эта зависимость сразу следует из уравнения состояния топлива. За искривленным фронтом происходит неравномерное нагревание продуктов горения, но выполняется соотношение s = P (1 — 1 /9 ) + const (это следует из второго начала термодинамики и закона Гесса). Если данное выражение для энтропии подставить в уравнение состояния прореагировавшего газа P = P + ( p,s ), то мы также получим однозначную связь между давлением и плотностью на границе пламени: P = P + ( р ), что и позволяет учесть образующиеся звуковые колебания. Выпишем уравнения для этого случая. C учётом изменения плотности формулы (28) и (29) примут вид

∂r0      ∂r0      ∂r0

ш дп + ш 1 8R+ ш 2 дТ2 = р^шо( rо)•

д(x о W о,z о) = р

д ( Т 1 ,т 2 ,п )      р о ( r о ) .

Интересно отметить, что, исключая ∂x 0 /∂n , ∂y 0 /∂n и ∂z 0 /∂n из формул (34) и (35), также получим уравнение (30). При этом отношение плотностей р/р о ( r о ) исчезнет. С условиями сшивки на фронте (19)--(21) надо теперь учитывать зависимость от температуры и плотности. Уравнения же движения фронта пламени остаются прежними: (26), (30)--(32). При этом незначительные звуковые изменения плотностей газа перед и за фронтом определяются по формулам P = P - s ( р ) и P = P + ( р ).

• I I.3. Влияние внешнего потока

Рассмотрим распространение бесконечно тонкого, слабо искривленного фронта реакции во внешнем вихревом течении газа (рис. 1). При этом рассмотрим точку M(x,y,z) на поверхности пламени, движущуюся со скоростью —nV + uT. Из уравнений Эйлера (1)-(3) в областях «—» и «+» и условий сшивки (4)--(6) для этой точки следует du 1 = d (u • тi) = dt dt

• =    ^^ (ш 2+ — ш 2 - ) — (1 — V) |V,(36)

du 2 = d ( U • Т 2 ) = dt dt

• =    9—1(ш 1 - — ш 1+) — (1 — V) £•

∂ω 1 -    ∂ω 2 -       ∂ω 1+ ∂ω 2+

• +    "эГГ = 9UTT + "327 )•

dшn   d (ш • n) = dt dt

• =    —ш п Г^ + 8 2 ) — 9 ( ⁸    +    ■■ ) . (39)

∂τ1   ∂τ2         ∂τ1

Формула (9) для давления на фронте при этом обобщается следующим образом:

9ш + — ш- = — (9 — 1)[n x VP].(40)

Предположим, что течение газа таково, что шп = 0. Чтобы замкнуть данную систему, необходимо ещё как минимум четыре независимых уравнения. Для этого перейдем взаимно однозначно в областях «–» и «+» соответственно к переменным начального положения частиц газа и времени (rо,t) по формулам dr = u(r,t)+ Х± (r,t) • ш(r,t),(41)

dt где r = r(rо ,t) и rо = rо (r,t), rо |t=о = r, а X± (r,t) выбрано следующим образом:

ш (r,t) -VX± (r,t) = 0(42)

в областях «—» и «+» соответственно,

X-(r,t) • шп = — 1(43)

на границе топлива и

X + (r,t) • шп = —9(44)

на границе сгоревшего газа. Из теории линейных дифференциальных уравнений в частных производных первого порядка известно, что система уравнений (41)--(44) имеет единственное решение. Из уравнений (42)-(44) можно определить Х± (r,t) и 8Х± (r,t)/дп на поверхности фронта реакции. Аналогично уравнению (25), в системе координат (41) границы исходного и прореагировавшего веществ неподвижны. Точке M(r,t) будут соответствовать две различные точки M- (r о - ,t) и M+ (rо+ ,t), движущиеся по внешней и внутренней стороне поверхности и совпадающие в начальный момент. Тогда из уравнений (41)--(44) их координаты описываются формулами dr о ± = dr о ± — y6r о ± + u ^ dr о ± =

• =    ^— ( ^Х ± ^ш т ± • -± ) .         ⁽⁴⁵⁾

Полную производную в уравнении (45) определим для простоты по формуле d = 8 — V-8- + ut • 8-.       (46)

dt ∂t ∂n ∂τ

Кроме того,

d / dr о ± \ _ d / dr о ± \ dt ∂n ∂t ∂n

V + ∂n ²

₊   • д / dr о ± \ _ / ди 1

^τ ∂τ ∂n       ∂τ 1

+

ди 2 ₊ ∂τ 2

∂λ ±

ω _n ∂n

■

∂ω 1 ± ∂τ 1

∂ω 2 ±

⁺ дт 2

∂r 0 ± ∂n

ω 2 ±

₊ ди п ± ∂τ 1

∂λ ±

ω 1 ± ∂n

_λ ∂ω 1 ± ∂r 0 ±

^± ∂n ∂τ 1

+ ( ш 1 ±

ди п ± + ∂τ 2

∂λ ±          ∂ω 2 ± ∂r 0 ±

⁺ Т П^{ш 2} ± ^{+ л} ± ^^Jl T T

А        д ² r о ± \

(^Л ± ^{Ш т} ± • дтдп ) .

(47) Аналогично предыдущему пункту, в переменных (41) интегралы ш • Vi о и Л не зависят явно от времени, то есть Л _ 1 и ш • Vi о _ ш о i ( r о ). В системе координат ( п,т 1 ,т 2 ) на границе пламени имеем

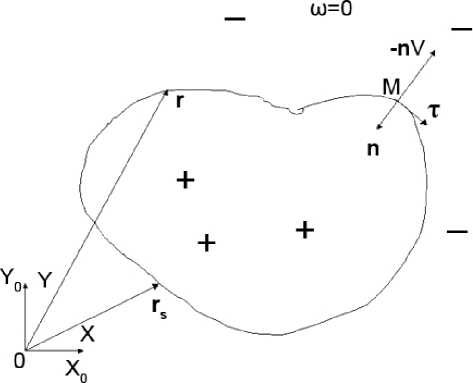
Рис. 2. Фронт реакции в 2D-случае

^{д (} x о ± ,y о ± ,z о ± )  1 д ( т 1 ,т 2 ,п )

∂r0±       ∂r0±       ∂r0± шп _х--+ ш 1 ± т:--+ ш 2 ± т:— _ ш о ±

∂n        ∂τ 1         ∂τ 2

( r о ± ) . (49)

В результате получим замкнутую систему (36)--(39), (45), (47)--(49) для определения V . Требование ш _п _ 0 здесь существенно. Последнее замечание предыдущего пункта относительно учёта влияния температуры и плотности остаётся в силе и здесь.

III. Неустойчивость Дарье–Ландау в 2D-потоке. Адиабатическое приближение

В этом разделе, не ограничивая общности, мы рассмотрим распространение двумерного (2D) бесконечно тонкого, слабо искривленного фронта экзотермической реакции (пламени) в потенциальном внешнем потоке (рис. 2). При этом течение газа вне фронта снова предполагается несжимаемым и невязким, но допускается неравномерное адиабатическое нагревание прореагировавшего вещества. Тогда гидродинамические уравнения принимают вид [2]

Граничные условия на поверхности фронта, следующие из законов сохранения, имеют вид (4)-(6) [11]. Скорости u n - _ дф/дп _ 1 — V и и _т _ дф/дт связаны между собой 2D-формулой Грина [14]:

ПФ(r,t) _ дф (rs,t)                           rs — r

_              ln \r s — r| — ф ( r s ,t ) n s  -------- dZ ( r s ) .

дn s                               |r s — r\ ²

Тогда из уравнений гидродинамики (50)--(53) и условий на фронте (4)--(6) следует, что для любой точки на поверхности фронта реакции