Нелинейное уравнение Шредингера в трех пространственных измерениях

Нелинейное уравнение Шредингера находит широкое применение в различных областях физики, например, в нелинейной оптике, физике плазмы, теории сверхпроводимости, физике низких температур. Для одного пространственного измерения теория нелинейного уравнения Шредингера детально разработана [1-3]. В этой статье рассматривается случай трехмерного пространства, т.е. изучается уравнение i дф/д t + V2v + 2рф|ф|2 = 0,                   (1)

где ф ( r , t ) - комплексная функция, n - вещественный параметр нелинейности.

Основной формализм

Найдем «стационарные» решения вида:

Ф(Г,t) = ф(г)eit,(2)

где е - свободный параметр. Подставляя (2) в (1), получим

V2ф-sф + 2пф|ф|2 = 0.(3)

Уравнение (3) допускает решения в классе вещественных функций, где оно принимает вид

V2ф = sф- 2рф3.(4)

Будем искать решение уравнения (4) в виде сложной функции ф = ф(и(r)), где и(r) = k(r-r0)/k . Здесь k - произвольная векторная постоянная k = (kx, ky, kz) , k = k^ + k^ + kz2 . Подстановка ф = ф(и(r)) в (4) даёт ф"(и) = Еф(и) - 2рф3 (и).                         (5)

Умножим последнее уравнение на ф' ( и ) и проинтегрируем. Получим ф' ² / 2 = V ( ф ) + C . Из граничных условий следует, что С =0. Интегрируя ещё раз, находим

J d ф /^2 V ( ф ) = и , или

J / d ^ф ₂ = ^{k ( r} — riV k .

ф7е-Пф

Вычисляя интеграл и обращая полученное выражение, имеем

, х        VETn

ф ^{( г )} = / г -----------\ .

ch I VE k ( r - r ₀)/ k I

Очевидно |ф| < ^ e / n . В силу симметрии (4) и (5) относительно преобразования ф ^ -ф , решением будет также ф a = -ф . Итак, окончательно

Ф ( г , t )

± 7 е / n e i ^{Е t} ch (V E k ( r - r ₀)/ k )

или, введя обозначение a = V e / n , откуда e = a ²n,

y ( r , t )

± a exp { ia ² n t } ch ( a Vn k ( r - r ₀) / k )

Если n < 0 , т.е. n = - |n|, то (5) принимает вид ф"(и) = Еф(и) + 2 |n| ф3(и), или ф"( и) = д V (ф) / дф,

Перепишем (5) в виде ф" ( и ) = д V ( ф )/ дф ,

где

V ( ф ) = ( ф ² +е /2 |n| ) ² |n| /2.

где V ( ф ) = ( е-пф ²) ф ²/2 . «Потенциал» V ( ф ) неотрицателен при |ф| < V е / n и имеет нули ф ₁ = 0, ф ₂ = V е / n , ф ₃ = -Уе / n , поэтому [4] граничными условиями для (4) примем ф ( г ) = ф i , i = 1, 2, 3 ; дф / д x i = 0 при | r |=w.

Так как дф / д x i = ф' ( и ) д и / д x i = ф' ( и ) k i / k = 0 при | r |=то, то это означает, что ф' ( и ) = 0 при | и |=».

Несингулярное решение последнего уравнения существует только при е< 0, т.е. е = -|е| , ф"( и) = 2 |п|ф3( и) -|е|ф( и).                            (6)

Интегрируя (6) тем же способом, что и (5), получим

± 1 f d ф

"^ ^Jф^{2 -}I^eI ^/2I ⁿ

= ^{k ( r} - ^r 0 )/ ^k .

Вычисляя интеграл и обращая полученное выра

жение, находим

ф ( г ) = ±

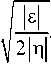
-^{k(r -} r > ^к ■

Согласно методу Коши [5], полный интеграл уравнения (10) имеет вид:

^{5 ( r )} = ^к у У 0 ⁺ k z z 0 ^{+ к} 0 ,

где к_у , k_z - произвольные постоянные, к ₀ - адди

Вводя обозначение VI^е! /2 HI = a , откуда е = - 2 a ² |n|, окончательно имеем

тивная произвольная постоянная, а у ₀ и z ₀ выражаются формулой (11), т.е.

ф ( r , t ) = ± a th I a ^Щ k ( r - r ₀) / k | exp { - i 2 a ² |n| t } .

5 ^{( r )} = k y

qy.         а ,

У--(x - x 0) + k qx

z ^- —⁽ x ^- x 0 ) q_x

⁺ k 0 .

В классе комплексных функций решение уравнения (3) ищем в виде

Ф ^{( г )} = ^{f ( r )} e q ,

где f ( r ) - вещественная функция, q = ( q x , q_y , q z )-свободный векторный параметр. Подставляя (7) в (3) и приравнивая к нулю мнимую и вещественную части полученного уравнения, находим

( q V f ) = 0,                                        (8)

V ² f = ( q ² +е ) f - 2 n f ³ .                       (9)

Уравнения (8) и (9) совместны, т.к. (8) является линейным однородным уравнением первого порядка и, как известно [5] из теории таких уравнений, решением уравнения (8) является любая дифференцируемая функция f = f ( 5 ( r ) ) , где 5 ( r ) - полный интеграл уравнения

( q V 5 ) = 0,

Аддитивную произвольную постоянную к0 выберем в виде k0 =-куУ0 - kzz0, тогда

5 ^{( r )} = k y

⁺ k z

или

д5 д5     д5 „ q + q + q = 0.

d x    y 5 y    5 z

Если одна из координатных осей, например ось х, является выделенной среди других, то выбираем переменную х в качестве параметра уравнений характеристик для (10), записав его в виде

д5 qy д5 q, д5 + у_+ дx qx ду qx дz

Уравнения характеристик

dx dy dz

¹     q y / q x    q z / q x

или dy = qy   dz = qz dx qx   dx qx элементарно интегрируются при начальных условиях У(x 0) = У 0, z(x 0) = z 0:

qy                   q

У = —^{( x - x} 0 ) ⁺ У 0 , ^z = — ^{( x - x} 0 ) ^{+ z} 0 . q_xq_x

Для нахождения полного интеграла выражаем отсюда начальные данные

У 0 = У ^- —^{( x - x} 0 ), ^z 0 = ^{z -} q ^^{( x - x} 0 )-      ⁽¹¹⁾

qxqx

qy

У - У0--(x - x0)

qx

^z - ^z 0 - qz- ^{( x} - ^x 0 ) q_x

+

В силу линейности уравнения (10) его полный интеграл можно умножить на любой числовой множитель 1/С, что сделано для дальнейшего удобства. Итак, ky (у - у0- (x - x0)qy / qx)

5 ( r ) = —-----------------^L +

C                         (12)

k_z ( ^{z - z} 0 ^{- ( x - x} 0 ) q z / q . )

.

C

Подставляя f = f ( 5 ( r ) ) в (9), получим

f "( 5 )

⁽ k y q y + k_zq_z ^{) 2} q x

+ k y ² + к²

= ⁽ q ² +e ) ^{f (} 5 ) ^- M ^{3 (} 5 ).

/ C ² =

Положим

^C = V^{( k} y q y ^{+ k} z q z ^{) 2 +} q x ^{( к} У ^{+ k} z ²) / q x .

Тогда (12) и (13) примут вид:

^к у [ q x ⁽ у ^- у 0 ) ^- q y ^{( x - x} 0 ) 1

5 ( r ) = ■                          = +

V^{( k} y q y ^{+ k} z q z ^{)2 +} q ^{2 ( к} У ^{+ k} _z ²)

+ ^k z [ q x ^{( z - z} 0 ) ^- q z ^{( x - x} 0 ) ]

V^{( k} y q y ^{+ k}_zq_z ^{)2 +} q x ^{( к} У ^{+ k} _z ²)

f Ч 5 ) = ( q ² +е ) f ( 5 ) - 2 n f ³ ( 5 ).                (15)

При п >  0 несингулярное решение уравнения

(15) существует только, если q ² + е = a ² . Тогда (15)

примет вид:

f "( 5 ) = a ² f ( 5 ) - 2 p f ³ ( 5 ),                       (16)

совпадающий по форме с уравнением (5). Повторяя ход решения уравнения (5), получим f (r) = ±1^L, ch a 5(r)

где 5 ( r ) выражается громоздкой формулой (14). Так

2    „2

как б = a - q , то окончательно

v ( r , t )

l a ^l^exp ( i t ^{qr + (} a^{2 - q 2)} t ] } . c as r

Если n< 0 , т.е. n = —|n| , то несингулярное решение уравнения (15) существует только при q ² + б = - a ² и (15) принимает вид:

f Ч 5 ) = ² |п| f ³⁽ 5 ) ^- a ² f ⁽ 5 )

совпадающий по форме с уравнением (6). Интегрируя (17) тем же способом, что и (6), находим х a , a 5 (r) f (r) = ± ,___th—

, 2Ini     v2

.

Учитывая, что б = - ( a ² + q ² ), окончательно имеем

a

V ( r , t ) = ± , th

a 5 ( r )

V2

{ i [ qr - ⁽ a ² + q ^{2 )} t ] } .

Нестационарные решения уравнения (1) будем искать в виде

v ( r , t ) = ф ( г , t )exp { i ( qr -ю t + Ф 0 ) } ,            (18)

где ф(г, t) - вещественная функция, q, ю и ф0 -свободные параметры. Подставляя (18) в (1) и приравнивая к нулю мнимую и вещественную части полученного уравнения, находим дф / д t + 2(qVф) = 0,                           (19)

V ² ф = ( q ² -ю ) ф- 2 рф ³ .                      (20)

Линейное однородное уравнение первого порядка (19) имеет своим решением любую дифференцируемую функцию ф = ф(5(r,t)), где 5(r,t)- полный интеграл уравнения д5 / д t + 2(qV 5) = 0, или в развёрнутой форме д5 J д5 д5 д5 ] .

— + 2 1 q x — + q y — + q z — I = 0 . д t ( д x д y д z J

Уравнения характеристик для (21) имеют вид dt dx dy dz

Т = 2q" 2q. " 2? ’ откуда dx

— = 2 q ,, dt ^x

dy        dz

— = 2 q y , т = 2 q z .

dt          dt

Эта система обыкновенных дифференциальных уравнений элементарно интегрируется при начальных условиях x (0) = x ₀, y (0) = y ₀, z (0) = z ₀:

x = 2 q x t + x 0 , y = 2 q y t + y ₀, z = 2 q z t + z ₀.

Выражаем отсюда начальные данные x0 = x - 2qxt, y0 = У - 2qyt, z0 = z - 2qzt.   (22)

Согласно методу Коши, полный интеграл уравнения (21) имеет вид:

• ⁵    = k x x 0 ^{+ к} у У 0 ^{+ k} z ^z 0 ⁺ k 0 ,

где k_x , k_y , k_z - произвольные постоянные, к ₀ - аддитивная произвольная постоянная, а x ₀, y ₀, z ₀ -выражены согласно (22), т.е.

• ⁵    = k x ^{( x - 2} q x t ) ⁺ k y ⁽ У ^{- 2} q y t ) ⁺ k_z ^{( z - 2} q z t ) ^{+ к} 0 -

• Аддитивную произвольную постоянную к0 выберем в виде

• ^к 0 =- ^k x ^x 0 ^- k y y 0 ^{- k} z ^z 0 ,

тогда

⁵ = ^k x ^{( x - x} 0 ^{- 2} q x t ) ^{+ k} y ⁽ y ^- y 0 ^{- 2} q y t ) ⁺

+kz(z - z0 - 2qztX что можно записать в векторной форме

5 = k ( r - r ₀ - 2 q t ).                               (23)

В силу линейности уравнения (21) его решение (23) можно умножить на любой числовой множитель 1/С, что сделано для дальнейшего удобства. Итак, окончательно

5(r, t) = k(r - r0 - 2qt)/ C .(24)

Подставляя ф = ф(5(r,t)), где 5(r, t) - определяется формулой (24) в (20), получим k1

ф"(5) C2 = (q2 -ю)ф(5) - 2рф3(5).(25)

Положим C = k = k x. + k y + k z² . Тогда (24) и (25) примут вид

5 (r, t) = k(r - r0 - 2qt)/ k ,(26)

Ф"(5) = (q2 - ю)ф(5) - 2рф3 (5).(27)

При n > 0 полагаем q ² -ю = a ² и (27) принимает вид:

Ф"(5) = a 2ф( 5) - 2рф3( 5 ), совпадающий с уравнением (16), и мы можем сразу записать его решение z х    ±a/Vn           ±a / vH

Ф ( г , t ) =---------= — ------------------ .

ch a 5 ( r , t ) ch [ a k ( r - r ₀ - 2 q t )/ k ]

Так как ю = q ² - a ² , то окончательно

± a exp { i T qr - ( q ² - a²)t + ф ₀ 1 }

V ( r , t ) =-----.

n ch [ a k ( r - r ₀ - 2 q t ) / k ]

Если принять здесь q = ( q , 0, 0), k =( k , 0, 0), то получим известное решение одномерного нелинейного уравнения Шредингера.

При п < 0, т.е. п = -|п| полагаем q ² -ю = - a ² и (27) принимает вид:

Ф"( 5 ) = 2 |п|ф ³ ( 5 ) - a² ф ( 5 )

совпадающий с уравнением (17). Следовательно, ± a    a

ф ( г , t ) =        th-j=s ( r , t ) =

V2H   ⁷²

= ± a th a ^k ( ^{r -} r o ^- 2 q t ) "

дЯП      2k^k

Учитывая, что ю = q ² + a ² , окончательно имеем

. .    ± a , a k ( r - r - 2 q t )

V ( r , t ) = ,--- th —-—-- — x

V2R      2kk     .

x exp { i [ qr - ( q ² + a ² ) t + ф ₀ ] }

Уравнение (30) является «двумерным» нелинейным уравнением Шредингера, в котором роль «времени» играет x I2 k₀ . Другими словами, (30) записано на < 3 , тогда как (1) на 1 ^3+/ .

Если искать решение в виде

E 0 ( r ) = f ( r ).,

где f ( r ) - вещественная функция, то подстановка (31) в (30) приводит к двум уравнениям:

В приведенных решениях амплитудные функции имеют вид гиперболических секанса и тангенса, аргументами которых являются линейные функции s( r ) или s( r ,t ). Для нахождения решений, зависящих от нелинейных функций s( r ) или s( r ,t ) нужно вместо полных интегралов линейных однородных уравнений первого порядка использовать особые интегралы.

Проиллюстрируем сказанное на примере решений вида (18), сводящихся к уравнениям (19) и (20). Найдем особый интеграл уравнения (19). Для этого исключим стандартным способом [5] произвольные постоянные k x , k y , k z из полного интеграла (26). Дифференцируя (26) по k x , k y , k z и приравнивая производные к нулю, найдем

, df    df    дf k0    + qy     ■ qz = 0 , дx    ду    дz

V , z f = (2 k 0 q x + q y + q z ) f - 2 p f ³ .

Уравнение (32) имеет своим решением любую дифференцируемую функцию f = f ( s ( r ) ) , где s ( r ) -полный или особый интеграл уравнения

ds qy ds qz ds --1----1--- dx k0 dу k0 dz

Полный s ( r ) и особый s ₀( r ) интегралы уравнения (34) найдены в [7]:

s ( r , t ) =

1 -----------------------------------------------7 (28)

= _х( x - x o ^{- 2} q x t ) + ⁽ y ^- y o - ² q_yt ) + ⁽ z ^- z o ^{- 2} q z t ) .

,, b y ^{[ k} 0 ⁽ у ^- у 0 ) ^- q y ^{( x - x} 0 ) 1

s (r) =    -------- y-------2 + k0 V by+ bz

₊ b z [ ^k 0 ⁽ z ^- z 0 ) ^- q z ⁽ x ^- x 0 ) ]

k 0 V b y + by        ’

Подставив ф = ф(s) в (20), получим ф"(s) + 2ф (s) = a2ф- 2рф3.                   (29)

s

Аналитические решения этого обыкновенного дифференциального уравнения автору неизвестны, однако легко найти приближенное решение при больших значениях s (что является оправданным в нелинейной оптике, где расстояния измеряются в единицах длин волн). Тогда вторым слагаемым в левой части (29) можно пренебречь и получим уже знакомое уравнение ф"(s) = a2ф(s) - 2рф3(s) ,

^s 0 ^{( r )}

'                         X2 /                        \2

q_y 1 1 q 1

^{y - y} 0 T" ^{( x - x} 0 ) I ⁺ l ^{z - z} 0 ^-_Л ^{( x - x} 0 ) I ,⁽³⁶⁾ k 0      JI      k 0      J

где x₀ , y₀ , z₀ - координаты центра пучка, b_y, b_z -произвольные постоянные. Подстановка f = f ( s ( r ) ) в (33) дает

^f "⁽ s ) = ( ² k 0 q x + q y + q z ) ^{f (} s ) ^{- 2} n ^{f 3 (} s ).

Вводя обозначение a = V2 k0 qx + qy + qz2,

имеющее решение

ф ( г , t )

a I УП ch as ( r , t )

последнее уравнение приводим к виду (16), имеющему решение

f ( r ) =

± a

П С ch as ( r )

где s ( r , t ) выражается формулой (28).

В стационарной теории оптической самофокусировки ключевую роль играет уравнение [ 6 ]

i 2 k 0 E + V yz E 0 + 2 _П| E 0^ E 0 = 0,           (30)

d x

где E ₀( r ) - комплексная огибающая электрического поля, k₀ — главная часть волнового вектора k = ( k 0 + q x , q y , q_z ), q x , q y , q z - малые поправки к

k ₀ = ( k ₀,0,0), n - коэффициент нелинейности среды.

Направим ось х через центр пучка. Тогда у₀ = z₀ = 0. С учетом (35) приходим к выводу, что вещественная огибающая (37) в любом сечении пучка x=const является гладкой ограниченной функцией, быстро стремящейся к нулю при удалении от оси х по всем направлениям, кроме прямой y = C j z + c ₂ , определяемой из уравнения s ( r ) =0, вдоль которой поле остается постоянным. В центральном сечении х=х₀ эта прямая имеет вид b_yy + b_zz = 0 . Таким образом, решение (37) описывает частично сфокусированный пучок.

Подстановка f = f (5o(r)) в (33) приводит к неавтономному уравнению f Ч 5 о) + f^0) = a2 f (50) - 2nf 450),         (38)

s ₀

имеющему при больших значениях s 0 (в единицах длин волн) асимптотическое решение

^f ( ⁵ 0 ⁽ r ) )

± a

П с ch a 5 ₀( r )

которое в любом сечении пучка x=const быстро стремится к нулю при удалении от оси х по всем направлениям, т.е. пучок является полностью сфокусированным. Однако, поскольку (39) является асимптотическим решением, остается открытым вопрос о поведении функции (39) вблизи центра пучка. Точное решение уравнения (38) не должно иметь сингулярностей, чтобы быть физически допустимым решением.

Для численного решения, уравнение (38) с по- a мощью преобразования ^ = a50, f = —j=u приво-V n дим к безразмерному виду u"© + uy) = u© -2u3©.              (40)

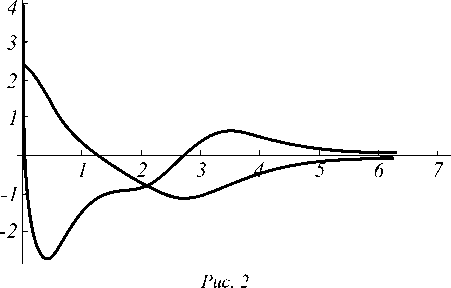
На рис. 1 и 2 представлены численные решения уравнения (40) и их производные. Выходящие из начала координат кривые – графики производных u ' ( ^ ) соответствующих решений u ( ^ ).

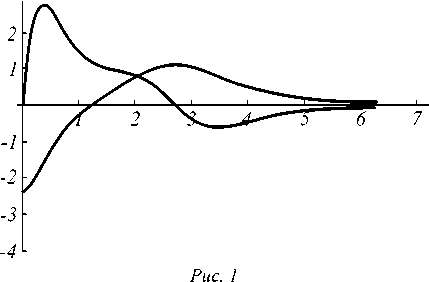
Из графиков следует, что решения уравнения (40) являются гладкими ограниченными функциями, асимптотически стремящимися к нулю, а также, что уравнение (40) обладает симметрией относительно преобразования u ^ -u .

Работа выполнена при поддержке Министерства образования и науки РФ, правительства Самарской области и Американского фонда гражданских исследований и развития (CRDF Project SA-014-02) в рамках российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE, REC N 14).

Заключение

Найдены в аналитической форме гладкие решения нелинейного уравнения Шредингера в виде уединенных волн для случая трех пространственных измерений. Рассмотрено явление оптической самофокусировки.