Нелинейное усиление оптических сигналов в периодически неоднородном двухмодовом световоде

НЕЛИНЕЙНОЕ УСИЛЕНИЕ ОПТИЧЕСКИХ СИГНАЛОВ

В ПЕРИОДИЧЕСКИ НЕОДНОРОДНОМ ДВУХМОДОВОМ СВЕТОВОДЕ

Как известно, последние поколения ЭВМ практически исчерпали физические возможности электроники по увеличению быстродействия. Дальнейший прогресс в этом направлении может быть достигнут переходом к оптическим скоростям передачи информации. Соответствующие длительности сигналов должны составлять единицы пс. Формирование таких импульсов и их транспортировка по одномодовым оптическим волокнам надежно освоена в последние годы. Однако для создания элементов ’’оптической логики” сформированные импульсы нужно уметь усиливать и переключать. В настоящее время в этом направлении ведутся интенсивные поиски. В частности, можно выделить ряд схем, реализующих нелинейное взаимодействие двух одномодовых импульсов в сона-прав ленных световодах [1-8]. При этом максимумы поперечных распределений мод удалены друг от друга, что снижает эффективность взаимодействия. Дальнейшее улучшение энергетических характеристик можно искать на пути объединения двухмодовых импульсов в одной сердцевине световода. Такая попытка и предпринята в настоящей работе. При этом мы ограничимся рассмотрением стационарного случая, полагая, что длины нелинейного взаимодействия гораздо меньше длин дисперсионного расплывания. Однако в отсутствии дополнительных возмущающих факторов нелинейность, влияя на фазы мод, не в состоянии изменить их амплитуды. Роль требуемых возмущений, как показано ниже, с успехом может сыграть периодическая по длине неоднородность, период которой согласован с разностью волновых векторов мод.

Общая теория нелинейного взаимодействия коротких многомодовых импульсов в возмущенной среде подробно разработана в [9]. Ниже соотношения [9] конкретизируются в рамках следующих предположений:

• 1)    опущены все нестационарные составляющие (связанные как с дисперсией, так и с инерцией нелинейности) ;

• 2)    не учитывается влияние поглощения;

• 3)    не учитываются характерные для тонких волноводов эффекты, пропорциональные (Х/а)^, где X - длина волны, а — поперечный масштаб (здесь следует отметить, что в уравнениях эволюции для ТЕ - распределений поля подобные слагаемые автоматически исчезают независимо от величины Х/а);

• 4)    высота поперечного профиля показателя преломления п(г) предполагается малой (модель слабонаправляющего волновода). При этом в амплитудах всех функций (но не в фазах!) пренебрегается различием волновых векторов k_m, т. е. полагается k] = к₂ = ш ■ n/с, где со — частота волны;

• 5)    игнорируется влияние слагаемых, не удовлетворяющих фазовому синхронизму.

Пусть в световоде с продольной осью z распространяется двухмодовый волновой пакет (рис. 1), электрическое поле которого записывается в виде:

^ = Re [£0 „^г^^^т!^) exp(ikmz-iwt)],                               (1)

где fm (г) - безразмерные комплексные амплитуды; е"т^ - нормированные модовые векторы поперечных рас-пределений: < I ет^ г>=1 (для осесимметричной структуры волновода <А> = / 2nRdR ■ A, R = r/а, а — ради-

Рис. 1. Схема ввода-вывода мод:

f J - сигнальная мода; f2 - мода накачки; М - моданы, формирующие двухмодовую структуру на входе или разделяющие моды на выходе ус световода). Тогда в рамках указанных допущений уравнения эволюции модовых амплитуд f примут согласно [9] вид:

^dfm _ ^неод ₊ RHen                                                                           (2)

dz ™          ’ где Rm описывают влияние неоднородности и нелинейности.

Для периодической неоднородности при 6 п^неод = 8п “^е_а°^д (г) • cos (qz + ф_г) в рамках фазового синхронизма с волновыми векторами мод (q = kj — k₂) из [9] получим:

Кнеод= ь r.f2 кнеод= j.r*.fp

Г = ^ • < (=11 ‘ «21) " 6nm °х”> ' ехР О^                                                  <3>

Существует несколько традиционных механизмов реализации периодической неоднородности, например — гофрировка волновода, возбуждение продольной ультразвуковой структуры и др. [10]. Мы конкретизируем случай гофрированного световода, в котором радиус сердцевины меняется по закону a (z) = а + 6 а ■ cos (qz + ф ). полн                            г

Далее будем рассматривать простейший параболический профиль (рис. 2) n = n. [ 1 - △ • r²/a² (z)] , где Д = (п -ⁿd^ⁿc "^ ¹ ~ высота профиля, а п_с и n_d соответствуют сердцевине и оболочке световода. Тогда 8п^нсод = = 2 • п Д R² 5 а/а. Используя азимутальные ТЕ₀₁ и ТЕ₀₂-моды Лагерра [11, 12]:

е,=~^ exp(-vR2/2), е2 =-^ . (2 - v - R2) - exp (-vR2/2), k^ =-^ n2--4^- ' т-

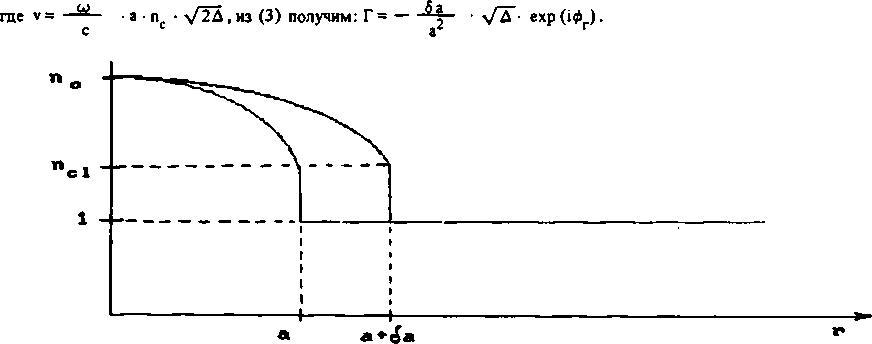
Рис. 2. Профили п (г) для гофрированного световода

Конкретизируя влияние нелинейности, следует, вообще говоря, обратить внимание на зависимость структуры нелинейного отклика 8пнел на основной частоте от механизма нелинейности. Например, сила Лоренца в плазме инициирует в направлении исходного поля Е? генерацию третьей гармоники. При этом, как нетрудно показать, 6пнел пропорционально Igrad ^ Р. Для многих простейших безынерционных механизмов нелинейности характерным является отклик 5пиел = (^ • ^). Используется также и пропорциональность 6пнел интенсивности сигнала, т. е. вектору Пойнтинга I = 1^ х Z lz [ 13]. Различия феноменологической структуры нелинейного отклика приводят к различию результатов его влияния, что особенно проявляется в тонких волноводах при наличии в модах продольной компоненты Ег Строгая эквивалентность указанных типов отклика 8пнел достигается лишь для плоских волн, либо в одномодовом ТЕ-распределении. Приближенная эквивалентность реализуется, как нетрудно показать, при выполнении упоминавшихся выше условий 3) и 4). Таким образом, далее будем считать 6пнсл = = п2 ■ I « с • е0 • n • i^ • (5-^) ([^J =м2/Вт),что для вектора нелинейной поляризации^*сл означает при указанных допущениях зависимости ?*сл = 2 - е^ • с • п2 • п2 •         - . Тогда, согласно [9], для Б^л в рамках фазового синхронизма получим:

R?e” = i-А (иц If,!2 +u12-If^M,,

R"2e”=i A (u21lf1l2 ♦u22.|f2P).f2,                                                        (4)

to • n2 ■ Q                3      -»   4

A ⁼ ------T -- 1          ⁼ --- ' < I I > .

c-a2-|fO|2 mm 2 ml                                                       (4)

u,₂= «21 =< till² Al*² + 2.(^₁?₂₁i²>.

oo

При этом Q = / 2nrdr • Iq ([Q] = Вт) — интегральная мощность нормирующей моды на входе в световод (далее — это мощность накачки (2-я мода)), | (^| - соответствующая этой моде входная амплитуда: f_kl_z=0 = 11^1 ^х х exp (i0_k) (Ф_к -начальные фазы). Вводя теперь характерную нелинейную длину L^HCn, так что 1/Ь^нел = А ■ Пц, для азимутальных TE_Q1 и TE_Q2 Лагерровых мод получим:

1/Ькел =

Va- П₂ Q/!^I²           2яс

—----------,где X °*--длина волны.

2 • n • a • X2                  tonc

При этом u12 = Uu, u22 = -y • un.

Таким образом, комбинированное нелинейно-неоднородное взаимодействие двух мод описывается системой уравнений:

dz

^ (Ки If,!2 * R12- If,!2)-^* 1 Г-Г2.

^2 dz

— •(R21lf1l2*R22lf2l2)f2*ir*.f1,

U12          U22

где R_u - 1, R₁₂ - R₂i - u^'R^”     ¹

Как нетрудно показать, энергетический интеграл системы (5) сохраняется при любом наборе параметров: W( + + W2 = const (z), где Wm = lfm ?.

В отсутствие нелинейности (1нел •♦ *) система (5) описывает обычный гармонический режим перекачки энергии из одной моды в другую. А именно:

W] = —^----2°- + р • cos (2 1ГI z t а), cos а = —ш^,

1    2>—21----------------------------------- <

В отсутствие неоднородности меняются, как нетрудно показать из (5), лишь фазы мод: Wm =*т0. Фт = = Ф° +(Rml w._ + Rm, w2n).z/LHen. m v ml 10 m2 2071

В общем случае решение системы (5) также доводится до квадратуры:

(^-)2 = 4- irl2 w, (w10 +w20-w1)-(a w2+в-w,+с)2, 1

А- 2 (R12 + R21  R11

В= (R22 * R1 2) ' ^10^20)'

C= 2- lrl.VW10 W20 cos(0°-^-«r) -A W20- В W10.

Отсюда, в частности, видно, что эволюция модовых амплитуд зависит от начального сдвига фаз ДФ₀⁼ (Ф® - Ф₂ ~ - Ф_г), если на входе присутствуют оба сигнала: W_]Q • W_2Q ^ 0. Эту зависимость при необходимости можно ослабить, оптимизируя параметры R_mn, W_mo, ITl, что, однако, выходит за рамки настоящей работы. Кроме того, из (7) ясен периодический характер эволюции амплитуд, описываемый эллиптическими функциями.

Исследуя свойства системы (5), либо квадратуры (7), нетрудно обнаружить ее усилительные возможности. Действительно, пусть на входе в световод (z = 0) задана 2-я мода (накачка), но отсутствует 1 -я (сигнал): WjQ = 0, W2Q = 1. При этом амплитуда 1-й моды будет осциллировать с некоторым периодом zQ. Если же на входе вместе с накачкой присутствует слабый сигнал (например: W]0 = 0,1, W2Q = 1), то период пульсаций изменится. Наложение соответствующих кривых наглядно демонстрируется на рис. 3. При этом в точках, кратных 50 = z0/LHen, отсутствие входного сигнала приводит к обнулению, а присутствие малого W10 * 0 - к достаточно большим величинам W1 'f=kf0- Аналогичные кривые были просчитаны для различных масштабов неоднородности (рис. 4). При этом в случае Дф0 = 0 найдено оптимальное для усиления сигнальной моды значение: Г • Ьнел =0,11.

Помимо описанных усилительных свойств рассматриваемая система (5) позволяет также осуществить своеоб разный перевод фазовой модуляции сигнала в амплитудную. Действительно, если разные части входного сигнала

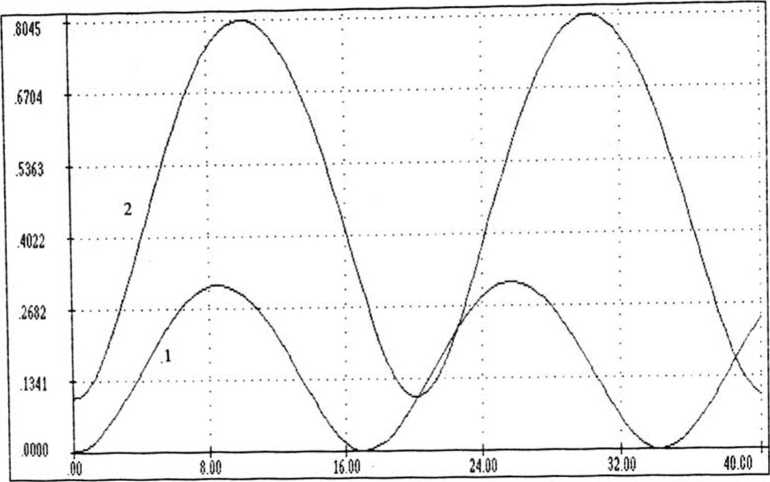
Рис. 3. Распределение энергии сигнальной моды по длине световода для Г- L^Hcn = 0,11: 1 - в отсутствие сигнала на входе 0V| q ⁼ 0); 2 - при наличии Wjq =0,1 и Д^д =0

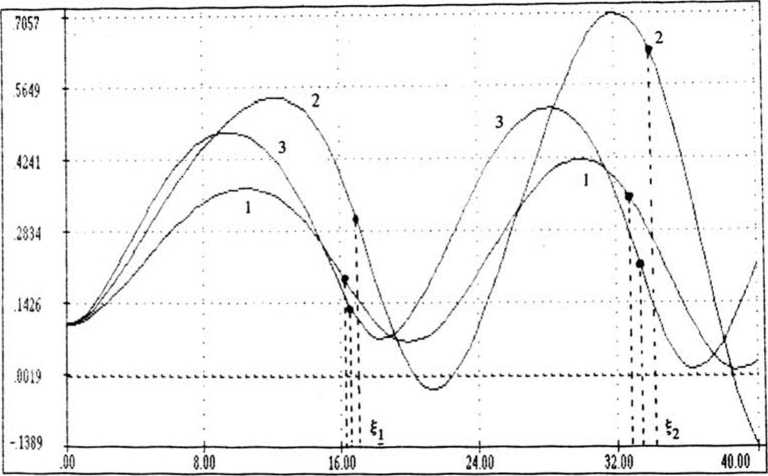
Рис. 4. ДW1 - разность кривых 2 и 1 из рис. 3 при Wj Q = 0,1, Д Фо = 0 для:

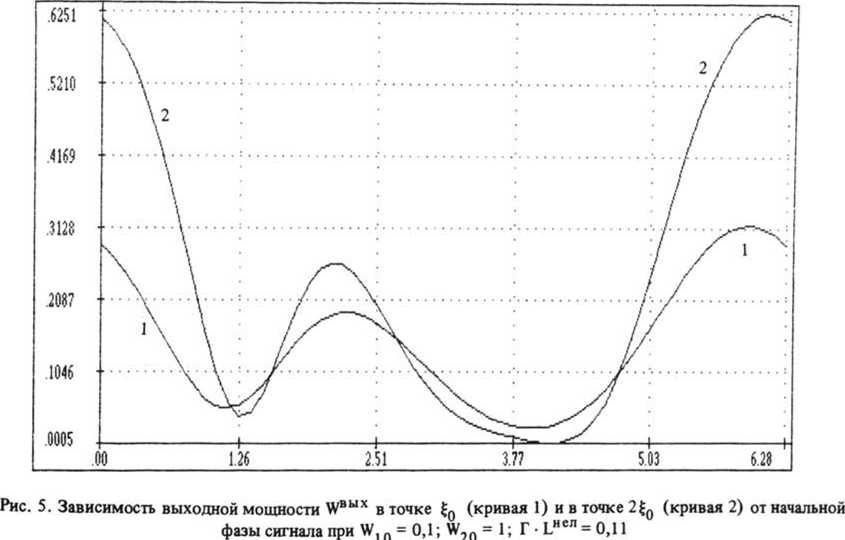
1 - Г • LHC" =0,07; 2 —Г LHcn=0,ll (оптимальное); 3 - Г • LHen =0,15. В точках ^д достигается максимальный контраст, равный единице имеют различную фазу, то соответствующие им части выходного импульса будут преобразовываться по-разному. Если расположить выходное сечение в точках максимального контраста ^0 и 2$0 (см. рис. 3), то зависимость выходного W] от начальной фазы сигнала дается кривыми, изображенными на рис. 5.

Следует отметить структурное сходство системы (5) с уравнениями туннельной связи идентичных мод в разных сердцевинах световода [7]. Для формального перехода достаточно упростить (5), вычеркнув нелинейные перекрестные слагаемые (пропорциональные R^ и R21) или соответствующим образом преобразовав переменные.

Отсюда ясно, что все физические свойства, присущие нелинейной туннельной связи, автоматически переносятся на случай нелинейного взаимодействия мод в периодически неоднородном световоде.

В заключение можно привести оценочные значения параметров, формирующие LHen для кварцевого световода: п =“ 1,4 ; а =“ 2 мкм; Д ^ 0,04; X ^ 0,5 мкм; п2 ^ 4 • 10-20 м2/Вт; Q “ 1 Вт. Тогда Ьнсл “ 13 м. Таким образом, расстояние до первого максимального контраста составляет 100-200 м, что при использовании импульсов * 10 пс позволяет игнорировать дисперсионное расплывание, длина которого в этих условиях =1 км.