Нелинейное возбуждение квантового резонанса Фано

Для описания автоионизационных состояний атомов имеется надежная теория, позволившая, в частности, понять динамику ионизации таких состояний аттосекундными импульсами [1-7]. Основными результатами усилий в этом направлении стало понимание внутриатомной составляющей динамики, отвечающей за. формирование зависящего от времени дипольного отклика. [8,9] и динамики образования электронов в непрерывном спектре [10], убедительно подтвержденные экспериментальными измерениями. При образовании электронов непрерывного спектра, важной оказывается конкуренция процессов прямой ионизации и ионизации, идущей через возбуждение дискретного состояния, меняющаяся во времени. Большая часть имеющихся теоретических исследований посвящена, изолированным резонансам, но рассмотрено и влияние перекрытия резонансов на. их динамику [11]. Отметим, что для квантовых точек возбуждение экситонов находится в видимой области света, где изучение резонансов Фано облегчается наличием развитой экспериментальной техники получения одноцикловых лазерных импульсов [12,13].

Все эти теоретические и экспериментальные усилия объединяет квантовая интерференция, которая проявляется как резонанс в спектре оптического поглощения с характерной асимметричной формой. Близко к основному максимуму возникает глубокий минимум

при энергии, соответствующей деструктивной интерференции амплитуд перехода в дискретное состояние и непрерывный спектр состояний. Важной основой теории Фано является предположение о достаточно высокой плотности состояний, которые можно отнести к непрерывному спектру. Однако в ряде случаев множество близко расположенных уровней оказывается достаточно разреженным. Такая ситуация присутствует в молекулярных спектрах многоатомных молекул, где электронные переходы релаксируют, взаимодействуя с колебательными молекулярными состояниями. Этот случай в отсутствие прямого возбуждения уровней зоны проанализирован в модели Биксона-Джортнера [14]. Настоящая работа посвящена исследованию динамики резонансного возбуждения состояния на фоне зоны эквидистантных уровней лазерным полем в модели Биксона-Джортнера, дополненной с возможностью прямого оптического перехода в зону уровней.

2.    Общие уравнения динамики

Рассмотрим квантовую систему, состоящую из основного состояния |0) и возбужденного состояния |1) с энергией Ei, взаимодействующего с зоной близко расположенных по энергии уровней |k) с энергиями Ek- В данной модели возможно прямое возбуждение лазерным полем дискретного уровня и уровней зоны, как показано на рис. 1.

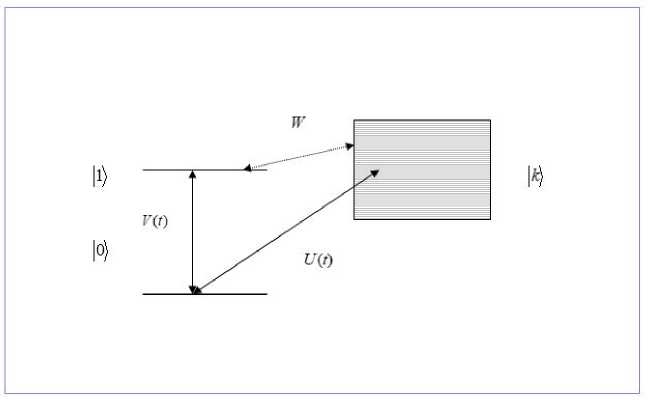
Рис. 1. Схема, возбуждения двухуровневой системы, взаимодействующей с зоной уровней

Пусть гамильтониан системы Н является суммой гамильтониана Но, представляющего независимые состояния, стационарного взаимодействия Wвoзбyждeннoго состояния |1) с уровнями зоны Д) и внешнего зависящего от времени взаимодействия Hint(t) = И(t) + U (t). Взаимодействие И (t) связывает осповнос состояние |0) и возбужденное состояние |1). U (t) связывает основное состояние |0) и возбужденные состояния зоны Д):

Н = Но + W + И (t) + U (t).(1)

Уравнение Шредингера. гф = Нф(2)

в представлении взаимодействия принимает вид га о = Ду-Й + ^иок(1)еІШ№ tak, iai = Цо(Щ'"-Мо + £Wik e'"« ^k,(3)

к гак = Uko^ao + Wkie^ai.

Аналитическое решение системы уравнений (3) возможно в случае резонанса.

Величины qq , 01 , Ок являются коэффициентами разложения волновой функции

W) = 52е tEjаз(^^з + 52 е гЕ"о™^)^(4)

1=0,1п по собственным состояниям <рк оператора Гамильтона Hq, удовлетворяющим уравнению

Но-Л = Ек ук,(5)

И шкк1 = Ек - Ек1.( 6 )

Начальные условия    для первоначально невозбужденной системы:

qq(0) = 1 ,о1 (0) = 0, Ок(0) = 0. При дополнительных предположениях W^ = W _{1 k} = W,

• VQ1(t) = V]_o(t) = U1(t), U^ = U^_k = U ₂ (t) систему уравнений (3) можно упростить, и мы получим

го q = Ui(t)e^^01toi + U2(t) ^ е^іш0^к^к,

к го 1 = UJПе'-' "Щ,, + W ^ еІШ1к^к,                             (7)

к гОк = U2(t)eiUkotOQ + We^k1 toi.

Далее рассматриваем возбуждение системы лазерным полем с мгновенным включением и постоянной фиксированной несущей частотой. Взаимодействие носит квазирезонансный характер, поэтому, удерживая только резонансные слагаемые, в приближении вращающегося поля получим систему уравнений:

гоq = Vie-i(ui0-u)toi + V2 ^ е-i(шk0-ш)tОk, к го 1 = V1еi(ш10-ш)tОQ + W ^ еІШ1к tОk,                                (8)

к гак = V2el(uk0-u)toQ + WelUk1to1.

Вводя новые амплитуды в соответствии с определениями:

Ок = е^і(шк0-ш^Ак , о1 = е^^10-^^,                               (9)

qq = А0, получим уравнения [15,16]

гАо = V1A1 + V2 ^ Ак, к гА 1 = Д1А1 + ViAq + W ^ Ак,                     (Ю)

к гУ^к = Ак Ак + V2Aq + WA1, где А1 = W10-ш-г^, Ак = Шко-ш-г^к, коэффициенты у, ^к позволяют феноменологически учесть затухание возбужденных уровней. В области изображений преобразования Лапласа система уравнений (10) принимает вид saq = -гV1A1 - гГ2   Ак + 1,

к sAx = -гА1А1 - гV1AQ - гW ^Ак,                    <и)

к sAk = -гАкАк - гV2AQ - гWA1.

Из последнего уравнения следует

и

^A k =

. V>Aq + W Ai г---;--------:—:---

(s + гАк)

sAq = -гV1A1 - ( V ^ A q + V2WA1) V . , \ . +1, V ^{(s + гА}к)

sAi = -гАiAi - гУі Ao - (V₂WAq + W 2A1) V ,  , \ A .

^{(s + гА}к)

После вычисления суммві в правой части уравнений (13), приведенного в [17], получим

V 7   ~ coth Д),

“ (s + гАк)    wq V^o/

где расстояние между эквидистантными уровнями зоны равно wq. Для плотного спектра (квазиконтинуума) ts/wq >> 1 и coth(^s/wo) ~ 1, тогда будем иметь

sAq = -iVAi - (y,2Ao + V2WA1) — + 1, wq sAi = -гАiAi - гV1Ao - (V2WA0 + W2A1) —. Wo

Для удобства дальнейших преобразований введем обозначения:

V2 т      ^V₂W       ^w ²

wq =---, w_c =-----, w =----

Wq           Wq           Wq

.

С учетом этого решение системы уравнений запишем в виде

Aq(s) =

s + гАі + w

(s + wq)(s + гАі + w) - (гУі + w_c)² ' гУ1 + w_c

A1(s) =--2,

( s + wo)(s + гА1 + w) - (гУі + w_c)²

A (s) = г_______W(гУі +wc) - V2(s + гАі + w)_______ k       (s + гАк)[(s + wq)(s + гАі + w) - (гУі + wc)2]

Выражения (17) переходят в решения [16], полученные с помощью преобразования Фурье, при замене s ^ -гw. С течением времени в непрерывном спектре формируется квазиста-ционарное распределение:

Ak (t) = г

у ₂ (а _і - Ак - гw) - w (V - гw_c) (Ак + гwo)(Аi - Ак - гw) + (Уі - гw_c)²

exp(-гАк t).

Выражение (18) имеет два полюса, что приводит к двугорбой форме заселенности уровней, характерной для интерференционного профиля Фано.

3.    Квантовый резонанс на фоне дискретного квазиконтинуума

Рассмотрим пример зависимости заселенности уровней зоны от энергии при точном резонансе, когда Аі = 0. На рис. 2 показано конечное распределение заселенности зоны уровней Рр_апо(А_к ) = |A_k(t)|² при параметрах: w₀ = 0.0011 эВ. W = 0.001 эВ. V1 = 0.0022 эВ. V = 0.0018 эВ, у = 7к = 0. Отметим, что асимметричная форма распределения нелинейным образом зависит от величины поля и может существенно отличаться по виду при других значениях параметров.

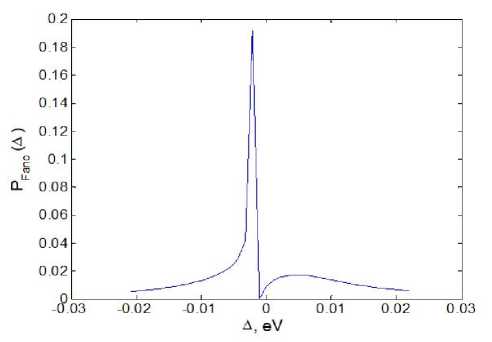
Рис. 2. Финальная заселенность квазиконтинуума в форме Фано

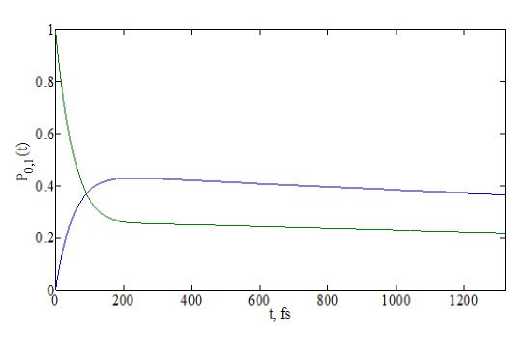
Рис. 3. Динамика заселенности уровней |0) и |1)

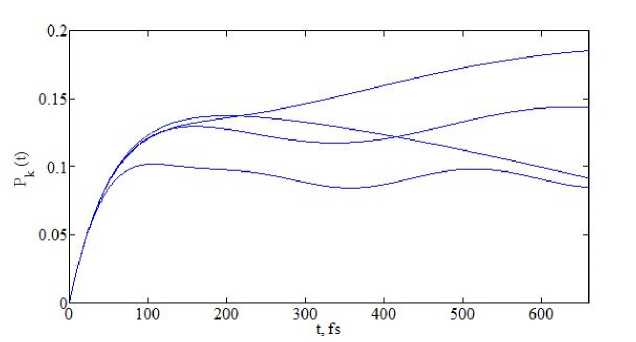
Рис. 4. Динамика, заселенности уровней квазиконтинуума с энергиями -0.015 эВ; -0.005 эВ; 0 эВ;

0.01 эВ, отсчитываемыми от резонанса: начальный период времени

На рис. 3 представлена, временная зависимость заселенности основного и возбужденного резонирующих уровней. Вначале их заселенности принимают сопоставимые значения за. счет резонансного воздействия поля. Далее заселенности монотонно снижаются за счет распада, в квазиконтинуум.

На рис. 4, 5 показаны результаты расчета, динамики заселенности четырех выделенных состояний квазиконтинуума. Рис. 4 более подробно показывает начальный период возбуждения квазиконтинуума, стартующий с нулевых заселенностей. Рис. 5 отражает глобальную динамику заселения квазиконтинуума, носящую характер затухающих осцилляций вокруг асимптотического значения заселенности. Финальные заселенности уровней соответствуют значениям, представленным на рис. 2.

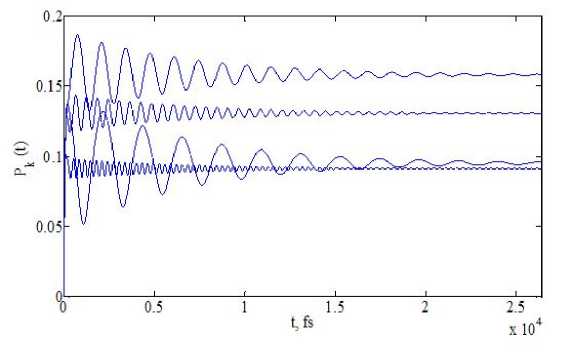
Рис. 5. Динамика, заселенности уровней квазиконтинуума с энергиями -0.015 эВ; -0.005 эВ; 0 эВ;

0.01 эВ, отсчитываемыми от резонанса: глобальная динамика.

Отметим принципиальное отличие полученного асимметричного распределения от линейного профиля Фано. В случае линейного резонанса. Фано интерференционный провал образуется при определенных значениях сканирующей частоты. В нелинейном резонансе частота, внешнего поля фиксирована, а. асимметрия распределения заселенности квазиконтинуума обусловлена, совместным действием нелинейности и интерференции.

4.    Заключение

Проведенное исследование показывает важность интерференции каналов при нелинейном резонансном возбуждения дискретного уровня на. фоне плотной зоны уровней. Отмечается возможность формирования асимметричного профиля за. счет интерференции, характерной для резонансов Фано. Приведено динамическое описание формирования резонанса, показывающее возможность управления формой заселенности квазиконтинуума в широких пределах за. счет изменения отстройки частоты внешнего поля и его интенсивности. Важно отметить, что оптически перестраиваемый резонанс на фоне континуума является, в частности, моделью системы, состоящей из нанопроводника, и примесных атомов, обеспечивающих дискретные состояния на. фоне континуума. [18]. Это позволяет провести экспериментальное исследование нелинейной динамики резонанса. Фано, используя лазерное поле оптического диапазона. Проведенное нами исследование существенно опиралось на. монохроматичность и квазирезонансность внешнего воздействия. В то же время наибольший интерес представляет изучение динамики наносистем под действием фемтосекундных импульсов. Для столь коротких лазерных импульсов резонансное приближение становится слишком грубым, и требуется использовать иные теоретические схемы анализа, включая прямое численное моделирование динамики.

Работа, выполнена, в рамках Государственного задания Министерства, науки и образования РФ (задание № 3.9890.2017/8.9).