Нелинейность силы межатомного взаимодействия и упругие свойства твердых тел

В уравнение состояния твердого тела входит параметр Грюнайзена у , характеризующий нелинейность силы межатомного взаимодействия и ангармонизм колебаний решетки. Основным соотношением для экспериментального определения у является уравнение (закон, формула) Грюнайзена [1]

β VB

Y = ^,

^C V                                    (1)

ВЕСТНИК БУРЯТСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА.

где р — коэффициент объемного теплового расширения, V — молярный объем, B — изотермический модуль объемного сжатия, C V — молярная теплоемкость при постоянном объеме.

Помимо этого уравнения для расчета у используются другие выражения, в том

числе формулы Леонтьева [2]

Y =

3 f BA- 1

2 I Р v K J

и Беломестных–Теслевой [3]

Y = ~

1 + И 1

2 - 3ц )

Здесь B A — адиабатический модуль объемного сжатия, р — плотность, v _K — средняя квадратичная скорость волн деформации, квадрат которой является инвариантом суммы квадратов скоростей распространения продольной ( v L ) и поперечной ( v_S ) упругих волн

v

к

v 2 + 2 vs2

ц — коэффициент Пуассона, который иногда называют коэффициентом поперечной деформации. Формулы Леонтьева (2) и Беломестных–Теслевой (3) привлекательны тем, что в отличие от уравнения Грюнайзена (1) позволяют рассчитывать у по более доступным экспериментальным данным. Установлено, что они находятся в удовлетворительном согласии с уравнением Грюнайзена [3-5] (например, рис. 1).

Вместе с тем обращает внимание то обстоятельство, что в формулах (2) и (3) в левых частях равенств находится мера ангармонизма у , а в правые части входят на первый взгляд только гармонические характеристики ( р , B A , v²_к) и ц . Тем самым наблюдается как бы противоречие.

В настоящем сообщении развито представление о том, что правые части равенств (2) и (3), зависят от ангармонизма (неявно) через зависимость отношения квадратов скоростей звука (ν² L /ν² S ) от параметра Грюнайзена γ и поэтому указанное выше противоречие на самом деле является кажущимся противоречием.

Линейная зависимость ( v l² / v s² ) от параметра Грюнайзена

При изучении формул (2) и (3) обнаруживается тот факт, что их правые части являются функциями отношения квадратов скоростей распространения продольной и поперечной акустических волн (ν² L /ν² S ). Так, например, в уравнении Леонтьева (2) за счет величины ν² к правая часть равенства оказывается функцией указанного отношения ( v _L/ v _S)² (соотношение (4))

Рис. 1. Линейная корреляция между значениями параметра Грюнайзена у , полученными по уравнению Грюнайзена у (1) и по формуле Беломестных-Теслевой у (3), для различных кристаллов (использованы данные [3, 4]).

1 — Be, 2 — LiF, 3 — NaCl, 4 — LiCl, 5 — KCl, 6 — KBr, 7 — Al, 8 — Ag, 9 — Pb, 10 — Au.

vk

v 2

Vl I

+ 2

V ^V S

Далее, в правой части уравнения Беломестных–Теслевой (3) коэффициент

Пуассона ц , согласно известной формуле теории упругости [6], также является функцией отношения квадратов скоростей звука (ν² L /ν² S )

2 - ( v l Zv , )²

^Ц 2 - 2( v l Zv _s)^2.

Отмеченное выше наблюдение в отношении рассматриваемых двух формул наводит на мысль о том, что их правые части, возможно, зависят от ангармонизма за счет отношения квадратов скоростей продольной и поперечной акустических волн (ν² L /ν² S ). В самом деле, наши исследования ряда металлов, ионных и молекулярных кристаллов показали [7]: если между параметром Грюнайзена у и квадратами скоростей ν² L и ν² S в отдельности фактически нет определенной взаимосвязи (рис. 2 и 3), то их отношение ( v L ²/ v s ²). оказывается линейной функцией параметра Грюнайзена у — меры ангармонизма (рис. 4).

У стеклообразных твердых тел наблюдается аналогичная линейная эмпирическая корреляция между отношением квадратов скоростей звуковых волн и параметром Грюнайзена (рис. 5, табл. 2).

Теоретический вариант зависимости ( v _L ² / v _s ² ) от γ

На рис. 4 и 5 приводится линейная корреляция между величинами (ν2L/ν2S) и γ, полученная эмпирически на основе экспериментальных данных. Представляет интерес установление взаимосвязи этих величин с помощью существующих теоретических уравнений в данной области.

Таблица 1

Скорости звука, коэффициент Пуассона и параметр Грюнайзена неорганических веществ при стандартных условиях (p = 105 Па и Т = 298 К)

№	Элементы и соединения	Скорость звука, м/c		Отношение квадратов скоростей, ( v L / v S )2	Коэффициент Пуассона, μ	Параметр Грюнайзена, γ
		v L	v S
1.	LiF	7323	4518	2.627	0.200	1.34
2.	NaCl	4666	2755	2.869	0.243	1.46
3.	LiCl	5260	3058	2.959	0.245	1.52
4.	NaBr	3284	1885	3.35	0.270	1.56
5.	KCl	4090	2312	3.130	0.259	1.60
6.	KI	2623	1469	3.188	0.265	1.63
7.	W	5233	2860	3.348	0.283	1.62
8.	Fe	6064	3325	3.326	0.292	1.68
9.	KF	4641	2587	3.218	0.274	1.73
10.	RbI	2245	1198	3.512	0.309	1.73
11.	Co	5827	3049	3.652	0.357	1.87
12.	Cu	4726	2298	4.229	0.350	2.00
13.	Ag	3686	1677	4.831	0.379	2.40
14.	Pt	3960	1670	5.623	0.390	2.54
15.	Pb	2158	860	6.30	0.372	2.93

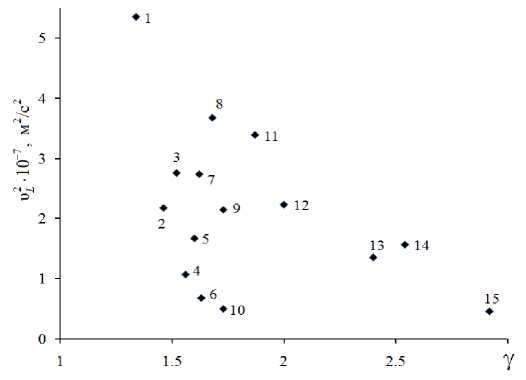
Рис. 2. Зависимость квадрата скорости продольной акустической волны ν² L от параметра Грюнайзена γ для ряда кристаллов. Номера точек соответствуют номерам веществ в табл. 1.

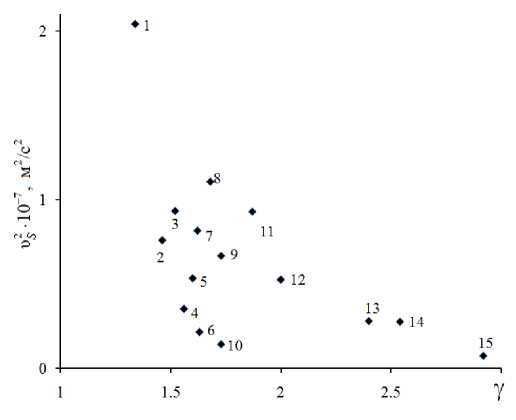
Рис. 3. Зависимость квадрата скорости поперечной акустической волны ν²_S от параметра Грюнайзена γ для кристаллов, приведенных на рис. 2. Номера точек соответствуют номерам веществ в табл. 1.

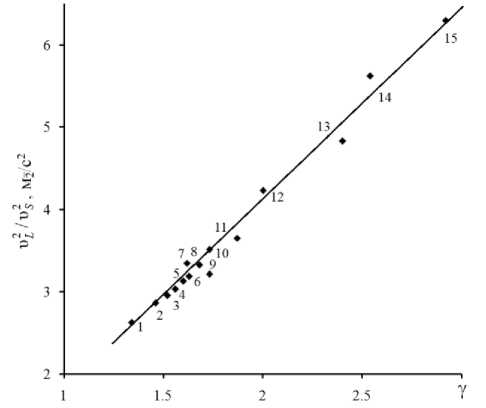
Рис. 4. Линейная корреляция между отношением квадратов продольной и поперечной скоростей звука ( v L ²/ v s ²) от параметра Грюнайзена γ для кристаллов, приведенных на рис. 2 и 3. Номера точек соответствуют номерам веществ в табл.1.

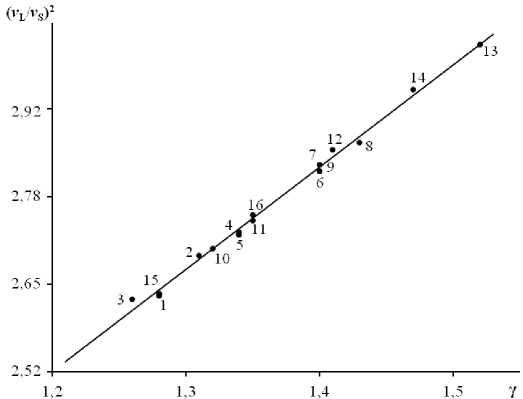
Рис. 5. Линейная корреляция между отношением квадратов скоростей распространения акустических волн ( v L / v S )² и параметром Грюнайзена γ . Натриевоалюмосиликатные стекла Na₂O-Al₂O₃-SiO₂ с разным содержанием окислов. Номера точек соответствуют номерам стекол в табл. 2.

Таблица 2

Плотность ρ, скорости распространения продольных ( v L ) и поперечных ( v S ) акустических волн, модуль объемного сжатия В А , коэффициента Пуассона μ и параметр Грюнайзена γ для стекол Na 2 O–Al 2 O 3 –SiO 2 (Использованы данные [8])

№	Состав по синтезу, мол. %			ρ ·10-3, кг/м3	ν L , м/с	ν S , м/с	B A ·10-8, Па	µ	γ
	Na 2 O	Al 2 O 3	SiO 2
1	15	0	85	2339	5430	3340	342	0.196	1.28
2	15	5	80	2358	5570	3390	370	0.206	1.31
3	15	10	75	2410	5697	3510	386	0.194	1.26
4	15	15	70	2465	5737	3469	416	0.212	1.34
5	15	20	65	2428	5850	3540	425	0.211	1.34
6	15	25	60	2472	6000	3568	470	0.226	1.40
7	25	0	75	2439	5280	3140	359	0.226	1.40
8	25	5	70	2455	5480	3240	394	0.231	1.41
9	25	10	65	2461	5610	3330	411	0.228	1.40
10	25	20	55	2470	5680	3450	405	0.208	1.32
11	25	25	50	2499	5790	3490	432	0.215	1.35
12	25	30	45	2519	6026	3556	490	0.233	1.43
13	35	0	65	2497	5340	3070	398	0.253	1.52
14	30	5	65	2486	5500	3200	413	0.244	1.47
15	20	15	65	2450	5670	3490	390	0.195	1.28
16	17.5	17.5	65	2447	5746	3458	418	0.216	1.35

Формулу для зависимости отношения скоростей звука (ν² L /ν² S ) от параметра Грюнайзена γ можно вывести из двух экспериментально оправданных соотношений, а именно из уравнения Беломестных-Теслевой (3) и формулы теории упругости (5), связывающей квадраты скоростей акустических волн с коэффициентом Пуассона μ, которую разрешим относительно (ν² L /ν² S ) и запишем в виде [6]

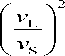
2 - 2ц

1 - 2ц

Выразив из уравнения Беломестных-Теслевой (3) коэффициент Пуассона μ через γ и подставив его в формулу теории упругости (6), приходим к следующей зависимости отношения (ν² L /ν² S ) от γ

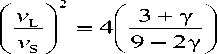
Такой же результат можно получить также из формулы Беломестных для акустического параметра Грюнайзена (соотношение (1) в работе [3]).

Теоретическая зависимость (7) находится в согласии с экспериментальными данными для стекол — прямая на графике проходит практически через начало координат с тангенсом угла наклона, равным единице (рис. 6). Исследованные кристаллы (табл. 1) в целом подчиняются зависимости (7), однако они по отношению к ней делятся на две группы, каждая из которых описывается уравнением прямой, не проходящей через начало координат (рис. 7, а, b),

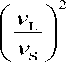
I 3 + Y = a I -------

1 9 — 2Y

+ b где а и b — постоянные (а ≠ 4 и b ≠ 0)

Возникает, естественно, вопрос, как согласовать соотношение (7) с эмпирической линейной корреляцией, наблюдаемой между величинами (ν² L /ν² S ) и γ (рис. 4 и 5.). Из формулы (7) можно получить приближенную линейную зависимость (ν² L /ν² S ) от γ при условии 2γ << 9

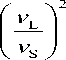
1.3 + 0.4y

Если для рассмотренных стекол, у которых γ ≈ 1.2–1.5 (табл. 2), данное условие более или менее приемлемо, то для исследованных кристаллов (табл. 1) оно выполняется с натяжкой. Этот вопрос требует дальнейшего исследования.

Заметим, что согласно формуле (7), соблюдается условие (9 — 2γ) > 0, откуда γ < 4.5, что совпадает с максимальным параметром Грюнайзена при полиморфных превращениях в кристаллах [9].

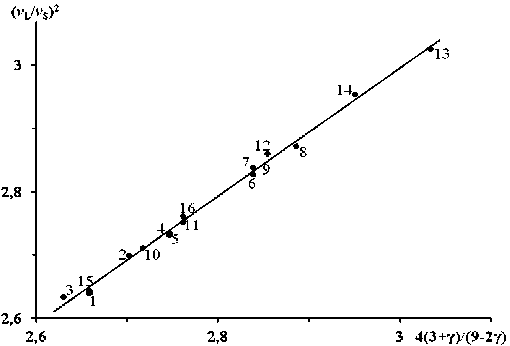
Рис. 6. Зависимость квадрата отношения скоростей распространения продольной ( v L ) и поперечной ( v _S) акустических волн ( v _L/ v _S)² от параметра Грюнайзена γ в координатах, соответствующих уравнению (7). Натриевоалюмосиликатные стекла Na 2 O-Al 2 O 3 -SiO 2 с разным содержанием окислов. Номера точек соответствуют номерам стекол в табл. 2.

С точки зрения интерпретации полученных результатов на микроскопическом уровне представляет определённый интерес модель случайно упакованных атомов в виде сфер, взаимодействующих друг с другом в месте контакта двумя взаимно перпендикулярными силами нормальной к плоскости контакта f n = k n x n и тангенциальной (силой трения) f t = k_tx_t [10]. В рамках данной модели Берлина-Ротенбурга-Басэрста (БРБ) коэффициент Пуассона ц определяется отношением тангенциальной k_t и нормальной k n жесткостей межатомной связи к = ( k_t / k n ) [10]

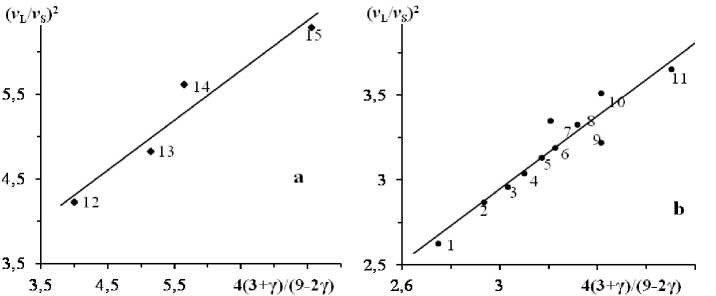
Рис. 7. Зависимость ( v L / v S )² от параметра Грюнайзена γ в координатах, соответствующих уравнению (7). Номера точек соответствуют номерам кристаллов в табл. 1.

1-λ µ=

4+λ

Из соотношений (6) и (9) следует, что отношение квадратов скоростей (v²_L/v²_S) определяется микроскопическим параметром к

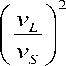
=2(3+2

2 + 32

В свою очередь, как видно из равенств (3) и (9), параметр λ однозначно связан с ангармонизмом (γ).

Заключение

Таким образом, квадраты скоростей продольной и поперечной акустических волн ν² L и ν² S в отдельности практически не связаны с ангармонизмом — не коррелируют с параметром Грюнайзена, а их отношение (ν² L /ν² S ) оказывается ангармонической (нелинейной) характеристикой твердых тел. В формуле Леонтьева (2) и Беломестных-Теслевой (3) нет противоречия, касающегося взаимосвязи гармонических и ангармонических величин. Как левые, так и правые части равенств в этих соотношениях зависят от нелинейности силы межатомного взаимодействия — ангармонизма, мерой которого служит параметр Грюнайзена γ. Отношение (ν² L /ν² S ) определяется отношением тангенциальной и нормальной жесткостей межатомной связи λ = ( k_t / k_n ), которое является однозначной функцией параметра Грюнайзена.