Нелинейные дифракционные искажения оптической функции отклика в кодирующих сопряжениях оптико-электронных датчиков

При проектировании оптико-электронной датчиковой аппаратуры, содержащей кодирующие сопряжения в составе подвижной кодирующей шкалы (КШ) и неподвижных считывающих элементов (СчЭ), в большинстве случаев возникает необходимость учета погрешностей преобразования, создаваемых нелинейностью функции отклика СчЭ, проявляющейся из-за дифракции света на отверстиях КШ [1-3]. Задача о дифракции света на прямоугольном и круглом отверстиях в общем виде решена в работах [1, 4, 5]. При постановке и решении практических задач наибольший интерес представляет описание функции отклика при дифракции света на отверстиях прямоугольной и квазипрямоутольной форм (сектор кольца, овал, двояковогнутый квазипрямоугольник и т. д.) с учетом погрешностей изготовления, перекоса и смещения КШ относительно СчЭ. В процессе учета и коррекции дифракционных поправок может ставиться дополнительная задача сокращения числа вычислительных операций.

гоиСмиТрйм влияние дифракции на оптическую функцию отклика, несущую информацию о перемещении а_х (рис.1) на примере прохождения параллельного пучка света через прямоугольное (квазипрямоугольнос) отверстие КШ.

Параллельный световой поток Ф_о от осветителя падает на КШ 1. При линейном перемещении а_х КШ происходит амплитудная модуляция светового потока, падающего на неподвижный считывающий элемент (СчЭ) 2. В зависимости от типа и габаритов датчика, предъявляемых к нему требований по разрешающей способности и отношению сиг-нал/шум, выбираются те или иные геометрические соотношения между окнами КШ и СчЭ. Примем характерные для кодирующих сопряжений (КС) двухотсчетных преобразователей с амплитудной интерполяцией функции отклика параметры КШ и

СчЭ: я=а_<г=п₍/2=5О....5ОО мкм, 6>^200.... 1000 мкм. где a, b, a_d) b_d, -ширина и высота окон КШ и СчЭ соответственно, а₀ - период КШ [1,2].

Рис. 1. Схема прохождения света через кодирующее сопряжение

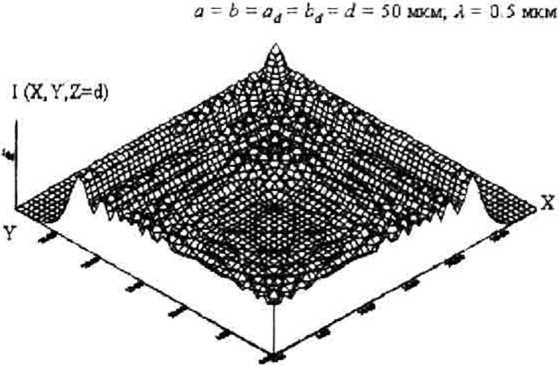
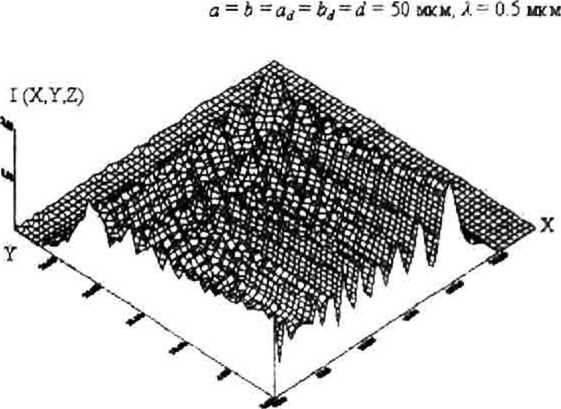
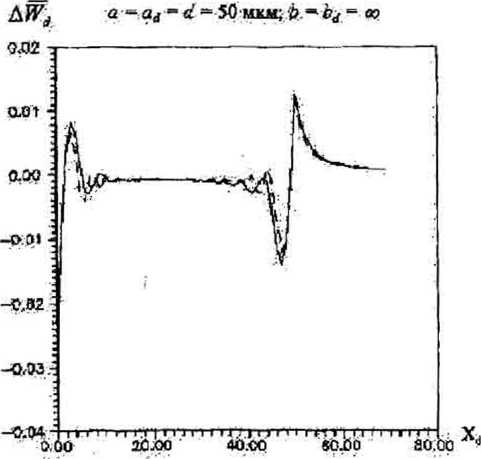
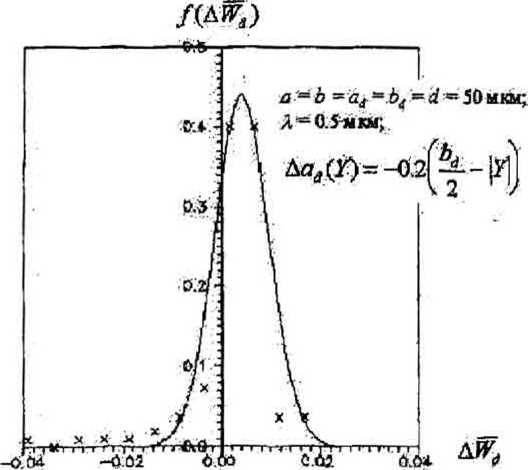
На рис. 2.а показана картина распределения интенсивности света по поверхности СчЭ в пределах одного квадранта при отсутствии (пунктирная линия) и наличии дифракции. На рис. 2,6 линией 1 показан сигнал на выходе СчЭ при идеальных формах отверстий, отсутствии шумов источника излучения и фотоприемника, и расстоянии от КШ до СчЭ Ю0. Так как в реальных КС с учетом торцевых биений в направляющих перемещения КШ =5...500 мкм, то функция отклика - амплитуда сигнала на выходе СчЭ (рис. 2,6, линия 2) - имеет ярко выраженные нелинейные участки в основаниях и вершинах “треугольников”, вызванные дифракцией. Линией 3 показан график разности между значениями функций отклика при отсутствии и при наличии дифракционных явлений (нелинейность функции отклика). При аналого-цифровом преобра- зовании нелинейность создаст ограничения по количеству достоверных разрядов кода перемещения [2]:

„ =log2(^^=.)-i                   (1)

где Н_тах Н^_п - максимальное и минимальное значения сигнала h(a_x^ на выходе СчЭ, а ДН_тах(ах) - максимальное значение нелинейности функции отклика.

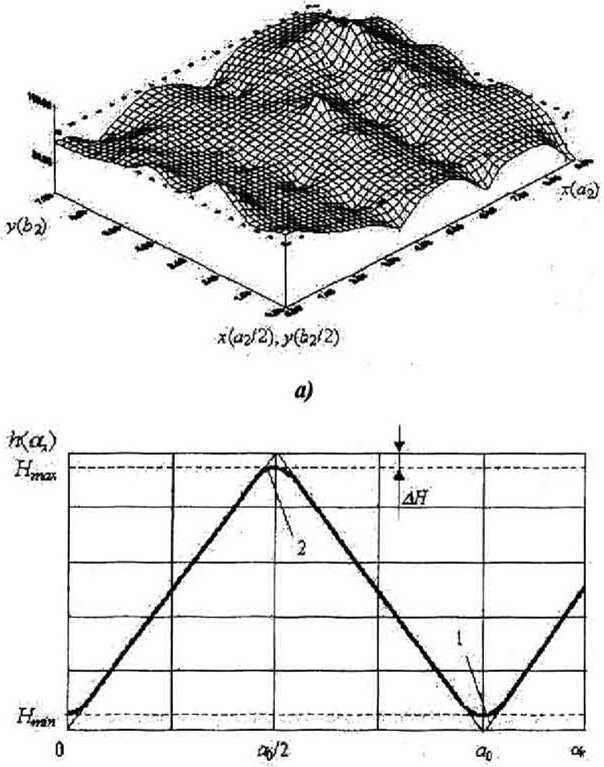
Рис. 2. Формирование сигнала на выходе СчЭ: а) распределение интенсивности света по поверхности СчЭ; б) расчетная функция отклика (1 - без учета дифракции; 2 - с учетом дифракции)

Наибольшая нелинейность регистрируемого сигнала проявляется при малых линейных перемещениях а_х относительно вершин и оснований позиционных сигналов. В некоторых случаях нелинейность может превышать амплитуду сигнала. Тогда функция OxQi) становится многозначной, а погрешность измерения становится сравнимой с самой измеряемой величиной, что приводит к метрологическому отказу датчика [6].

Характер возникновения нелинейности вследствие дифракции светового потока на достаточно широком прямоугольном отверстии, а также погрешности, возникающие из-за искажения формы отверстия, можно оценить, пользуясь математическим аппаратом, описанным в [5]. Целью настоящей работы является исследование влияния дифракции светового потока на КШ и СчЭ на амплитуд} регистрируемого сигнала h(x) с учетом инструментальных погрешностей и формирование рекомендаций по разработке способов учета и ком пенсации возникающих при этом нелинейных искажений.

• 2.    Основной формализм

При конструировании сверхминиатюрных оптоэлектронных датчиков перемещений возникает задача расчета оптической функции отклика h(x). Поскольку1 реальные геометрические размеры окон датчиков соизмеримы с расстоянием от КШ до СчЭ и не более, чем на 1-2 порядка превосходят длину волны падающего света, необходим корректный учет влияния дифракции на результаты измерения. В рассматриваемом случае мы имеем дело с дифракцией Френеля, несмотря на то, что падающую на КШ световую волну можно считать плоской; детально этот вопрос освещен в работе [5].

Используя обозначения работы [5] представим комплексную амплитуду Up дифрагированной волны в точке р(х, у, z) наблюдения в следующем виде (см. рис.1):

yH^exrt,M)'<’             <2)

где Я = ,pX^xyT(Y^yUHZ^zy , X, Y, Z -координаты точки наблюдения Р, х, у, z - координаты точек волновой поверхности, a dfn - элемент проекции площади df на плоскость, перпендикулярную к направлению падающего луча. Для прямоугольного отверстия, имеющего ширину а и ,                                    а           а длину о выполняются соотношения--5 х < —.

b          b        _

— < у < —; z = 0.

2          2

В случае нормального жтоомагнитной    волны

падения плоской на указанное прямоугольное                         отверстие

U = Uti * exp kikz^ = Uo = const (т.к. z=0) и выражение для амплитуды сильно упрощается:

kU0 4 4

U_pkX, Y, 2^ = —— | dx J dy x

"% "% exp^X - x)2 4- (У - у)2 4- Z2")

^X - x)² + (У - y)² 4- Z²

Основная идея метода стационарной фазы состоит в том, чго интеграл (3) набирается, в основном, в окрестности нуля первой производной от показателя комплексной экспоненты. В окрестности этой точки квадратный корень в показателе экспоненты можно разложить в ряд Тейлора с точностью до квадратичных членов:

^Х - х)² + (У - у)² 4- Z² *

~ Z + 1 (£2^НУ^у/ •       <4>

2          2

В этом приближении

UAX, Y, Z^ « --- L . exp №) x ^p             TniZ

U (X, Y, Z^ * *5—. . cos О • exp f*Z) х ^р          'ЫА

4      f ЩХ - X)² )

x dx exp  x

-%I )

4      f щу - у)²)

X dy exp ---—I

У dx exj ik_tx + ik

x | dyex^ ik_vy + tk

Переходя к новой переменной интегрирования

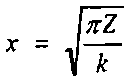
CV - x)² "

2Z

(Г - y)' 2Z

(H)

где 0 - угол между направлением падающего луча и плоскостью ху, в которой лежит КШ.

Амплитуда (II) выражается через интегралы

Френеля:

I7АХ, У, Z) = ^- • соз0 х

учитывая, что dx = J— ' di, пределы интегриро вания задаются неравенством

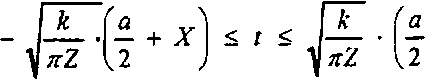
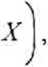
используя для переменной у совершенно аналогичную подстановку, получаем окончательный результат:

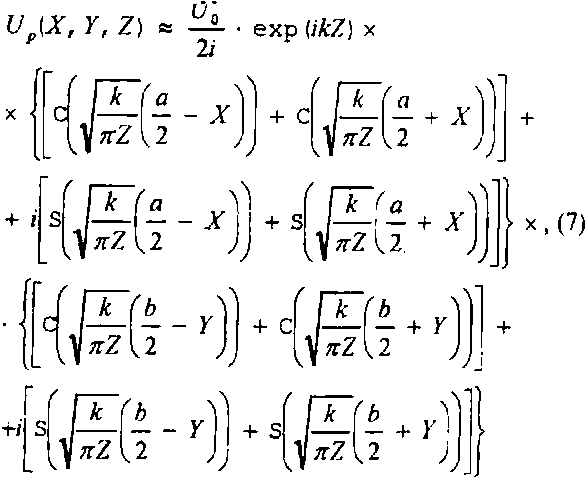
где C(z) и S(z) - стандартные интегралы Френеля |4|

C(z) = [ cos (— tT^dt,(8)

о

S(z) = [ sin (— t2)dt.

о

Рассмотрим наклонное падение плоской волны на КШ Амплитуда падающей волны является функцией координат:

I/ = Щх, у, z = 0) = U_o ■ ехр{(£ ■ г) (Ю) и ее нельзя выносить из-под знака интеграла.

В этом случае выражение (5) модифицируется:

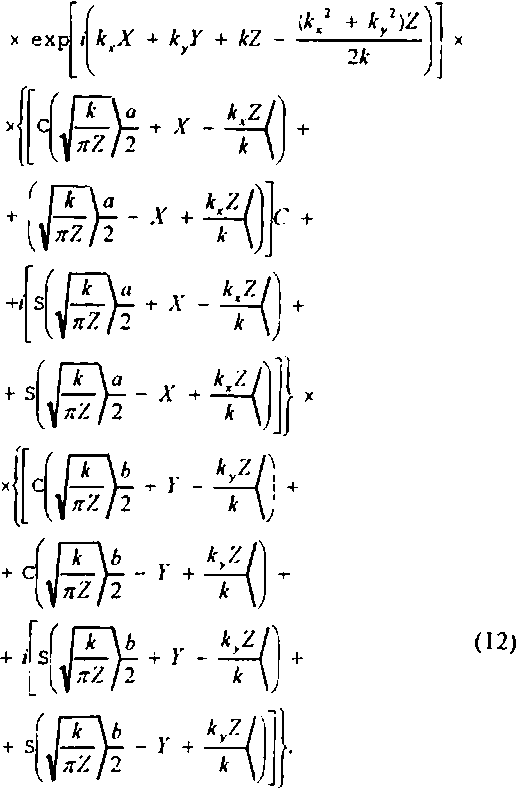
Введем переменные

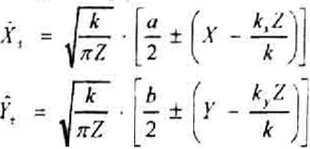
Тогда интенсивность дифрагированного на прямоугольном отверстии света, равная квадрату модуля комплексной амплитуды, принимает вид:

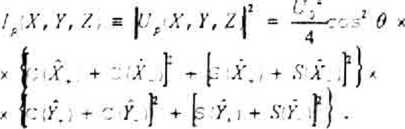
Для расчета дифракционной картины от квази-прямоугольного отверстия воспользуемся методами теории возмущений Перепишем выражение (II) для невозмущенной амплитуды Upo (случай дифракции

монохроматической световой волны на отверстии прямоугольной формы) в следующем виде: lvx- ^М Hi - И+4 “ (ь \(ь    )          ’ (14) х Щх, у,0) J 4^- ~ ^J®^ + ^j х 4<Х - х)2 + (У - у? + z1 где 0(х - ступенчатая функция Хевисайда [7]. Возмущенная амплитуда отличается от невозмущенной амплитуды (14), за счет вклада участков волновой поверхности, не содержащиеся в исходном пря-моутольнике - — <  х < —\ - — < у < —. Учтем вклад от этих участков волновой поверхности в амплитуду дифрагированной волны. Для случая реальной формы краев щели имеем: иДХ, У, Z) = j dx j dyUkx, У,^ X © — + 5ПО(У) - X© — + X - £aO(v) x U      Д2      ) -г ©(у + б^кх^ - yj®^ + у - Vto)x exp^k^kX - xy 4- (F - y)2 + z2) «jkX - x)2 + (F - y)2 + z2 Здесь форма правого края отверстия описывается уравнением х = — + биаку , левого края- уравнением х = - — + бмку , b      г , верхнего- уравнением у = — + б^аку , а нижнего - уравнением у = - у + б.аку^ Y Очевидно, что разность между возмущенной и невозмущенной амплитудами имеет вид: 6UpkX, У, Z^ =UpkX, У, ZV ирДХ, У, Z) = = -^- [ dx ( сМ-Цх, уг0)х 2яД Д х Jof — + д"па(у) - х |©| — 4 х - ^.а(у)| х fb          Mb          )       <16) х © — + б^Ькх} - у 1© — + у - бнЬкх) - <2              /                  ) _ ©Г— - xW — +      - y)©f— +

Величина возмущения 6U р легко вычисляется с помощью методов теории обобщенных функций. Производная функции Хевисайда пропорциональна б - функции. Поэтому для правой границы отверстия КШ выполняется приближенное равенство: ~ + ^04 - х 1         - х 1        - х 1 - дпй(у) (17) Аналогичные соотношения выполняются на остальных границах отверстия в КШ. Согласно определению 5 - функции J 6W ■ №dx = /(0                (18) Ограничиваясь в разложении (17) линейными членами, получаем: к бидх, У, ZM —х ₽                  2тг/ (»/2          (а     \ xj J ^пй(у)С? — , у,0 X [-6/2        U     ) ехр^к^Х - а/2^ + (F - у)2 + z2) ^ - а/2)2 + (F - у)2 + z2 - j dy5xa№T(- ^-, у,(Л -ь/1         к 2     у expl^k^X + п/2)2 + (F - у)2 + z2) л[^Х + а/2)2 + (F - у)2 + z2 «/ 2            f Ь \ + | £бс5в6(х)(; х, — ,0 к -0/2         к 2 J ехр^к^Х - х)2 + (F - /?/2)2 + z2) ^Х - х)2 + (F - b/2? + z2 [ бхбнЬ^А х, --,0 к J п  111 -о/2          V    z / ехр(' к^Х - х)2 + (F + Ь/2? + z2)l -    (19) ^Х - х)2 + (F + b/2f + z2 ! Для важного (с точки зрения синтеза КШ) частного случая дифракции монохроматического света на симметрично деформированной щели (баАу^ = -&.(у) = баку ^ба^х) = ^я.(х) = 0) выражение для возмущения амплитуды 5U принимает пригодный для численных расчетов вид:

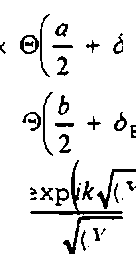
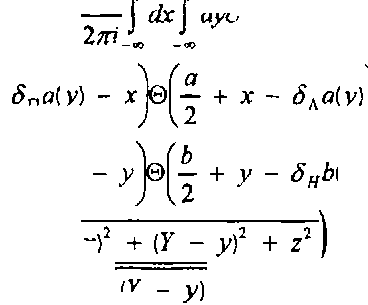
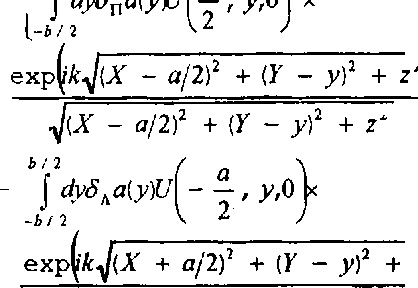
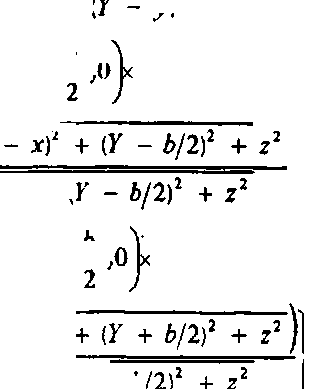
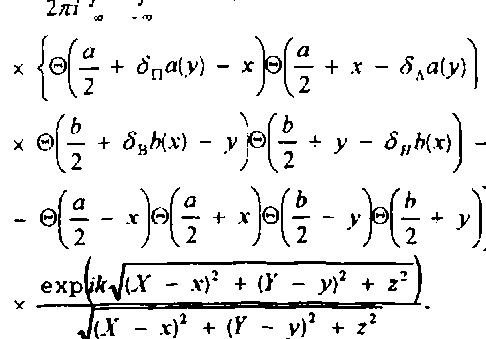
b

5L\X, Y, Z) = I dySa(y) exo №vy) x exp / к

I x 2

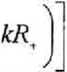
-(20)

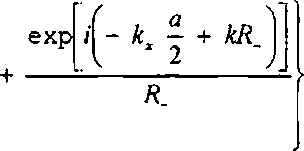
где R_t = ^X ± a / 2)² + (У - y-)² 4- 7? .

Отметим, что полученные соотношения обобщают результаты работы [9].

Исследование выражения (20) позволяет оценить влияние формы отверстия в КШ на линейность оптической функции отклика СчЭ.

• 3.    Формирование функции отклика считывающего элемента Оптическая функция отклика h(Xa) опреде

ляется очевидным соотношением:

*Ю = /^Д^У)- 1Д, Y, Z)ds_n,       (21)

Sd где р^Х, У) - функция распределения чувствительности СчЭ по его поверхности, a dsn - проекция элемента площади СчЭ ds на плоскость, нормальную к направлению падения светового луча (см. рис.1).

Для простоты рассмотрим нормальное падение света на КШ и ограничимся в расчетах случаем ф(ХЛ>\,Х е \X_d -^,X_d ^ ^-1, к 2            2 )

Исследуем одномерный предел для случая дифракции монохроматического света на сильно вытянутом прямоугольном отверстии (предельный переход b, b_d -> ос ;

[: (УД + с (У.)]2 4- ^ (УД + s (У)]2 -> 2 в интенсивности (13), то есть, дифракция на щели).

В этом приближении hLX_d4 = MVX_d , где Ид - полная энергия светового потока, попадающего на СчЭ. есть функция его координаты X_d:

U 1

Hd'x/. -

X ' f {: X .) 4- С X )f 4- ^ Xj + S X. f ^ X,-aJl

Введем безразмерные переменные:

Еа-;£=

^nZ' •° л/ 2

^ ~ ^ ^Z ^J 2            л-Z k

Тогда интенсивность света на поверхности СчЭ определяется выражением:

"У, Z) = ^i х

X jc (f „+ Е- ^ + с if,- #+ Af)f +, (23)

• 4-    [s (£₀4- q- AZ) 4- S (£₀- Z+ Д^)]²} а функция отклика имеет вид:

^ = Т^«*

X $c^_n4- Z- МЧ + С(£_о- Z+ Д£)Р 4-.   (24)

+ [s(£₀+ Z- Д£) 4- S(£_o- Z+ Д£)Г}

_,                              ,., Ij 1 1        I ЛЛ

• Введем обозначения И ₀ = —— J— .

°   2 М wax;, = f = Е- ДЕ

Безразмерная оптическая функция отклика запишется как:

^х,) = If ^ , х {с(#,+ С; + С1Е0- Д +.            (25)

+ |s(^₀4 Z) + S(£_o- ?)р}

Для подробного исследования аналитических свойств функции отклика воспользуемся четностью подынтегральной функции и введем вспомогательную функцию двух безразмерных поименных Й#„ п :

|zKo- nl =f ^ х х {: ($,+ © +;C^f-<5)f+.           (26)

+ [si#0+ f) + S(^,-

В рамках использованных допущений безразмерная оптическая функция отклика выражается через функцию lz^0, ?/

|Т,(Т,) = ^И#,,?.; - (':#„?)].       (27)

Интегрируя по частям выражение (26), получаем:

^О, ^1 =^.^0/ иЧ - Д1'(^о* п •           (2^)

В формуле (28) использованы обозначения:

J?4or ПЧ =2z/{c^₀- Z) * е^₆- ^

- [S(^„+ Z4 + S(^_o- £)]²}

п

ЛИ# „9) = 2р£. Е^Е^Е ,        (30)

-z?

н;0,;) = [ci;0+ ;i + ci;0- ;ip x

X

cos у (£0+ £)2

cosy ^0- O2

+

+ [5^o+ £) + S(£0- £)]2 x

x

Sin—(^q+^) -Siny(£₀-£)

С формальной точки зрения задача выражения оптической функции отклика через специальные функции математической физики сводится к вычислению интеграла (30). В результате весьма громоздких, но несложных вычислений, мы приходим к следующему выражению для ДИ£₀' Л ^:

2/ 3

Д^„ 7> = — fata, №-а(32)

• - В_хка,-р^ - В₂ка, Р) + ВДа,-р^

В формуле (32) и далее использованы следующие обозначения:

а-^ЕЛ 3=-^,(33)

29 о

Вра, р} = J dt sin at^!_xt - 2 + 2/?) о

2 dt

ВДа, Р) = j — sin aid - 2 + ip о ¹

Функция Вра, P выражается через интегралы

Френеля:

„    „ cos акр- I)²

Вра, Р} = ------------ х

£ о х [s(=,(l + Д)) + sfc„(l - Д)] -              ■ (35)

- ^Ч^ К^-^Ь =(;.

Функция ВДа, р^ представляет собой интеграл от комбинации элементарных функций и по трудоемкости вычислений эквивалентна любой специальной функции математической физики. Строго говоря, она не может быть сведена к конечной комбинации специальных функций. Однако, замена в (34) верхнего предела интегрирования на ос позволяет получить асимптотическую оценку В₂ка, р для В₂ [а, р}:

ВДа, р^ = В₂ка, Р) - М3 Да, р , где

ЯГ^ Д) = 1 [1/2 - екЕ^р- 1)) -

- s'teod-и) +                   ..    (36)

+ с(;„(Д- 11) + s(E,tp- 1))]

При замене ВДа, Р^ на В₂ка, Р можно пренебречь малым интегралом:

ЬВДа, р} = j — sin atkt - 2 + Ip .   (37)

Малость интеграла (37) обусловлена тем, что он имеет порядок 1 / 8а, а параметр я • а² а = ——— » 1 численно велик (характерные размеры установки делятся на длину волны падающего света).

Вместе с тем в прецизионных оптико -электронных датчиках снижение точности преобразования (25) часто ухудшает работу всей измерительной системы, вплоть до метрологических отказов [6]. Одним из источников погрешностей расчета оптической функции отклика в некоторых случаях является пренебрежение вкладом поправки М3 Да, р . При необходимости повышения точности расчетов функция ВДа, р} может быть вычислена с помощью квадратурных формул Симпсона или Гаусса. Однако, численный анализ быстроосцилли-рующих функций всегда вызывает определенные математические затруднения и большие затраты машинного времени. Быстрота и точность расчета функции отклика особенно важны для датчиков, осуществляющих автокоррекцию погрешностей преобразования в реальном времени. В связи с этим возникает ряд проблем, связанных с технологическим компромиссом быстрота - точность. Изложим один из наиболее эффективных подходов к решению этой проблемы, разработанный в работе [8].

Представим функцию ВДа, р} в следующем виде:

Вра, р^ = где [7]:	А (Л ^ + АДр, q ,	(38)
АДр, q) =	\ dt .        г J — sin pt cos qt , о *	(39)
АДр, q^ =	dt             2 . | — cos pt sin qt , 0 1	(40)
р = 4а;	q = 4a - kP - 1).	(41)

Таким образом, решение задачи сводится к построению быстрого алгоритма расчета интегралов специального вида (39) и (40).

Разложим экспоненту от мнимого аргумента в ряд по сферическим функциям Бесселя j„(y :

ехр( iyt) = £ /”(2п + 1) jjy,) Р_я(г), (42) где ?Д1 - полином Лежандра [7].

Учитывая, что cos (v/) = Re(exp(z>Z) , представим интеграл (39) в виде быстро сходящегося ряда:

АДр, 9) = Е (-Гол + 1) ^„kqty^p . (43) где

Ф1„(Р) = f — sin pt² P₂„(Z) •   (44)

о 1

Аналогично вычисляется интеграл (40):

АДр^ = £(-1)^п(4я + 3) Ъ_п*м>1„-\1р^ (45) п=0 где

• ¹ dt

• 4.    Результаты расчетов

<Р1п^Р^ = f "Г ^COS ^^{2 Р}2л ₊ 1<^Г)'         (⁴⁶)

На практике сходимость рядов (43) и (45) наступает при и > q. Поскольку измерительная информация содержится в параметре q. то коэффициенты (р ₂„( р) и ^_2n__t(p , определяемые формулами (44) и (46), вычисляются заранее. Для расчета сферических функций Бесселя используется быстрый алгоритм, предложенный в работе [8].

Конкретные расчеты показывают, что время вычисления интегралов (39), (40) сокращается более, чем на порядок, по сравнению со временем, затрачиваемым на их прямое вычисление на основе квадратурных формул типа Симпсона или Гаусса. Алго-ритм (44)-(46) может быть использован для схемотехнической автокоррекции нелинейности функции отклика для правильной прямоугольной формы отверстий КШ и СчЭ с точностью до 1...2% (точность приближения Кирхгофа |9]) в реальном времени.

Формулы (26) - (46) полностью решают задач} нахождения оптической функции отклика для случая, когда и отверстия в КШ и СчЭ имеют правильную прямоугольную форму.

На основе изложенного выше математического формализма был создан пакет прикладных программ, позволяющий имитировать формирование функции отклика в оптико - электронных датчиках.

На рисунке 3 представлены результаты расчета фрагмента дифракционной картины от квадратного отверстия в КШ для нормально падающего монохроматического света. Хорошо заметны всплески интенсивности света у краев отверстия.

Глубина модуляции растет с увеличением расстояния d между КШ и СчЭ, а дифракция Френеля плавно переходит в хорошо исследованную дифракцию Фраунгофера.

На рис. 4 представлен результат расчета для случая, когда отклонение границы отверстия КШ от прямой линии задается функцией баку*! = -0.05 ■ (— - W мкм и уменьшает эффективную площадь отверстия

Рис. 3. Дифракционная картина от нря.чоугольного отверстия

Рис. 4. Дифракционная картина от квази прямоугольного отверстия

Из рисунка 4 видно, что малые возмущения формы прямоугольного отверстия, обычно связанные с технологическими погрешностями изготовления КШ, увеличивают амплитуду всплесков интенсивности на краях Отсюда следует, что изменение формы отверстий в КШ малоперспсктивно в смысле линеаризации функции отклика

Гораздо более перспективным представляется направление, связанное с изменением формы ( чЭ Дело в том, что возмущение прямолинейной формы краев СчЭ приводит к эффективному усреднению амплитуды регистрируемого оптического сигнала Хорошо известно, что средние значения (по интервалу значений аргумента.) от быстроосциллирующих функций обладают существенно более приемлемыми свойствами, по сравнению с исходными нсосрсд-ненными функциями, с точки зрения возможности их аппроксимации плавными кривыми. На рис. 5 приведены результаты расчетов оптической функции отклика и се кусочно - линейных аппрокси.ман-тов для случая квазипрямоутольной формы СчЭ. На рисунке 6 показаны зависимости разности между оптической функцией отклика, вычисленной в приближении Кирхгоффа, и ее линейным и кусочно - ли- нейными аппроксимантами. Точность данной аппроксимации достаточно высока: абсолютная погрешность не превосходит 0.04.

Рис 5. Сплошная кривая - функция отклика для прямоугольного отверстия вКШ

^vW^ _а =k = Оу —Ъ^ = zZ - 50 мкм; 2=50 мкм

0.04

0.03

0.02

0.0.1

0.00

-0.01

-Q.02

Рис 6 Сплошная кривая - разность между оптической функцией отклика, вычисленной в приближении Кирхгофа и ее линейной аппроксимацией

_        у

Wd = 1--—. Штриховая кривая - то же для ad кусочно-.линейной аппроксимации

СчЭ имеет форму искаженного квадрата. Отклонение границы СчЭ от прямой линии задается

^Y) = -0.2 <^- - |Г|

функцией

мкм и

уменьшает эффективную площадь чувствительной поверхности. Штриховая кривая соответствует кусочно - линейной аппроксимации

Wda = 0.93 ■ (1 - 1.07 • ^ + Д(Ху , ad где

|Д(Ху) = 2.5 • 10 ⁴ • X_d 10 < X_d< 50

|А(Ху) = О        X_d< 10; X_d > 50

Г/ = 0.93 • (I - 1.07 • X_d / a_d^ + Д(Ху , где

[д(Ху) = 2.5 • 10 ⁴ . X_d    10 < X_d< 50

(Д(Ху) = 0        X_d< 10; X_d > 50

Автокоррекция дифракционного вклада в нелинейность W_dlX_d возможна также на основе нелинейной аппроксимации кирхгофовской функции отклика:

iV^Xj, = 0.93 ■ (1 - 1.07 • ЛЛ) +

+ £ ^W /=1

|Д,(^> = -0.0008 ■ (X, - 7)² [Д№) = О            X,

(47.1)

Д,«,1 = -X X, > 50

Д₂(Ху) = о X_d< 50

[Дз^^г^-мг4.^ ю^Ху <50 [дз(Ху) = 0        Ху <10; Ху >50

(47.3)

W ⁼ 0.008. expf-S^]^

Д4(Ху) = О Ху > 10

Ху < 7 а 7

(47.2)

I Д5(Ху) = 0.006-Ху-0.286, j 46.9 < Ху <50 ■ (47.5) |д$(Ху) = 0 Ху <46.9; Ху >50

Из рисунка 7 хорошо видно, что в этом случае погрешность аппроксимации удается понизить' на порядок по сравнению с линейными аппроксимантами.

Абсолютная погрешность ДЯу(Ху) аппроксимации (47) составляет менее 0.005. Тот факт, что функция отклика практически монотонно убывает с ростом координаты перемещения КШ, приводит к возникновению проблемы контроля относительной погрешности измерения при малых значениях.

Рис. 8. демонстрирует рост относительной погрешности dWd (Xd) = ДИу(Ху) / 1Ту(Ху аппроксимации (47) на хвостах функции отклика, где она может достигать 30% и более, что абсолютно неприемлемо с метрологической точки зрения. Поскольку проведение точных расчетов И^(Ху) в реальном времени является весьма трудоемким, то для повышения точности и быстродействия системы необходимо исключить из анализа зоны высокой погрешности. С этой целью в КС вводятся дополнительные СчЭ, и аппаратно реализуется алгоритм синтеза функции отклика на основе логического анализа сигнала и выделения ее главной линейной части для каждого из СчЭ. Этот прием позволяет решить задачу автокоррекции нелинейности функции отклика в реальном времени.

21^ _а = b = _а^ = ь₄ = d = 50 мкм; Л = 50

Q.0Q6 т

O.OO4

Q.DQ2

0.000

-0.002

-0.004

-0.008

100 X|

III п ITU ш III III III 11 г л Iim и и i iri^ CO 30.00 4-0.00   50.00 Й0

Рис 7. Разность между вычисленной оптической функцией отклика и ее нелинейным аппроксимантом (47)

Следующим направлением, идеологически примыкающим к методам повышения точности измерения за счет различных процедур осреднения сигнала, является использование немонохроматических пучков света. На рис. 9 представлены результаты расчета дифракционной картины для двух значений длины волны монохроматического света, падающего на узкую щель. Наблюдается относительное смещение дифракционных картин и наложение минимумов одного распределения на максимумы другого распределения. Очевидно, что возможен подбор спектрального состава излучения в КС, обес печивающего существенное сглаживание суммарного сигнала.

/₀ а. = a_d = d. = 50 мкм; b = b_d = оо

Рис. 9. Интенсивность дифрагированной световой волны

Сплошная кривая 2=0.5 мкм, штриховая кривая Х=0.9 мкм.

В простейшем случае равномерного частотного фильтра подобное сглаживание приводит к суммарной картине, представленной на рис. 10.

/уо

/_с а = a_d = d = 30 мкм; b = b_d = ®

Рис. 10. Интенсивность дифрагированного света Штриховая кривая 1=0.5 мкм

Сплошная кривая - то же самое для белого света. Усреднение производится по диапазону длин волн 0.4,<0.9 мкм.

Исследования функции отклика показывают, что при этом точность аппроксимантов повышается, а сами аппроксиманты упрощаются. Этот факт проиллюстрирован на рис. 11. где представлен расчет для дайны волны Х=0.5 мкм (сплошная кривая) и для белого света (штриховая кривая; усреднение произведено по диапазону длин волн 0.4<Х<0.9 мкм).

Рис 11. Разность между оптической функцией отклика, вычисленной в приближении Кирхгофа и ее линейной аппроксимацией

На рис. 12. представлена функция распределения величины погрешности нелинейной аппроксимации (47). Из рисунка видно, что основная доля погрешностей приходится на диапазон -0.004 < AW< 0.004, Условно нормированная огибающая гистограммы 12, описывающей распределение погрешности аппроксимации (47), имеет гауссовский вид:

г,.ш, п ЛЛ ( (Д^ - 0-004)2) = 0.44 • ехр--.

(     0.00006 J

Рис 11 Гистограмма распределения погрешностей нелинейной аппроксимации (47) кирхгофовской функции отклика

Для повышения точности расчетов необходимо учесть асимметрию и эксцесс ненормированной функции распределения f{AW . Гистограмма построена для случая прямоугольного отверстия в КШ СчЭ имеет форму искаженного квадрата с параметрами a_d = b_d = d = 50 мкм, причем

Д/г^У) = -0.2 • ^ - |У| • Длина световой волны Х=0.5 мкм.

• 5.    Заключение

Резюмируем вышесказанное следующим образом:

Выведены аналитические выражения для интенсивности ЦХ, У, Z светового потока и функции отклика h(Xd) в приближении Кирхгофа.

Получены удобные для расчета асимптотические оценки функции h(Xd), учитывающие влияния дифракции и инструментальных погрешностей.

Разработан формализм для решения задачи минимизации нелинейности оптической функции отклика.

Проведен численный анализ влияния дифракционных и инструментальных погрешностей на работу оптикоэлектронных датчиков перемещений.

Показано, что вариации формы отверстии в КШ ведут к росту нелинейности функции отклика, а вариации формы СчЭ могут привести к заметному снижению нелинейных искажений.

Продемонстрирована возможность линеаризации функции отклика за счет использования немо-нохроматичсских световых пучков с управляемым спектральным составом.

Исследовано распределение погрешностей нелинейной аппроксимации кирхгофовской функции отклика.

Предложен способ автокоррекции нелинейных искажений.

Представляется целесообразным продолжить данное исследование и обобщить результаты для случая сложной взаимодействующей системы КШ -СчЭ с целью решения задачи синтеза оптикоэлектронных датчиков перемещений с минимальной нелинейностью оптической функции отклика.

• 6.    Литература

  • 1.    Фотоэлектрические преобразователи информации I под редакцией Л.Н.Преснухина, М., Машиностроение, 1974, 375 с.

  • 2.    Домрачев В.Г., Мейко Б. С., Цифровые преобразователи угла: принципы построения, теория, точность, методы контроля. М., Энергоатомиздат, 1984, 328 с.

  • 3.    Аш Ж. и др. Датчики измерительных систем (в двух книгах), кн. 1 (2), перевод с франц, М., Мир, 1982, 480 с. (424 с).

  • 4.    Ландсберг Г.С., Оптика, М., Наука, 1976, 928 с.

  • 5.    Ландау Л.Д, Лифшиц Е.М., Теория поля, М., Наука, 1973,504 с.

  • 6.    Конюхов Н.Е., Леонович Г.И. Устройства допус-кового контроля в цифровых преобразователях перемещений для диагностики неявных параметрических отказов// Измерительная техника.-1990.-№9-С. 11-13.

  • 7.    Абрамовиц М., Стиган И., Справочник по специальным функциям, Москва, Наука, 1979, 832 с.

  • 8.    Ratis Yu.L, de Cordoba P.F., Computer Physics Communications 76(1993) 381.

  • 9.    Ратис Ю.Л., Леонович Г.И. Дифракция светового потока на чувствительных элементах волоконно-

    оптических и оптико-электронных датчиков механических перемещений// Компьютерная оптика.- 1996,-№16,-С.74-77.