Нелинейные и конструктивно нелинейные задачи в теории пластин

Интерес к конструктивно-нелинейным задачам механики упругих тел обусловлен необходимостью расчета все более сложных конструкций, встречающихся в инженерной практике. Данные задачи относятся к классу контактных задач с неизвестной областью активного взаимодействия элементов конструкций. Исследование подобного рода задач – важная проблема при анализе прочности конструкций, поскольку контактное давление является одним из определяющих видов силовой нагрузки на элементы инженерной конструкции. Достаточно полный обзор алгоритмов решения контактных задач содержится в работе Н.Г. Бураго, В.Н. Кукуджанова [1].

Рассматриваемые проблемы сводятся к исследованию вариационных неравенств. Основы теории вариационных неравенств заложены в работах Ж.- Л. Лионса, Р. Гловински, Р. Тремольера [2], Бай-оки К., Капело А. [3], а также в работе Е.И. Михайловского и В.Н. Тарасова [4]. Систематическому применению неравенств и негладких функционалов в механике посвящена монография П. Панагиотопулоса [5] и работа Г. Дюво, Ж.Л. Лионс [6]. В монографии Е.И. Михайловского [7] рассматриваются контактные задачи с неизвестной областью активного взаимодействия элементов. В частности, там приводится аналитическое решение контактной задачи системы двух параллельных балок, находящихся на некотором расстоянии друг от друга. На верхнюю балку действует постоянная нагрузка так, что в процессе деформации балки контактируют в некоторой области. Приближенные методы решения экстремальных задач в полном объеме раскрывают В.Ф. Демьянов и А.М. Рубинов [8].

В данной работе численным методом решается контактная задача для двух параллельных пластин, расположенных на некотором расстоянии друг от друга. На верхнюю пластину действует нормальная нагрузка. Для решения применяется метод обобщенной реакции, разработанный в работе [4]. Он представляет собой метод проекции градиента, примененный к двойственной задаче математического программирования. На каждом шаге предлагаемого алгоритма требуется решать уравнения равновесия пластины, что само по себе представляет достаточно сложную задачу. Преимущество данного алгоритма заключается в том, что для решения уравнений равновесия можно использовать все известные методы решения краевых задач в теории пластин. Учет ограничений в форме неравенств значительно усложняет использование пакетов метода конечных элементов (МКЭ), особенно в случае нелинейной теории равновесия. В случае использования линейной теории пластин двойственная задача выписывается в явной форме, что значительно упрощает вычисления. Однако метод обобщенной реакции успешно применен и в случае нелинейной теории пластин Кармана. Задачи такого рода могут быть успешно решены практически в любом пакете конечно-элементного моделирования, однако круг решаемых ими задач ограничивается, в основном, решением уравнений равновесия, либо уравнений движения элементов конструкций, тогда как в нашем случае требуется решать задачу выпуклой оптимизации. Применение теории двойственности в методах оптимизации всегда является довольно эффективным.

Теория двойственности и ее применение, в том числе и к задачам механики, подробно изло- жена в монографии И. Экланд, Р. Темам [9]. В работе П.С. Аронова [10] представлено решение контактной задачи теории упругости с односторонними связями методом конечных элементов. В [11] авторы М.А. Осипенко и Ю.Н. Няшин исследовали задачи об одностороннем контакте балок, струн и пластин, предложили метод построения аналитического решения, а также доказательство существования и единственности этого решения. В [12] K.A. Tzaros и E.S. Mistakidis рассмотрели задачу об одностороннем контактном изгибе непрерывных балок при наличии начальных геометрических несовершенств, представили аналитический метод, основанный на теории упругой устойчивости. Математический подход Эйлера, построенный на фундаментальном решении краевой задачи потери устойчивости непрерывных балок, авторы модифицировали с учетом условий одностороннего контакта. Кроме того, чтобы полученные аналитические решения были применимы для практических случаев проектирования, K.A. Tzaros и E.S. Mistakidis учли фактическую прочность поперечного сечения балки при комбинированном сжатии и изгибе. Реализация предлагаемого способа демонстрируется в статье на характерном примере. В статье А.В. Ермоленко [13] приведены уточненные уравнения теории пластин для решения контактных задач. В работе [14] особое внимание уделяется случаю, когда контактные ограничения налагаются упругим основанием типа Винклера, и основание реагирует только на сжатие, характеризуя контакт как односторонний. Для решения этого класса односторонних контактных задач предлагается подход типа Ритца с подвижными границами, в котором координаты, определяющие границы контактных областей, рассматриваются как дополнительные переменные задачи. Метод иллюстрируется конкретными примерами и результаты сравниваются с доступными результатами, полученными методами конечных элементов и математического программирования. Контактная задача для двух пластин одинаковой формы рассмотрена Е.В. Пяткиной в статье [15]. Там предполагается, что пластины, одинаковые по форме и размерам, расположены параллельно друг другу без зазора, и на боковых границах выполняются условия жесткого закрепления. Для решения использована модель Кирхгофа–Лява, выведены вариационные и дифференциальные постановки, рассмотрены случаи двух упругих пластин и когда одна из пластин является упругой.

Контактная задача для двух параллельных прямоугольных пластин

Рассмотрим систему из двух параллельных прямоугольных пластин, находящихся друг под другом на расстоянии р . Обозначим через w i ( x,y ) , 0 < x < a, 0 < y < b, i = 1; 2 прогибы пластин. Пусть на верхнюю пластину действует нормальная нагрузка q . Пусть для определенности выполнены граничные условия шарнирного опирания:

wi(0,y) = 0, wi(a, y) = 0, wi(x, 0) = 0, Wi(x,b) = 0, д2 wi (0,y) ∂x2

д ² w i ( x, 0) ∂y ²

Предположим,

= 0 ,

= 0 ,

что

д ² w i ( a, y ) ∂x ²

д ² w i ( x, b ) ∂y ²

= 0 ,

= 0 .

перемещения пластины

приводят к их контактному взаимодействию. Тогда решение задачи сводится к вариационной проблеме

J ( w 1 ,w 2 ) = ^ ^ D^ (A w 1 ) ² - qw 1 +

Уравнения (6) являются уравнениями равновесия элементов; второе ограничение в (6) – условие односторонности связи; последнее ограничение – условие дополняющей нежесткости, заключающееся в том, что если сила реакции r не обращается в ноль, то w 1 - w 2 - p = 0 , т.е. пластины контактируют в некоторой точке, и наоборот, если w ₁ - w ₂ - p <  0 , то r = 0 .

Решение уравнений (5) запишем в виде:

w i = G i ( q

-

r ) , w 2 = G 2 r,

+ -^2 (A w 2 ) 2 dxdy ^ min ,

при ограничениях w 1 — w2 — p < 0, (x, y) G Q, Q = [0, a] x [0, b], (3)

D i – цилиндрические жесткости пластин.

Решение задачи (2)-(3) существует в W ₂ (Q) — в пространстве функций Л.С. Соболева, имеющие обобщенные, суммируемые с квадратом вторые производные. Введем в рассмотрение функцию Лагранжа

L ( w 1 ,w 2 ,r ) = j j^ D¹^ (A w 1 ) 2 +

+ -2 2 (A w 2 ) ² - qw 1 + r ( w 1 - w 2 - p )] dxdy.

Справедливо следующее утверждение [16]: для того, чтобы функции w ₁ ^∗ , w ₂ ^∗ были решениями задачи (2)–(3), необходимо и достаточно, чтобы нашелся множитель Лагранжа r * x, y >  0 , ( x, y ) G Q , такой, что w ₁ ^∗ , w ₂ ∗ и r ^∗ были седловыми точками функции Лагранжа, т.е.

L ( w * ,w 2 ,r ) < L ( w * ,w^r * ) < L ( w 1 ,w 2 ,r* ) , (4) (вообще говоря r * ( x, y ) - не обязательно суммируемая с квадратом функция).

Справедлива теорема о минимаксе:

max min L ( w ₁ , w ₂ , r ) = min max L ( w ₁ , w ₂ , r ) . r ≥ 0 ( w 1 ,w 2 )                     ( w 1 ,w 2 ) r ≥ 0

где G1 , G2 – ограниченные линейные операторы в L2(Q). (6) будет выполнено, если сила реакции контактного взаимодействия пластин будет удовлетворять уравнению r =[r - а(G2r - G 1(q - r) + p)] +, (9) где f+ = maxa>0{0,f} = 2(If| + f) -срезка функции f. В самом деле, пусть r = 0, то получим w2 + p < w 1. Еслиже r > 0, тогда G2r-G 1(q-r)+ p = 0, т.е. w2 + p = w1 .

Обозначим ( f,g ) = J J f f ( x,y ) g ( x,y ) dxdy -скалярное произведение в L ₂ (Q) . Подставляя (8) в функционал Лагранжа (4), с учетом граничных условий (1) найдем явное выражение для функционала F ( r ) .

j j -2- (A w ₁ ) ² dxdy = j j -2 ¹ AA w ₁ -w ₁ dxdy = = УУ |( G 1 ( q-r ) , q-r ) dxdy = |( G 1 ( q-r ) , q-r ) ,

[ [ D ² (A w 2 ) ² dxdy = |( G 2 r,r ) ,

J J f ^{2 2}

F ( r ) = - 2( G 1 r,r ) -

⁺⁽ G 1 ^q,r ) ^{+ (} p^,r ) ^-

2⁽ G 2 ^{r,r ) +} |⁽ G i q,q ) .

Для отыскания седловой точки функционала Лагранжа необходимо решить задачу

F ( r ) ^ min ,

r≥0

Задача минимизации функционала по w ₁ , w ₂ приводит к системе Эйлера

{

₁ AA w ₁ = q - r, ₂ AA w ₂ = r.

Проблема F ( r ) ^ max и задача (2)-(3) являются парой двойственных задач выпуклой оптимизации. Наряду с уравнениями (5), необходимо рассмотреть условия, которым должны удовлетворять перемещения w 1 , w 2 ,

где F ( r ) = -F ( r ) .

Сформулируем несколько теорем из теории экстремальных задач [8]. Пусть M ∈ L ₂ – выпуклое, замкнутое, непустое множество, f ( r ) - непрерывно дифференцируемый функционал, f ‘ ( r ) - производная функционала f ( r ) . Пусть r G L ₂ - некоторая точка, v ( r ) = P M ( r ) - проекция точки r на множество M , т.е. решение экстремальной задачи

I ^{||v ( r} ) ^{- r|}| ² = ^min| ^||v 2              v G M 2

-

r|| ²

{w 1 - w 2 - p < 0, r > 0,

r [ w 1 - w 2 - p ] = 0 .

Введем в рассмотрение функционал

F ( r )= min L ( w 1 , w 2 , r ) .

( w 1 ,w 2 )

есть ближайшая точка множества M к точке r . Такая точка существует и единственная. Пусть а >  0 , ш ( r ) - проекция точки r - af ‘ ( r ) на множество M, т.е. ш ( r ) = v ( r - af ‘ ( r )) .

Теорема 1. Для того чтобы r ∗ была решением задачи

f ( r ) ^ min r ∈ Ω

необходимо, а в случае выпуклости f ( r ) , и достаточно, чтобы г * была неподвижной точкой отображения ш ⁽ r ) :

r * = ш ( r * ) = v ( r * — af ‘ ( r * )) .        (11)

Производная от функционала F ( r ) имеет вид

F' (r) = G1 r + G2r + P - G1 q, а M – это множество неотрицательных функций в L2 из Q. Проекция некоторой точки на множество M в данном случае имеет вид v (r) = 2( |r| + r) = max {0, r}.

Необходимое условие (11) для задачи (10) в форме проекции градиента имеет вид

r* = (r* — a (G i (r* — q) + G 2 r* + p)+, (12) последнее уравнение совпадает с уравнением (9). Для решения уравнения (12) можно применить метод последовательных приближений. Пусть r0 – некоторая неотрицательная функция rk+1 = (rk - a(G 1(rk - q) + G2rk + P) + •   (13)

Можно показать [4], что существует a 0 >  0 такое, что при всех a G (0 , a 0 ] последовательность (13) является минимизирующей для функционала F ( r ) на M , т.е.

lim F (rk) = inf F (r), k^^       rEM и последовательность перемещений w 1 k = G 1(q — rk), w2k = G2rk      (14)

сходится к решению задачи (1) – (3). Для реализации алгоритма (11) необходимо решать уравнение равновесия пластин (5).

Рассмотрим бигармоническое уравнение

DДДw=q при выполнении граничных условий (1).

Для конечномерной аппроксимации применим метод сеток. Сеточный бигармонический оператор имеет вид:

I

ДД W ij = ДД w ( X i ,y j ) = h 4 (20 w ij —

• ^— 8⁽ w i,j +1 ⁺ w i +1 ,j ⁺ w i - 1 ,j ⁺ w i,j - 1 ⁾⁺ +2( ^w i +1 ,j +1 + ^w i +1 ,j - 1 + ^w i - 1 ,j +1 + ^w i - 1 ,j - 1 )+ + ( w i,j +2 + w i +2 ,j + w i - 2 ,j + w i,j - 2 )) • Граничные условия дают равенства:

w0,j = wmj = 0, w2,j = 2w 1 ,j , wm-2,j = 2wm-1 ,j = 0, 0 < j < П, wi,0 = wi,n = 0, wi,2 = 2wi, 1, wi,n-2 = 2wi,n-1 = 0, 0 < i < m.

При конечномерной аппроксимации уравнение (5) превращается в уравнение

( A1W1 = q — r, A2 W2 = r, где A1 , A2 – симметричные, положительно определенные матрицы, а W1 ,W2 G Rmxn. Обратным операторам G1 , G2 также соответствуют некоторые матрицы G1, G2. В этом случае решение задачи (9) существует, и метод последовательных приближений (12) – (13), где операторы G1 и G2 нужно заменить на «сеточные» операторы G1 и G2 , сходится к некоторой точке r* G Rmxn . Метод (9) применялся для решения контактной задачи двух прямоугольных пластин и в нелинейном случае.

Если рассматривать нелинейные уравнения равновесия пластин в рамках теории Кармана, то вместо уравнения (5) необходимо решать систему уравнений:

D 1 ДД w 1 = q + ea ( w 1 , ф 1 ) — r,

— ДД ф 1 = —a ( w 1 ,w 2 ) ,

E

D 2 ДД w 2 = ea ( w 2 , ф 2 ) + r,

— ДД ф 2 = —a ( w 2 ,w 2 ) ,

E

где

∂ ² w ∂ ² ϕ   ∂ ² w

^{a ( w,ф} ) = dx 2 • lv ⁺ dy 2 •

∂2ϕ∂

—-— — 2 —7—

∂x2

∂ ² ϕ ∂x∂y

• - билинейная форма Кармана. При в = 0 уравнения (15) – (16) переходят в уравнения (7).

Функции напряжений ф ( x,y ) в самом простом случае граничных условий – отсутствие касательных и нормальных напряжений на краях пластины – удовлетворяют краевым условиям:

д ² ф i (0 ,у ) = д ² ф i ( a,у )

∂y ²          ∂y ²

д2 фi (0 ,у) = д2 фi (а,у) ∂x∂y ∂x∂y д2фi(х, 0) _ д2фi(x,b) _ дх2   =   дх2   = 0

д ² ф i ( х, 0) = д ² ф i ( x,b ) ∂x∂y ∂x∂y

= 0 , ( х,у ) G [0 ,а ] х [0 , b ] •

Для конечномерной аппроксимации уравнений (15) – (16) также применялся метод сеток.

Полученные результаты

Для пластин размером a = b = 40 см, h =

0 , 5 см, D 1 = D ₂ = 57 , 234 кг * см, D 1 = D ₂ =

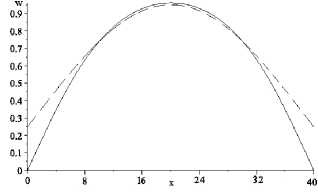
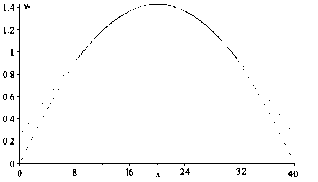
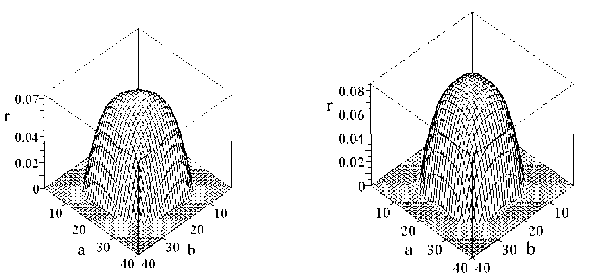
12Ehv2), v = 0, 3, модуль Юнга E = 5000кг/см2, нормальная нагрузка q = 0, 1кг/см2, с количеством точек разбиения m = n = 40, на рис. 1 показаны графики прогибов пластин w 1 (x, b/2), w2(x, b/2), где вдоль оси X указано изменение размера пластины при x e [0 .. .a ] в линейном и нелинейном случа- ях. На рис. 2 изображены реакции контактного взаи-

модействия между пластинами. По осям X и Y показаны размеры пластин a = b = 40 .

(a)

(b)

Рис. 1. Прогибы пластин w i ( x,y ) , i = 1; 2. Нелинейная теория Кармана (а), линейная теория (b).

Fig. 1. Deflections of the plates w i ( x,y ) , i = 1;2. Karman’s nonlinear theory (а), linear theory (b).

(a)                               (b)

Рис. 2. Реакция пластин r . Нелинейная теория Кармана (a), линейная теория (b).

Fig. 2. Reaction of the plates r . Karman’s nonlinear theory (а), linear theory (b).

Заключение

Рассмотрена контактная задача для системы двух параллельных пластин в линейной и нелинейной постановке. Проведено сравнение полученных результатов, которое показало, что учет «Карма-новских» добавок существенно влияет на величину контактного взаимодействия. Метод, применяемый в работе, основан на теории двойственности выпуклых задач оптимизации и может быть использован для широкого класса задач с негладкой нелинейностью, в частности, для решения контактных задач с неизвестной областью активного взаимодействия элементов. Его применение предполагает предвари- тельное обращение операторов уравнений равновесия контактирующих элементов. Решение уравнений механики стержней, пластин и оболочек само по себе представляет достаточно сложную проблему. Однако для этого можно использовать все классические методы (метод сеток, конечных элементов, граничных элементов и т.д.).