Нелинейные искажения группового сигнала в радиосистеме абонентского доступа

Групповой сигнал радиосистемы абонентского доступа DS-CDMA, представляющий собой амп-литудно-модулированную последовательность – сумму дискретных элементов (чипов) канальных переносчиков (например, функций Уолша) [1], обычно подвергается усилению на передаче и на приеме. Важным фактором, ухудшающим реальную помехоустойчивость системы, является нелинейность амплитудной характеристики (АХ) тракта, обычно включающего в себя усилитель мощности на передаче, последетекторный усилитель, демультиплексор на приеме и, возможно, другие устройства. Ниже анализируется процесс прохождения группового сигнала DS-CDMA через нелинейное устройство (НУ) с амплитудной характеристикой у(х), имитирующей результирующую АХ группового тракта.

Модель формируемого сигнала

В общем случае на входе НУ действует смесь х = м + е полезного сигнала и и шума £ (рис. 1). Собственный шум и частотные искажения в НУ учитывать не будем. На рис. 2 представлена дифференциальная функция биномиального распределения полезного входного сигнала НУ

^ (¹¹) = Е ^Р {¹¹ = ¹¹'•} ⁸ (¹¹ ""  ¹¹ i ) =

£+м £+г/        ^_м

= E^Ci² У ² О^-^)^ S(m-z/J

где ⁸(") – дельта-функция; L – количество канальных переносчиков – функций Уолша; Р^и = и^ – вероятность того, что амплитуда чипа и принимает значение u_l=i = -L,-L + 2,..,L; q – вероятность появления информационного (модулирующего) символа 1 (предполагается, что эта вероятность одинакова в каждом из L каналов).

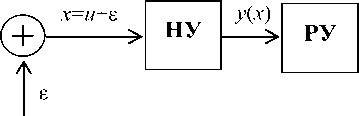
Рис. 1. Упрощенная модель группового тракта (НУ – нелинейное устройство, РУ – решающее устройство)

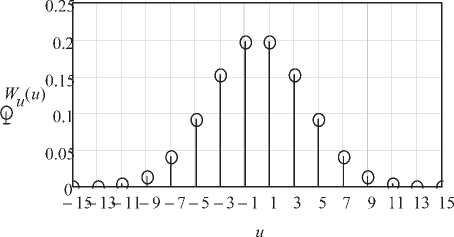
Рис. 2. Дифференциальная функция распределения полезного входного сигнала при L = 15, q = 0,5

Модель нелинейности

В основу анализа положим аппроксимационную модель реальной нелинейной АХ, предложенную в [2]:

Я*) =-------—

< гА2,,12р

1+ -v5)

где S – порог ограничения, р > 1 – целочисленный параметр, определяющий степень нелинейности АХ. Функция, обратная АХ, есть

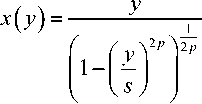
В частном случае отсутствия шума, то есть при в(/) = О (это допущение приемлемо для

НУ передающей стороны) X = U, y^Z/J = У^xj , m(j) = х(у). Семейства АХ и обратных функций при е(?) = 0, s = 15 , р = 1; 2; 10; 100, и₍ = Xj = —L, — £ + 2, — L + 4,.., L показаны на рис. 3 и рис. 4 соответственно.

My) ₌     1

dv 2^z(vMy)

Здесь для сокращения записи введена вспомогательная функция

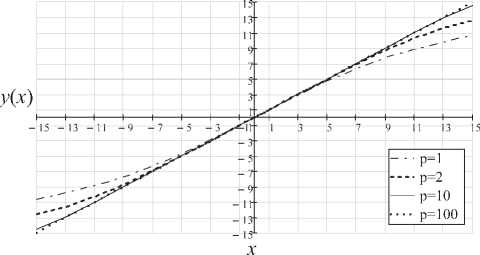
Рис. 3. Амплитудные характеристики НУ

^) = 1- f

2p

Тогда условная функция плотности выходной смеси

^„(.Vk)

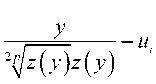
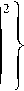
2^(,y)z(,v)V2no

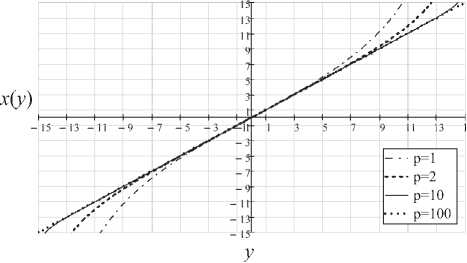
Рис. 4. Обратные амплитудные характеристики НУ

Графики ^(Ф/) для значений и, = —15; -1; 1; 15 при <7 = 1 представлены на рис. 5, а соответствующие графики ^v(y\«,) при p = 10 – на рис. 6.

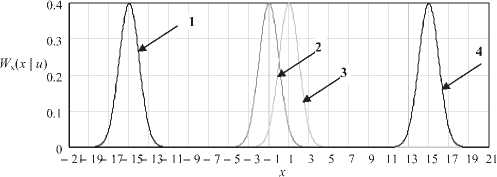
Рис. 5. Условные плотности распределения смеси сигнала с шумом на входе НУ (кривая 1: u = –15; кр. 2: u = –1; кр. 3: u = 1; кр. 4: u = 15)

Анализ искажений

Теперь учтем, что к полезному сигналу на входе НУ добавляется аддитивный гауссовский шум с нулевым средним и дисперсией о , плотность распределения которого

1 f E2 "'■(e)^exV^J'

В этом случае условная функция плотности входной смеси X = E + U_; сигнала с шумом (условие состоит в появлении сигнала Uj на входе НУ)

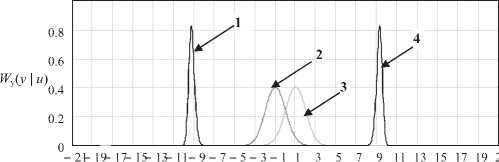
Рис. 6. Условные плотности распределения смеси сигнала с шумом на выходе НУ ( кривая 1: и = -15 ; кр. 2: и = -1; кр. 3: Ъ1 = 1 ; кр. 4: и = 1)

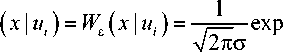
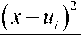
2cT

а условная функция плотности выходной смеси y согласно [3]

^(v|4.) = ^E[^(j)l4]

dy

Для отыскания безусловной (средней по всем значениям входного сигнала) плотности распределения смеси сигнала с шумом на выходе НУ найдем сначала, через свертку функций (1) и (3), безусловную плотность распределения суммы X полезного сигнала и с шумом Е на входе НУ:

где обратная функция х( у) найдена ранее (2). Производная обратной функции

1F_t(x) = j^, (u)^ (x -u^du -

A+w La-ti         ^__u

8(z/- u^C_L² q ² (1-g) 2

■sJIkg

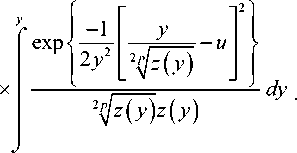
График W_x (x) представлен на рис. 7.

Для отыскания интеграла применим искусст

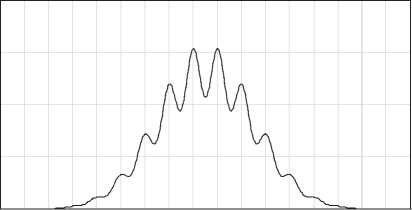
Рис. 7. Безусловная плотность распределения смеси сигнала с шумом на входе НУ

венный прием. Обозначим —, ^   = /. Тогда, dt 1

как можно показать, что   —- = —,    ----.

dv 2^z(y^

Заменяя переменную у на t, получим

Переходя к выходному сигналу y и учитывая (2) и (4)-(5), получим безусловную плотность распределения смеси сигнала с шумом на выходе НУ

Графики IF,. (.^V) при p =1; 10 представлены на рис. 8.

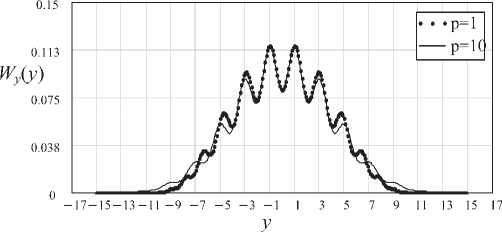
Рис. 8. Безусловная плотность распределения смеси сигнала с шумом на выходе НУ

Интегральная функция распределения смеси сигнала с шумом на выходе НУ согласно (6) равна

Lati Lau         £_u

^Н^И-Х^^^

Таким образом, выражение для интегральной функции распределения смеси выходного сигнала НУ с шумом приводится к табулированному интегралу. График ^Vy^ при o = i, р = 10 , £ = 15 показан на рис. 9.

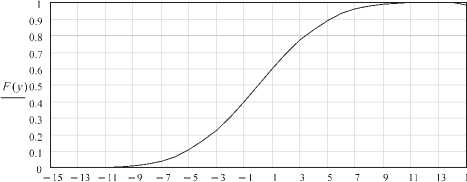
Рис. 9. Интегральная функция распределения смеси сигнала с шумом на выходе НУ

Поскольку функции V²V^Cyj и V^z(-^v) при У = ±5 терпят разрывы, при вычислении F(y) следует ограничиваться пределами — s-\-aгде а > О – достаточно малая величина, практически не влияющая на точность технических расчетов.

Заключение

Исследована модель группового тракта системы передачи информации с непосредственным расширением спектра и кодовым разделением каналов, учитывающая нелинейность амплитудной характеристики тракта. Показаны универсальность и удобство использования рассмотренной аппроксимационной модели для аналитических исследований. Результаты анализа иллюстрируются графиками, построенными с помощью программы Mathcad, и могут быть использованы для расчета реальной помехоустойчивости и задания технических требований к групповым трактам систем DS-CDMA.