Нелинейные колебательные процессы в динамике гусеничного движителя с резинометаллическими шарнирными соединениями

• -    вывод резонансных режимов за пределы рабочих частот путем изменения параметров динамической системы;

• -    применение гасителей резонансных колебаний (демпферов).

Введение в силовую схему резиновых вязкоупругих элементов существенно изменяет характер колебательных процессов, что необходимо учитывать при моделировании динамического поведения гусеничного движителя.

Целью настоящей работы является исследование влияния нелинейности жесткостных характеристик резинометаллических соединений траков на динамическое поведение гусеничного движителя. В связи с этим необходимо решить следующие задачи: создание математической модели динамического поведения элементов гусеничной цепи с учетом нелинейности жесткостных характеристик, создание алгоритма расчета для последующего проведения численных экспериментов с исследуемой математической моделью, анализ и обобщение результатов расчета.

В гусеничных движителях звенчатого типа наибольшее распространение нашли шарнирные соединения следующих типов: в виде простого металлического шарнира, резинометаллического шарнира и резинометаллического шарнира с ограничителями радиальной деформации. С учетом конструктивных, технологических и экономических факторов самым простым является соединение металлическим шарниром. Однако такой вид соединения обладает низким ресурсом вследствие интенсивного абразивного износа. Это приводит к постепенному увеличению зазоров в шарнирном соединении и вытягиванию гусеничного обвода. За счет этого увеличивается шаг гусеницы, нарушается контакта звеньев гусеничного обвода в зоне зацепления с ведущим колесом. Внедрение в шарнирное соединение траков резиновых элементов позволяет снизить динамическую нагруженность движителя за счет вязкоупругих свойств резины. Оптимальная комбинация резиновых и металлических элементов, а также рациональный выбор их параметров позволяют получить необходимые для снижения динамических нагрузок характеристики жесткости .

Однако проектирование и расчет технических конструкций, содержащих резиновые элементы, является достаточно сложной инженерной задачей. Связано это с тем, что резина как конструкционный материал обладает вязкоупругими характеристиками в большинстве своем нелинейного характера. Использование методов расчета на основе простых математических моделей не всегда дает адекватные результаты.

В работе [1] приводятся жесткостные характеристики различных типов шарниров, полученных в результате экспериментальных исследований. На рис. 1 - 2 приведены жесткостные характеристики соединений звеньев с металлическим пальцем (1М) и трех вариантов резино-

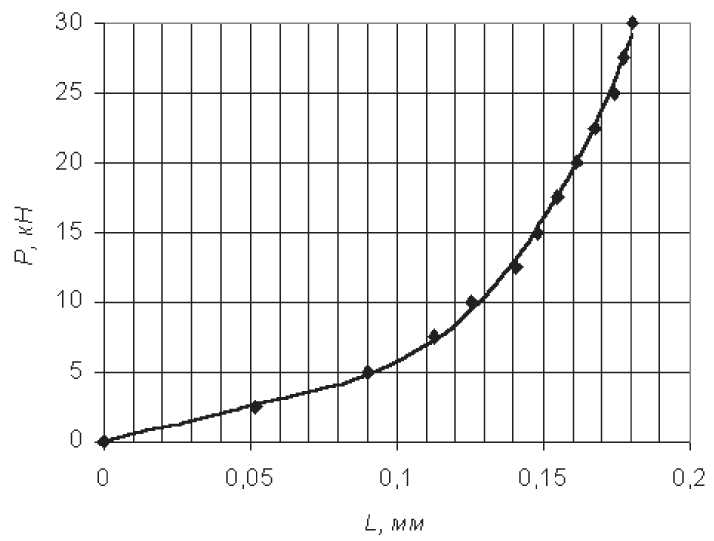
Рис. 1. Жесткостная характеристика металлического шарнирного соединения

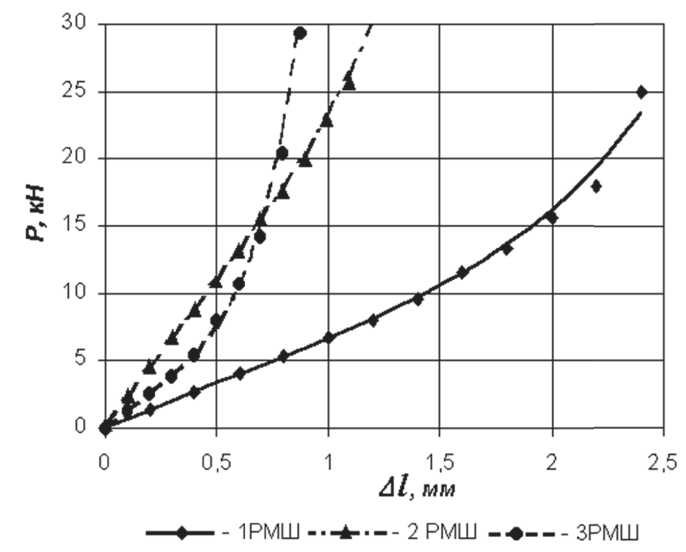
Рис. 2. Жесткостные характеристики резинометаллических шарнирных соединений

металлических шарнирных соединений (1РМШ, 2РМШ и 3РМШ).

Анализируя графики жесткостных параметров можно выделить следующие характерные участ- ки: на начальном этапе растяжения в шарнирах выбираются зазоры (линейный участок в начале графика), затем наблюдается значительный рост жесткости шарнира (прогиб пальца звена).

Математическая модель исследуемого участка гусеничной цепи представляет собой линейную многомассовую систему, элементы которой последовательно соединены вязкоупругими связями с коэффициентами жесткости к и демпфирования c . Динамическое поведение системы моделируется системой дифференциальных уравнений [2,3,4], для численного решения которой используется метод конечных элементов с дискретизацией по времени [5]. На каждом шаге реализации алгоритма расчета вычисляются динамические перемещения и скорости элементов системы, а также динамические нагрузки, действующие на резиновые элементы шарнирных соединений.

Работоспособность предложенного алгоритма проверялась сравнением результатов результатов теоретических и экспериментальных исследований свободных колебаний участка гусеничного обвода. В работе [6] приводится описание схемы экспериментального определения параметров свободных колебаний участка гусеничной цепи. На рис. 3 показана исследуе- мая система, которая содержит девять траков и девять шарнирных соединений. Кроме того на схеме показано расположение датчиков измерения динамических усилий в шарнирных со-

Для реализации алгоритма численного исследования приведенной схемы необходимо учесть нелинейность жесткостных характеристик. Коэффициенты жесткости представляют собой не постоянные значения, а вычисляются на каждом шаге алгоритма по формулам, аппроксимирующим экспериментальные данные. Наиболее точное приближение дает выражение вида

Р(х) = kx + k 2 x⁵ . (1)

В таблице 1 приводятся значения коэффициентов полинома для вычичления радиальной жесткости шарниров четырех типов.

На рис. 4 приводится сопоставление результатов экспериментальных и численных исследований процесса свободных колебаний гусеничной ветви для шарнирного соединения типа 2РМШ (Таблица 2).

Анализ графиков изменения растягивающих усилий в шарнирных соединениях показывает хорошее согласование результатов экспериментальных и теоретических исследований. Разность максимальных амплитуд составляет 4-6%. Некоторое различие в протекании колебательных процессов объясняется тем, что в работе [6] приведены сглаженные графики, не отражающие нелинейные процессы.

Проведение следующего этапа расчетов было связано с оценкой влияния нелинейности жесткостной характеристики шарнирного соединения на динамическое поведение элементов. На рис. 5 приведены графики амплитудно-частотных характеристик (4 шарнир) для различных вариантов расчета при внешнем синусоидальном нагружении с изменением частоты воздействия в диапазоне 50-70 с-1.

Анализируя приведенные расчетные дан- единениях.

ные можно сделать следующие выводы:

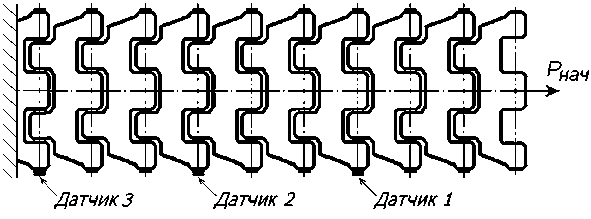
Рис. 3. Схема экспериментального определения параметров свободных колебаний ветви гусеничной цепи

Таблица 1. Значения коэффициентов полинома для расчета жесткости шарнира

Тип шарнира	Величина зазора, мм	k i , Н/м	к- 2 1 , Н/м5
1М	---	4,774x10 7	1,017x1023
1РМШ	0,625	6,545x10 6	9,699x1016
2РМШ	0,590	1,985x10 7	1,510x1018
3РМШ	0,462	1,180x10 7	3,397x1019

Таблица 2.

	Параметр	Размерность	Значение
1	Число временных конечных элементов	-	3000
2	Величина конечного элемента Tau	с	10-4
3	Масса звена m	кг	15
4	Начальное растягивающее усилие Рнач	кН	30
5	Коэффициент демпфирования c	кН*сек/м	0,85
Коэффициенты нелинейной жесткостной характеристики шарнира:
6	k 1	кН/м	1,985x10 7
7	k 2	кН/м5	1,510х1018

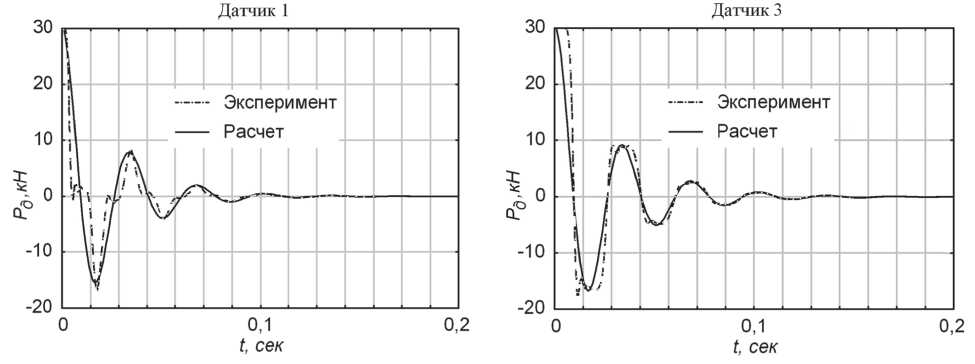
Рис. 4. Значения динамических нагрузок в шарнирных соединениях при свободных колебаниях участка гусеничной цепи

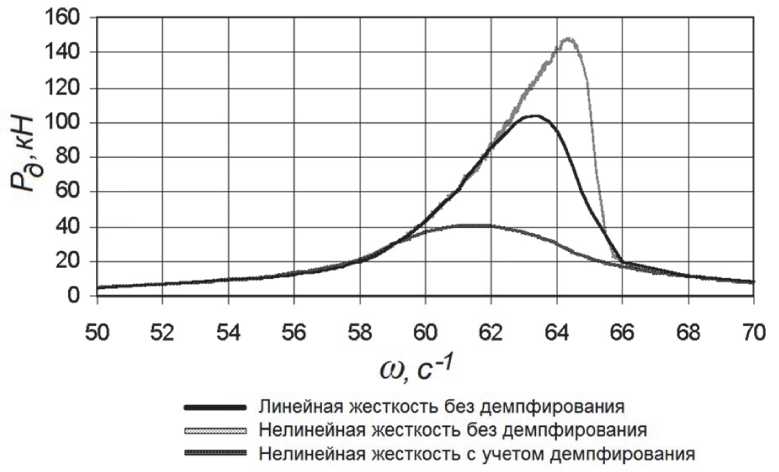
Рис. 5. Амплитудно-частотные характеристики

• -    с учетом нелинейности жесткостной характеристики резиновых элементов наблюдается смещение пика резонанса в сторону увеличения частоты внешнего воздействия;

• -    расчеты, проведенные с учетом демпфирования, выявили значительное снижение динамических нагрузок, возникающих в резиновых элементах шарнирного соединения траков.

Таким образом, показано, что нелинейность жесткостной характеристики резиновых элементов шарнирного соединения звеньев гусеничной цепи оказывает существенное влияние на картину динамической нагруженности. Этот аспект необходимо учитывать при моделировании динамических процессов, происходящих при движении гусеничного транспортного средства.