Нелинейные модели взаимосвязи распространения Inonotus obliquus (Pers.) Pil. с бонитетом и возрастом березового леса. Влияние ряда морфологических характеристик насаждений на встречаемость базидиального макромицета

Эксперимент ставился на безразмерных пробных площадях с 1000 экземпляров деревьев на каждой. Как правило, на одну градацию параметра таксации по две пробы размещались в Вешкаймском и Ульяновском лесничествах, 3 – Барышском. На всех безразмерных пробных площадях производился сплошной пересчет деревьев с подразделением их на здоровые и пораженные. Установление степени влияния таксационных показателей на степень распространенности I. obliquus осуществлялось в весенне-летний период. Кратность воспроизведения испытаний составляла семь раз, т.е. на каждой пробе учету подлежало 7 тыс. штук березы повислой. Таксация насаждений опиралась на глазомерный и глазомерно-измерительный способы, обеспечивающие закрепленную Лесоустроительной инструкцией 2008 г. нормативную точность определения таксационных признаков лесов [1, 4]. Пробные площади закладывались с соблюдением ОСТ 56-6983 «Пробные площади лесоустроительные. Метод закладки» [7]. Для бонитировки лесонасаждений использовалась шкала классов бонитета, предложенная в 1911 году профессором М.М. Орловым [9, 10]. Класс бонитета устанавливался по средним возрасту и высоте основного элемента леса. Также обеспечивалась увязка классов бонитета с типами леса, типами условий местопроизрастания. Возраст древостоя рассчитывался как средневзвешенная величина пропорционально представительству сумм площадей поперечных сечений отдельных совокупностей деревьев в их общей сумме [11].

Статистическая обработка данных основывалась на библиографических руководствах по теории вероятностей [2, 3, 5, 8, 12]. Вводилась поправка Бонферрони. Дисперсионный анализ проводился методом однофакторных комплексов. В работе осуществлялся и корреляционно-регрессионный анализ.

Эмпирический корреляционный коэффициент рассчитывался по формуле n

J Я ( x i - x ) 2 Я y - y ) 2 ; случайная ошибка оценки его генерального пара

r xy = Я ⁽ x i - x ⁾⁽ y i - ^y )

i = 1

метра р: sr =д/(1 — r2)/(n - 2); критерий проверки нулевой гипотезы при числе степеней свободы k = n - 2 - согласно аналитическому неравенству tнабл = r7(n - 2)/(1 - r2) > tкр. Линейная зависи мость переменных Y и X описывалась уравнением общего вида yx = a + bx 1 + cx2 + dx3 +..., где a, b , c , d , … – параметры уравнения, показывающие соотношения между аргументами x1 , x2 , x3 , …, xm и функцией yx . Коэффициент регрессии b вычислялся как: byx =(n Я xy -Яx Я y У(п Яx 2 -(Я x)2); коэффициент сдвига a - ayx = (ЯyЯx2 -ЯxЯyx)/(nЯx2 - (Яx)2)’ ошибка выборочного коэффи- ixi - x )2), а ее достовер

циента регрессии Y по X – по формуле s byx ность - по t-критерию Стьюдента tнабл = b / sb. Для проверки значимости полученной формализации, т.е. адекватности результатам эксперимента, употреблялся критерий Фишера Fнабл = sj /sj , теоретическое обоснование которого отводилось по таблице Фишера Fkp (a, n -1, n - 2). Регрессия признавалась адекватной опытным данным при F.-, > F .

набл кр

Результаты и их обсуждение. Полученные результаты по распространенности I. obliquus в березняках, разнящихся по таксационным параметрам, отображены в таблице.

Встречаемость I. obliquus в зависимости от морфологических характеристик березовых древостоев, шт/1 тыс. деревьев

Классы бонитета	Ia	I	II	III	V	Среднее
X±Sx	0,14±0,14	0,14±0,14	0,29±0,18	0,29±0,29	0,43±0,20	0,26±0,09
Классы возраста	IV	V	VI	VII	VIII	Среднее
X±Sx	0,14±0,14	0,14±0,14	0,29±0,29	0,43±0,20	0,71±0,36	0,34±0,11
Стадии рекреационной дигрессии	1	2	3	4		Среднее
X±Sx	0,14±0,14	0,14±0,14	0,29±0,29	0,57±0,20		0,29±0,10
Полнота	0,6	0,7	0,8	0,9		Среднее
X±Sx	0,43±0,30	0,14±0,14	0,29±0,18	0,00±0,00		0,21±0,09
Породный состав	6С4Б	6Б4С	8Б2С	10Б		Среднее
X±Sx	0,00±0,00	0,14±0,14	0,29±0,29	0,43±0,20		0,21±0,09
Тип леса	Б брзм	Б орл	Б мтр	Б сняс		Среднее
X±Sx	0,43±0,43	0,14±0,14	0,14±0,14	0,29±0,18		0,25±0,12

Судя по данным, содержащимся в таблице, в целом на степень встречаемости трутового гриба в березовых лесах региона с разной силой оказывают влияние их таксационные признаки. Причем воздействие отдельных экологических факторов, выражаемых параметрами лесотаксации, на насаждения в случае с каждой группой выборок носит особый характер, о чем свидетельствуют математические ожидания последних, далеко не всегда присутствующая монотонность динамики распространенности I. obliquus по мере постепенного изменения таксационного показателя, ошибки внутригрупповых совокупностей и проч. Так, если при повышении доли участия березы в общей формуле состава древостоя встречаемость макромицета прогрессивно увеличивается и обладает, скорее всего, очень близкой к линейной положительной формой зависимости от видового состава, то, например, с возрастанием полноты леса она скачкообразно уменьшается. То есть, во втором случае помимо колебательного движения мы наблюдаем еще и обратную отрицательную зависимость между рассматриваемыми показателями, хотя безусловно следует принимать во внимание специфику действия конкретного фактора, особенности формирования обозначений того или иного таксационного параметра. В более высокопроизводительных типах леса (березняки: мелкотравный – Б мтр и орля-ковый – Б орл) гриб менее распространен, нежели в низкопродуктивных (снытево-ясменниковый – Б сняс и бруснично-зеленомошный – Б брзм березняки). На данный факт указывают и результаты эксперимента по изучению частоты встречаемости I. obliquus в березовых древостоях с различным бонитетом условий местопроизрастания: с повышением бонитета (от V к Ia классу) базидиомицет реже обнаруживается. При увеличении степени рекреационной деградации насаждений распространенность I. obliquus не падает, а, наоборот, повышается. Однако в ряде испытаний частота встречаемости гриба на некотором отрезке градации таксационного признака сохраняется, что, по-видимому, объясняется как случайными причинами, так и объективными – достаточно близкими их характеристиками. Например, в Б мтр и Б орл распространение возбудителя гнилевого заболевания составляет порядка 0,14±0,14 шт/1000 экземпляров деревьев, даже одинаковые значения ошибки. Встречаемость патогена в насаждениях с 1-й и 2-й стадиями рекреационной дигрессии располагает также около 0,14±0,14 шт/1000 экземпляров деревьев. В последнем случае объяснением подобного, вероятнее всего, служат характеристики означенных двух стадий, обладающих довольно большим сходством. Кроме того, с 3-й стадии дигрессии (предел устойчивости лесного биогеоценоза) начинаются необратимые изменения в жизни леса.

Далее мы подробнее остановимся на оценке влияния классов бонитета и возраста древостоя на численность популяции трутовика скошенного с целью последующего осуществления соответствующего корреляционно-регрессионного анализа и построения моделей.

Как видно из таблицы, для анализа нами не был организован IV класс бонитета, поскольку площадь лесных массивов с ним в итоге не превысила и 0,23% от общей площади березовых насаждений, произрастающих на территории трех лесничеств региона. Как уже отмечалось, встречаемость I. obliquus несколько возрастает с повышением класса бонитета (предположительно прямая линейная зависимость). Вероятно, подобное прежде всего связано со спецификой проявления иммунологических свойств березы, зависящей от условий окружающей среды. Достаточно вспомнить, что степень добротности условий местопроизрастания влияет на активность протекания ряда физиологических процессов у растений, обусловливающих в конечном счете направление их врожденного иммунитета. Активная иммунность в отношении возбудителя в свою очередь усиливается с увеличением интенсивности осуществления биохимических реакций древесным растением в связи с более благоприятными факторами внешней среды.

Однофакторный комплекс, слагаемый эффектом численности факультативного ксилотрофа и фактором бонитета (пять типов), оказывающим непосредственное влияние на конечный результат, мы разложим на составляющие вариации согласно элементам системы дисперсионных оценок по Фишеру-Снедекору. Таким образом, градация дисперсий приобретет вид: факториальная – 0,4, внутрисовокупностная (дисперсия остаточной последовательности) – 8,29 и интегральная компонента – 8,69. F _ф =0,36 не превышает F _st =2,69 (0,05, 4, 30), что сохраняет в силе нулевое предположение: эффективность действия фактора на результат X (встречаемость патогена) в нашем случае статистически незначима. Тем не менее условие F_ф ≥ F_st выполнимо при P≥0,83. По k_{д . факт} =4,61%, распространение I. obliquus в березняках приблизительно на 0,05 (1/20) подчиняется бонитету леса.

Корреляционно-регрессионный анализ вначале проведем по линейному алгоритму методом наименьших квадратов на регрессор класса бонитета и отклик – частоту встречаемости I. obliquus .

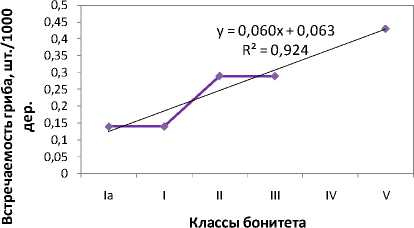
В постулируемом уравнении линейной регрессии можно допустить наличие прямой сильной взаимосвязи класса бонитета условий местопроизрастания березы и численности популяции скошенного трутовика, так как корреляционный коэффициент r=0,96. Согласно t-критерию t_набл =6,05, превышающему t_кр =3,18 (0,05, 3), оценка достоверности коэффициента корреляции и значимости коэффициентов регрессии a и b положительна. Уравнение прямой взаимосвязи между объясняемой переменной Y (миграцией I. obliquus в насаждениях) и объясняющей переменной X (их классом бонитета) показано на рисунке 1.

Линейная

0,5

0,45

0,4

0,35

0,3

0,25

0,2

0,15

0,1

0,05 0

Логарифмическая Экспоненциальная

a го ю

s

0,5

0,45

0,4

0,35

0,3

0,25

0,2

0,15

0,1

0,05 0

y = 0,000x2 + 0,058x + 0,066 R² = 0,924

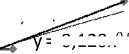
= 0,120x0,668 R² = 0,849

0,5

0,45

0,4

0,35

0,3

0,25

0,2

0,15

0,1

0,05 0

y = -0,002x3+ 0,022x2 - 0,007x + 0,117 R² = 0,927

y = 0,014x4-0,199x3+ 0,897x2 - 1,520x + 0,

Ia I II III IV

V

Классы бонитета

Ia I II III IV

Классы бонитета

V

Параболическая Степенная

Полиномиальные с k=4 Кубическая парабола

Рис. 1. Регрессии зависимости распространения I. obliquus от класса бонитета леса

Коэффициент детерминации R ² =0,92 линейной формализации указывает на достаточно высокое качество построенной модели – регрессионным уравнением не учитывается лишь менее 8% фактора.

Заключение о достоверности всего однофакторного математического моделирования и величины ошибки аппроксимации позволяет сделать F-критерий, экспериментальное значение которого 36,59 превосходит как критическое 10,13 (0,05; 1; 3), так и табличное 34,1 (0,01; 1; 3).

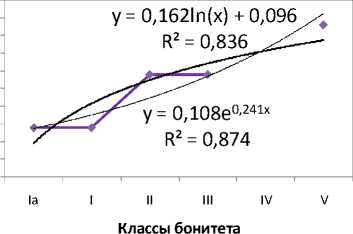
Около 100% регуляции влияния бонитета леса на численность популяции трутовика скошенного позволяет осуществить регрессия посредством полинома 4-й степени (рис. 1). Причем в предполагаемых обстоятельствах криволинейные модели, построенные по алгоритмам экспоненцирования и логарифмирования ( R ² =0,874 и 0,836 соответственно), а также возведения в степень ( R ² =0,849), по уровню прогноза даже не превосходят линейную модель зависимости ( R ² =0,924). В то же время начинают опережать последнюю по эвристичности лишь уравнения мультиномиальные, и параболическая 3-й степени – первая из их числа, хотя она и ненамного улучшает прогноз (92,4<92,7%).

Таким образом, парный корреляционно-регрессионный анализ все-таки позволил получить адекватные аналитические формы взаимосвязи между частотой обнаружения I. obliquus в насаждениях и их бонитетом.

Стоит рассмотреть и некоторые особенности влияния возраста березняков на встречаемость I. obliquus . Так, исходя из табличных данных (см. табл.), степень встречаемости ксилотрофа в древостоях постепенно увеличивается с повышением их класса возраста. В березовых древостоях IV и V классов возраста характер распространенности патогена схож. Данное обстоятельство не помешало в итоге предположить о присутствии линейной формы статистической зависимости между возрастом древостоя и частотой обнаружения I. obliquus . Мы считаем, что большая поражаемость макромицетом старших поколений питающего растения обусловливается прежде всего тем, что старые экземпляры березы более подвержены заражению грибами, поскольку с течением времени у них снижается способность образовывать раневое ядро, препятствующее проникновению спор внутрь древесины.

Посредством вариационного анализа, проводимого методом однофакторных комплексов и позволяющего осуществить оценку дисперсий, теперь проследим характер влияния качественного признака иного рода (возраста березовых насаждений) на прежний результирующий (X) – встречаемость факультативного сапротрофа. Как и в предыдущем случае, в рассматриваемом ортогональном статистическом комплексе 5 факторных уровней с количеством вариант 35.

Факторная дисперсия равна 1,6, случайная вариация – 12,29 и их общая сумма – 13,89. Причем дисперсионное отношение F _ф составило 0,98 и так же не превысило критической величины F _st =2,69 (0,05; 4; 30), а значит, нулевая гипотеза остается в силе. В конкретном примере условие F_ф ≥ F_st положительно разрешается при выполнении неравенства P≥0,43, в то время как ранее речь шла о P≥0,83. Следовательно, возраст березового леса в большей степени оказывает влияние на пространственную организацию патогена, чем бонитет насаждений. Последнее, по всей видимости, должно отразиться и на повышении коэффициента детерминации. Действительно, по k_{д . факт} =11,52% (прежде k_{д . факт} =4,61%, т. е. с разницей в 6,91%), эффективность определения встречаемости I. obliquus в березняках классом возраста древостоя в 2,5 раза превосходит результативность от класса бонитета.

По итогам полученного материала был проведен однофакторный корреляционно-регрессионный анализ с целью установления аналитической формы взаимосвязи между степенью распространенности I. obliquus в насаждениях и их возрастом. В этом случае объясняющей переменной X служил возраст древостоя с градацией в один класс, а отклик остался прежним – встречаемость патологического агента.

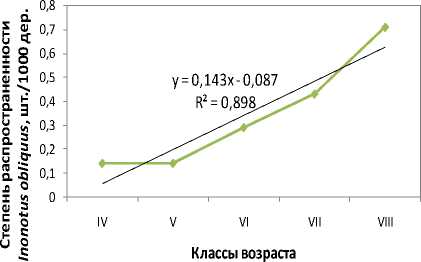
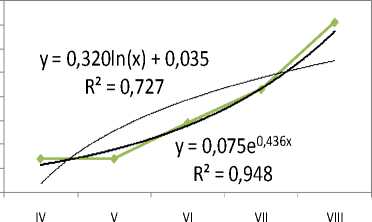
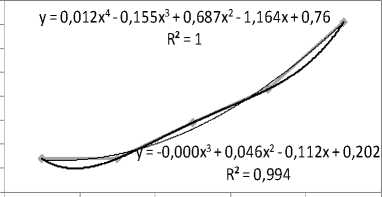
Линейный коэффициент корреляции r=0,95, что позволяет предполагать о наличии прямой сильной связи между классом возраста древостоя и распространением гриба (коэффициент близок к 1 и 0,75 ≤ r ≤ 1,00 [5]). Отношение эмпирического выборочного коэффициента корреляции к своей ошибке t_набл =6,67 превосходит t_кр =3,18 (0,05; 3). То есть r значим статистически, наблюдаемое линейное коррелирование двух явлений действительно, а гипотеза о нулевом наклоне прямой регрессии несостоятельна по тождеству с предположением об отсутствии корреляции вовсе [2]. На рисунке 2 показаны уравнения зависимости степени распространенности I. obliquus от класса возраста леса.

Линейная

s ь u О

Ф re Q. ь u О a c u re a.

ф c £ и

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

Классы возраста

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

0,8

y = 0,106x1,016 R² =

y = 0,039x2 - 0,092x + 0,188 R² = 0,993

IV              V             VI             VII            VIII

Классы возраста

0,7

0,6

0,5

0,4

0,3

0,2

0,1

Экспоненциальная Логарифмическая

IV              V              VI              VII             VIII

Классы возраста

Степенная Параболическая

Кубическая парабола Полиномиальные с k=4

Рис. 2. Регрессии частоты встречаемости I. obliquus на класс возраста

Проверка линейной модели по величине достоверности аппроксимации свидетельствует о довольно высоком качестве уравнения регрессионной функции (общая описательная составляющая около 90%). Вывод о достоверности меры определенности и всей построенной при ее обосновании модели допускает сделать F-критерий Фишера, опытное значение которого 26,68 оказалось больше критического 10,13 (0,05; 1; 3). Однако при α =0,01 положение об их значимости математически не подтверждается, поскольку в этом случае статистическая величина критерия Фишера 34,1 (0,01; 1; 3) уже превышает наблюдаемую.

Попытаться построить новую модель, которая по качеству превзошла бы предыдущую, при анализе данных статистик все же возможно, например, экспоненциальным аппроксимированием (см. рис. 2) зависимости встречаемости I. obliquus в насаждениях от их класса возраста. Так, моделирование уравнения с применением экспоненты позволит на 5% вдобавок к ранее разработанному равенству (по R ² , 95 против 90%) повысить вероятность прогноза динамики численности возбудителя по возрасту березовых лесов.

Сравнивая в общем и целом нелинейные формализации взаимосвязи степени распространенности чаги и двух таксационных показателей древостоев, классов бонитета и возраста по отдельности, выстроенные по аналогичным криволинейным регрессионным алгоритмам, можно отметить, что в случае с оценкой воздействия бонитета березовых насаждений на частоту встречаемости трутового гриба мера определенности каждой из них составляет: экспоненциальной – 87,4%, логарифмической – 83,6, параболической – 92,4, степенной – 84,9, полиномиальной 3-й степени – 92,7 и полиномиальных всех последующих порядков – 100%. При анализе же влияния возраста березовых насаждений на характер распространения I. obliquus экспоненциальная аппроксимация определялась 94,8% детерминацией фактором популяционной численности патогена, логарифмическая – 72,7%, параболическая – 99,3, степенная – 83, многочленная путем кубической параболы – 99,4, а полиномиальные с k≥4 – сходной с бонитетом, т.е. 100% (см. рис. 2). Как мы наблюдаем, логарифмические и степенные регрессии в этих двух статистических рядах по эвристичности уступают прямолинейным. В плане прогноза встречаемости ксилотрофа уступает линейной еще и экспоненциальная регрессия на класс бонитета, однако последняя при описании влияния фактора возраста березняков на распространенность в них I. obliquus – одна из самых наиболее прогностичных и правдоподобных. Многочленные уравнения 2, 3 и т.д. степени во втором случае относительно аналогичных нелинейных моделей для установления степени поражаемости I. obliquus лесонасаждений по бонитету в предсказаниях динамики численности возбудителя по параметру таксации явно предпочтительнее. Хотя безусловно обращает на себя внимание факт отсутствия IV класса бонитета для организации анализа воздействия фактора бонитета березовых насаждений на степень распространенности трутовика скошенного в настоящей работе, о причине которого сообщалось выше.

Выводы

• 1.    На степень распространенности I. obliquus в березовых лесах оказывают влияние биоэкологические факторы. Встречаемость гриба в целом увеличивается по мере повышения доли участия березы в общей формуле состава древостоя, класса возраста, стадии рекреационной деградации насаждений. Но уменьшается с повышением полноты и бонитета древостоя (от V к Ia классу). В более высокопроизводительных типах леса макромицет менее распространен, чем, соответственно, в низкопродуктивных.

• 2.    Характер встречаемости трутового гриба по-разному обусловливается отдельными морфологическими характеристиками лесонасаждений. Например, возраст древостоя в 2,5 раза сильнее определяет численность популяции I. obliquus , нежели его бонитет.

• 3.    Наибольшим качеством прогноза поражаемости факультативным сапротрофом березняков, причем как по бонитету, так и их возрасту, обладают модели, построенные по алгоритмам полиномиального аппроксимирования 4-го и выше порядка, достаточным – также и линейные регрессионные формализации.

Полученные результаты призваны ориентировать лесохозяйственное производство на создание новых и регуляцию уже существующих березовых насаждений разреза рассмотренных показателей таксации в соответствии с критерием минимальной численности популяции трутовика скошенного. Что, в свою очередь, скажется и на результирующем эффекте основных функций, как общепланетарных, так и локальных, выполняемых березовыми лесами. Экспериментальные данные также показывают на неоднородность влияния различных экологических факторов на пространственную организацию ксилотрофа, позволяющую в отношении отдельных таксационных параметров особо избирательно подходить к формированию структуры устойчивых насаждений. Для уменьшения вероятности возникновения эпифитотий вследствие I. obliquus рекомендуется:

• -    стремиться к созданию высокобонитетных березовых древостоев, поскольку условия местопроизрастания – ведущие факторы, определяющие взаимоотношения структурно-функциональных элементов любых экосистем леса и оказывающие заметное влияние на общее фитосанитарное состояние лесных биогеоценозов;

• -    содействовать образованию разновозрастных березняков, так как возрастная структура лесонасаждений имеет организующий характер, определяет глубину и направление фитопатологического воздействия на лесные комплексы планеты;

• -    своевременно назначать в рубку и выбирать спелые и перестойные насаждения, уже выработавшие свои основные функции;

• -    изымать пораженные I. obliquus деревья в ходе проведения периодических санитарных рубок и др.