Нелинейный изгиб консоли распределенной нагрузкой

Поведение и устойчивость тонкого гибкого стержня под воздействием распределенной нагрузки рассматривались в работах многих авторов, например в [1]. В этой работе приведены точные геометрически нелинейные уравнения равновесия упругого стержня при действии распределенной нагрузки, справедливые при больших упругих перемещениях изогнутого стержня в одной плоскости, аналитические решения уравнения равновесия и найдены общие выражения для изогнутых форм упругой линии в полярных координатах с помощью сложной комбинации эллиптических функций Вейерштрасса. Но там не рассматривалась краевая задача, учитывающая условия закрепления стержня.

В работах [2; 3] была развита геометрически нелинейная теория изгиба тонких стержней. В них применялся статический критерий устойчивости стержней, исходя из уравнения равновесия типа нелинейного маятника. Это позволило найти точные аналитические решения задач изгиба стержня сосредоточенными силами - следящими и постоянного направления.

Ниже будет представлено точное аналитическое решение задачи об изгибе консольного стержня распределенной нормальной нагрузкой.

Уравнение равновесия стержня, изогнутого нормальной распределенной нагрузкой. Рассмотрим тонкий гибкий стержень длиныД к которому приложена распределенная нормальная нагрузка q (рис. 1). Будем искать формы изгиба стержня при постепенном увеличении внешней приложенной нагрузки.

Рис. 1. Система координат / -криволинейная координата точки стержня; (г, ф) - полярные координаты; с (/) - угол наклона касательной к оси OX; q - величина внешней приложенной нагрузки

Уравнения равновесия стержня запишем в виде:

dM      dF    dM      dF

= - F n , ^ = K л =- F n , 07 = K dl           dl       dl           dl

гдеМ- величина изгибающего момента; F - полная сила внутренних напряжений; K - внешняя распределенная нагрузка.

Переходя к касательной системе координат, запишем систему (1) в виде

d26- 17 dl2 n, (2а) dFт _ .de =n 11 Fn 11    0 , dl dl (2б) 17 d 6^ dF ft-+X = q, (2в) dl dl гдеКт = 0, К^ = q - касательная и нормальная компоненты распределенной нагрузки соответственно; F, Fn - компоненты внутренней силы

Переход между декартовой и касательной системой координат описывается системой

A _T = A x cos 6 + A y sin 6 ,

A = - A_v sin 6 + A cos 6 . nx   y

(3а)

(3б)

Пользуясь системой (3), найдем нормальную компоненту силы F , для чего запишем екартовы компоненты нормальной распределенной нагрузки в виде

К = -q sin с, К = q cos с. х                    У ¹

Тогда декартовы компоненты силы F будут

Fx = - J q sin 6 dl = - qy, Fx = - J q sin 6 dl = - qx.

Через декартовы компоненты силы F , согласно (3б), выразим нормальную компоненту

F_n = q У sin с + q х cos с.

Подставим полученное выражение в (2а) и найдем выражение для кривизны линии изогнутого стержня йс I d/:

„ d2 6

EI ddf = - q ( У sin 6 ⁺ x cos 6 ) .

Проинтегрируем его по d/:

d 6    q r2

=         + dl    EI 2 EI

Перейдем к безразмерной переменной t=/1L, переписав выражение для йи1 d/ в виде

1 d 6 qr ² C --= —- + — L dt    EI 2 EI .

Сделав замены констант и координат: X = (qL³IEI)¹¹³, г₁ = X г IL, и = X t, С₀ = CL I EI, получим следующее выражение для кривизны линии изогнутого стержня:

d ⁶ =- 1 ₊ C, .

du 2 X

Работа выполнена при поддержке гранта Президента РФ МК-5141.2006.1

Разместим стержень в начале координат таким образом, чтобы в точке и = 0 значение г₁ = 0:

и =

d6 (0) = C0 . du     1 (5) Пусть при этом производная dи / dи в 0 равна величине 2 к, тогда получим что точке С0 = 2к1, (6) d6 (0) = 2 k, du (6а) d6 = r12 + 2 k. (7) du 2

Преобразуем систему (2), используя (2а), и (26):

^d F ’ + B^{4 1}6 d ⁶ = 0 dl dl ² dl

I M = ¹ - k 3 - f + 2 k ‘ f 12 - k 2 ./ 1* .       (14)

I du j k k

Будем искать решение уравнения в виде дробно-линейной комбинации эллиптических функций Вейершт-

расса

= « 1 ₊Р 1 g ⁽ u ) , a 2 +р 2 g ( u )

dg I = 4 g ³ + bg + c , du 1

(15а)

(15б)

•

гдеg = Р (и, b, с) - эллиптическая функция Вейерштрасса, получаемая обращением нормальной формы Вейерштрасса эллиптического интеграла 1-го рода:

7 ds и = I I = s V4s3 + bs + c "

Найдем первый интеграл:

F + EI | d T C ..

^T 2 ( dl J ¹

Преобразуем равенство (8) с помощью (За),

.       . _ EI | d 61

- q y cos 6 + qx sin 6 +         = ц .

2 I dl J ¹

Пусть / = 0, тогда x =y = 0и

EI I d⁶ (0) ) = C •

здесь b, с - периоды функции Вейерштрасса.

Определяя коэффициенты в системе (15) при условии в ₁ Ф Р ₂ и при требовании, чтобы коэффициенты a_p a ₂, а , с были вещественными, получим следующие ограничение на к:

Перейдем к переменной и и с помощью (6а) следующее равенство

С

' = 2 k ² К ².

EI

Подставим (8) в (2в):

_ d 6 EI | d 0 | 3 __d ³6

C --       - EI —_г = q .

¹ dl 2 I dl I         dl ³

получим

Перейдем к переменной t и параметру л и сделаем замену/= de / dt Тогда выражение (10) примет вид

d f = - X³ + 2 k ² X ² f - ¹ f ³. dt ²                     2

Вид этого дифференциального уравнения совпадает с видом дифференциального уравнения, характерного для эллиптических функций [4]:

df = ^a + aj + 2 a J ³.

dt ² 2 ²⁴

Проинтегрируем уравнение (12а):

I dl                             2         4

I — = ^a 0 + ^a i ^f + ^a 2 f + ^a 4 ^f .

dt

(12а)

Определим коэффициенты системы (12), используя (11). Пусть при этом d/V dt = 0 и t =0, тогда а 0 = 4 k 14 (1 - k3), a1 = -2X3, a 2 = 2 k2 X2, a 4 = 4 •

Запишем (126) в виде

f ) = 41 ⁴ dt j

k (1 - k 3 ) - f + 2^ 2 1    4 1 ²

^^^^в

f ⁴

16 1 4 •^(1З)

Сделаем замену) =/ / 2к 1 , и перейдем к и;

Далее для простоты вида функции) положим р ₁ = в ₂ = 1, и, используя метод неопределенных коэффициентов, найдем a ₁, a ₂, b, с:

4k3-3 „ _k2 . _ 14k4 Ct, =----- a2 = — b = -     - k a     12k ’       3 ’ I 3

1 8 k ⁶ c =-

I 27

-

k ³1

+

3 16

Тогда выражения (15а)и(15б) будут: 4 k3 - 3, .

⁺ g ^{( u} )

г = 12 k, f1

у ⁺ g ⁽ u )

8 k ⁶

k

-

,

+

(18а)

Преобразуем (18а) к виду

fx = 1 -

4 k I k ² , Д’ I у ⁺ g ⁽ u )

откуда получим, ограничение области значения функции Л Фис.2):

/^1.

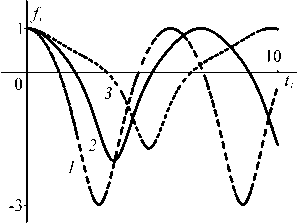
Рис. 2. Вид функции) при различных значениях к:

7 - к = 0,4, 2 - к = 0,7, 3 - к = 0,9

Преобразуем уравнение (14) к виду u = J . f            .        (20)

0/~~Г — f + 2 '2 f" — ' 2 fl kk

Функция угла наклона касательной к оси ОХс(Л описывается следующими равенствами:

dc(t)/dt = 2кл/!(11),(21а)

с(1)=2 k 1J fl (1t) dt.(21б)

Найдем полярные координаты точек изогнутой линии стержня. Для этого запишем уравнение равновесия малого элемента изогнутого тонкого стержня согласно [2]:

(1 / с) = dC/dZ = 4АР + 4В.(22)

Перейдем от переменной / к переменным и и г и сделаем замену A =   , B = BL :

13     1

d ⁶ = 4 Ar ² + 4 B. .

du      111

Сравним уравнение (23) с (7):

Л1 = 1/8, В1 = к/2.

Тогда (22) запишем в виде d6

du

- r - + 2 k .

После преобразований: с учетом (18а) и (21а), получим выражение для г:

- = I .(26)

1^ 3 + g ( t )

Найдем угол ц согласно формуле, приведенной в [2]:

— = A-2 + 2B.(27)

dl

Переходя к переменной t и, используя (24) и (26), получим выражение для угла ф :

ф = с/4 + ^1/2.(28)

Формулы (26) и (28) определяют формы прогиба стержня при приложении к нему внешней распределенной нормальной нагрузки q. Решения записаны в единой параметрической форме и зависят от параметра к, определяемого внешней приложенной нагрузкой q.

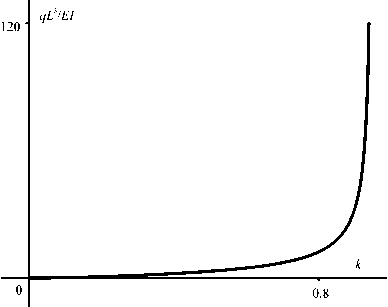
Рис. 3. Спектр собственных значений, связывающий между собой внешнюю приложенную нагрузку q и модуль эллиптических функций к (первая мода решения)

Учет граничных условий. Граничные условия для стержня запишем в виде

с(1 = 0) = 0 - защемление слева,(30а)

Ас / dt (t = 1) = 0 - свободный конец справа. (30б)

Полагая t = 1, из (7) получим и = 1 . Следовательно, уравнение (20) преобразуется к виду

(А q о =

г

0/--Г - f- + 2 k2

kk

Выражение (31) описывает зависимость q0(k) для первой моды решения (рис. 3).

Формы прогиба стержня при различных значениях внешней приложенной распределенной нагрузки для первой моды решения можно представить следующим образом (рис. 4).

Таким образом, при последовательном применении аппарата эллиптических функций были получены точные аналитические решения задачи о геометрически нелинейном изгибе тонкого стержня под действием нормальной распределенной нагрузки. Эти решения имеют удобный для алгоритмических вычислений вид и позволяют подробно анализировать формы изгиба стержня.

Полученные выражения для форм изгиба стержня под действием нормальной распределенной нагрузки записаны в едином параметрическом виде в полярных координатах и зависят от величины нагрузки. Выражения представлены в эллиптических функциях Вейерштрасса и имеют более простой вид, чем решения, приведенные в работе [1]. Полученные результаты могут быть распространены на другие случаи других условий закрепления концов стержня.