Нелокальная краевая задача для нагруженного уравнения третьего порядка

Теория краевых задач для уравнений смешанного типа в силу ее прикладной и теоретической значимости в последние годы стало одним из важнейших разделов теории дифференциальных уравнений с частными производными.

Наряду с изучением классических типов уравнений внимание исследователей в последние годы все чаще уделяется изучению общих дифференциальных уравнений с частными производными, в частности смешанные уравнения третьего порядка.

Рассмотрим в области Q плоскости переменных ( x , y ) , уравнение:

Auxxx + Buxxy + Cuxyy + Du„y = F(x, У, U, Ux , uy , uyy , uxx )

с коэффициентами A,B,C,D зависящими от X и У. Если в каждой точке рассматриваемой области характеристическое уравнение:

A X + B X + C X + D = 0, где X = dy ,

dx

соответствующее уравнению (0) имеет одно действительное и два комплексных решений, а коэффициенты A, B, C, D в области Ω непрерывны вместе с производными первого порядка, то с помощью неособого действительного преобразования независимых переменных, уравнение (0) может быть приведено к виду

а

— A U = Fn Х , У , U , Ux , Uy , Uxx , Uyy , Uxy ).

Такие уравнения называются уравнениями составного типа и их исследованию посвящено большое количество работ, как российских, так и зарубежных авторов.

Рассмотрим дифференциальное уравнение в частных производных:

d

У ( u xx - u y ) - Л ^U ( x ^{,0 )}   У >  ⁰

0 = ^

dx uxx - uyy - X2u(x,0),  У < 0

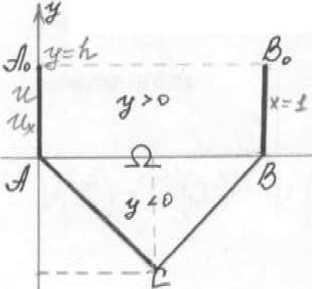
где: λ1 и λ2 – вещественные числовые параметры, в области Ω, ограниченной при У>0, отрезками АА0, А0В0 и В0В прямых Х=0, У=h и Х=I соответственно и характеристиками АС: Х+У=0 ВС: Х-У=I уравнения (1) при У<0

ЗАДАЧА: Найти регулярное в области Ω(У≠0)

решение u(X, У)уравнение (I), непрерывное в Q, обладающее непрерывными производными их и иу в области  Q \ BB0 о A0B0 u BC и удовлетворяющее условиям:

и Ix=0 = ^1(y),  и Ix=1 = ^2(yY ux 1 x=0 = ^3(y X  0 < y < h,

и Lс ⁼ V ( x ),  0 <  x < — .

При y > 0характеристическое уравнение имеет вид: (dy)3 = 0, y = const - кратные действительные характеристики, при y<0 характеристическое уравнение

( dy )² - ( dx )² = 0, y - x = C_Y ,   y + x = C₂

действительные

характеристики.

В силу непрерывности u ( x , y )| ₀= u ( x ) на основании уравнения (1) при У≥0, предварительно проинтегрировав полученной Х,

Т ( x ) -и ( x ) = K - Л J Т 5 ) ds ,                                                (4)

x где: К – неизвестная константа, подлежащая определению. Равенство (4) дает первое функциональное соотношение, принесенное на линию изменения типа из параболической части области Ω на линию y=0.

Второе функциональное соотношение между т ( x ) и и ( x ) , принесенное на y=0 из гиперболической части Ω 2 области Ω имеет вид:

f x ) Л x Г ^ + x )

и( x)-т ( x) = И-l-—Ы ——(5)

v2 j 2 о v 2

Исключив из (4) и (5), и ( x ) , из (5) имеем, что:

xx

• - l- 22          ld^-

• j        о х

Значение и ( x ) из (6) подставим в (4). В результате получаем, что:

[Л xx

-l+— Ы     W = K - ^Л | ^т ( ^ ) d ^ .

• 2    j   2 о v 2 jо

x

Если обозначить через: т"-т' = K - Л ,   ^ т ( ^) d ^ = f ( x )

о

x l-Л|т(^)d^

^{2 j}     о

-

о

т'' ( x ) - т' ( x ) = K - р( x ).

^ , получим

соотношение

Присоединяя к уравнению (7) начальные и граничные условия, получим одну из задач:

т"(x) -т'(x) = K - р( x)

краевых: т(о) = ^(о),  т(1) = ^ (о), или т’(о) = ^ (о),  т(1) = ^ (о), или начальную

г (о) = ^ 1 (о),   т' (о) = ^ з (о).

Второй интеграл в представлении р ( x ) преобразуем к виду:

- Л2 i Tf ^+xld^ = -Л2 j T(^)d^, тогда, P(x) = -W' fx о v       2x xx

- Л j t ( t ) dt - Л j t ( t ) dt .

о                x

После определения функции т ( x ) ), исходная задача в области Q₂ сводится к задаче А: найти регулярное в области Q₂ решение и уравнения (1) при y<0, непрерывное в О₂, обладающее непрерывными производными U_x и

U в области Ω BC и удовлетворяющее граничным условиям:

U I , = 0 = Т ( x )  ,   U\_AC = ^ф ( x ),

∂ U ∂ n

AC

= V 2 ⁽ x ),

где: n - внутренняя нормаль: t , v , V - заданные функции, причем T', V‘ , V‘ непрерывны, а в области Ω , приходим к решению задачи В: Найти регуляторное в области Ω решение уравнения (1), непрерывное в замкнутой области Ω и удовлетворяющее граничным условиям:

U| x = ₀ = ф 1 ⁽У ), U x _{= 1} = ф 2 ⁽ У ), U x|x = ₀ = ф з ⁽ У ), ⁰ ^ У ^ ^к

U\y=0 = Т(Х)  ’  0 - Х - 1, где: ф1,ф2,ф3,т - заданные гладкие функции, причем выполняются условия: Ф1(0) = т(0),ф2(0) = т(1),фз(0) = т'(0).