Неминимально-фазовая коррекция цифрового электропривода

Предлагается ввести в состав регулятора скоростного электропривода неустойчивое апериодическое звено. Показано, что использование неминимально-фазовой коррекции обеспечивает подавление колебаний, возникающих при увеличении периода квантования по времени цифрового регулятора скорости.

Как известно, неминимально-фазовыми называют звенья, у которых хотя бы один нуль или полюс их передаточных функций является правым [1]. При синтезе коррекции с помощью аппроксимированных амплитудных частотных характеристик (ЛАЧХ) неминимально-фазовые корректирующие звенья обычно не используют, хотя их техническая реализация трудностей не вызывает, особенно, если она выполняется программным путем [2]. Это связано с отсутствием у неминимально-фазовых звеньев однозначной связи между амплитудными и фазовыми частотными характеристиками и невозможностью тем самым оценивать переходные процессы по виду ЛАЧХ [3].

Рассмотрим свойства замкнутого по скорости электропривода постоянного тока с малоинерционным преобразователем в цепи якоря. На линеаризированной структурной схеме (рис. 1) преобразователь П представлен апериодическим звеном с постоянной времени Т_п=0,001 с. Это малая постоянная, которая учитывает в том числе «паразитные инерционности» элементов контура. Двигатель Д представлен в виде последовательного соединения двух апериодических звеньев с постоянными времени якорной цепи Т_я=0,004 с и электромеханической постоянной Т_м=0,01 с. При Т_МЯ34Т_Я такое представление вполне допустимо. Регулятор скорости (PC) выполнен как пропорциональнодифференциальное звено с фильтрацией, где постоянная времени инерционной части Тг^Т,. Все переменные на схеме (рис. 1) выражены в долях от базовых значений, соответствующих номинальному напряжению на якоре и_я = Ur _ном

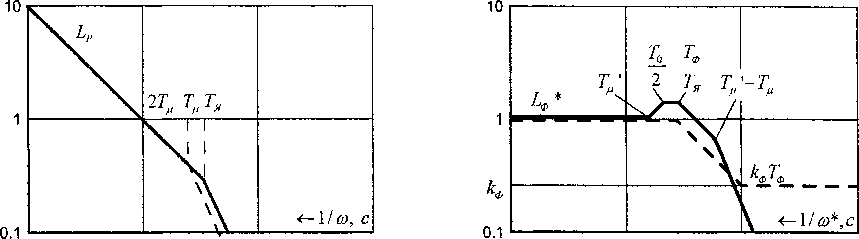
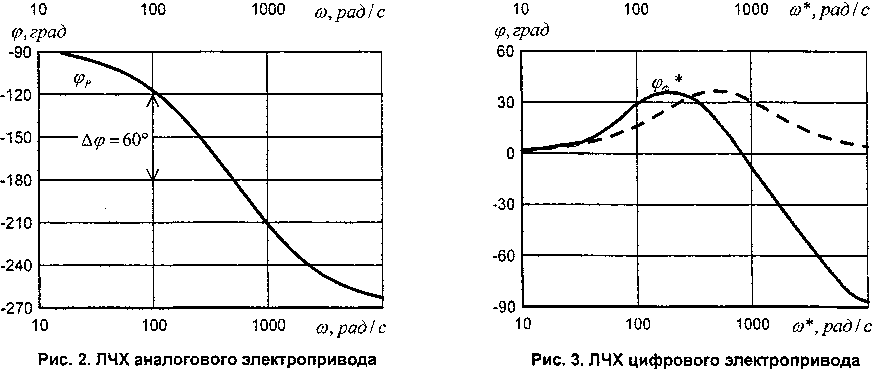
Стандартной настройке электропривода на «технический оптимум» соответствуют ЛАЧХ и ЛФЧХ, представленные на рис. 2. Контурный коэффициент передачи ХР= 100 задается, исходя из требуемой точности отработки задания (Аю = 1 % ).

Частота среза системы ®с=—— определяется 27^

суммой малых «некомпенсируемых» постоянных времени контура

Т„ =ТЯ+ТП =0,004 + 0,001 = 0,005 с.

Постоянная времени дифференцирующего канала регулятора выбирается равной наибольшей из по стоянных времени инерционных элементов объекта 7) = Гм = 0,01 с. Наконец, постоянная времени инерционного (фильтрующего) канала получается Т2 = КР- П^ =100-2-0,005 = 1 с. Переходный процесс на выходе системы при скачке задания, соответствующий выбранной настройке электропривода, протекает с небольшим перерегулированием (рис. 6,а) и заканчивается за время

^(З-А^+Т^

= (3.. .4) (0,01 + 0,005) = (0,045.. .0, Об) с.

При программной реализации регуляторов важное значение приобретает правильный выбор периода квантования (дискретизации) по времени Го. При малых значениях То (например, для нашего случая Го < 0,001 с) влиянием дискретизации можно пренебречь и рассматривать электропривод как обычную непрерывную систему. Однако при этом время, отводимое для вычисления управляющего воздействия, сокращается и, как следствие, от реализации сложных управляющих алгоритмов приходится отказываться и применять наиболее простые в ущерб точности, быстродействию и другим важным характеристикам привода. Если же необходимо реализовать сложный алгоритм управления, то приходится применять более быстродействующие, а значит и более дорогие микропроцессоры (чаще специализированные) которые, как правило, обладают избыточными функциями, за которые тоже надо платить [4].

При увеличении То (например, 0,001 < Г0<0,01) появляется возможность использовать дешевые микроконтроллеры общего назначения с меньшим быстродействием, так как времени на периоде квантования То теперь достаточно для обработки информации от датчиков и формирования воздействий при сложных алгоритмах управления. В то же время увеличение То >0,01 может привести к неустойчивости системы даже и в том случае, если непрерывная часть обладает достаточными запасами по устойчивости [5]. Предельным значением периода квантования То, увеличивать который без потери работоспособности системы недопустимо, является 2

^пред _ —, где ^ _ частота Среза непрерывной ®с системы [5]. Для рассматриваемого примера (рис. 1)

PC

п-д при

СО г\=----

2?;

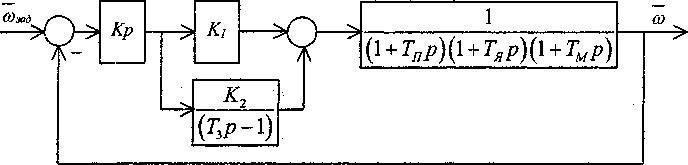
Рис. 1. Структурная схема электропривода

= 100 рад/с максимально допустимой

величиной ■ периода дискретизации является

Го = 74*” =0,02 с.

Наиболее наглядно влияние дискретизации можно выявить с помощью псевдочастотных ЛЧХ [6]. Для рассматриваемого примера (рис. 1) в области малых частот го < ®_с Ц ^®*) = Lp (го),

* 2   ( ГЛ , где ® = —tg ®— , рад/с - размерная псевдочас-т; У 2 у

2        ( Т Л тота. Так как при го<юс ю<—, то tg го— ®

То        к 2 у

«®— и го*« го. В области высоких частот 2

го > гос передаточная функция непрерывной части может быть записана так:

®с ®с

⁼ р(Т_яр ₊ 1)(Г_пр ₊ 1) ” р(т„р ₊ 1)

fi т; )

V ^Т.Р^)

1 nn (1 - 0,005w) (1 + 0,00155w) “ w(l + 0,00655w) "

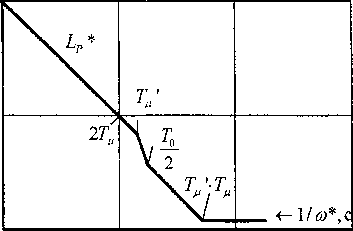
Последнее выражение позволяет определить частотные характеристики цифрового электропривода как функции псевдочастоты (рис. 3). Из рис. 3 видно, что учет дискретизации по времени приводит к значительному увеличению отстающей фазы при частоте среза ю*_с = <в_с = 100 рад/с. Если в непрерывной системе запас устойчивости по фазе составил ^ф = 60° (рис. 2), то в дискретной системе с То = 0,01 с он уменьшился до величины (хф* = 36°. Для того, чтобы приблизить динамические характеристики цифрового и аналогового электроприводов в контур регулирования может быть введен дополнительный дискретный фильтр с ЛАЧХ L^Lp-I^ и ЛФЧХ Ф_Ф«^Фр-^ (рис. 4). Так как to * го при го хв^, характеристики Ьф и C^, ф_ф и ф_ф близки лишь в среднечастотном диапазоне, когда го превышает го^ примерно в (2...4) раза. На высоких частотах (®*> 10®;) расхождения амплитудных Т_ф и Т^ и

Переходя к w-форме при использовании подста-2 е^рТ» -1

новки w =--^--- д ля прямоугольных импуль-

То ер 0 +1

сов получаем [6]:

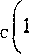
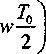
i+wt;

где

7 А

1 ^Tv

1-е '

Примем

m Гред 0,02

Т_о= —— =--- = 0,01 с, тогда

2      2

7/- 0,00655. Передаточная функция разомкнутого

контура

^(w) = toc

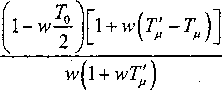
фазовых фф и ф*_ф характеристик более заметны. Однако при выборе структуры фильтра указанным различием характеристик можно пренебречь.

Особенность характеристик (рис. 4) состоит в том, что «падающему» виду желаемой ЛАЧХ фильтра должна соответствовать опережающая фаза при частотах, близких к частоте среза непрерывной части. Такой вид ЛЧХ имеет неминимально-фазовое звено с передаточной функцией

Если выбрать Т_ф = Т_я = 0,004 с, а Аф=0,25 < 1 и, следовательно, к_фТ_ф = 0,25 • 0,004 = 0,001 с = Т_п, то аппроксимирующие ЛАЧХ и ЛФЧХ (они показаны на рис. 4 штриховыми линиями) будут близки к желаемым. При необходимости максимум штриховой опережающей фазы может быть смещен влево путем соответствующего выбора параметров Тф и кф. ■

К сожалению, введение в контур дополнительного фильтра, формирующего на выходе сигнал,

100         1000 ш*,рай!с

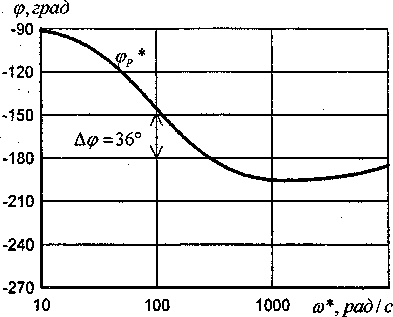
Рис. 4. Желаемые ЛЧХ цифрового фильтра

пропорциональный отрицательной производной входа, приводит к неустойчивости непрерывной и тем более импульсной систем. Сказанное побуждает к поиску нестандартных подходов к синтезу регуляторов высокоточных электроприводов [7, 8]. Один из возможных вариантов нетрадиционного построения регулятора показан на рис. 5. По сравнению с обычным исполнением (рис. 1) здесь вместо дифференциального канала использовано неустойчивое апериодическое звено с коэффициентом передачи к2 и постоянной времени Г3. В отличие от исходной схемы (рис. 1), где коэффициент передачи пропорционального канала кх принимался равным единице, здесь кх может варьироваться в широких пределах. Необходимость в дополнительной фильтрации отпадает, поэтому Т2 = 0. Передаточная функция регулятора, соответствующая схеме на рис. 5, имеет вид:

к Т где k_vc = к₂-к^; Г₄ = -~-. к₂ -к_х

Получается необычное реальное форсирующее звено, с помощью которого при к^ > к_х и, следовательно, Т₄<  Т₃ возможно реализовать эффективную запаздывающую коррекцию.

Если отнести к_РС в состав контурного коэффициента передачи системы, условия выбора параметров к_х, к₂, Т₃ при настройке на технический оптимум запишутся так:

к Т т3 = к^с ■ кр-т4; т4=-^- = тм. к2-к3

Отсюда, при К? =100 получаем ^ = 0,01; 7^3=А2—^1=^2— 0,01. В частном случае, при к₂= 1,001 коэффициент передачи регулятора £_РС⁼Е а фильтрующая постоянная времени Г₃ = 1 с. Амплитудная характеристика разомкнутого контура с новой коррекцией в точности совпадает с ис-

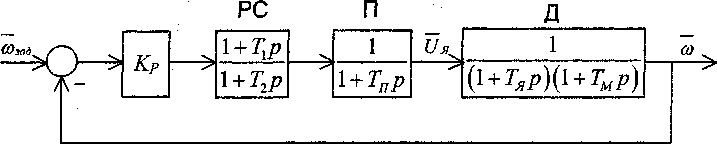
Рис. 5. Структурная схема электропривода с неминимально-фазовым регулятором

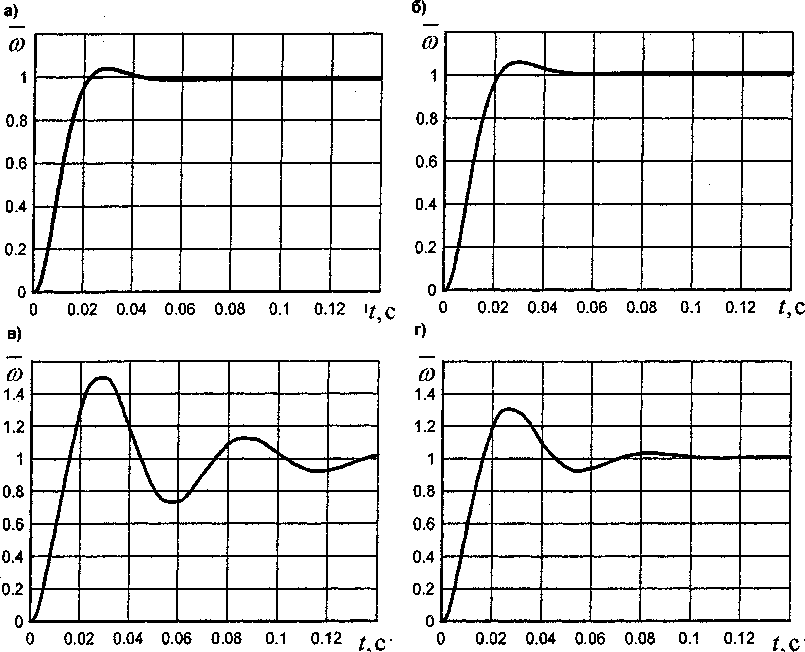
Рис. 6. Переходные процессы в аналоговом и цифровом приводе

хоДной ЛАЧХ (рис. 2). Фазовые же характеристики в области низких частот существенно различаются. Если в исходной системе (рис. 1) отстающая фаза с ростом частоты равномерно увеличивается от 0° до 270°, то в схеме (рис. 5) она изменяется от -180° до -270° с существенным подъемом в области средних частот, компенсирующим отстающую фазу наиболее инерционного звена объекта. Подъем фазы с уровня -180° до уровня -90°, осуществляемый неминимально-фазовым звеном, свидетельствует как бы о появлении в контуре фиктивного форсирующего звена с постоянной времени 7фиет = 7з- Это обстоятельство благоприятно отражается на динамике контура. В этом можно убедиться, если проанализировать переходную характеристику регулятора

^(0 ^{= -}(^2 + к^ + к₂е^Тз .

Для рассматриваемого численного примера при кх = 0,01; к₂ = 1,01; Г₃ = 1 с получаем

Л(г) = -1 + 1,01е'.

При t = 0 h(t) = кх = 0,01; при t -» оо h(f) -» оо. Форсировка, которую создает неминимальнофазовое звено, более эффективна даже в сравнении с обычным интегральным регулятором. Если в интегральном регуляторе h(t) - это линейно-нарастающая функция, то здесь - нарастающая, но не по линейному, а по экспоненциальному закону.

Расчет переходных процессов в системах (рис. 1, рис. 5) с помощью ЭВМ также доказывает эффективность рассматриваемой коррекции. На рис. 6 показаны диаграммы рассчитанных переходных процессов. При этом, на ЭВМ моделировались как режимы работы систем с непрерывным корректирующим звеном (рис. 6а - для классической коррекции, рис. 66 - для неминимальнофазовой коррекции), так и режим работы с дискретным корректирующим звеном с периодом квантования То = 0,01 с (рис. 6в - для классической, рис. 6г - для неминимально-фазовой коррекции). Сравнивая характер переходного процесса (рис. 6г) в системе с неминимально-фазовым регулятором и характер процесса в системе с классиче- ским регулятором (рис. 6в) можно убедиться в том, что при неминимально-фазовой коррекции максимальное перерегулирование составляет 27 %, то есть почти в два раза меньше, чем при обычной коррекции. Время затухания колебаний при использовании классического регулятора составляет 0,2 с (рис. 6в) против 0,1 с в случае неминимальнофазовой коррекции (рис. 6г).

Таким образом, усиление фильтрующих свойств системы, а также формирование на входе непрерывной части возрастающей функции веса w^t) = —— создает необходимые предпосылки dt для устранения колебаний, связанных с увеличением периода дискретизации.