Необходимые условия оптимальности квазиособых управлений в задаче оптимального управления стохастической системой с запаздывающим аргументом

Стохастические дифференциальные уравнения с запаздывающим аргументом являются адекватным математическим аппаратом при описании многочисленных явлений в теории автоматического регулирования, механике, биологии, экономике и радиофизике [1 –6] .

В статье рассматриваются системы управления, математические модели которых задаются нелинейными стохастическими дифференциальными уравнениями с запаздывающим аргументом и диффузными компонентами. Это позволяет учитывать действующие на систему случайные возмущения непрерывной природы.

Принцип максимума Понтрягина для различных задач оптимального управления стохастическими системами с запаздывающим аргументом получен в [7 –11] . В [9] рассмотрен особый случай вырождения условия максимума и получено необходимое условие оптимальности

(О К. Б. Мансимов, Р. О. Масталиев, 2020

(О Институт Систем Управления НАНА, 2020

Y-4.0

для особых в смысле принципа максимума Понтрягина управлений. Это рассмотрение также приводится в [12] .

Известно (см. [12] ), что особые, в смысле принципа максимума Понтрягина, управления являются также квазиособыми. Обратное неверно, т.е. квазиособые управления могут и не быть особыми, в этом смысле.

Необходимые условия оптимальности квазиособых управлений позволяют получить дополнительную информацию об управлениях, не являющихся особыми в смысле принципа максимума. Оптимальность в этом классе имеет сравнительно простую структуру, что важно с точки зрения проверки.

Предлагаемая работа посвящена выводу необходимых условий оптимальности квазиособых управлений в задачах оптимального управления, описываемых стохастическими системами с запаздывающим аргументом. В ней установлены необходимые условия оптимальности первого и второго порядков (линеаризованный принцип максимума и необходимое условие оптимальности квазиособых управлений).

Рассмотрение использует стохастический аналог метода, предложенный и развитый в работах К.Б.Мансимова (см., например, [13 –15] ) для детерминированных задач оптимального управления.

• 1.    Постановка задачи

Пусть (П, F, P ) — полное вероятностное пространство. Рассмотрим n-мерный стандартный винеровский процесс w(t), определенный на полном вероятностном пространстве (П,Е,Р ). Обозначим L F (t o ,t 1 ; R ⁿ ) пространство измеримых по (t, ш) случайных процессов

x(t,w) : [t0,t1] : П ^ Rn, для которых E Jt1 ||x(t)^2dt < +то, где E — знак математического ожидания.

Допустим, что поведение динамического объекта на отрезке времени t е T = [to,t1] описывается следующей системой стохастических дифференциальных уравнений с запаздыванием dx(t) = ft, x(t), x(t — h), u(t)) dt + ft, x(t), x(t — h)) dw(t),

• ⁽¹⁾    t ^{е (t} o ,t i ^], h >  0,

с начальными условиями

• (2)                 x(t) = Ф(t) при t G E t o = [t o - h, t o ),

• (3)                 x(t o ) = x o .

Здесь

x(t) G L F (t o , t 1 ; R n ) — вектор состояния;

f (t,x,y,u) — заданная n-мерная вектор-функция, непрерывная по совокупности переменных вместе с частными производными по (x,y,u) до второго порядка включительно, причем y(t) = x(t — h);

a(t,x,y) : T x R n x R n ^ R n^n — (n _x п)-мерная матричная функция, непрерывная по совокупности переменных вместе с частными производными по (x, у) до второго порядка включительно;

Ф(t) G L F (t o — h,to; R n ) — почти наверно (п.н) непрерывная на E _{t 0} начальная вектор - функция;

t ₀ и t ₁ — заданные моменты.

Определим множество допустимых управлений U d формулой

• (4)      u(t) G U d = {u() G LF, (t o ,t i ; R r )/u(t) G U C R r , п.н.} ,

где U — заданное непустое, ограниченное и выпуклое множество, и назовём процесс (u(t),x(t)) допустимым процессом.

В дальнейшем предполагается, что функция f (t, x, y,u) и матрица o(t,x,y) удовлетворяют условиям гладкости типа [16,17], обеспечивающим существование единственного решения системы (1) - (3) при каждом допустимом управлении u(t), t G T.

Наша цель — минимизировать на множестве допустимых управлений критерий качества

• (5)                          S(u) = E {ф(x(t 1 ))} ,

• 2.    Необходимое условие оптимальности первого и второго порядков

где ф(x) — заданная дважды непрерывно дифференцируемая скалярная функция.

Допустимое управление u(t), доставляющее минимум функционалу (5) при ограничениях (1) - (3) , назовем оптимальным управлением, а соответствующий процесс (u(t),x(t)) —оптимальным процессом.

Пусть (u(t),x(t )) — оптимальный процесс. Обозначим (u(t),x(t)) = (u(t) + Au(t), x(t) + Ax(t))

произвольный допустимый процесс и запишем формулу для приращения функционала

• (6)         AS(u) = S (u) — S(u) = E {ф(x(t ₁ )) — ф(x(t ₁ ))}.

Приращение траектории Ax(t) удовлетворяет системе dAx(t) = d[x(t) — x(t)] =

• (7)          = ff ( t,x(t),y(t),u(t) ) - f (t,x(t),y(t),u(t)))dt+

+ f^(t, x(t), y(t)) — a(t,x(t),y(t)))dw(t), t E (W i ],

• (8)    Ax(t) = 0, t E E t ₀ .

Пусть ^(t) E LF(to, ti; Rn) — случайный процесс, стохастический дифференциал которого имеет вид d^(t) = a(t)dt + в (t)dw(t), где a(t) — n —мерная измеримая и ограниченная функция. Тогда из формулы Ито [16–18] вытекает, что d(^‘(t)Ax(t)) = d^’ (t)Ax(t) + ^‘(t)dAx(t) + e(t)[CT(t,x(t),y(t)) —

• —    ^(t,x(t),y(t))]dt =

= d^ ‘ (t)Ax(t) + ^ ‘ (t)[ f f ( t,x(t),y(t),u(t) ) —

• —    f (t,x(t),y(t),u(t))^dt+

• (9)                       + ^(t ,x(t) , y(t)) — a ( t ,x(t), y(t))dw(t)]+

+ e(t) [^(t, x(t), y(t)) — a(t,x(t),y(t))]dt,

Здесь, и в дальнейшем, ( ^′ ) означает операцию транспонирования, а для векторов скалярное произведение.

Введем стохастический аналог функции Гамильтона-Понтрягина и ряд обозначений, позволяющих упрощать записи формул H (t,x,y,u,^) = ^'f (t,x,y,u),

Hx [t] = Hx(t,x(t),y(t),u(t),^(t)), Hy [t] = Hy (t,x(t),y(t),u(t),^(t)), Hu [t] = Hu(t,x(t),y(t),u(t),^(t)), Hxx [t] = Hxx(t,x(t),y(t),u(t),^(t)), Hxy [t] = Hxy (t,x(t),y(t),u(t),^(t)), Hyx [t] = Hyx(t,x(t),y(t),u(t),^(t)), Hux [t] = Hux(t, x(t) , y(t) , u(t) , ^(t)), Huy [t] = Huy (t,x(t),y(t),u(t),^(t)), Huu [t] = Huu(t,x(t),u(t),^(t)), fx [t] = fx t x(t) y(t) u(t) fu[t] = fu(t,x(t),y(t),u(t)), ^y [t] = ^y (t,x(t),y(t)),

f y [t] = f y t, x(t), y(t), u(t) CT x ^[t] = CT x (^t,x(t),y^(t)) , ^ xx [t] = CT xx (t,x(t),y(t))

Введенные обозначения позволяют представить формулу (9) в виде:

d(^ ' (t)Ax(t)) = d^ (t)Ax(t) +

+ [H (t,^x(t),u(t),WM(t)) - H(t,x(t),y(t),u(t),^(t))]dt+ +^ ' (t)^CT(t,x(t),y(t)) - ff(t,x(t),y(t)))dw(t)+

• (10)              +e(t)(^(t,x(t),y(t)) - a(t,x(t),y(t))^dt

С учетом (8) и (10) , выражение (6) принимает следующий вид:

AS(u) = E^(x(t 1 )) — ф(x(t ₁ )) + ^ ' (t 1 )Ax(t 1 ) — j^ d^ ' (t)Ax(t) -

• - It ^(t,x(t),y(t),u(t),^(t)) — H(t,x(t),y(t),u(t),^(t))^dt — j_t e(t)(^(t,x(t),y(t)) — a(t,x(t),y(t))^dt j.

  
  

Используя формулу Тейлора, получим:

AS(u) = E^ X (x(t x ))Ax(t i ) + |Ax ' (t i>xx (x(t i ))Ax(t i ) + ^ ' (t i )Ax(t i ) -

- / ¹ d/(t)Ax(t) - / ¹ H [t]Ax(t)dt - [ ¹ H [t]Ay(t)dt - [ ¹ H U [t]Au(t)dt - 00    0 t 0

2 у t ¹ Ax ‘ (t)H xx [t]Ax(t)dt+ у t ¹ Ax ‘ (t)H xy [t]Ay(t)dt + ^ t ¹ Ay ‘ (t)H yx [t]Ax(t)dt+

+ / Ay‘(t)Hyy [t]Ay(t)dt + / Au' (t)Huu[t]Au(t)dt+ t0

+ 2 / Au'(t)HUX[t]Ax(t)dt+2 / Au'(t)Huy[t]Ay(t)dt -t0

Уt1 e(t)^X [t]Ax(t)dt - уt1 WW^ [t]Ay(t)dt-1 t1                                                  1

2 J Ax ' (t)e(t)^ xx [t]Ax(t)dt - ^ у Ay ' (t)e(t)ff yy [t]Ay(t)dt -

2 у Ax ' (t)e(t)ff xy [t]Ay(t)dt - 2 у Ay ' (t)e(t)ff yx [t]Ax(t)dt| + n(Au),

8                    К. Б. Мансимов, Р. О. Масталиев

где по определению

n(Au) = E^o i ( | Ax(t i ) | 2 ) - У t1 o ₂ ([ | Ax(t) | + | Ay(t) | + | Au(t) | ] ² )dt - у t 1 в (tb([||Ax(t) || + | Ay(t) | ] 2 )dt|.

Здесь, по определению, величины oi(^), О2(^), и оз(^) определяются соответственно из разложений фИ^)) — фИ^)) =

= ф X (x(t 1 ))Дx(t 1 ) + 2 Ax ' (t i )ф хх (x(t i )) Ax(t i ) + o i ( ^ Ax(t i ) ^ ² ),

H (t,^x(t),y(t),u(t),^(t)) - H(t,x(t),y(t),u(t),^(t) ) =

= H X [t]Ax(t) + H [t]Ay(t)+H U [t]Au(t)+

+ jAx ' (t)H xx [t]Ax(t) + |Ax ' (t)H xy [t]Ay(t)+

+ ^Ay ' (t)H yx [t]Ax(t) + Au ' (t)H ux [t]Ax(t)+

+ Au ' (t) H uy [t]Ay(t) + jAu ' (t)H uu [t]Au(t)+

+ 0 2 ([ ^ Ax(t) ^ + || Ay(t) || + || Au(t) ||² ), a(t,x(t) , y(t)) - a ( t , x(t), y(t)) =

= a X [t]Ax(t) + a y [t]Ay(t) + 2Ax ' (t)o xx [t]Ax(t)+ ^y             2

+ jAx ' (t)ff xy [t]Ay(t) + jAy ' (t)ff yx [t]Ax(t)+

+ o 3 ([ ^ Ax(t) ^ + || Ay(t) || ] ² ).

Предположим, что случайные процессы ^(t) е L F (t ₀ ,t _i ; R n ) и e(t) е L F (t o ,t _i ; R ^nxn ) являются решением следующей системы стохастических дифференциальных уравнений:

' d^(t) = — [H _x [t] + H _y [t + h] + в (t + h)a _y [t + h]] dt+ + e(t)a _x [t] + в (t + h)dw(t),

t е (to, ti — h], d^(t) = — [Hx [t] + e(t)ax[t]]dt + e(t)dw(t), t е [ti — h,ti],      —^(ti) = фx(x(t1)).

Уравнение (13) назовем стохастической сопряженной системой в рассматриваемой задаче.

Отсюда принимая во внимание (13) , приращение функционала качества (11) , с помощью очевидных преобразований представляется в виде:

AS (u) = E

[^— L

H U [t]Au(t)dt + 2 |Ax ' (t i>xx (x(t i ))Ax(t i ) —

1.1

t 0

Ax ' (t) [H xx [t] + e(t)^ xx [t ]] Ax(t)dt -

1.1

t 0

Ax ' (t) [H xy [t] + в(^)О ху [t ]] Ay(t)dt —

1.1

t 0

Ay ' (t) [H yx [t] + в (t) O yx [t] ] Ax (t) dt —

1.1

t 0

^A y ' ^(t) [H yy ^{[t] + e(t)} ° yy ^[t]] ^Ay^{(t) dt} -

t 0

Au (t)H ux [t]Ax(t)dt - 2

I ’1

t 0

Au (t)H uy [t]Ay(t)dt -

I ’1

t 0

Au (t)H uu [t]Au(t)dt

+ n(Au).

Пусть v(t) E L F (t ₀ ,t 1 ; R r ) — произвольная измеримая вектор-функция, а е E [0,1] — произвольное число.

Поскольку по предположению множество U выпуклое, то специальное приращение Au _e (t) допустимого управления области управления u(t) можно определить по формуле (см. напр. [12 , 13] )

• (15)                   Au _e (t) = е [v (t) — u(t)], t E T,

где v (t) E L F (t o , t 1 ; R r) — произвольная измеримая вектор-функция, а е E [0,1] — произвольное число.

Обозначим через Ax _e (t) специальное приращение траектории x (t), отвечающее приращению (15) допустимого управления u (t).

Из (7) , используя условие Липшица, при помощи леммы Гронуолла-

Белмана (см., например, [19] ) получается оценка

E (||Axe (t) ||) < Ne, где N = const > 0 и n (Aue (t)) = ° (e2).

Используя оценку (16) и формулу (15) из (7) по схеме, аналогичной [12, 13] , получаем справедливость утверждения

Лемма. Для специального приращения Ax _e (t) траектории x(t) системы (1) - (3) имеет место следующее разложение

Axe (t) = el (t) + o (e; t), где l(t) является решением задачи di(t) = [fx [t]i(t) + fy [t]i(t - h)+fU[t](v(t) - u(t))] dt+ (18)              + (^[t]l(t) + ay, [t]l(t - h))dw(t), t g (to,ti], l(t) = 0, t e Et0.

Принимая во внимание (17) и оценку (16) , из (14) получаем, что

AS _e (u) = S(u(t) + Au _e (t)) — S(u(t)) =

= E{ - ^e / H u ^[t](v^(t)

- u(t))dt + 2l ' (t 1 )ф xx (x(t 1 ))l(t 1 ) -

j:

/:

/:

/:

l(t) [H xx [t]+ e(t)^ xx [t]] l(t)dt -

l ' (t) [H xy [t] + e(t)^ xy [t]] l(t - h)dt -

l ' (t - h) [H yx [t] + e(t)ff yx [t]] l(t)dt -

l ' (t - h) [H _yy [t] + e(t)ff _yy [t]]l(t - h)dt -

t 1

2/   (v(t) - u(t))'Hux[t]l(t)dt- t0

2^ 1 (v(t)

— u(t) Y H uy [t]l(t — h)dt —

. ^t t 0

(v(t) — u(t)) 'H uu [t](v(t) — u(t))dt + o(e ² ).

Из разложения (19) и произвольности е е [0,1] сразу следует справедливость утверждения

Теорема 1. При сделанных предположениях для оптимальности допустимого управления u(t),t е T в задаче (1) - (5) необходимо, чтобы неравенство

E /“ t 0

H [t] (v(t)

— u(t))dt <  0

выполнялось для всех v(t) е L F (t o ,t 1 ; R r ).

Неравенство (20) является линеаризованным интегральным условием максимума для задачи (1) – (5) .

Используя лемму из [20 , c.8], можно показать, что это неравенство имеет место тогда и только тогда, когда почти для всех 9 е [t o , t 1 ) и v е L F (t ₀ ,t 1 ; R r ) выполняется

• (21)                       EH U [9](v — u(9)) <  0.

Из произвольности 9 е [t o , t i ) получаем, что

• (22)                   H U [9](v — u(9)) <  0 п.н.

• 3. Cлучай вырождения поточечного линеаризованного условия

где 9 е [t ₀ ,t 1 ) — . точка Лебега управления (правильная точка)u(t), (см. например, [21 , с.86-87]).

Неравенство (22) есть поточечный линеаризованный принцип максимума в задаче (1) – (5) .

максимума

• Следуя [12] , введем понятие квазиособого управления.

Определение 1. Если для всех 9 Е [t ₀ ,t 1 ) и v Е R^r

• (23)                   H U [9] (v — u(9)) =0 , п.н.

то допустимое управление u(t) называется квазиособым управлением.

Очевидно, что квазиособый случай поточечного линеаризованного условия оптимальности (22) (и, следовательно, условие (20) ) теряет свое содержательное значение, в связи, с чем надо иметь новые необходимые условия оптимальности.

Пусть u(t),t Е T квазиособое оптимальное управление. Тогда из разложения (19) в силу (22) и произвольности е Е [0,1] следует, что

E V(t 1 )ф xx (x(t i )) l(t i ) —

/ 4

t 0

l ' (t)[H xx [t]+ e(t)^ xx [t]]l(t)dt -

l ' (t) [H xy [t] + e(t)^ xy [t]] l(t - h)dt —

I" t 0

l ' (t — h) [H yx [t] + e(t)ff yx [t]]l(t)dt —

t t0

l' (t — h) [H yy [t] + e(t)^ yy [t]]l(t — h)dt —

2 / 1 (v(t) t 0

— u(t)) 'H ux [t]l(t)dt —

2 / 1 (v(t) t 0

— u(t)) 'H _uy [t]l(t — h)dt —

t 1

^— / ^{( v(t)}

t 0

— u(t)) 'H uu [t](v(t)

— u(t))dt

> 0.

Сформулируем полученный результат.

Теорема 2. Для оптимальности квазиособого управления u(t) в задаче (1) – (5) необходимо, чтобы неравенство (24) выполнялось для всех v(t) Е U, t Е T.

Как видно неравенство (24) есть неявное необходимое условие оптимальности квазиособых управлений, поэтому конструктивное использование этого условия оптимальности затруднительно. Однако, с его помощью удается получить ряд необходимых условий оптимальности квазиособых управлений, выраженных непосредственно через параметры задачи (1) - (5) . Займемся этим вопросом.

Уравнение (18) является линейным неоднородным стохастическим дифференциальным уравнением. Применяя результаты работы [9] , получаем, что решение l(t) задачи (18) допускает представление

^l(t)= [ ^R(t,TНФ) t 0

— и(т )) dr,

где по определению

R(t,T ) = Q(t,T )f u [T ].

Здесь фундаментальная матрица Q(t, t ) является решением однородного уравнения:

dQ(t,T ) = (f ‘x [t]Q(t,T ) + f [t]Q(t — h,T) ) dt+

• + (^CT X [t]Q(t, T ) + ст' у [t]Q ( t - h, T) ) dw(t),

Q(t,t) = I,

• (26)         Q(t,T) = 0, t > t,

где I — единичная матрица. С помощью представления (25) доказываются следующие тождества, которые будут использоваться в дальнейшем:

t 1

t 0

/ t1

t 0

Jt1

t 0

l ‘ ( t 1 ) ф xx ( x ( t 1 ) ) l ( t 1 ) = / / ( v ( t ) - u ( t ) ) ‘ R ( t 1 ,T ) ф xx ( x ( t ₁ ) ) R ( t ₁ ,s ) ( v ( s ) - u ( s ) ) dTds, t 0 t 0

l'( t ) [ H xx [ t ]+ e ( t ) ^ xx [ t ] ] l ( t ) dt =

= Г Г (v ( T ) - u ( T ) ) / ¹      R ( t, T ) [ H xx [ t ] + 0 ( 1)^ [ t ] ] R ( t, s ) dt ( v ( s ) - u ( s ) ) dsdT,

J t o     t o                          max( r,s )

l ‘ ( t ) [ H xy [ t ] + e ( t ) ^ xy [ t ] ] l ( t - h ) dt =

11           ′ t 1

=      /   (v ( t ) - u ( t )               R ( t,T ) [H xy [ t ] + e ( t ) ^ xy [ t ]] R ( t - h,s)dt v ( s ) - u ( s)) dsdT,

Jt o J t o                        max( r,s )

l ‘ ( t - h ) [ H yx [ t ] + в ( t ) ff yx [ t ] ] l ( t ) dt =

= / f  ( v ( T ) ^- u ⁽ T ) )'  /

J to J to                     J m

t 1

t 1

t 1

t 0

t 0

max( r,s )

R ( t - h, T ) [ H yx [ t ] + e ( t ) ^ yx [ t ] ] R ( t, s ) dt ( v ( s )

- u ( s)) dsdT,

t 0

l ( t ^- h ) [ H yy ^[t] + ^{в (t)} O yy ^[t] ] l ( t ^{- h)} =

= /   / (v(T) - u(T))Z  / o   to                        m

t 0

t 0

max( r,s )

R ( t - h, t ) [ H _yy [ t ] + в ( t ) ^CT _yy [ t ] ] R ( t - h, s ) dt ( v ( s )

- u ( s ) dTds,

/ ¹ ( v ( t ) - u ( t ) ) 'H ux [ t ] l ( t ) dt = / ¹

0                                             t 0

t 1

/   (v(t) - u(t)) Huy [t]l(t - h)dt = t0

( v ( t ) - u ( t ) )'H ux [ T ] R ( T,t ) dT^ ( v ( t ) - u ( t ) ) dt,

[It ^(t ) - u ( t ) ) ^иУ [ t ] R ( t - h, t)dT^ ( v ( t ) - u ( t ) ) dt.

Условия оптимальности квазиособых управлений             15

Полагая

K ( t, s) = - R(t i ,T )ф хх (x(t i )) R(t i ,s)+

+/ t 1 max( τ,s )

R(t,T ) [H xx [t] + e(t)^ xx [t]]R(t, s) +

+ R(t,T ) [H xy [t] + e(t)^ xy [t]]R(t - h,s)+

+ R(t - h, t ) [H yx [t] + e(t)^ yx [t]] R(t, s)+

+ R(t — h, t) [Hyy [t] + e(t)^yy [t]]R.(t — h, s) dt и учитывая тождества (27)-(33), неравенство (24) можно записать в следующем компактном виде:

E

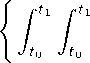
+ t1

V v ( t ) — u ( t )) K ( t, s) (v(s) — u(s)) dTds+

— u(t)) 'H uu [t] (v(t) — u(t))dt+

/   (v(t)

t 0

+ 2

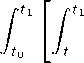
v^{v ( T} )

— u ( t ))' (H ux [ t ] R ( t, t)+

+ H uy [ t ] R ( t — h,t)) dT

I

(v (t) — u(t))dt j¹

< 0.

Заметим, что детерминированный аналог матричной функции K ( t, s) впервые введено в работах К.Б. Мансимова [13-15].

Сформулируем полученный результат.

Теорема 3. Для оптимальности квазиособого управления u(t), t ∈ T в задаче (1) – (5) необходимо, чтобы неравенство (34) выполнялось для всех v(t) е L F (t ₀ , t 1 ; R r ).

Как видно условие (34) является общим интегральным необходимым условием оптимальности квазиособого управления. Но используя различные специальные вариации управления, из этого условия можно получить целый ряд более легко проверяемых необходимых условий оптимальности. Приведем одно из них.

Теорема 4. Для оптимальности квазиособого управления u(t) в задаче (1) – (5) необходимо, чтобы неравенство

• (35)           E ( v — и(9) У H _uu [9] ( v — u(9)) <  0, п.н.

выполнялось для всех v е R r , 9 е [t o , t i ) - точка Лебега управления u(t) .

Для доказательства неравенства (35), достаточно в (34) v(t) определить по формуле fu(t), t е [to, 9),

• (36)                   v(t)= V, t е [9,9 + _M),

[u(t), t е [9 + ^, ti], где v е U, 9 е [to, ti), а ^ > 0 — произвольное достаточно малое число.

Тогда из формулы (34) получим

^E{(v — и(9) У H uu [9](v — u(9))| + o(^) <  0.

Отсюда в силу произвольности ^ > 0 и 9 е [t o , t i ) следует справедливость неравенства (35) .

Также не исключена возможность вырождения необходимого условия оптимальности (35) , т.е. его выполнения тривиальным образом.

Определение 2. Квазиособое управление u(t) назовем второго порядка квазиособым управлением, если для всех v е U, 9 е [t o , t 1 )

( v — и(9) У H _uu [9](v — и(9) У = 0, п.н.

Общее необходимое условие оптимальности квазиособых управлений (33) позволяет получить необходимые условия оптимальности для второго порядка квазиособых управлений.

Допустим, что u(t) второго порядка квазиособое оптимальное управление. Тогда принимая во внимание формулу (36) в неравенстве (34) , получаем неравенство:

E {(v — и(9) У [К(9, 9) + H ux [9\R(9, 9)] ( v — u(9))} <  0.

Здесь из произвольности 9 е [t o , t i ) получаем, что неравенство

• (37)       (v — u(9)) '[ K(9,9)+ H ux [9]R(9,9)](v — u(9)) <  0,

выполняется почти для всех 9 е [t o ,t 1 ) точек Лебега управления u(t), и v ∈ U.

Таким образом, доказано следующее утверждение.

Теорема 5. Для оптимальности квазиособого второго порядка управления u(t) в задаче (1) - (5) необходимо, чтобы неравенство (37) выполнялось для всех v е U и 9 е [t o , t 1 ).

Заметим, что необходимое условие оптимальности (37) является аналогом условия оптимальности Габасова-Кирилловой из [22] , полученный методом матричных импульсов для случая системы обыкновенных дифференциальных уравнений.

Авторы выражают глубокую благодарность рецензенту за ценные замечания по содержанию статьи.