Неоднородные киральные метаматериалы: анализ отражения оптических волн с учетом дисперсии материальных параметров

Современный этап развития компонентной базы устройств оптики и нанофотоники требует создания новых искусственных структур, обладающих уникальными свойствами взаимодействия с оптическими волнами. Одним из примеров таких структур являются метаматериалы [1 –4], которые представляют собой искусственные композиционные образования, состоящие из элементарных ячеек с субволновыми линейными размерами. Любой оптический метаматериал (ОММ) состоит из пространственной композиции атомов двух или более веществ. Как известно, свойства оптических метаматериалов определяются, прежде всего, именно пространственной конфигурацией и геометрической формой структур, которые входят в композиционную структуру [5–6]. В оптических метаматериалах их структурирование выполняется на микро- или наноуровнях. В этой связи можно говорить о том, что все оптические метамате- риалы являются пространственно неоднородными, а период их неоднородности соизмерим с длиной волны падающего излучения. Именно этот факт и приводит к тому, что результатом взаимодействия является возникновение новых свойств, которые не присущи материалам естественного происхождения.

Одним из типов ОММ является оптический ки-ральный метаматериал [7– 10], в структуру которого входят зеркально асимметрические атомные структуры. Киральность представляет собой свойство объекта не совпадать со своим отражением в плоском зеркале. Киральные ОММ позволяют, например, вращать плоскость поляризации оптической волны, а также все они обладают ярко выраженными частотно и поляризационно-селективными свойствами. Для описания киральных метаматериалов, помимо диэлектрической и магнитной проницаемости, вводится относительный параметр киральности, который определяется структурой и типом зеркально асимметричных образований в структуре композиции.

Общими свойствами киральных метаматериалов являются кросс-поляризация оптических волн (возникновение поляризованных компонент, отсутствующих изначально в падающем поле), а также совместное распространение волн с право- и левокруговыми поляризациями с различными фазовыми скоростями.

Одним из самых известных типов ОММ являются метаматериалы с отрицательным преломлением [11 – 15]. Идеи создания таких метаматериалов изложены в [16– 17]. Согласно их теории, показатель преломления метаматериала может быть отрицательным, что приводит к возможности нахождения преломленного луча по ту же самую сторону от перпендикуляра к границе раздела «диэлектрик–среда с отрицательным преломлением», что и падающего луча. Для создания таких искусственных структур необходима пространственная конфигурация, позволяющая в узком диапазоне длин волн достигнуть одновременных отрицательных значений диэлектрической и магнитной про-ницаемостей. Впервые такой метаматериал был синтезирован в СВЧ-диапазоне частот [18].

В работе [19] показано, что подобные среды могут быть использованы для создания так называемых суперлинз, при использовании которых можно преодолевать дифракционный предел.

Киральные метаматериалы описываются материальными уравнениями, в которых индукции электрического и магнитного полей связаны одновременно с напряженностями как электрического, так и магнитного поля. Эти дополнительные связи, отсутствующие в материальных уравнениях для однородных изотропных материалов, определяются именно параметром киральности. Различные формы записи материальных уравнений для киральных метаматериалов приведены в [7, 8, 20–22].

В настоящее время для частотной зависимости диэлектрической и магнитной проницаемостей метаматериалов используется общепринятая модель Друде– Лоренца [23–25], в которой для электрического и магнитного резонансов вводятся соответствующие, отличающиеся друг от друга, резонансные частоты. Для описания дисперсии параметра киральности используется модель Кондона [23, 26–27], которая изначально использовалась для описания оптической активности некоторых материалов естественного происхождения. В настоящее время исследованы также оптические волноводы, заполненные кираль-ным метаматериалом [28].

Заметим, что в большинстве используемых в настоящее время математических моделях киральных метаматериалов материальные параметры зависят только от частоты, то есть они являются однородными структурами, в которых дисперсия определяется именно пространственной конфигурацией атомов. При этом предполагается, что концентрация элементарных ячеек метаматериала неизменна по всей его толщине.

Интерес представляют неоднородные метаматериалы, у которых материальные параметры изменяются вдоль пространственных координат по какому-либо заранее заданному закону. Использование неоднородных киральных ОММ может привести к изменению характеристик оптической волны после ее взаимодействия с метаматериалом, по сравнению с однородными структурами. Здесь уместно заметить, что термины «однородный» и «неоднородный» относятся к макроуровню, в то время как на наноуровне все ки-ральные ОММ являются принципиально неоднородными или периодически неоднородными.

В данной работе рассматривается решение задачи о падении плоской линейно поляризованной оптической волны на планарный слой из кирального метаматериала, у которого все три материальных параметра являются неоднородными вдоль одной из координат.

Математическая модель однородного оптического кирального метаматериала

В основе математической модели лежат известные материальные уравнения для киральной среды [7, 8]:

D = S o S E + ix^ o ^ o H ; B = Ц о Ц H ± ix^ o V o E , (1)

где D – вектор электрической индукции; B – вектор магнитной индукции; E – вектор напряженности электрического поля; H – вектор напряженности магнитного поля; ε – относительная эффективная диэлектрическая проницаемость; µ – относительная магнитная проницаемость; χ – относительный параметр киральности метаматериала; ε 0 – электрическая постоянная вакуума; µ 0 – магнитная постоянная вакуума; i= - 1 – мнимая единица. Верхние и нижние знаки соответствуют киральной среде на основе правых и левых форм легированных химических соединений соответственно.

Материальные уравнения (1) являются частотно зависимыми вследствие пространственной дисперсии, возникающей в киральном метаматериале по причине соразмерности искусственных элементарных ячеек с длиной оптической волны. Дисперсионные зависимости диэлектрической и магнитной проница-емостей описываются моделью Друде–Лоренца, а параметра киральности – моделью Кондона [23–26]:

ε ( ω )

= ε c +

Ω ε ω 0 ²     ;

ω 02 -ω 2 + i γω

µ ( ω )

Ωµω2

= µ c +                ;

ω20 -ω2+iγω

χ ( ω ) =

Ω χ ω 0 ω ω 20 -ω 2 + i γω

где ω0 – резонансная частота; γ – частота демпфирования; Ωε, Ωµ, Ωχ – коэффициенты, определяющие отклонения значений материальных параметров метаматериала вблизи резонансной частоты ω0; εcµc – относительные диэлектрическая и магнитная проницаемости среды-контейнера, в которую легируются киральные атомы.

Данная дисперсионная модель описывает следующую физическую модель оптического кирального метаматериала: в структуру магнитодиэлектрика внедрены атомы зеркально асимметричных химических соединений (например, соединений, образующих оптически активные среды) или проводящие наноэлементы зеркально асимметричной формы. В данном случае дисперсия диэлектрической и магнитной проницаемостей метаматериала описывается дисперсионной моделью Друде–Лоренца, а вследствие зеркальной асимметрии нановключений дисперсия параметра киральности определяется формулой Кондона, которая использовалась ранее для описания оптически активных сред.

Соотношения (1) и (2) определяют математическую модель однородного кирального метаматериала:

—

D = S o S c +

^ S ^ 0 w 0 - w ² + i yw

—

E +

+ i у ^ о Ц о

^^w w 0 - w ² + i yw

—*

—

B = Ц о Ц с +

Q_Цw ² w 0 - w ² + i yw

—

H ±

± i ^0 Ц 0

Q_zro o ® w 0 - w ² + i yw

—

E .

Математическая модель неоднородного оптического кирального метаматериала

В данном случае материальные параметры ки-рального метаматериала будут зависеть от радиус-вектора точки, то есть будут являться функцией частоты и пространственных координат:

s = s ( r ; w ) ; ц = ц ( r ; w ) ; % = z ( r ; w ) .               (4)

С учетом соотношения (4) материальные параметры неоднородного кирального метаматериала будут иметь вид:

/ — x            ^sw 0 ( r )

^S ( r ;^w ) = ^S c ⁺ ——--——; w 0 ( r ) -w² + i yw

/ — x            ^^w 2 ( r )

ц ( ^r ; ^w ) = Цс ⁺ ——--——; w 0 ( r ) -w ² + i yw

/ — x      ^Q/w 0 ( r ) w

Z (r;w) =                    , w0 (r )-w + iyw

то есть резонансная частота будет принимать различные значения в разных точках, определяемых радиус-вектором r .

В дальнейшем в работе будем предполагать, что материальные параметры метаматериала будут изме- нять вдоль одной координаты x, которая определяет поперечное направление в структуре. В этом случае с учетом (4) и (5) математическая модель неоднородного кирального метаматериала принимает следующий вид:

——

D = S 0

^w 2 ( x )

w 2 ( x ) -w ² + i yw

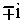
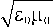
Q_zw ₀ ( x ) w w 0 - w ² + i yw

——

——

B = Ц 0

Q_Цw ² ( x ) w 2 ( x ) -w ² + i yw

—

H ±

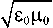
Q_zw ₀ ( x ) w w 2 ( x ) -w ² + i yw

Постановка задачи

Рассмотрим падение оптической волны линейной ( s или p ) поляризации на слой оптического кирально-го метаматериала, описываемого математической моделью (6). Геометрия задачи приведена на рис. 1. Будем считать, что области 1 и 2 на рис. 1 – вакуум; область 2 — неоднородный планарный слой кирального метаматериала, который описывается материальными параметрами s , ц и z - Угол падения волны обозначим через 0 ; толщину планарного слоя - через L . Амплитуда напряженности электрического поля падающей волны – E 0 .

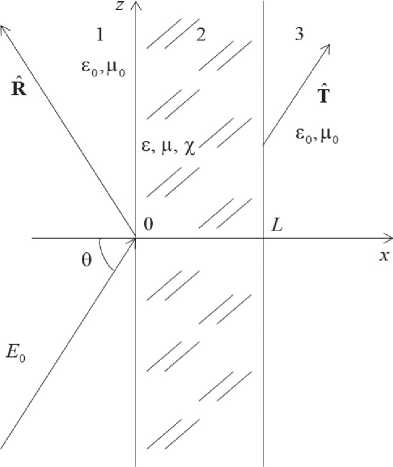
Рис 1. Геометрия задачи

При решении будем учитывать явление кроссполяризации поля, то есть при падении s - поляризованной волны в структуре отраженного и прошедшего полей будут присутствовать составляющие, соответствующие p - поляризованной волне и обратно.

В этом случае можно ввести матрицы коэффициентов отражения R и прохождения T следующего вида:

л

R =

г R ss l R PS

R ^sp ]

R pp J

т ss

T ps

T sp

T I , pp J

где через R и T обозначены коэффициенты отражения и прохождения соответственно; l , m = {s, p} при l = m значения коэффициентов соответствуют основной (падающей) компоненте оптического поля; при l ^ m -кросс-поляризованной компоненте оптического поля.

Следует заметить, что в общем случае отраженная и прошедшая волны будут иметь эллиптическую поляризацию.

Методика решения

Для общности решения введём в рассмотрение следующие нормированные (безразмерные) физические и геометрические параметры: нормированную координату С = x / L ; нормированные волновые числа: K = « L / c ; K y = Y L / c ; K 0 ( ^ )= « 0 ( c ) L / c ; нормированные пространственные зависимости y - и z -составляющих напряженностей электрического и магнитного полей в неоднородном слое метаматериала: U 1 ( C ) = E v ( С )/ E о ; и 2 ( С ) = E z ( С )/ E о ; V 1 ( С ) = Z о H z ( C )/ E о ; V 2 ( C ) = z H ( C )/ e 0 . Здесь введены следующие обозначения: Z 0 = -^ ц ₀ / £ ₀ -характеристическое сопротивление вакуума, c – скорость света.

Также перейдем к нормированным переменным в выражениях для материальных параметров метаматериала (6):

K ; = £ ^{П к} ;

^{( Л)} c K 00 ( С ) - K ² + i K _Y K’

ц ( k ; С ) = р +

П р k ²       .

K о ² ( С ) - к ² + i K Y к ’

х ( K ; С ) =

Пк о(С)к к о2 (С)- к2 + i кY к ■

В случае гармонической зависимости векторов электромагнитного поля от времени вида exp(i « / ) система уравнений Максвелла относительно нормированных напряженностей электрического и магнитного полей в слое неоднородного метаматериала имеет вид:

d d С	U 1 ( С ) ' V 2 ( С ) _	= A 1 ( С ; к )	U 2 (С)' . V ( c ) .
d d С	■ U 2 ( С ) ‘ _ V ( C ) .	= a 2 ( С ; к )	( [ V ( С ) ]

0 13 ( С ; к ) a 12 ( С ; к ) a 43 ( с ; к ) a 42 ( с ; K )

a 31 ( С ; к )   a 34 ( С ; K )

a 21 ( c ; к )   a 24 ( c ; K )

Коэффициенты матриц A 1 ( С , K ) и A ₂( С , K ) имеют следующий вид:

a i2 ( С ; K ) = - i K ц ( С ; K ) ; a 43 ( С ; K ) = i K s ( C ; K ) ;

a 24 (С; K) = - K х(С; K )х

L              sin2 0'

х 51 +--;------;—;------;-------;г г;

[ ц ( С ; к )_е( С ; к ) -х ² ( С ; к )

a 13 ( С ; к ) = a 42 ( С ; к ) = к х ( С ; к ) ;

a 31 (С; к) = a 24 (С; K);(11)

a 34 (С; к) = i к ц(С; K )х х |1sin2 0|,

^х[ ц ( С ; к )_е( С ; к ) -х ² ( С ; к ) ^;

a 21 ( С ; K ) = i K s ( C ; K ) х

Lsin2 0'

х[   ц(С; к )е(С; к )-х2 (С; к ).

Запишем граничные условия при x =0 для случая падения волны перпендикулярной ( s ) поляризации:

U 1 ( о ) = 1 + R ss ; V ( о ) = ( 1 - R ss ) cos 0 ;

U 1 ( 1 ) = T ss ; V 1 ( 1 ) = T ss cos 0 ;

U 2 ( 0 ) = - R sp cos 0 ; V 2 ( 0 ) = - R sp ;

U 2 ( 1 ) = T sp cos 0 ; V 2 ( 1 ) = - T sp .

По аналогии для падения волны параллельной ( p ) поляризации:

U 2 ( 0 ) = ( 1 - R pp ) cos 0 ; V 2 ( 0 ) = - ( 1 + R pp ) ;

U 2 ( 1 ) = T pp cos 0 ; V 2 ( 1 ) = - T pp ;

U 1 ( 0 ) = R ps ; V 1 ( 0 ) = - R ps cos 0 ;

U 1 ( 1 ) = T ps ; V 1 ( 1 ) = - T ps cos 0 .

Системы уравнений (9) совместно с граничными условиями (12) и (13) образуют граничные задачи, решение которых позволяет определять нормированные напряженности электрического и магнитного полей в неоднородном слое кирального метаматериала. При изменении нормированного волнового числа K можно получить частотные зависимости коэффициентов отражения основной и кросс-поляризованной компонент поля от слоя кирального метаматериала. Уравнения (9) классифицируются как обыкновенные дифференциальные уравнения с переменными коэффициентами и их аналитическое решение возможно только для ряда зависимостей неоднородной функции K 0 ( C ).

Для решения дифференциальных уравнений (10) в работе используется метод дифференциальной прогонки. Будем искать решение (9) в следующем виде:

■^U 2 ( С )

. V ( С ).

= a (С)

U1 (c)

_ V 2 ( С ) _ ’

где а( С ) - неизвестная матричная функция размером 2×2.

Продифференцировав матричное соотношение (14) с учётом выражений (10) и (11), получаем матричное дифференциальное уравнение 1-го порядка относительно неизвестной нормированной координаты ^ :

d^ = -а (^) 4 (^; K) а (ф A 2 (^; K)

с начальным условием

0 - cos 0

cos 0 0

Решая уравнение (15) с граничными условиями (12) и (13), получаем соотношения для неизвестных коэффициентов отражения:

R sp

R

ss

= |^а ( о ) p + I cos 0J

cos 0

- a (0)

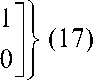
для случая оптической волны с перпендикулярной поляризацией и

R pp

R ps

= ^a(0) P+Icos0J

cos 0

+ a ( ⁰ )

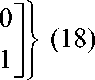
для случая оптической волны с параллельной поляризацией.

В выражениях (17) и (18) введены следующие обозначения:

1 . 1

-1

, I =

Численные результаты

В работе были рассчитаны частотные зависимости коэффициентов отражения основной и кросс-поляризованной компонент оптического поля для случая падения волн с s - и p -поляризациями.

При численном расчете были использованы две неоднородные модели кирального метаматериала:

1. Модель с линейным профилем изменения норми рованного волнового числа: K0©=Km (1 — |1 —2^|).

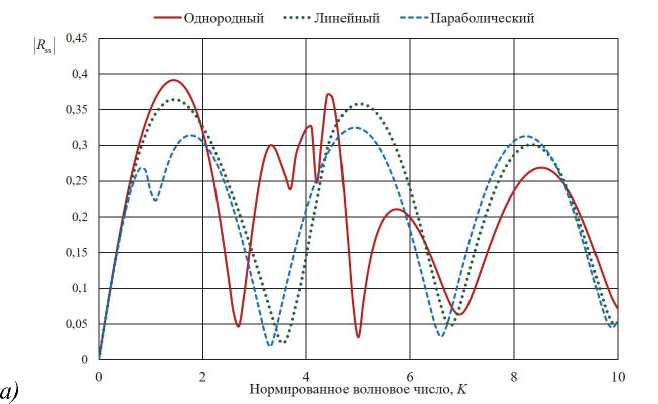
Рис. 2. Частотные зависимости модулей коэффициентов отражения основной (а) и кросс-поляризованной (б) компонент

2. Модель с параболическим профилем изменения нормированного волнового числа: K (Q = K m 4 ^ (1 - £ ).

В профилях K m – значение волнового числа на входе в неоднородный слой метаматериала.

Для сравнения были рассчитаны аналогичные частотные зависимости для случая слоя из однородного кирального метаматериала: K 0 ( ^ ) = K m .

При расчетах были использованы следующие значения физических и геометрических параметров задачи: K m = 4; K y = 0,05- K m ; 0 = n /4; s _c = 1,5-i-0,001; P c = 1 -i-0,001; Q s = 0,15; 0_Ц = 0,06; Q_v = 0,09.

На рис. 2 а , б приведены частотные зависимости модулей коэффициентов отражения основной ( R ss ) и кросс-поляризованной ( R sp ) компонент поля для случая падения волны s -поляризации.

На рис. 3 а , б приведены частотные зависимости модулей коэффициентов отражения основной ( R pp ) и кросс-поляризованной ( R ps ) компонент поля для случая падения волны p -поляризации.

Сплошными линиями показаны графики для случая однородного кирального слоя; точечными – для случая линейного профиля волнового числа; штриховыми – для случая параболического профиля.

Из рис. 2 а видно, что для случая падения оптической волны s -поляризации неоднородное распределение резонансов в слое приводит к смещению интерференционных минимумов и максимумов в частотной области. В диапазоне средних нормированных частот модуль коэффициента отражения у неоднородных слоев с параболическим и линейным профилями ниже по сравнению с однородным слоем кирального метаматериала. Аналогичные выводы можно сделать и для случая падения волны p -поляризации.

Из рис. 2 б и 3 б видно, что уровень отражения кросс-поляризованной компоненты поля одинаковый для обоих типов поляризаций падающей волны. Из графиков теоретически предсказан эффект, связанный с тем, что в области максимальной частоты резонанса неоднородные профили устраняют кроссполяризацию оптического поля (в лучшей степени неоднородный слой с параболическим профилем нормированного волнового числа).

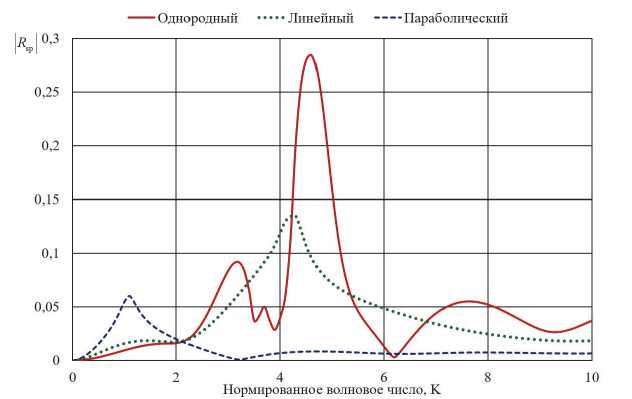
поля для случая падения волны s-поляризации

Заключение

Экспериментальное создание метаматериалов с неоднородными распределениями киральных включений может привести к разработке структур с улучшенными оптическими свойствами. Такие неоднородные структуры могут быть использованы для управления поляризацией света, создания метамате-риальных линз, фильтров и других оптических устройств с новыми функциями. Метаматериалы с неоднородными распределениями киральных элементов могут найти применение в разработке новых оптических устройств для связи и датчиков. Исследования в области метаматериалов с неоднородными распределениями киральных включений также могут привести к созданию новых устройств для обработки квантовой информации, фотонных компьютеров и других квантовых устройств.

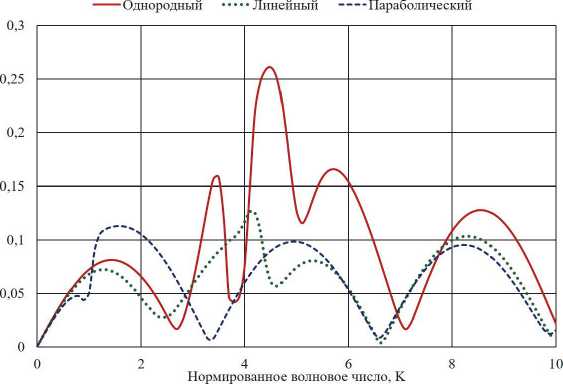
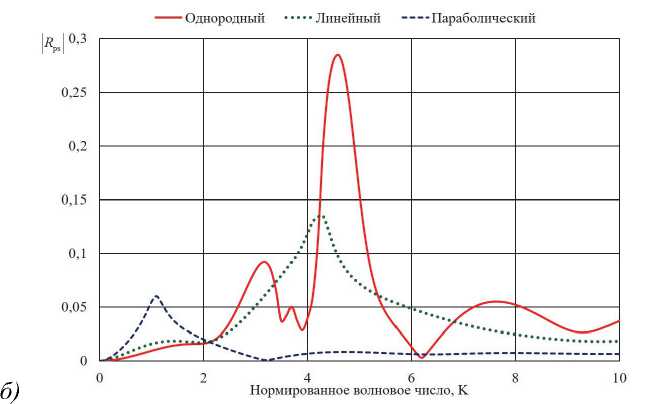
Рис. 3. Частотные зависимости модулей коэффициентов отражения основной (а) и кросс-поляризованной (б) компонент поля для случая падения волны p-поляризации

Работа выполнена при поддержке Министерства науки и высшего образования в рамках Научнообразовательного центра «Инженерия будущего» (2021 год).