Неосесимметричная динамическая задача прямогo пьезоэффекта для аксиально поляризованного сплошного цилиндра
Автор: Шляхин Д.А.
Статья в выпуске: 4, 2015 года.
Бесплатный доступ
Рассматривается неосесимметричная динамическая задача теории электроупругости для анизотропного пьезокерамического аксиально поляризованного цилиндра. Механические колебания осуществляются за счет действия на его торцевых электродированных мембранно закрепленных поверхностях нестационарной нагрузки в виде нормальных напряжений, являющихся произвольными функциями радиальной, угловой координат и времени. Разработанный алгоритм расчета позволяет удовлетворить различные механические и электрические условия на цилиндрических неэлектродированных поверхностях элемента. Для определенности в настоящей работе считаем их свободными от нормальных и касательных напряжений. Новое замкнутое решение построено в трехмерной постановке путем последовательного использования метода неполного разделения переменных в виде конечных интегральных преобразований. Последовательно применяются преобразование Фурье с конечными пределами по аксиальной координате и обобщенное конечное преобразование (КИП) по радиальной переменной. При этом на каждом этапе решения проводится процедура стандартизации, которая позволяет привести граничные условия по соответствующей координате к однородным. Полученные расчетные соотношения относительно компонент вектора перемещений и потенциала электрического поля позволяют определять частоты собственных неосесимметричных колебаний, напряженно-деформированное состояние пьезокерамического цилиндра, а также все параметры индуцируемого электрического поля. Разность потенциалов между электродированными торцевыми поверхностями определяется с помощью измерительного прибора с большим входным сопротивлением, что соответствует режиму «холостого хода». Анализ численных результатов расчета позволяет сделать вывод, что использование построенного алгоритма дает возможность по сравнению с численными методами получить более точные значения спектра частот собственных колебаний, напряженно-деформированного состояния и электрического поля пьезокерамического цилиндра.
Теория электроупругости, задача прямого пьезоэффекта, пьезокерамический цилиндр, неосесимметричная динамическая нагрузка, конечные интегральные преобразования
Короткий адрес: https://sciup.org/146211586
IDR: 146211586 | УДК: 539.3 | DOI: 10.15593/perm.mech/2015.4.14
Текст научной статьи Неосесимметричная динамическая задача прямогo пьезоэффекта для аксиально поляризованного сплошного цилиндра
Наиболее распространенными конструктивными элементами пьезокерамических преобразователей являются тела канонической формы в виде сплошных цилиндров конечных размеров (круглых толстых пластин) [1-3]. Для описания их работы в реальных условиях и расширения функциональных возможностей необходим углубленный анализ нестационарных процессов, без которого невозможно понять эффект взаимодействия механических и электрических полей напряжений. Вместе с тем существующие методы расчета пьезоэлектрических элементов конструкций на нестационарные воздействия далеко не совершенны, и большинство из них являются приближенными. При этом значительная часть исследований связана с разработкой численных методов решения [4, 5], а также с приведением этих задач к статическим или квазистатическим.
В связи с этим на первый план выходят методы, позволяющие получить замкнутые решения нестационарных начально-краевых задач теории электроупругости для тел конечных размеров в трехмерной постановке. Математические трудности при реализации данного подхода приводят к тому, что значительная часть работ в этой области связана с исследованием осесимметричных задач [6-12]. Существенно меньшее количество решений получено в случае неосесимметричной их постановки [6, 13-15]. Причем работы [6,13,14] посвящены исследованию собственных колебаний, а в [15] рассматривается установившийся режим вынужденных колебаний.
В настоящей работе неосесимметричная динамическая задача в трехмерной постановке исследуется с помощью последовательного применения конечных интегральных преобразований по всем пространственным переменным [16,17]. Данный подход позволяет получить точные, в рамках используемых моделей, расчетные соотношения в наиболее общем виде для пьезокерамического цилиндра, выполненного из материала гексагональной системы класса 6mm [18], в котором ось симметрии параллельна аксиальной координате.
1. Постановка задачи
Сплошной анизотропный цилиндр занимает в цилиндрической системе координат ( r * , 0 , z * ) область Q : | 0 < r * < b , 0 < 0 < 2 л , 0 < z * < h } и выполнен из пьезокерамического материала. Торцевые электродированные мембранно закрепленные поверхности ( z * — 0, h ) подключены к измерительному прибору с большим входным сопротивлением и загружены динамической нагрузкой (нормальными напряжениями) q 1 * ( r * , 0 , t * ) , q 2 * ( r * , 0 , t * ) , которая является произвольной функций радиальной, угловой координат и времени t * . На цилиндрических неэлектродированных поверхностях можно удовлетворить различные механические условия. Для определенности в дальнейшем будем считать их свободными от нормальных и касательных напряжений. В такой постановке задача моделирует работу пьезоэлементов в приборах прямого пьезоэффекта, трансформирующих механическое воздействие в соответствующий электрический сигнал.
Математическая формулировка рассматриваемой задачи электроупругости в безразмерной форме включает систему дифференциальных уравнений относительно компонент вектора перемещения U ( r , 0 , z , t ) , V ( r , 0 , z , t ) , W ( r , 0 , z , t ) , потенциала электрического поля ф ( r , 0 , z , t ) [6]
а т. 1av1. aw аф ,
(1.2)
z = 0, L: ° zzz =0 = a111 V U + l + a7^ + ^ = Q1 ( r, 0- t ) ,
V r a0) a z a z
° zz | z = L = a 11
1 av ) aw aф
( r , 0 , t ) ,
VU + + a7-- + — q7
r a0) 7 az az 2
U ( r , 6 ,0, t ) — U ( r , 6 , L , t ) = 0, V ( r , 6 ,0, t ) = V ( r , 6 , L , t ) = 0,
D z I z = 0, L
°M„ a 10 ~ + a 12 8 z
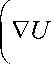
1 8 V A 8 W
+---+--— r 8r J 8z
0;
8 U 8 V 8 W 8ф 8 U 8 V 8 W 8ф
6 — 0,2 л : UU , V , W , ф,--- , —, , — U , V , W , ф,--- , —, , , (1.3)
I 86 86 86 86j|0 0 I 86 86 86 86 J|0 27I„
8U 1 f 8VA 8W 8ф r = 1,0: CTrr । r—1 = "Г + a13 — I U + I + a11 ~ + а12Д2"" = 0,
8 r r V 86 J 8 z 8 z
(1.4)
<8 W 8 U A 8ф _
CT rzIr — 1 = a 2 I ~; + “T- I+ a 8 T- = 0 , CT r 6| r —1 = a 1
V 8 r 8 z J 8 r
D r — 1
8Ф .
— - a 9 — + a 8 8 r
1 <8 U 8 V'
-I--v I + — r V 86 J 8r
< 8 W 8 U A _ —+— I— 0,
V 8 r 8 z J
— 0,
U ( 0, 6 , z , t ) <ю , V ( 0, 6 , z , t ) <да , W ( 0, 6 , z , t ) <« , ф ( 0, 6 , z , t ) <»;
t — 0: U ( r , 6 , z ,0 ) — U 0, V ( r , 6 , z ,0 ) — V 0, W ( r , 6 , z ,0 ) — W 0, U ( r , 6 , z ,0 ) — U 0, V ( r , 6 , z ,0 ) — V 0, W ( r , 6 , z ,0 ) — W 0, где ( U , V , W } — { U *, V *, W *} / b , ф — ф * e33^bC11 ) , { r , z , L } — { r * , z , , h } / b ;
(1.5)
t — t * b -1 Т с ЦТр' , V ? —
8 2 1 8 1
—т +-----T,
8 r 2 r 8 r r 2
v 2 — v 2 + 4, V ——+^; r 2 8 r r
{ a 1 ,a 2 , ^ 3 , a 4 , a 5 , a 7, au,a 13 } — { C 66, C 55 , ( C 12 + C 66 ) , ( C n + C 66 ) , ( C 13 + C 55 ) , С зз , C 13 , C 12}/ Cn ;
{ a 6 , a 8 , a 12 } — {( e 31 + e 15 ) , e 15 , e 31}/ e 33 , { a 9 , a 10 } — { C 11 e 11 , C 11 S 33}/ e 33 ^
{q 1, q2} —{q 1*, q2*}/c11 ; CTjk, Dm - соответственно компоненты тензора механических напряжений и вектора индукции электрического поля (j, k — r, 6, z; m — r, z); b - радиус цилиндра; p, Cms, ems - объемная плотность, упругие постоянные и пьезомодули анизотропного пьезокерамического материала ( m, s — 1,6); е11,833 - диэлектрические проницаемости в радиальном и осевом направлениях; U*, V*, W*, ф* — компоненты вектора перемещений и потенциал электрического поля в размерной форме; U0,U0, V0, V0,, W0, W0 — известные в начальный момент времени перемещения, скорости перемещений.
Электрические граничные условия (1.2), (1.4) соответствуют режиму «холостого хода» на торцевых поверхностях и отсутствию электродного покрытия на цилиндрической поверхности цилиндра. Соотношения (1.3), (1.4) ( r — 0) являются условиями периодичности для круговых областей и регулярности решения. Начальные условия (1.5) определяет деформированное состояние системы в момент времени t — 0.
В равенствах (1.5) и ниже точка означает дифференцирование по t .
2. Построение общего решения
Решение осуществляется методом интегральных преобразований, путем последовательно синус- и косинус-преобразования Фурье с конечными пределами по переменной О и z [19], а также обобщенного конечного преобразования (КИП) [20] по радиальной координате r . При этом каждый раз предварительно необходимо выполнять процедуру стандартизации (приведение граничных условий по соответствующей координате к однородным). На первом этапе для этой цели используется такое представление:
{ U ( r , О , z , t ) , V ( r , О , z , t ) } = H i ( r , О , z , t ) + { u ( r , О , z , t ) , v ( r , О , z , t ) } ,
W ( r , 0 , z , t ) = H 2 ( r , 0 , z , t ) + w ( r , 0 , z , t ) , ф ( r , О , z , t ) = H 3 ( r , О , z , t ) + % ( r , 0 , z , t ) .
Здесь H 1 = ( Lz - z 2 ) ( q 1 + q 2 ) , H 3 = a 9 1 H 2,
H 2 = a 9 [ 2 L ( a10 - 1 ) ] Г ( 2 Lz - z 2 - L 2) q , + z 2 q 2
В результате подстановки (2.1) в (1.1)-(1.5) получаем новую краевую задачу относительно функций u ( r , 0 , z , t ) , v ( r , 0 , z , t ) , w ( r , 0 , z , t ) , % ( r , 0 , z , t ) с однородными граничными условиями по координатам z и 0 . При этом дифференциальные уравнения (1.1), граничные условия (1.4) становятся неоднородными с правыми частями F 1 + F 4 и N 1 ^ N 4, а в начальных условиях (1.5) вместо U 0, V0, W0 следует принять u 0, v 0, w 0.
К преобразованной краевой задаче (1.1)-(1.5) применяем последовательно синус -и косинус-преобразования Фурье с конечными пределами по переменной z и 0 , используя следующие трансформанты:
-
{ w ( r , 0 , n , t ) , vs ( r , 0 , n , t ) } = £ { u ( r , 0 , z , t ) , v ( r , 0 , z , t ) } sin ( jnz ) dz , { w c ( r , 0 , n , t ) , % c ( r , 0 , n , t ) } = £ { w ( r , 0 , z , t ) , % ( r , 0 , z , t ) } cos ( j n z ) dz , { Uc ( r , m , n , t ) , W c ( r , m , n , t ) , ф c ( r , m , n , t ) } =
(2.2)
(2.3)
= £ q2" { u s ( r , 0 , n , t ) , w c ( r , 0 , n , t ) , % c ( r , 0 , n , t ) } cos ( m 0 ) d 0
Vs (r, m, n, t) = £2" vs (r, 0, n, t) sin (m0) d0, с соответствующими формулами обращения
{us ( r, 0, n, t) , ws ( r, 0, n, t) , %s ( r, 0, n, t)} = to
= ^ P m { U c ( r , m , n , t ) , W c ( r , m , n , t ) , ф c ( r , m , n , t ) } cos ( m 0 ) , m = 0
to vs (r, 0, n, t) = л-1 ^ Vs (r, m, n, t) sin (m0), m=1
№
{ w (r, 0, z, t) , X(r, 0, z, t)} = EQ^ {wc (r, 0, n, t), %c (r, 0, n, t)} C0S jnz , n=0
/ = nn IL, P nm
2 л
к
( m = 0), Q f L ( « = 0),
( m ^ 0), n [L /2 ( n ^ 0).
В результате получаем следующую начально-краевую задачу относительно трансформант Фурье Uc ( r , m , n , t ) , V s ( r , m , n , t ) , W c ( r , m , n , t ) , ф c ( r , m , n , t ) :
v 2n m .2 m 8V s m . 8W c . 8ф c S U c
(2.4)
V1 Uc “ a1 ~Uc ~ a2 JnUc + a3--Д--a4 — Vs ~ a5Jn -;--a6Jn У---У~ = R1 c , r r 8 r r 8 r 8 r 81
V72V m2 -2T/ a1V1 Vs--F Vs “ a2 JnVs - a3У r r8
^^^^H
mmm a4 —Uc + a5Jn — Wc + a6 Jn - ф, rrr
r
8!i^=r c 812 R2 s'
. I m т У a5j V U + V + аг
5 n c s
V 2 W c
V
^^^^^^^s
2 A m F W c r J
^^^^^^^s
I a 7 J nWc + a 8 V 2 ф.
^^^^^^^s
I m a6 Jn I V Uc + —Vs l + a8
a 2
V W
^^^^^^^e
' V r = 1 o • 8 Uc +a
* , : I a l
8 r
2 m F W c r J
nc
V
I a 9 V 2 ф,
V
m2
— ф c r J
^^^^^^^s
j n 2 Ф c
^^^^^^^s
8 2 Wc. „
2 = R
^^^^^^^e
m . 2
— ф c + a10 JnФ c = R r J
- 4 c ’
1 ( U c + mV s ) - a ll j n W c - a i2 j n ф c = Y 1 cr = 1 ,
(2.5)
(6W А Эф
-W + J n U c l + a 8 Ff- = Y 2 cr = 1 , a
V 8r J 8r
8 Vs
8 r
■1 (mUc + Vs) = Y3
r
3 s | r = 1 ,
8ф c
19 д + a 8 8 r
(8W )
-Wc + J n U c l = Y 4 dr = 1 ,
V 8r J
।, m, n,t )<№ , Vs ( 0,m, n, t )<№, Wc (0, m, n, t )<да , ф c (0, m, n, t ) (2.6) Vs (r, m, n,0) = V0s (r, m, n), Vs (r, m, n,0) = V0s (r, m, n), Wc (r, m, n,0) = W0c (r, m, n), Wc (r, m, n,0) = W0c (r, m, n), где {R1 c, R3 c, R 4 c, Y1 c, Y2 c, Y4 c, U0 c, U0 c, W0 c, W0 c } = = J02"^ F1 s , F3c , F4c , N1 s , N2c , N4c , u0s , Ul0s , w0c , ^0c } cos(m0) d0 {R2s , Y3s , V0s , V0s } = {(L {F2s , N3s , v0s , V0s } sin(m0) d0, {F1 s , F2 s , N1 s , N3 s , u 0 s , U0 s , v0 s , V0 s } = j^ { F1, F2, N1, N3, u 0, Vf v0, V0 } sin ( Jnz ) dz , {F3c , F4c , N2c , N4c , w0c , ^w0c } = j^ {F3, F4, N2, N4, w0, ^w0 } C0S( Jnz ) dz . Повторяя еще раз процедуру стандартизации задачи (2.4)-(2.6), представляем трансформанты Фурье Uc, Vs, Wc, фc в виде Uc ( r, m, n, t) = H4( r, m, n, t) + UC (r, m, n, t), Vs (r, m, n, t ) = H5(r, m, n, t) + Vs*( r, m, n, t), Wc (r, m, n, t) = H6 (r, m, n, t) + Wc* (r, m, n, t), фc (r, m, n, t) = H7(r, m, n, t) + фС (r, m, n, t), ГдеH4 =(r—1)Y । r=1, H5 = a1 ( r —^ Y3 s|r=1, H6 = a 2 (r—1)(Y2 c | r=1 —a8Y c|r=1 )’ H7 =(r— 1 Y5 c I r=1’ Y5 c I r=1 = a8 ( a 2 a9 +a 8 ) ( Y4 c I r=1 —a 2 a 8 Y2 c I r=1 ) . При подстановке (2.7) в (2.4)-(2.6) получаем краевую задачу относительно функций Uc, Vs, WC, фС с однородными граничными условиями по координате r. При этом вместо правых частей дифференциальных уравнений (2.4) R1c,R2s R3c, R4c и начальных условий (2.6) U0c, (j0c, Vos, V>0s, Woc, Woc следует принять R^, R2s, R3c, R2c и U0c, U>' , VCS, V^CS, W0*c, WC. Краевую задачу (2.4)-(2.6) относительно функций UC, Vs*, Wc*, фС решаем, используя структурный алгоритм обобщенного метода конечных интегральных преобразований (КИП) [20]. Введем на сегменте [0,1] вырожденное КИП с неизвестными компонентами K1 ( ^in. ’ r ) ’ K2 (^,nm . r ) ’ K3 (^inm ’ r) ’K4 (^inm ’ r) ВекТОр-функциИ ядра прбобразования G (^inm, m, n, t) = /0(UC K1 + v;K2 + WCK3)rdr, (2.8) w {u;,v;,w;,фС} = £g(K1,к,,к3,к4}||к„„|Г , (2.9) i=1 I Kinml I2 =/0[ к ,2+к 2+к3 ] rdr, где Xinm - положительные параметры, образующие счетное множество (i = 1, w). При этом круговые частоты неосесимметричных колебаний цилиндра toinm связаны с Xinm зависимостью ®,nm =Xnmb—V^P . (2.10) Подвергая систему уравнений и условия вида (2.4)-(2.6) относительно функций UCC, Vs, Wc, фС преобразованиям в соответствии со структурным алгоритмом [20], получаем счетное множество задач Коши для трансформанты G (Xinm, m, n, t), решение которых имеет вид G(X„m ’ m ’ n ’ t)= G0CPS (X„mt) +0S.n (X„mt)/ Xnm—Xinm {.F(X„m ’ m ’ n ’ t Ц (2.11) X Sln Xinm (t — T) dV и однородную краевую задачу для компонент К1 ^ К4: V7 2 m2 ■ 2 , Л 2 A I m d m L . dK3 . dK4 A V1 a a2Jn +Xinm К 1 +1 a3 a4 IK2 a5Jn a6Jn - 0, (2-12) r v r dr r ) dr dr 2 aiVi v m , 2 . л 2 —т--67 э 7 “FA- lx.о 2 2V n mm 2 ^^^^^^^^ a 3 V md rdr m I m m +a4 — IK1 +a5Jn —K3 +a6Jn —K4 - 0 , r ) r r r a 5 jn V К 1 + — К2 I + r V a6 jn a 2 V 2 v m 2 a7 jn + X inm r ) К3+ a8 V m ^^^^^^^. j n К4- 0, v V К1 + — К2I + r ) a 8 V2 v ^^^^^^^. m r 2 v ^^^^^^^. К3 ^^^^^^^. ^^^^^^^. V r2 I a9 V2 К 4 - 0, dK r - 1 : -Д- + a13 (К1 + mK2 )- all JnK3 - ai2 JnK4 - 0 , dr (2.13) dK3 dr + JK 1 - 0, d^ - 0 dr d^ - —к - К - 0, dr 1 2 ’ r - 0 : K1 < да, К2< да, К3< да , К4< да. ЗдеСЬ F (Xin— , m, n, t) -J01[R1sK 1 +R2*cK2 +R3*sK3 +R4*sK4 ] rdr, G0 (Xin—, m, n) j [U0cK1 + V;SK2 + W*.cK3 ] rdr, G?0 (Xinm , m, n)- Л [ц/0cK1 + V;SK2 + W0cK3 ] rdr. При исследовании системы (2.12) имеют место следующие случаи: m - 0 и m ^ 0. Когда m - 0, рассматривается осесимметричная задача, решение которой получено автором в работе [7]. Для решения (2.12) при m ^ 0 вводятся новые функции К5, К6 на основании следующих представлений: К5 - rsK,, К6 - r-K,. (s =±1). (2.14) Тогда частные решения системы дифференциальных уравнений (2.12) находятся методом разложения функций К3^ К6 в следующие степенные ряды: {К3,К4,К5,К6}-r₽ jr {Ef,Rf,Yf,Pf}rf. (3-const). (2.15) f -0,2,4 После подстановки (2.15) в (2.12) приравниваем нулю все множители с одинаковой степенью и получаем значения для параметра 0 , а также выражения для коэффициентов Ef, Rf, Yf, Pf. В результате получаем четыре линейно независимых частных решений. Подстановка полученных соотношений для К1 ^ К4 в граничные условия при r - 1 (2.13) формирует однородную систему уравнений относительно постоянных D1 ^D4. Ра- зыскивая ее нетривиальное решение, получаем трансцендентное уравнение для вычисления собственных значений X inm, а также выражения для D1 ^ D4. При этом полученные выражения для K1 ^ K4 удовлетворяют также и условия регулярности решения в центре пластины (краевые условия (2.13) при r = 0). Применяя к трансформанте (2.11) последовательно формулы обращения (2.9), (2.3), (2.2), получаем с учетом (2.1), (2.7) следующие разложения для U(r,0,z,t), V(r,0,z,t), W(r,0,z,t), ф(r,0,z,t): 3 to toto cos (m0) f sin jnz, (2.16) sin (m0) f sin jnz, u(r,0,z,t) = h 1 + -XXP- h4 ■ XGK11IKmII L n=1 ^ m=0 _ 3 to toto V (r, 0, z, t) = H1 ■ - X Л X H5 + X GK21Kn. II L n=1 ^ m =1 _ toto to H6 + X GKз| IKJ i=1 to H7 + X GK4 KJ i=1 cos (m 0)>cos jnz cos (m0)f cos jnz . W (r, 0, z, t ) = H, + Xn -1 IX P-1 n=0 toto ф( r, 0, z, t ) = H3+Xn -1IX Pm; n=0 Разность потенциалов Q (t*) между торцевыми электродированными плоскостями пьезокерамического цилиндра определяется с помощью следующего равенства: 12л а Q (t *) = (л а2) Jj[v( r*, 0, L, t *)-ф( r*, 0,0, t *)]r* dr. d 0. 0 0
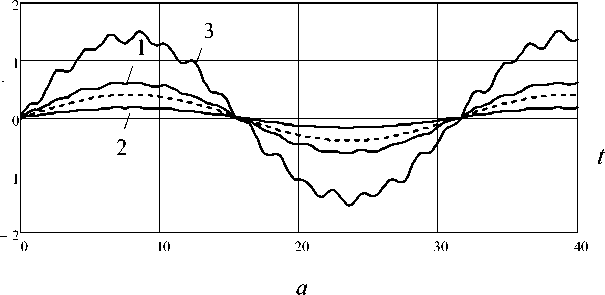
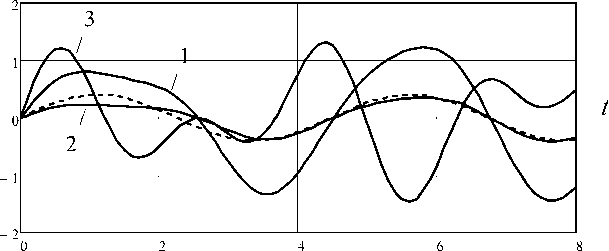
3. Численный анализ результатов. Выводы В качестве примера рассматривается пьезокерамический цилиндр ( b = h = 0,01 м) состава ЦТС-19, имеющего следующие физические характеристики материала: {e31, e33, e15} = = {-3,7;11,5;10,3}Кл/м2, {еи,£33} = {8,08; 7,73}х10-9 Ф/м, {Cn,C12,C13,C33,C55,C66} = = {13,2; 6,2; 6,9; 10,4; 2,8; 3,5}х 1010Н/м2, р = 7400 кг/м3. В таблице приведены численные значения спектра частот собственных колебаний щinm (m = 0,1,2, n, i = 1,2,3) пьезокерамического цилиндра, полученные с помощью построенного в настоящей работе алгоритма (верхние числа) и численным методом конечных элементов с использование программы ANSYS (нижние числа). Следует отметить, что наименьшее расхождение численных значений toinm наблюдается при вычислении первого тона (i = 1) колебаний. Вместе с тем с ростом i разница в частотах, найденных аналитическим и численным методами, становится более существенной и достигает 9,8 %. Кроме того, интересно отметить, что первая частота собственных неосесимметричных колебаний соответствует образованию одной полуволны по угловой координате (m = 1) и вдоль цилиндрической поверхности (n = 1) исследуемого элемента. Значения спектра частот собственных колебаний пьезокерамического цилиндра ^ inm , кГц m = 0 m = 1 m = 2 n = 1 n = 2 n = 3 n = 1 n = 2 n = 3 n = 1 n = 2 n = 3 i = 1 113,4 108,1 257,2 317,9 77,2 165,5 251,6 92,8 169,6 252,5 242,4 294,3 74,9 159,1 239,6 89,2 161,5 240,0 i = 2 187,2 176,6 344,3 324,8 396,5 370,6 117,5 114,1 190,6 183,2 273,1 260,1 145,2 138,3 209,2 195,5 285,5 264,3 i = 3 226,9 214,0 434,5 485,1 158,7 214,1 287,5 195,1 247,1 315,7 402,2 445,0 151,1 201,9 268,7 182,2 228,7 287,2 На рисунке приведены графики изменения вертикальных перемещений W (r, 0, z, t) и разности потенциалов Q (t) во времени в случае действия на половине торцевой поверхности цилиндра (0 < r< 1, 0 < 0 < л) равномерно-распределенной нагрузки интенсивностью q0 и различной частоты ц : q1 (r, 0, t) = q1 (r, 0, t) = q0H (л - 0) sin цt, где H (...)- единичная функция Хэвисайда [21]. {W ( r, 0, L, t) ,Q (t)} / q 0 {W ( r, 0, L, t) ,Q (t)} / q 0 Рис. Графики изменения W(r,0,z,t) и Q(t) во времени: a - ц = 0,21 inm (i,n,m = 1); 6- ц = 0,71^ (i,n,m = 1); 1 - W(1, л/2,0,t); 2 - W(1,3л/2,0,t); 3 - Q(t) Цифрами 1, 2, 3 соответственно обозначены функции W(1,л/2,0,t), W(1,3л/2,0,t), Q (t), а пунктирной линией показан характер изменения внешней нагрузки во времени. Очевидно, что вертикальная компонента вектора перемещений на незагруженном участке при 0 = 3 л/2 существенно меньше соответствующих значений в зоне действия нагрузки при 0 = л/2. Результаты расчета также показывают, что при действии гармонической нагрузки допущение о стационарном режиме вынужденных колебаний, используемое при исследовании динамических задач, справедливо только в случае, когда частоты вынужденных колебаний существенно меньше первой частоты собственных колебаний. При высокочастотном внешнем воздействии вследствие наложения отраженных волн деформирования наблюдается более сложная зависимость изменения напряженно-деформированного состояния и электрического поля системы во времени. На основании проведенных исследований можно сформулировать основные результаты. 1. Построено новое замкнутое решение, позволяющее с помощью базовых расчетных соотношений описать работу типовых элементов пьезокерамических преобразователей резонансного и нерезонансного классов в виде сплошного цилиндра, подверженных действию динамической неосесимметричной механической нагрузки. 2. Численные результаты расчета показывают, что использование построенного алгоритма расчета позволяет, по сравнению с численными методами, получить более точные значения спектра частот собственных колебаний, напряженно-деформированного состояния и электрического поля пьезокерамического цилиндра. 3. В случае действия высокочастотной внешней гармонической нагрузки при исследовании упругих и электроупругих систем нельзя использовать допущение об установившемся режиме вынужденных колебаний.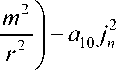
Список литературы Неосесимметричная динамическая задача прямогo пьезоэффекта для аксиально поляризованного сплошного цилиндра
- Данов Г.А. Пьезоэлектрические трансформаторы. -М.: Энергоатомиздат, 2003. -319 с.
- Джагупов Р.Г., Ерофеев А.А. Пьезоэлектронные устройства вычислительной техники, систем контроля и управления. -СПб.: Политехника, 1994. -608 c.
- Пьезоэлектрическое приборостроение. Т. 1. Физика сегнетоэлектрической керамики/А.В. Гориш . -М., 1999. -386 с.
- Шульга Н.А. Болкисев А.М. Колебания пьезоэлектрических тел. -Киев: Наук. думка, 1990. -228 с.
- Блочные схемы метода конечных элементов для динамических задач акустоэлектроупругости/А.В. Белоконь //ПММ. -2000. -Т. 64, № 3. -С. 381-393.
- Гринченко В.Т., Улитко А.Ф., Шульга Н.А. Механика связанных полей в элементах конструкций. -Киев: Наук. думка, 1989. -279 с.
- Сеницкий Ю.Э. Шляхин Д.А. Нестационарная осесимметричная задача электроупругости для толстой круглой анизотропной пьезокерамической пластины//Изв. РАН. МТТ. -1999. -№ 1. -С. 78-87.
- Шляхин Д.А. Нестационарная осесимметричная задача электроупругости для анизотропного пьезокерамического радиально поляризованного цилиндра//Изв. РАН. МТТ. -2009. -№ 1. -С. 73-81.
- Шульга М.О. Определение электродвижущей силы пьезоэлектрических преобразователей при механических нагрузках//Докл. НАН Украины. -2009. -№ 1. -С. 70-74.
- Шульга Н.А. Радиальные электромеханические нестационарные колебания полого пьезокерамического цилиндра при электрическом возбуждении//Прикладная механика. -2009. -Т. 45, № 2. -С. 30-35.
- Quan Jiang, Cun-Fa Gao. Axisymmetric stress in an electrostrictive hollow cylinder under electric loading//Acta Mechanica. -2010. -Vol. 211. -Iss. 3-4. -Р. 309-321.
- Wang Y., Xu R.Q., Ding H.J. Analytical solutions of functionally graded piezoelectric circular plates subjected to axisymmetric loads//Acta Mechanica. -2010. -Vol. 215. -Iss. 1-4. -P. 287-305.
- Лоза И.А. Решение задачи о неосесимметричных колебаниях полых пьезокерамических цилиндров конечной длины//Докл. НАН Украины. -2010. -№ 6. -С. 52-58.
- Григоренко А.А., Лоза И.А. О свободных неосесимметричных колебаниях полых пьезокерамических цилиндров конечной длины с радиальной поляризацией//Прикладная механика. -2010. -Т. 46, № 11. -С. 20-30.
- Лоза И.А. Неосесимметричные колебания полого неоднородного шара с пьезокерамическими слоями//Докл. НАН Украины. -2011. -№ 11. -С. 76-83.
- Сеницкий Ю.Э. Метод конечных интегральных преобразований. Его перспективы в исследовании краевых задач механики//Вестник Сарат. гос. техн. ун-та. Серия математическая. -2003. -Вып. 2. -С. 10-39.
- Сеницкий Ю.Э. Метод конечных интегральных преобразований -обобщение классической процедуры разложения по собственным векторам-функциям//Изв. Саратов. ун-та. Новая серия. Математика, механика, информатика. -2011. -№ 3(1). -С. 61-89.
- Партон, В.З., Кудрявцев Б.А. Электроупругость пьезоэлектрических и электропроводных тел. -М.: Наука, 1988. -470 с.
- Снеддон И.Н. Преобразования Фурье. -М.: Изд-во иностр. лит., 1955. -668 с.
- Сеницкий Ю.Э. Многокомпонентное обобщенное конечное интегральное преобразование и его приложение к нестационарным задачам механики//Изв. вузов. Математика. -1991. -№ 4. -С. 57-63.
- Владимиров В.С. Обобщенные функции в математической физике. -М.: Наука, 1978. -318 с.


