Непараксиальная векторная дифракция гауссового пучка на спиральной фазовой пластинке

В современных научных исследованиях изучение вихревых лазерных пучков является важной частью сингулярной оптики [1]. Основные причины возросшего интереса к таким пучкам заключаются в возможности решения с их помощью прикладных задач [2-6].

Вихревые лазерные пучки формируются при прохождении света через спиральные оптические элементы, простейшими из которых являются спиральная фазовая пластинка (СФП) и спиральный аксикон [7].

Существует множество работ, посвященных анализу дифракции света на спиральных оптических элементах, выполненных в рамках скалярной теории дифракции. В данной работе проводится анализ векторной дифракции гауссового пучка на СФП без использования параксиального приближения. В [8] численно показано, что в ряде случаев заметный вклад дает продольная составляющая электрического вектора, не учитываемая в скалярной теории. Поэтому в данной работе получены аналитические выражения также и для продольной составляющей поля.

1. Интегральные преобразования, описывающие распространение вихревых лазерных пучков в свободном пространстве

Известно, что распространение света в свободном пространстве описывается дифракционными интегралами Рэлея-Зоммерфельда [9, 10]:

Er (u, v, z) =--x xV 7     2n где R = l(u -x) +(v-y) + z2 I , (x,y) - декартовы координаты в плоскости СФП z = 0, (u, v) - декартовы координаты в плоскости, отстоящей на расстоянии z от плоскости СФП, к = 2п/Л - волновое число, λ – длина волны.

При вычислении этих интегралов множители, содержащие производные от функции R ^{- 1} exp ( ikR ) , обычно заменяют приближенными выражениями. При параксиальном приближении это делают следующим образом: в показателе быстро осциллирующих экспонент делают замену

2 z

а в остальных случаях полагают R ® z . После этих преобразований вместо (1) получатся следующие выражения:

E xy ( ^u , ^v , ^z ) ~ ^- ;7 k - exp ( ^ikz )^x

2nz xJJ Ex, y (x, y,0) exp { i7 x

R 1^{2 z}

E z ( u , v , z ) - 2 i n z 2- exp ( ikz ) x

• xJJE(x - u) Ex (x, y ,0)+( y- v) Ey (x, y ,0)Jx

R ²

x exp

^E y ( ^U , ^V , ^Z ) = -

— x

2n

^X JJ E y ^{( x} , y ,⁰⁾f

2 z

exp ( ikR )!

---R —- d x d y ,

^E z ⁽ u , ^V , z ) =     JJ { E x ^{( x} , y ,^{0 )}£

2 П 2                 ХЛ.

R

exp ( ikR )

R

. у _m d exp ( IkR )

⁺ E x ( ^x , y ^,0h--' r^{d x d} y ^, 8y    ^R

где E_{x , y} – это либо E_x , либо E_y . Из формулы (3) видно, что для поперечных составляющих получается известное преобразование Френеля. В [11] используется менее грубая аппроксимация: в показателе быстро осциллирующих экспонент делают замену

R - uu + v + z + f         —,        (4)

а в остальных случаях полагают

R ® ( u ² + v ² + z ² ) ¹² . После этих преобразований вместо (1) можно приближенно записать:

ikz exp ( ik^u ² + v ² + z ² )

E   ( u , ^V ’ z ) ” ,7           2X ----^X

2 n ( u + v + z )

^x JJ E x.y ( x , У ,0 ) exp

R ²

x ( x ² + y ²

ik

—i        x

2 V u ² + v ² + z у

- 2 ux - 2 vy ) J d x d y ,

<

E z ( u , v , z ) » —    ik ---— exp ( iMu² + v ² + z z

2 n ( u ² + v ² + z ² )     '

^x JJ [ ( x - и ) E x ( x , y ,0 ) ⁺ ( y ^{- v} ) E y ( x , y ,0 ) ] ^x R ²

)X

x exp

x exp

ik

2 V u ² + v²

ik

( x ² + y ² )

x

( ux + vy ) d x d y .

Можно заметить, что при ( u + v ) « z фор-

мула (5) преобразуется в (3).

В случае, когда пучок во входной имеет вихревую составляющую, т. е.

[ E x ( r , ф ,0 ) = A x ( r ) exp ( in ф ) ,

[ E y ( r , ф , 0 ) ^ A y ( r ) exp ( in ф ) ,

плоскости

где ( r , ф ) - полярные координаты в плоскости

z = 0 , двойные интегралы в (3) и (5) после перехода

kz exp ( in 9 + ik Jp ² + z ² ) E x , y ( p,9, z ) = ( - i ) n + ¹-------(-^r^^.

к полярным координатам могут быть сведены к одинарным.

В случае параксиального приближения (3) получаются следующие выражения:

,    ( _      \        A n ^{+1 k} „ I ^{ik P} . - A . I

Ex(p,0,z) = (-г)  —exp--+ in9 + ikz x x ’y v           x ’ z V 2 z                J

x

^E z ( p, ⁹, ^z ) = ( ^- i ) ' ^k exp z

, I k p r I д J „ \ -----I r d r ,

V z J ikP2 , - Q )

--+ in9 + ikz Ix

2 z             J

<

x "expfzeHAx(r)-iAy(r)eXnfi x exp(i0)j        2 expI

T f k p r I ₂          , .

x J n + i I---- I r d r - exp ( - г 9 ) x

V z J r Ax (r) + iAy (r)    I ikr2 \ xJ--------p        Jn-i о 2           V 2 z J

r

- i pj|^ A_x ( r ) cos9 + A_y ( r ) sin9]^x

x exp

,

x

r ²d r -

где ( p , 9 ) - полярные координаты в плоскости, отстоящей на расстоянии z от плоскости СФП, J_n ( x ) – функция Бесселя первого рода n -го порядка.

В случае непараксиального приближения (5) получаются похожие, но более точные выражения:

r

J A_{x y} ( r ) exp

ikr

z

T I ^k p ^r

^J n I / 2      2

U/p + z J

r d r ,

in 0 ) x

E z ( p , 9, z ) = ( - i ) n k exp ( ik p² + z ² + ^x ' ^x ' p + z \

r A x ( r )- iA y ( r )_„f    ikr 2	I	k p r
exp ( i 9) J            2              pl T / 2 , 2 0         2            V 2 Np + z J	J n + 1 I	22 V p + z j

A x ( ^r )⁺ iA y ( ^r )      f ikr у

--—---^y--z- exp I —,

²             V 2 V p² + z² ,

J n-1

k p r

V p2 + z у r 2d r -

- exp ( - i 9 ) J

rr./\    „                  I     ikr²

-ipJ[Ax (r)cos 9 + A, (r ) sin 9 J exp I — о                                  V2Vp2+z

2. Аналитические выражения для векторной дифракции гауссового пучка на спиральной фазовой пластинке

Если на СФП падает гауссов пучок, т. е. A_xy ( r ) = B_xy exp ( - r ²/ w ² ) , то интегралы в выражениях (7) и (8) можно вычислить с помощью следующего справочного интеграла [12]:

J n

k p r

V p ² + z у

r d r

r

J exp ( - px ² ) J_v ( cx ) x d x =

I v - 1 ( y )^- I v +1 ( y )

= 8p 2 ^6xp<" ^y >

Re v >-2,

где y = c2/(8p), In (x) - функция Бесселя второго рода, и с помощью еще одного интеграла, который можно получить из (9):

ад j exp (-px2) Jv ( cx ) x2dx =

^exp ( - y ) { ( v + 2 - 3 y ) x 8 p

I.(y)- L+y(y)

⁺ y I v-l ( y )^- I v +4 ( y )

>

После применения интегралов (9) и (10) к выражениям (8) получим:

B kz exp in 0 + ikdp ²

E x , y ( p, 0, z ) = ( - i ) n + 1 - y ------L^ - 2-----

⁺ z ) c Я , _x ----8"^ exp ( - y )

I n - i ( y ) ^- I n + i ( y )

E z ( P, M = ( - i )"

k p2 + z 1

exp ( ^ik ^ p ^{2 + z 2 +} in ⁰ ) 8 p |_r exp ( ^- y ) ^x

B_x - B

V

exp ( i 0 ) < ( n + 3 - 3 y )

I n + 1 ( y ) ^- I n + 3 ( y ) ⁺ y I n^ ( y ) ^- I n + 5 ( y )

2               2 J L 2               2        .

-

B_x + iB)

^exp ( ^- i ⁰ )u ^{n +}1^{- 3} y ) I n -1 ( y ) ^- I n + 1 ( y ) ⁺ y I n - 3 ( y ) ^- I n + 3 ( y ) >

-

X

- i ( B_x cos 0 + B y sin

⁰ ) ^c p I n _i ( y ) ^- I n + 1 ( y )

-17

В уравнении (11) приняты обозначения:

1 ik               k p            c c

-2"-- 1        , c = .        , y = —.

w 27 p² + z²       7 p² + z^{2       8} p

Декартовы составляющие вектора напряженности электрического поля (11) описывают в цилиндрических координатах непараксиальную дифракцию Гауссового пучка на СФП с топологическим зарядом n . Заметим, что при B x = ± iB_y Гауссовый пучок имеет круговую поляризацию, а например при B_x ^ 0 , B y = 0 - линейную поляризацию.

• (11) для параксиального приближения. Таким образом, было проверено полученное выражение (10).

Затем было проведено численное сравнение параксиального приближения (7) и более точного непараксиального приближения (8). Результаты моделирования приведены на рис. 1. Были использованы следующие значения параметров: длина волны X = 633 нм; радиус перетяжки Гауссового пучка w = 1 мкм; порядок СФП n = 3 ; расстояние вдоль оптической оси z = 10 мм; амплитуды составляющих Гауссового пучка B x = 1 и B y = 0,2 i (эллиптическая поляризация).

Из рис. 1 видно, что поперечные составляющие вектора напряженности электрического поля, полученные с помощью параксиального и непараксиального приближений, отличаются друг от друга (максимальная ошибка составляла 14%). Продольная составляющая в данном случае мала.

(а)

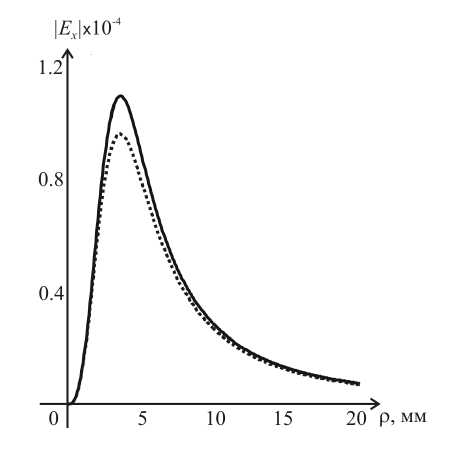
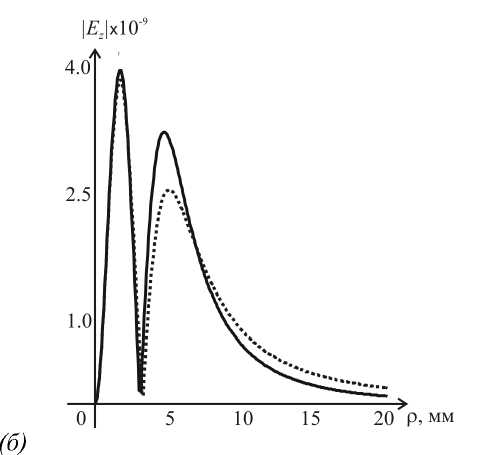
Рис. 1. Дифракция гауссового пучка на СФП: поперечная составляющая E_x (а) и продольная составляющая E_z (б) (сплошная кривая – в параксиальном приближении, пунктирная – в непараксиальном)

На рис. 2 показана дифракция того же гауссового пучка, но на расстоянии z = 10 мкм.

Из рис. 2 видно, что при таких условиях уже следует учитывать влияние на интенсивность продольной проекции вектора электрического поля, так как она составляет примерно 3% от поперечной.

На рис. 3 показано радиальное распределение модуля напряженности электрического вектора, по- лученное по формуле (11) (сплошная кривая) и с помощью дифракционного интеграла Рэлея-Зоммерфельда (1) (в виду трудоемкости вычислений значения показаны отдельными точками). Параметры расчета имеют те же значения, что и для рис. 1 и 2. Расстояние было принято равным z = 10 мкм.

Из рис. 3 видно, что формула (11) дает результаты, практически совпадающие с точной формулой (1).

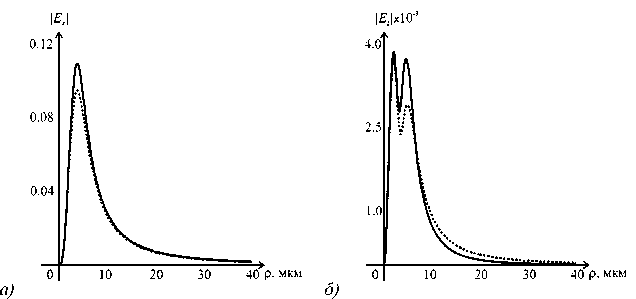
Рис. 2 Дифракция гауссового пучка на СФП при z = 10 мкм: поперечная составляющая E_x (а)

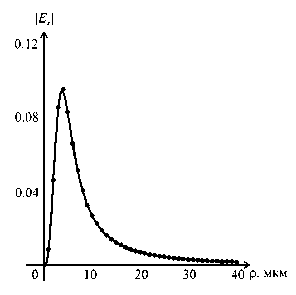
Рис. 3 Сравнение результатов расчета картины дифракции гауссового пучка с использованием приближенной формулы (11) (сплошная кривая) и с помощью точной формулы (1) (график показан отдельными точками)

и продольная составляющая Ez (б) (сплошная кривая – в параксиальном приближении, пунктирная – в непараксиальном)

Заключение

В работе получены аналитические выражения, описывающие параксиальную и непараксиальную векторную дифракцию гауссового пучка на СФП. Численно показано, что при использовании обоих приближений полученная амплитуда может отличаться более, чем на 10%. Также показано, что продольная составляющая в некоторых случаях может составлять несколько процентов от поперечной.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-Sa-06), а также грантов РФФИ 05-0850298 и 07-07-97600.