Непараксиальное моделирование распространения бесселевых пучков

Существует множество подходов к решению задач распространения света. При этом разделяют области дифракции на параксиальные и непараксиальные (расстояния сравнимы с длинной волны [1]).

Известны аналитические соотношения для скалярных как бездифракционных, так и расходящихся бесселевых пучков. Бездиф-ракционный бесселевый пучок может быть непараксиальным и удовлетворять уравнению Гельмгольца, а может быть параксиальным и преобразовываться с помощью параболического преобразования Френеля.

Бесселевые пучки часто используются в качестве оптических ловушек для микрочастиц, когда возможно одновременно захватить и манипулировать цепочкой микрочастиц [24]. При этом чтобы изменить масштаб пучка часто прибегают к использованию такого элемента, как сферическая линза. В работе [5] показано, что при изображении бездифрак-ционного бесселевого пучка он переходит в расходящийся бесселевый пучок.

Однако аналитические решения не позволяют рассчитать картину дифракции реального, ограниченного диафрагмой или искаженного (например, захваченной частицей) пучка. В этом случае одним из эффективных методов расчета распределения светового поля в рамках скалярной теории является использование интегральных операторов распространения. В данной работе рассмотрен общий подход реализации операторов для решения задачи распространения бесселевых пучков. Для этого была разработана программа, включающая в себя оптимизированные алгоритмы решения данных задач для системы CAAM [6], а также реализован для нее удобный интерфейс, позволяющий компоновать различные алгоритмы в любом сочетании и последовательности.

Постановка задачи

Рассмотрим различные области распространения бесселевого пучка:

^>( r , Ф ) = J n ^{( a r )e}xp⁽ inT ), (1) где J_n ( х ) – функция Бесселя первого рода n -го порядка. При численном моделировании будем считать, что бесселевый пучок ограничивался на входе круглой апертурой радиуса R =0,5 мм, длину волны примем условно равной l=1 мкм. Число отсчетов всех получаемых изображений - 256 x 256. Далее во всех примерах будет рассматриваться мода Бассе-ля с параметрами n= 1 или n= 0 , a=40 .

Для сравнения результатов использовалось среднеквадратичное отклонение амплитуды пучков по формуле:

б =

jj (U0( x, y, z )|- U(x, y, z )| )2 d x d y jj U0( x, y, z )|2 d x d y         ,    (2)

где U ₀( x , y , z ) – комплексная амплитуда поля на расстоянии z от входной плоскости для аналитического решения, U ( x , y , z ) – соответствующая комплексная амплитуда поля, полученная численно при помощи операторов распространения.

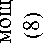
инвер. ампл.

фаза

инвер. ампл.

фаза

инвер. ампл. фаза z = 100 мм, 5 = 98,6 %

z = 3 мм , 5 = 6,73 %

z = 20 мм , 5 = 27,2 %

Рис. 1. Сравнение аналитического решения (7) с результатами непараксиального моделирования распространения ограниченного бесселевого пучка на различных расстояниях z.

Известно [7], что ограниченный диафрагмой бесселевый пучок сохраняет свои модовые свойства до расстояния:

Y ( p,0, z ) _ exp

V

2 zα ²

i

2 k

J_n ( αρ ) exp( inθ )

где

2πR   kR z^^         вх __ вх zmax                     ,

λα α

x 2  + y²

max max

.

Из (2) получаем, что для принятых нами параметров бесселевого пучка z _max= 78 мм.

Кроме того, для определения параксиальной зоны для операторов распространения существует условие:

Аналитические решения (6) и (7) являются математической абстракцией, которую невозможно реализовать на практике в связи с бесконечностью бесселевого пучка. Для исследования свойств ограниченных апертурой бесселевых пучков воспользуемся преобразованием Кирхгофа:

z                e^Ukr ( . 1Y _

¥ ⁽ x , y , ^z ) ^_-— ff^ 0 ^{( 5 ,} n) — I ik ^- U^^n . (8) 2П ^J*           Г V r)

z □ V( x ^- 5 ) 2 + ( У ^- П ) 2 ,           ⁽⁴⁾

и условие возможности использования скалярных непараксиальных операторов:

kr □ 1 .                      (5)

Условия (4) и (5) достаточно “размыты”, но на основании исследований, проведенных в [8], можно считать, что непараксиальная зона соответствует диапазону от 0,01 до 10 мм, а параксиальная начинается от 10 мм.

Непараксиальныйбесселевый пучок

В [5] показано, что непараксиальный бесселевый пучок, удовлетворяющий уравнению Гельмгольца

Y ( r , ф , z ) _ i n Jak exp |^ iz-jk ² - a ² ^ J_n ( ar )exp( in^ ) , (6)

после преобразования Френеля остается непараксиальным бесселевым пучком с точностью до фазового множителя:

На рис. 1 приведены результаты численного моделирования с использованием выражений (7) и (8). Видно, что аналитическая формула для непараксиального пучка дает неизменную картину модовой структуры, приобретающую по мере распространения лишь набег фазы. Моделирование же ограниченного пучка отражает реальную картину разрушения модовой структуры на расстоянии, близком к (3). Из графика зависимости отклонения (2), представленного на рис. 2, видно, что погрешность превышает 15% уже на расстоянии более 10 мм.

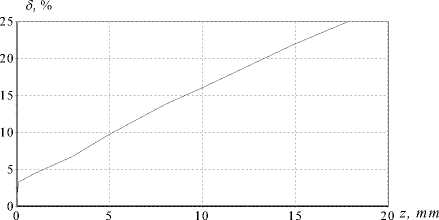
Рис. 2. График зависимости отклонения амплитуды от идеальной моды (2) для непараксиальной зоны

s

С

инвер. ампл. фаза z = 10 мм , R вых = 2 мм

инвер. ампл. фаза инвер. ампл. фаза z = 30 мм, Rвых= 0,67 мм      z = 60 мм, Rвых= 0,33 мм

Рис. 3. Сравнение аналитического решения (9) при r₀ = 0,128 мм с результатами параксиального моделирования распространения ограниченного бесселевого на различных расстояниях z

Параксиальныйбесселевый пучок

В [5] приведено аналитическое решение параксиального уравнения Гельмгольца (типа Шредингера) в виде параксиальной цилиндрической волны:

^ 1 ( r , Ф, z ) = ^{( -} i ) ^{n +}\ rlk - exp ' ^i— ( V 2 n z L 2 z

( r ² + Г -

\АЛ -rr )      x

) J n I —I exp( inv ) ,

(9) где r₀ – произвольный параметр системы.

Из ур. (9) видно, что такой бесселевый пучок дифрагирует (расходится) по мере распространения вдоль оси z в отличие от непараксиального пучка (6) или (7), который неподвержен дифракции и не расходится при распространении.

Обычно пучок (9) формируется с помощью узкой кольцевой диафрагмы в непрозрачном экране [7]. Однако его можно моделировать и с помощью преобразование Френеля:

На рис. 3 приведено сравнение аналитического выражения (9) для выходного радиуса 1 мм с результатами численного моделирования с помощью интегрального оператора (10) для различных значений Rвых, на вход которому был подан ограниченный круглой апертурой бесселевый пучок (1). Параметры а и r0 - были согласованы так, чтобы у пучков были одинаковые масштабы. Однако численные эксперименты показали, что для сопоставления масштабов пучков необходимо так же корректировать выходной размер ограниченного апертурой пучка. На рис. 4а показана зависимость размера выходного пучка от расстояния, на котором рассматривается пучок. Она оказалась обратной, что говорит о прямой зависимости расходимости пучка от пройденного им расстояния. В самом деле, если сравнивать формулы (1) и (9), то можно вывести следующую зависимость k r r f ik                         Й

^ i ( x , У , ^z ) = — exP , ^{[ (} x - ^ ) ^{+ (} У - П ) ] -^ i ~ П ^)d 5 ^d П , 2n,z         2 z

-r-r используя в качестве входной функции (1).

kr а = —-z

.

В выражении (11) параметр а играет

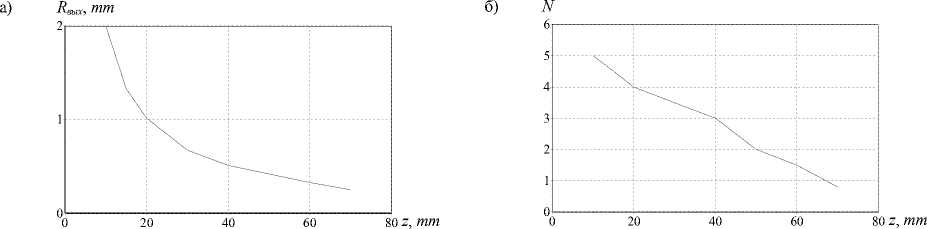
Рис. 4. Графики, полученные с помощью выражения (10) при исследовании распространения параксиального бесселевого пучка в зависимости от:

а – масштаба картины пучка на выходе; б – числа сохранившихся колец от пройденного пучком расстояния z

инвер. ампл. фаза инвер. ампл. фаза z = 10 мм, r0= 0,066 мм z = 30 мм, r0= 0,191 мм

Рис. 5. Демонстрация линейного характера расходимости аналитического решения (9)

инвер. ампл. фаза z = 60 мм , r 0 = 0,382 мм

роль масштабирования, как и в (1) или в (6). Подбирая параметр r₀ можно получить пучки одинакового масштаба, как показано на рис. 3.

При исследовании распространении пучка в параксиальной области до максимального расстояния (3), на котором ограниченный пучок начинает разрушаться, была получена зависимость скорости разрушения от расстояния, пройденного пучком. Она представлена на рис. 4б, которая показывает, сколько колец (по вертикальной оси параметр N ) еще не разрушено. Эта зависимость была получена путем подбора области просмотра пучка, захватывающей определенное количество колец, при которой СКО не превышало значение 7 %.

На рис. 5 показано, что бесконечный параксиальный пучок уширяется линейно, относительно расстояния его распространения. Здесь параметр масштабирования r0 подбирался пропорционально расстоянию z , в результате были получены картины пучка одного и того же масштаба, что подтверждает справедливость формулы (11).

При рассмотрении (рис. 6) распространения ограниченного апертурой пучка (10) на расстояниях больших, чем z_max > 100 мм, было замечено, что его расходимость совершенно идентична расходимости аналитического параксиального бесселевого пучка (9).

Непараксиальный бесселевый пучок, прошедший через линзу

Бесселевые пучки часто используются в качестве оптических ловушек для микрочастиц. Обычно они формируются с помощью аксикона или дифракционного оптического элемента (ДОЭ), а затем уменьшаются до микро-размера с использованием сферической линзы. Оптическая схема для формирования изображения бесселевого пучка, применяемая для манипулирования микрочастицами, показана на рис. 7.

В работе [5] для случая n =0 показано, что при изображении бездифракционного бессе-

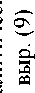
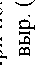
инвер. ампл.

фаза

инвер. ампл.

фаза инвер. ампл. фаза z = 400 мм

z = 100 мм

z = 200 мм

Рис. 6. Сравнение аналитического решения (9 ) при r₀ = 0.49 мм с результатами параксиального моделирования (10) распространения ограничен ного бесселевого пучка на различных расстояниях z.

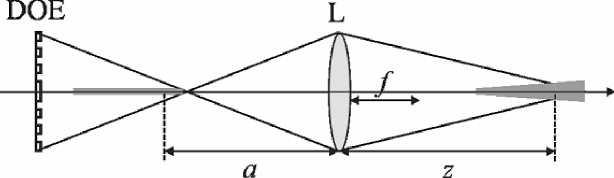
Рис. 7. Схема прохождения пучка через сферическую линзу.

левого пучка он переходит в расходящийся бесселевый пучок:

^ ( p, z ) =

f

( z - f )

т I afp |

Jo|         I exp к f — z )

• a ² 1       fz ) .

— гтт1 a 1 ~----| +1

2 k

f ^{— z}

kp ²

2( f - z ) ’

Из ур. (12) видно, что бесселевый пучок расходится при z >  f . Это связано с тем, что линза вносит в бесселевый пучок расходящийся параболический волновой фронт.

Численно промоделировать действие оптической схемы, представленной на рис. 7, можно следующим образом: выполнить преобразование Френеля (10) для входного пучка (1), произвести умножение на функцию тонкой параксиальной сферической линзы:

^{т (}§, П ) = exp

—

^7 ( f ²⁺ n² ) , ² f          _

и выполнить еще раз преобразование Френеля (10).

Реализовав численную модель, удовлетворяющую выражению (12) как аналитическое решение, а также промоделировав пос-

ледовательное вычисление (10), умножение на (13) и снова (10) как решение пучка ограниченного апертурой, можно получить амплитудно-фазовые картины бесселевого пучка, прошедшего через сферическую линзу на различных расстояниях z , а также СКО, рассчитанные по формуле (2). В результате получим данные для сравнения в виде иллюстраций, показанных на рис. 8 (для постоянного a ) и на рис. 9 (для постоянного f ). Из рисунка также видно, что пучок на любых расстояниях расширяется. Это объясняется свойствами сферической линзы, модель которой представлена на рис. 7. Далее рассмотрим диаграммы СКО аналитического решения. На рис. 10а показано СКО при фиксированном a , на рис. 10б – при фиксированном f . Можно отметить, что чем шире становиться картина пучка тем ниже СКО.

Заключение

В данной работе реализован быстрый алгоритм вычисления интегральных операторов распространения света в свободном пространстве. С использованием данного

инвер. ампл. фаза z = 17,3 мм, 5 = 17,83 %, a = 15 мм, f = 8 мм.

инвер. ампл. фаза z = 30,06 мм, 5 = 6,36 %, a = 15 мм, f = 10 мм.

инвер. ампл. фаза z = 61,65 мм, 5 = 3,13 %, a = 15 мм, f = 12 мм.

Рис. 8. Сравнение аналитического решения (12) с численным моделированием прохождения через линзу (13) на различных расстояниях z при фиксированном расстоянии до линзы a

инвер. ампл. фаза инвер. ампл.

z = 72,05 мм, 5 = 4,31 %, a = 19 мм, f = 15 мм.

фаза

инвер. ампл. фаза z = 37,75 мм, 5 = 11,48 %, a = 25 мм, f = 15 мм.

z = 52,5 мм , 5 = 4,47 % ,

a = 21 мм , f = 15 мм.

Рис. 9. Сравнение аналитического решения (12) с численным моделированием прохождения через линзу (13) на различных расстояниях z при фиксированном фокусном расстоянии линзы f.

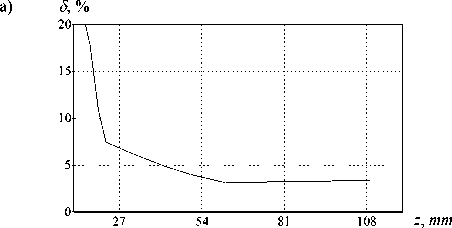
б)

5 , %

27           54           81           108

z , mm

Рис. 10. График зависимости СКО от расстояния, пройденного пучком после линзы для различных параметров: а) a=15 мм; f=7 : 13 мм. б) f=15 мм; a=18 : 25мм

алгоритма было проведено моделирование распространения ограниченных апертурой бесселевых пучков и сравнение модовых свойств этих пучков с известными аналитическими соотношения для скалярных как без-дифракционных, так и расходящихся бесселевых пучков.

Показано, что ограниченный апертурой бесселевый пучок уже на расстоянии в 20 апертур теряет свои бездифракционные свойства и начинает расходиться, при этом степень расходимости полностью соответствует расходимости аналитического параксиального бесселевого пучка. Также показано, что в параксиальной зоне имеется полное соответствие поведения расходящегося бесселе-вого пучка, прошедшего через изображающую линзу, при численном моделировании и использовании аналитического выражения.

Работа выполнена при частичной финансовой поддержке российско-американской про- граммы “Фундаментальные исследования и высшее образование” (грант CRDF RUXO-014-SA-06), а также гранта РФФИ 07-07-97600.