Непараксиальное распространение гауссовых пучков под углом к оси анизотропного кристалла

Всё больший интерес и практическое применение приобретают оптические устройства, позволяющие преобразовывать одни свойства электромагнитного излучения в другие. Среди наиболее востребованных можно назвать поляризационные и модовые преобразования. В частности, теоретически и экспериментально показаны преимущества радиальной и азимутальной поляризации лазерного излучения по сравнению с линейной поляризацией в приложениях, использующих острую фокусировку [1–3]. Однако большинство современных лазеров генерируют излучение с линейной поляризацией, что приводит к необходимости выполнять поляризационные преобразования [4, 5], в том числе с использованием анизотропных кристаллов [6, 7].

Распространение лазерных мод высокого порядка в среде с сильной анизотропией приводит к сложным поляризационно-модовым преобразованиям [8–11], связанным с наличием орбитального углового момента у таких пучков. Причём для анализа таких явлений часто используется параксиальная модель распространения [12, 13].

Заметим, что взаимодействие поляризации и пространственного распределения электромагнитного поля происходит также в изотропной среде в непараксиальном режиме, в частности, при острой фокусировке [14–16].

Непараксиальный режим в анизотропной среде позволяет обнаружить более тонкие эффекты [17 – 20].

В данной работе рассматривается распространение лазерных пучков, в том числе гауссовых, как вдоль, так и под углом к оси анизотропного кристалла. Для одноосного кристалла с использованием метода стационарной фазы получены аналитические выражения, показывающие зависимость астигматического искажения от поляризации падающего пучка. Также показано, что при распространении лазерного пучка под углом к оси кристалла проявляется эффект двулучепреломления, который может исче-

зать при соответствии плоскости наклона пучка и плоскости линейной поляризации. Для гауссовых пучков получено выражение, связывающее параметры пучка и кристалла, при котором обеспечивается визуальное разделение обыкновенного и необыкновенного лучей.

В работах [21, 22] был получен в компактной форме интегральный оператор распространения электромагнитных полей в кристаллах, описываемых следующими тензорами диэлектрической и магнитной проницаемости:

	f e XX	e Xy
g =	^ yx	e yy
	V 0	0
	f Ц XX	M Xy
Ц =	M- yX	M yy
	V 0	0

0 )

^e zz J

0 )

,

.

(1а)

(1б)

M zz J

Векторный интегральный оператор распространения, основанный на разложении по плоским волнам, имеет следующий вид:

( E X ( u , v , z ) )

E ( u , v , z ) = E y ( u , v , z )   =

I E z ( u , v , z ) J f e ox ^(a , ^в) )

Jf   C o W)

a ² + s so ²

e oy ( « , P ) exp [ ik Y o ( « , P ) z ] ⁺ I e« (a , P ) J

[ e ex ( a , P ) )

⁺ c e ( ^a , P ) e ey ( ^a , P ) exP [ ^ik Y e ( ^a , P ) z ]

Iez (a, P)J x exp {ik [au + Pv]} da dp,

> x

где векторы в пространственно-частотной плоскости e _o ( a , P ) и e e ( a , P ) , соответствующие обыкновенному и необыкновенному лучам, распространяю-

поперечных компонент электрического поля ( k =2π/λ – волновое число в вакууме):

щимся в кристалле, определяются значениями рицы следующего вида [21, 22]:

M ( a , P ) =

мат-

M 1 M

M 1 M

(

aP e zz

Ц yx

a ²

^e zz

) Ц yy

P ² ---⁺ ^ xx

V e zz f aP — + e

aP

—+^

X

e

a

zz

- xy

X

Ц zz

V П zz

yx

e

xx

а именно:

e ox ( a , P ) =

e oy ( a , P ) =

1 [,,

= 2 L M 22 -

e ex ( “ , P ) =

e ey ( “ , P ) =

1 [,,

= 2 L M 22 -

e oz ( “ , P ) =

X [ ( ae xx

M 12 ,

M 12 ,

M 11 +V( M 11 e M 22 ) ² + 4 M 12 M 21

M 11 -V( M 11 e M 22 ) ² + 4 M 12 M 21

— +

П zz aP

^e yy

,

П zz

^e xy J

,

,

---------X ^e zz Y o (^a , ^p)

^{+ pe} yx ) e ox ( ^a , ^P ) ⁺ + ( ^ae xy ^+pe yy ) e oy ( ^a , ^P ) ] ,

ee_z ^(a , ^p) = ^-

---------X ^e zz Y e (^a , ^P)

^{X [} ( ^ae xx ^+pe yx ) e ex ( ^a , ^P ) ⁺

⁺ ( ^ae xy ^+pe yy ) e ey ( ^a , ^p ) ] .

Распространение обыкновенного и необыкновенного лучей связано с различными направлениями:

Y o ( ^a , ^p ) =

= ^ [ ( M 22 + M 11 ) + V( M 22 e M 11 ) ² + 4 M 12 M 21

Y e ( a , P ) =

,

j [ ( ^M 22 + ^M 11 )-a/( ^M 22 e ^M 11 ) 2 + ^{4 M} 12 ^M 21

.

Коэффициенты в выражении (2) определяются пространственно-частотным спектром для входных

^f S x ( a , P ) ) = _±X

V S y ( a , P ) J % ²

^Xff ( , y mJ ^exP { “ ik [ “ x ^{+ P} y ] } d x d y ’

^J1 V E y ⁽ x , y ^,0) J

где E_x ( x , y , 0), E_y ( x , y ,0) – поперечные электрические компоненты электромагнитного поля во входной плоскости (при z =0).

Коэффициенты имеют следующий вид:

c o ( “ , ^P ) =

Ce (“, P) =

S x ( ^a , ^P ) e ey ( ^a , ^P ) - S y ( ^a , ^P ) e ex ( ^a , ^P )

^e ox ( ^a , ^P ) ^e ey ( ^a , ^P ) ^e e oy ( ^a , ^P ) ^e ex ( ^a , ^P ) , (7) S y ( ^a , ^P ) e ox ( ^a , ^P ) ^e S x ( ^a , ^P ) e oy ( ^a , ^P ) ^e ox ( ^a , ^P ) e ey ( ^a , ^P ) ^e e oy ( ^a , ^P ) e ex ( ^a , ^P ) .

Выражения (2)–(7) позволяют моделировать распространение произвольных электромагнитных полей в кристалле в непараксиальном режиме с учётом происходящих при этом поляризационных преобразований.

В полярных координатах:

x = r cos ф, a = ° cos ф, u = p cos 6, y = r sin ф, P = ° sin ф, v = p sin 6

выражения (2)–(7) принимают следующий вид:

f E x ⁽ p , ⁶ , ^z ) )

E ( p , 6 , z ) = E y ( p , 6 , z ) =

V E z ( p , 6 , z ) J

= JJ 1 ^C o ⁽° , ^ф) °<° o I

f eox (°, ф) J eoy (°, ф) exP [ikYo (°, ф) z] +

V e oz ( ° , ^ф ) ^J

^f e ex ( ° , ^ф ) )

⁺ c e ( ° , ^ф ) e ey ( ° , ^ф ) exP [ ^ik Y e ( ° , ^ф ) z ]^^X

Veez (°, ф) j

X exp { ik p° cos ( ф e 6 ) } ° d ° d ф ,

где

M ( ° , ф ) =

° ² cos ф sin ф

e

V

^e zz

° ² sin ² ф +^

^e zz

° ² cos ф sin ф

X

Ц zz

°2sin2 ф

V     ^ zz

П yx

xx

^{+ e} yx

e

^e xx

e

° ² cos ² ф

^e zz

° ² cos ф sin ф

^-Ц yy

e

^e zz

° ² cos ² ф

Ц zz

A

X

+ Ц xy J

^+e yy

° ² cos ф sin ф

----^-e xy n- zz              J

,

e oz ( ° , ^ф ) = ^-

о

--------:------ х ^г zz Y о ( ° , ^ф )

^{х [} ( ^г xx cos ^ф+г yx sin ^ф ) e ox ( ° , ^ф ) ⁺ + ( ^г xy cos ^{ф + г} yy sin ^ф ) ^e oy ( ° , ^ф ) ] ,

e ez ( ° , ^ф ) =^-

о

--------х ^г zz Y e (° , ^ф)

^{х [} (^г« cos ^Ф+г yx sin ^ф ) e ex ( ° , ^ф ) ^{+ +} ( ^г xy cos ^{ф + г} yy sin ^ф ) ^e ey ( ° , ^ф ) ^] ,

eox (а, в) = в, eoy (а, в) = -а, eex (а,в) = а, eey (а, в) = в, eoz (а, в) = 0, г0 (а2 +в2 )

e ez ^{( а} , ^в) =--/ ;тг .

г 1 Y 2 ( а , в )

г о -а ² -в ² ,

f ^S x ( ° , ^ф ) ) = X _х

V S y ( о , ф ) ^J % ²

ГГ f E x ⁽ r , Ф ^,0) )      Г z              .

х               expi - ikr о cos ф-ф rr d r d ф .

JJ V E y ( r , ф ,0) J ^{P{           (V V)}}

Y e ( ^а , ^в ) = _А^г о ^- ( ^{а 2 +в} 2 )^ ° .

V                 ^г e

Также упростятся коэффициенты (7):

Если входные поперечные компоненты электриче-

C o ( ^а , 3 ) =

e S x ( а , р ) -а S y ( а , в )

ского поля имеют фазовую вихревую Ex (r, Ф, 0) = E0x (r) exP ( imф) , Ey (r, Ф, 0) = E0y (r) exP ( imФ) , тогда выражение (12) упрощается:

f S x ( ° , ^ф ) ) k m .X

C = T i exP ( im ^ф ) ^х

ISy (°, ф))

зависимость:

C e ( ^а , Р ) =

а ² + в ²

а S x ( а , в ) + в S y ( а , в )

,

а ² + в ²

.

Таким образом, выражение (2) записывается в следующем виде:

E ( и , v , z ) =

J m ( kr о ) r d r .

Л а2 +в2 <о2

в S_x ( а , в ) -а S y ( а , в )

а ² + в ²

f в )

-а

О

V u 7

х

Для многих оптических полей, описываемых через ортогональные полиномы, такие как полиномы Цернике, функции Лагерра–Гаусса, Эрмита–Гаусса, функции Бесселя, выражения (6) и (14) в бесконечных пределах имеют аналитический вид. В конечных пределах также можно получить приближённую аналитическую оценку.

х exp [ ik у _о ( а , в ) z ] +

а S , ( а , в ) + в S y ( а , в )

а ² + в ²

х (19)

х

а

в г о (а2 + в2)

exP ^{[ ik} Y e ( ^а , ^в ) z ^]

Г х

Рассмотрим одноосный кристалл, обладающий только анизотропной диэлектрической проницаемостью (магнитная проницаемость изотропна), ось которого ориентирована вдоль оптической оси. Тогда тензоры (1) примут следующий вид:

V г e Y e ( а , в ) 7

х exp { ik [ а и + в v ] } d а d в .

В изотропной среде, т.е. при г _e = г _о , из выражений (17) следует, что y _e ( а , в ) = Y _о ( а , в ) • Тогда оператор распространения (19) примет следующий вид:

Ё =

f^г •

V 0 f 1

^г о

^Ц= ⁰

V 0

0 )

⁰, ^г e J

0 )

0,

а выражения для векторов (4) и функций пространственного направления (5) значительно упростятся [22]:

Е ( и , v , z ) =

и а2 +в2 <а2

V

л

а

Y о ( а , в )

Y о ( а , в ) J

S ( а , в ) )

^x) ' х (20)

Sy ( ^а , ^в ) ^J

х exp { ik [а и + в v +Y _о ( а , в ) z ] } d а d в ,

что соответствует хорошо известному выражению [23].

Применим к (19) метод стационарной фазы. Используя результаты работы [22], для быстроосцил-лирующих членов в (19) можно записать выражения для соответствующих стационарных точек:

<

<

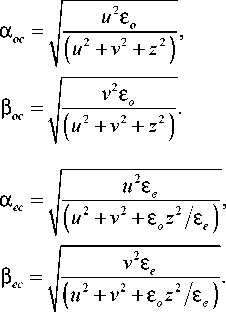
(21а)

(21 б)

Тогда интеграл (19) можно приближённо заменить подынтегральным выражением в стационарных точках:

E ( u . v , z ) =

2л ^в oc⁵x ( ^а oc . ^в oc ) ^-a oc⁵y ( ^a oc . ^в oc )

X

7 H. (^a«. ^в oc )

(в oc

-a G (a ,B ) + oc o \ oc . Voc )

« oc ^{2 +в} oc ²

X

О

V ° 7

+        2 П        ^a ec^x ( ^a ec . ^в ec ) ^{+ в} ec⁵y ( ^a ec . ^в ec )

V H e ( ^a ec . ^в ec )

X

^а, в e

ec

ec

£ o ( ^а ec ^{2 +в}

^a ec ^{2 +в} ec ²

A

G e ( “ ec . в ec ) .

X

‘ ec ² )

--:-----—т e Y (ex ) \ e I e \ ec , V ec )

H o ( ^a oc . ^в oc ) = где

( u ² + V ² + z ² )

7*    '

H e ( « c . ^в c ) =

^£ e ( U ² + V ^{2 + £} o Z ² /^£ e ) ²

^2

.

G o ( ^a oc . ^в oc ) =

= exp { ik J£ V u ² + v ² + z ² } , ^G e ( « ec . ^в ec ) =

= exp

' U ² + V ² +£ o Z ² /£ e } .

^{Так как} ( ^в oc ^a ec ^{- a} oc ^в ec ) = ° . то ^вектор^ы в ⁽²²⁾ ортогональны. следовательно. в общей интенсивности не будет перекрёстных членов.

Выражения интенсивности для поперечных и продольных компонент имеют следующий вид:

I E ox ^{( U} . ^V . ^z )| ^{2 +} | E oy ^{( U} . ^V . ^z )| ² =

=         ( ^{2 n} ) ^{2 z} 2 ^£ o        _X

( u² + v ² )( u ² + v ² + z ² ) ²

^X { V ² I ⁵ x ( ^a oc . ^в oc )|^{2 +} U ² | ⁵ y ( ^a oc . ^в oc )|^{2 -}

^{- UV [ 5} y ^(a oc . ^в oc ) ⁵ x ^(a oc . ^в oc ^{) +}

^{+ 5} x ( ^a oc . ^в oc ) ⁵ * ( ^a oc . ^в oc ) ] } .

| E oz ^{( U} . ^V . ^z )|² = °.

|^Eex ^{( U} . ^V . z f ⁺ | ^E ey ^{( U} . ^V . z ^{) 2} =

=            ( ^{2 n} ) 2 ^z '^£ o £_X

( U ² + V ² )( U ² + V ² +£ o z ² /£ _e ) ² £ e

^X { U ² | ⁵ x ( ^a ec . ^в ec )|^{2 +} V ² |⁵ y ( ^a ec . ^в ec )|²

^{- UV} [ ⁵ y ^(a ec , ^в ec ) ⁵ x ^(a ec . ^в ec ^{) +}

+5X (aec, pec) 5* (aec, p^)!]-, x ec ec y ec ec

,                ,₂              ( 2 п ) ² £ _o

I E ez ^{( u} . ^V . ^z ) =      —TTY

( U ⁺ V ^+£ o z /^£ e )

^ X ^£ e

^X { U ² |⁵ x ( ^a ec . ^в ec )|^{2 +} V ² I ⁵ y ( ^a ec . ^в ec )|^{2 -}

^{- UV [ 5} y ^(a ec . ^в ec ) ⁵ x ^(a ec . ^в ec ^{) +}

+ 5 _X (a_ec. в_ес) 5 * (a_ec. 3^) 1}.

x ec ec y ec ec

Для многих типов поляризации (линейной. эллиптической) справедливо соотношение:

⁵ x ( ^а , ^в ) = P x ⁵ ( ^а , ^в ) .

⁵ y ( ^а , ^в ) P y ⁵ ( ^а , 3 ) .

где | p_x |² +| p_y | = 1. Тогда общая интенсивность:

I 1₂ I                 |2 ( 2 п ) ² z ²е

I E x ^{( u} . ^V . ^z ) ⁺ E y ^{( u} . ^V . ^z ) =-f4---- TT^X ( U + V )

X

+

|P x ^V - P y^U|²

( U ² + v ² + z ² ) ²

| P x ^{U -} P y^V|²

1 ⁵ ( ^a oc . ^в oc )|^{2 +}

( U ² + V ² + £ o z ² |^E z ^{( U} . ^V . ^z ^ =

£ . ) ‘

£>^£ e

1 5 ( а ec . в ec )|² .

2 n)²| p_u - pV    ²

= /, )        7 ,2 £ ° 5 ( a .c . p .c )l .

( u^{1 +} V ^{1 +}£ o z²²e , ) ^£.

Из выражений (27) следует. что картина интенсивности зависит как от пройденного расстояния z . так и от поляризации. Однако в параксиальном слу-

2 22

чае, когда z >> u + v , зависимость от пройденного расстояния будет незначительной, в то время как зависимость от поляризации останется заметной. Причём различие будет тем существенней, чем сильнее отличаются обыкновенная и необыкновен- ная диэлектрические проницаемости.

При линейной поляризации изменение соотношения параметров p x и p y соответствует повороту вокруг оси кристалла на угол т = tan ^{- 1} ( p y I p_x ). Т.к. в этом случае значения p x , p y действительные и неотрицательные, то будет происходить соответствующее астигматическое искажение входного пучка.

При круговой поляризации выражения (27) примут следующий вид:

|Ex ⁽ u , v , z )Г ⁺ | E y ⁽ u , v , z )|² = ( ^{2 n} ) 2 z 2 ^е o ^X

I S (a oc , P oc )|2   ( -o      | S (a ec , в ec )| 2

( u ² + v ² + z ² )     ^- e ( u ² + v ² + - o z ²/- _e )

|^Ez ⁽ u , v , z )| 2 =

(2n)2 (u2 + v2)

( u 2 + v 2 +- oZ 2 /-e )2

S ( a ec , в ec )|² , ^- e

который говорит об отсутствии астигматических искажений.

Вклад в общую интенсивность продольной компоненты с ростом расстояния z будет уменьшаться.

Как правило, при анализе распространения лазерных мод в анизотропных средах исследуются орбитально-спиновые преобразования [8– 11, 14, 15] и астигматические изменения [20, 24]. Причём данные явления наблюдаются либо при фокусировке лазерного излучения, либо при распространении под углом к оси кристалла. В работе [25] было показано, что наличие вихревой фазовой сингулярности в лазерном пучке приводит к визуальному астигматизму при распространении как вдоль, так и перпендикулярно оси кристалла.

Для гауссовых пучков пространственный спектр имеет аналитическое выражение. В частности, для эллиптического пучка Эрмита–Гаусса (ЭГ):

E HG ^{( x} , У ^,0) = ^A nm exp

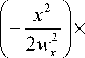
H m

X H n

(

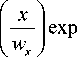
V

2 y^ ² ", J

( A x

w

V y J

,

где H_n ( x ) - полином Эрмита n -го порядка, w_x , w y -радиусы перетяжки гауссова пучка вдоль соответствующих осей, A_nm – нормировочная константа, спектр (6) в бесконечных пределах будет иметь следующий вид:

S HG X H n	( a , p ) = - w s f a 1 |       | exp V "sx J	nm exp x w sy 1 -Л1 2 w 2 V       s, J	a 2 1 2 w 2x j		IX J
			II H n	I - w V sy
где w sx	= ( k" x ) - 1 ,	" sy =( kw, )		1 .

При распространении вдоль оси кристалла даже если изначально пучок был не эллиптичный ( w y = w x ), то при линейной поляризации, учитывая (27), постепенно он будет претерпевать астигматические изменения.

Для пучков Лагерра–Гаусса (ЛГ):

E LG ⁽ r , ф ^,0) =

₂             m ₂

I      r 1l r 1 Tml I r I                     ( )= Anm exp| - II — I Ln1 I I exp (im ф)

V 2w0 JVw0 J     Vw0 J пространственный спектр (14) имеет также радиально-вихревой вид:

S lg ( о, Ф ) =

m

° II - I X

² w JV w J

= Anm (-i)m (-1)n exp I -w           V

XLm f°^1 exp (imф) =

Vw^ J

= ^S L ^m ( ° ) exp ( ^{im ф} ) , где w = ( k" ^ ) ^{- 1} .

В общем случае при наличии в лазерном пучке несущей пространственной частоты:

cr ( x , y , 0) = exp ( ikq_xx + ikq y y )                   (33)

можно считать, что пучок распространяется под углом к оси кристалла:

n /2.2 v= 2 qq,+q,

и спектр в (6) будет смещён пропорционально несущим пространственным частотам:

Sq (a P) =

= tt f f E ^{( x} , y ) exp ( ikq x x ^{+ ik}q , y ) ^X

^Л a                                      (35)

X exp {-ik [ax + Py ]} dx dy =

= S ( a^{- q} _x , P^- q y ) .

Таким образом, в выражениях (27) спектр будет использоваться в смещённых стационарных точках.

Заметим, что при внесении в пучок (31) про- странственной несущей частоты:

cr ( r , ф , 0) =

= exp ( ikr o ₀ cos( ^ - ф ₀ ) ) ,

где о0 = qq+ + q2 , ф0 = tan 1(qy I qx), пространствен- ный спектр уже не будет иметь радиально-вихревой зависимости.

Рассмотрим распространение фундаментальной гауссовой моды под углом (36) к оси кристалла. Тогда спектр в формулах (27) будет иметь следующий вид (положим w _{s y} = w_sx = w_s ):

SG («oc , в oc ) =

A

= -nm exp w s ²

( nou ^- q x R o ) 2 ⁺ ( n o v ^- q y R o ) 2

2 w 2 R o

(37а)

Рис. 1. Мода ЛГ (n, m) = (3, 0) во входной плоскости (при z = 0): распределение интенсивности (а) и фазы (б)

Моделирование распространения под углом к оптической оси выполнялось за счёт умножения исходного распределения на фазовый множитель вида (33). В этом случае фаза входного распределения изменится, как показано на рис. 2.

SG («ec , в ec ) =

A

= -nm exp w s ²

^^^^^^s

( neu - qxRe ) +( nev - qyRe )

2 w s ² R e ²

,

(37б)

V                                7

где     R_o = V u ² + v² + z ² ,     R e = V u ² + v² + n o z ²/ n 2 ,

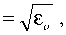
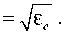
Как видно из (37), обыкновенный и необыкно-

венный лучи будут визуально разделяться только

при достаточно больших значениях пространствен-

ных несущих частот (33):

3 w ( z ) n_on_e ²

qx, y >7/2   2 V

kz ( ne - no )

где

w ⁽ z ) = w 0

4 z ²

⁺ k² w 4

– радиус гауссова пучка на расстоянии z .

• 4.    Моделирование распространения гауссовых пучков под углом к оси кристалла

• 4.1.    Распространение вдоль оси кристалла

• 4.2.    Распространение под углом к оси кристалла

Рассмотрим распространение пучков ЛГ в кристалле рутила [20]: ε 0 =6,84, ε e =8,43. Данный кристалл был выбран для наглядной демонстрации эффектов двойного лучепреломления, т.к. имеет существенное различие в значениях диэлектрической проницаемости.

Параметры моделирования: длина волны λ = 1 мкм, радиус пучка R = 15 мкм, радиус перетяжки W 0 =3 мкм.

В данном разделе приведены результаты моделирования распространения мод ЛГ вдоль оси кристалла при различных поляризациях входного пучка. В качестве входного распределения использовалась мода ЛГ ( n, m ) = (3,0) (см. рис. 1).

Результаты моделирования (см. табл. 1) показывают полное соответствие теоретическим выкладкам, а именно: наличие астигматических искажений при линейной поляризации и их отсутствие при круговой поляризации.

В данном разделе приведены результаты моделирования распространения мод ЛГ под углом к оси кристалла при различных поляризациях входного пучка. Наклон к оси кристалла был выбран вдоль оси x , и пространственная несущая частота определялась с учётом выражения (38): q_x = 0,5 ( у = 45 ^o ).

Рис. 2. Фаза моды ЛГ (n, m) = (3,0) с пространственной несущей во входной плоскости

Как видно из табл. 2 и 3, при наличии во входном пучке обеих поперечных компонент (при различных типах поляризации) наблюдается эффект двойного лучепреломления. Таким образом, если линейно-поляризованный лазерный пучок распространяется под углом к оси кристалла, то вращение кристалла вокруг его оси будет приводить к появлению или исчезновению второго луча.

Заметим, что двулучепреломление возникает за счёт различия в направлениях распространения двух поперечных компонент электрического поля. При этом направление распространения продольной компоненты совпадает с направлением x -компоненты (рис. 3).

При использовании мод ЛГ с менее выраженным центральным пятном (рис. 4) визуального разделения на обыкновенный и необыкновенный лучи не происходит даже при очень больших углах наклона – в результате формируется сложная интерференционная картина, зависящая от поляризации (табл. 4).

В работе получены следующие основные результаты. Для одноосного кристалла с использованием метода стационарной фазы получены аналитические выражения, показывающие зависимость астигматического искажения от поляризации падающего пучка. При линейной поляризации вращение вокруг оси кристалла будет приводить к соответствующему астигматическому искажению входного пучка. При круговой поляризации астигматические искажения отсутствуют.

Таблица 1. Распространение моды ЛГ (n, m) = (3, 0) вдоль оси кристалла при различных поляризациях (картина полной интенсивности в поперечных плоскостях)

	Линейная x -поляризация			Линейная поляризация под углом 45 ° к оси x			Круговая поляризация
Z =5 мкм
Z =200 мкм
Z =450 мкм		•						•
Z =600 мкм

Таблица 2. Распространение моды ЛГ (n, m) = (3, 0) под углом к оси кристалла при различных поляризациях –

Таблица 3. Распространение моды ЛГ (n, m) = (3, 0) под углом к оси кристалла при различных поляризациях – картины интенсивности в поперечной плоскости при Z = 450 мкм

	E 2	E x 2	E y 2	E z 2
Линейная
x -поляризация
Линейная
поляризация под углом 45 ° к оси x
Круговая поляризация				•    1

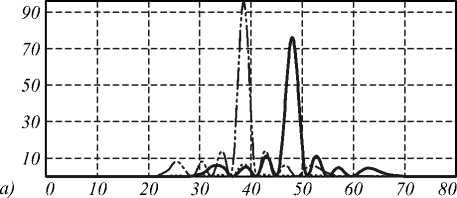
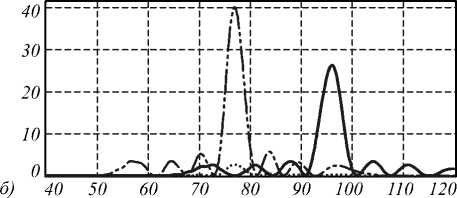
Рис. 3. Соответствие компонент электрического вектора обыкновенному и необыкновенному лучам на расстоянии z = 150 мкм (а) и z = 300 мкм (б) (штрихпунктирная линия – x-компонента, сплошная линия – y-компонента, точечная линия – z-компонента)

• б)

Рис. 4. Мода ЛГ (n, m) = (3, 3) с пространственной несущей во входной плоскости: распределение интенсивности (а) и фазы (б)

Таблица 4. Распространение моды ЛГ (n, m) = (3, 3) под углом к оси кристалла при различных поляризациях –

Также показано, что при распространении лазерного пучка под углом к оси кристалла проявляется эффект двулучепреломления, который может исчезать при соответствии плоскости наклона пучка и плоскости линейной поляризации. Для гауссовых пучков получено выражение, связывающее параметры пучка и кристалла, при котором обеспечивается визуальное разделение обыкновенного и необыкновенного лучей.

Работа выполнена при поддержке грантов РФФИ 10-07-00109-а, 10-07-00438-а, гранта Президента РФ поддержки ведущих научных школ НШ-4128.2012.9.