Непараксиальные гипергеометрические моды

В последнее время возрос интерес к точным решениям параксиального уравнения типа Шредингера в цилиндрической системе координат. Так в [1] рассмотрены гипергеометрические (ГГ) моды. Эти пучки вскоре были обобщены и появились гипергео-метрические-гауссовые (ГГГ) моды [2], ГГ пучки [3] и круговые пучки (КП) [4]. В [4] указано, что частными случаями круговых пучков являются многие известные световые пучки, например, стандартные [5] и элегантные [6] моды Лагерра-Гаусса, квадратичные Бессель-Гауссовые пучки [7], гауссовые оптические вихри [8,9].

Однако уравнение типа Шредингера описывает распространение света в параксиальном приближении, от которого в некоторых случаях приходится отказываться, как, например, в задачах, требующих острой фокусировки лазерного излучения (острая фокусировка может использоваться, например, для уплотнения информации при лазерной записи, в хирургии, для лазерного напыления паров кремния, для сварки в труднодоступных местах).

В данной работе рассматриваются ГГ моды в непараксиальном случае. Получено аналитическое выражение, являющееся точным решением уравнения Гельмгольца в цилиндрических координатах. Это решение пропорционально произведению двух функций Куммера. Далее это решение представлено в виде суммы двух слагаемых, описывающих прямую непараксиальную гипергеометрическую (нГГ+) моду и обратную непараксиальную гипергеометрическую (нГГ-) моду. Эти световые пучки распространяются вдоль оптической оси в прямом и обратном направлениях. Показано, что при больших расстояниях от начальной плоскости (много больших длины волны) нГГ+ мода совпадает с точностью до константы с параксиальной ГГ модой из [1,3].

1. Угловой спектр плоских волн для непараксиальных гипергеометрических мод

Известно, что любое решение уравнения Гельмгольца

(A + k2) E (x, y, z) = 0, где k – волновое число, можно представить углового спектра плоских волн

E (x, У, z ) = п п

= J J f ( 9 , ф ) exp [ - ik ( x sin 9 cos ф+ ,

в

(1) виде

-п 0

+y sin 9 sin ф + z cos 9)] sin 9d9dф где (0, ф) - углы Эйлера, определяющие точку на сфере, задающую направление распространения плоской волны. Рассмотрим конкретный вид углового спектра

х 1 (. 9 У .                     х f (9, ф) = — tan— sin1 (9) exp (2 in ф), x ' 2л( 2J

где n – целое и β – действительное числа. Подставив (3) в (2), получим:

E (r, ф, z) = (-1)n exp (i2nф)х r               I   9 У                      (4)

xJexp(-ikzcos9)1 tan— I J2n (kr sin9)d9, о                 V    2 J где Jv (x) - функция Бесселя. С помощью справочного интеграла [10] вместо (4) можно получить явное аналитическое выражение:

/ , х       ( -1 ) )                      , X

E ( r , ф , z ) = [ (2 n ) !]₂ exp ( i 2 n ф + ikz ) x

хГ

I 2 n — в + 1 -           ।

X 1 F 1 1----2----- ,2 n + 1, x + lx

I 2 n — в + 1 -           ।

X 1 F 1 1----- 2----- ,2 n + 1, x - I ,

где x ±

— 1

■^ik z ±⁽ z ²⁺ r ^{2 ) 12}

(r,φ,z) – цилиндрические

координаты, Г ( x ) - гамма-функция, ₁ F ( a , b , x ) -функция Куммера [10]. Выражение (5) является точ-

ным решением уравнения (1) и описывает сумму двух непараксиальных гипергеометрических пучков:

E ( r , Ф , z ) = E ⁺ ( r , Ф , z ; в ) + E - ( r , Ф , z ; в ), (6) где E⁺ - прямая нГГ⁺ мода, которая описывается выражением (4), в котором интеграл по θ вычисляется от 0 до π/2 , а E^- - обратная нГГ^- мода, которая описывается выражением (4), в котором интеграл по θ вычисляется от π/2 до π . Можно показать, что E - ( r , ф , z ; в ) = E ⁺ ( r , ф , - z ; -p ). Отсюда, в частности,

₁ F₁( a , b , z ) exp ( ± i n a ) z^a Г ( b )    =   Г ( b - a )    ^X

g ( a l n fl^- b l n ( - z )^- n + O d z_r, ) n =0            ⁿ !

exp ( z ) z^a b +------X

^Г( a )

следует, что при z = β = 0 прямая и обратная нГГ моды совпадают и равны выражению:

E ^- ( r , Ф ,0;0) = E ⁺ ( r , Ф ,0;0) = 0,5 E ( r , ф , z ) =      (7)

= ( - 1) n ( n /2)exp( i 2 n ф ) J 2 ( kr /2).

s-1 (b - a) (1 - a)           / s\ g2-----z"n + O(|z| S)

где верхний знак берется для случая

-л/ 2 <  arg z <  3 л/ 2    и нижний

для

Из этого выражения следует, что основная нГГ мода при z = β = n = 0 порождается квадратом функции Бесселя нулевого порядка и имеет диаметр центрального светового пятна 1,53 λ , где λ - длина волны (под диаметром понимается удвоенное расстояние от максимума до первого корня функции Бесселя).

- 3л/2 <  arg z < - л/2. Устремляя R к бесконечности, получим, что

2. Прямые и обратные непараксиальные гипергеометрические моды

В общем случае, когда z * 0 или p * 0, из (5) нужно выделить в явном виде составляющие, описывающие прямые и обратные моды.

Для конфлюэнтных функций известно ассимпто-тическое разложение [11]:

₁ F ( a , b , z )    exp ( ± i n a ) z a

Г ( b )    = Г ( b - a )

f 7 A 1 Y xl a,1 + a -b, — I +

I                z J

exp ( z ) z^{a b + Г}( a )

F

b - a ,1

2 ^F 0 ^X

1 I ^- a ^,— I z J

Подставим (9) в (5) вместо конфлюэнтной функции с аргументом x ₊ :

I X l n 3 jAtY ^{2 n +p + 1} ItI ² n ^- P ^{+ 1} Yfo Xi      V n 77 f ^{2 n -} P ^{+ 1}₀   7     |

E(r,ф,z) = (-1) exp(12nф)Г1----2----|Г1----2----I[(2n)'] (kr) 1F I----2----,2n +1,x-|x x<

г| 2 n + P + 1

I 2

- 2 n -p+1

exp ( ikz ) L+ ikz + ik ( z ² + r ² ) ¹² J    ²

2 n -p + 1

- 2 n -p + 1   1 I

2 , x ₊J +

-2 n -p-1

1-----expГ-iklz- + r’У”If-Ikz-ik(=* + rT] 2 .Ff^F+^I, 2n + p +1 ,±)[ f2n-p +11 pL (     ) JL (     ) J 201 2,2,

I 2 J где 2F0 (a,b, x) - гипергеометрическая функция [10]. Применив преобразование Куммера

1F (a, b, z) = exp (z) 1F (b - a, b, - z),(11)

получим:

n                  i 2n + p +1 । Г2n p +1 ir/,*» \ii—1/7

E ( r , Ф , z ) = ( - 1 ) exp ( i 2 n ф ) г1---- ’---- Jr|---- ’---- I [ ( ’ n ) ^!] ( kr ) x

^x^ ikz L Г _itz + _itU 2 + r 2),. ] '      f 2 n -_g±1 ,-2 n -₽_±1, -| f f 2 n -|p+1 n + _{U l} ) +

rf2n + p +1IL      v ’ J 201   2        2       xJ111   2

I 2 J exp(-ikz) p               !>xtilTT=1 ^f2n + p +1 -2n + p +1 1 | ^f2n + p +1 „ , л |

-ikz-ik z + r            2F,            ,,,F            ,2n +1,-x rf2n-p +1IL        v ’ J 201   2         2     x +J111    2

I 2 J

Обозначив q ± =± ik - + (

-■ - + r 2 )" ,

запишем

выражение для комплексных амплитуд нГГ^± мод: ( — 1 ) n                           .2.

E (r,ф,-) = (2 2 exp(i2nф±ik-)(kr) x

r ( 2n + p +1 W2n-p +1j xr              1

I 2    ) l 2 J

x

хГ

-i

2 n ±P + 1 j    - ( 2 n + P+1)/2

—;— I q ±

Г 2n + P +1 -2n + P +1 -i j

^x 2 F o l — 2—^,—2—^, q ± J ^x

E+ (r,ф,- » 2) - [(2n)!] 1 x

x exp ( i 2 п Ф + ik- + it ) Г l n 2 ^ + ^ J x            (14)

x(2ik-)(e-1)/2 tn 1F1 ^ 2n +в +1,2n +1, -1 j , где t = ikr2/(2-). Выражение (14) с точностью до постоянного множителя совпадает с выражением для комплексной амплитуды параксиальной ГГ моды [1,3] при условии, что m = -1, iY = в , w = k-1 и n заменить на 2n.

^x 1 F 1

Г 2 n + P+ 1

l 2

,2 n + 1, ± x -

Выражение для E ( r , ф , - ) из (12) является суммой E ⁺( r , ф , - ) и E ^-( r , ф , - ) из (13).

Если в выражении (13) для прямой волны E ⁺ ( r , ф , - ) устремить - к бесконечности, то получим

асимптотическое выражение:

3. Моделирование

При распространении вблизи начальной плоскости z = 0 распределение интенсивности для нГГ⁺ пучка изменяется в основном в области боковых лепестков (периферийных световых колец картины дифракции) (рис. 1 а , б ). При z >> λ , когда нГГ⁺ пучок совпадает с ГГ модой, изменения интенсивности происходят только масштабно, а вид дифракционной картины пучка сохраняется (рис. 1 в ).

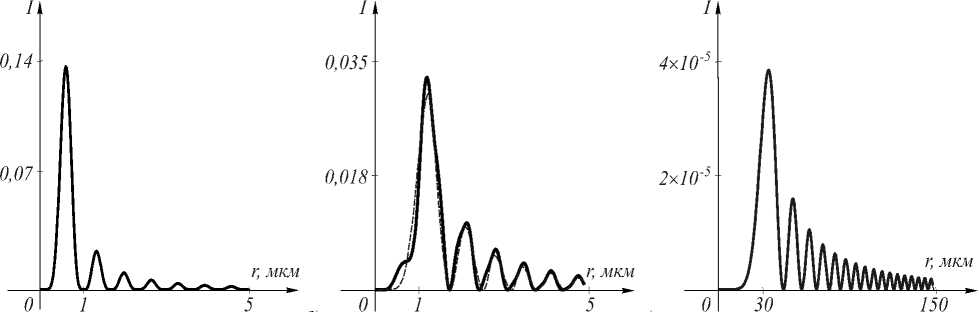
Рис. 1. Распределения интенсивности нГГ+ моды при λ = 633 нм, β = 0, n = 2 на расстояниях z: 0 (а), 1 мкм (б), 1 мм (в)

На рис. 1 показана интенсивность

I=1 Ex Г+IE,11 +1 E-l ’ в относительных единицах при 2=633 нм, в= 0, n=1 при разных расстояниях от z=0, рассчитанная с помощью уравнения (4) при интегрировании от 0 до п/2. На рис. 1 б пунктирная линия - результат расчета по формуле (13).

Для проверки расчетов (рис. 1б) было проведено численное моделирование с использованием программы FullWave 6.0 (производитель RSoft Design, USA, , предназначенной для решения уравнений Масквелла методом FDTD (finite-difference time-domain). В плоскости z=0 было задано электромагнитное линейно поляризованное вдоль оси x поле (7) при n =1, 2=633 нм, с дискретизацией 2/20. На рис. 2а показана картина дифракции такого поля в плоскости z = 1 мкм. Размер картины 5х5 мкм. На рис. 2б показано сечение картины дифракции. Из сравнения рисунков 1б и 2б видно, что они хорошо согласуются между собой, хотя на рис. 1б показана величина Ex 2 , а на рис. 2б I=IE. I’+1E, Г+l E-1'.

Заключение

Итак, в работе получены точные аналитические выражения для непараксиальных гипергеометрических мод, распространяющихся в прямом и обратном направлениях вдоль оптической оси. При больших расстояниях от начальной плоскости прямая непараксиальная гипергеометрическая мода совпадает с точностью до постоянной с параксиальной модой из [1,3].

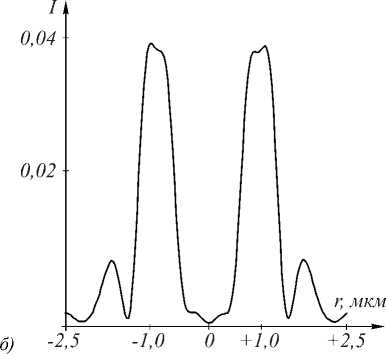
Рис. 2. Картина дифракции I = \ЕД + E y + E_z (а) и ее горизонтальное сечение (плоскостью y=0) (б) для непараксиального гипергеометрического пучка с начальной (z=0) комплексной амплитудой (7) на расстоянии z=1 мкм

Работа поддержана российско-американской программой «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-SA-06), Российским фондом фундаментальных исследований (грант 08-07-99007) и грантом Президента РФ поддержки ведущих научных школ (НШ-3086.2008.9).