Непараксиальные вихревые лазерные пучки Ханкеля первого и второго типов

В оптике известны лазерные пучки, которые описываются скалярными комплексными амплитудами, являющимися точными решениями непараксиального уравнения Гельмгольца. Это хорошо известные плоские и сферические волны [1], моды Бесселя [2], пучки Матье [3], параболические лазерные пучки [4], а также полученные недавно пучки Ханкеля–Бесселя [5] и асимметричные моды Бесселя [6].

В [7] получены выражения для проекций векторов напряжённости электрического (Е-вектор) и магнитного (Н-вектор) полей электромагнитной волны. Все проекции E- и Н-векторов выражены через три интеграла, которые представляют собой разложения по угловому спектру плоских волн. На основе проекций электромагнитного поля получены выражения для вектора Пойнтинга и плотности орбитального момента (ОМ). Заметим, что замкнутые аналитические выражения для ОМ до сих пор получены только для параксиальных пучков Лагерра–Гаусса [8] и для векторных пучков Бесселя [9].

В этой работе рассмотрены новые непараксиальные вихревые пучки, комплексная амплитуда которых описывается функцией Ханкеля полуцелого порядка, поэтому эти пучки названы пучками Ханкеля. Пучок Хан-келя низшего порядка (нулевого) совпадает со сферической волной. Рассмотрены 3 типа таких пучков, которые получаются друг из друга с помощью взятия производных. Рассмотренные лазерные пучки можно сформировать с помощью жидкокристаллического микродисплея и применять для оптического захвата и вращения диэлектрических микрообъектов.

Скалярные непараксиальные сильно расходящиеся пучки Ханкеля

Известно, что комплексная амплитуда непараксиального стационарного светового поля E ( x , y , z ) , удовлетворяющего уравнению Гельмгольца, может быть представлена в виде углового спектра плоских волн

E (x, y, z ) = U A (^, n)x

^{ℝ 2}                                             (1)

x exp ^ ik (^x + ny) + ikz J1 -%2 —П2 ] d^ dn, где k – волновое число монохроматического света, A(ξ, η) – комплексная амплитуда углового спектра плоских волн. В полярных координатах (r, φ) выражение (1) примет вид:

E (r, ф, z ) = jj A (p, 6)x

^{ℝ 2}                                             (2)

x exp ^ ikrp cos (6 - ф) + ikz^ 1 -p2 ] p dp d6, где (ρ, θ) – полярные координаты в Фурье-плоскости. Если амплитуду спектра плоских волн выбрать в виде

A ( p , 6 ) = ^p    exp ( in 6 ) ,

V p2 -1

то вместо (2) можно записать:

E 1, n ( r , ф , z ) = 2 n i n exp ( in ф ) x

xj Jp^ exp (-kz^p2 -1) J (krp) dp,

где J_n ( x ) – функция Бесселя n -го порядка первого рода. Интеграл в (4) является справочным интегралом [10], и вместо (4) можно записать:

^E 1, n ⁽ r , ^ф , z ) = i n ^- 1ⁿ^ r 2nn + 1)/4

(r + z )

x H^ 1I₂ ( k V r ² + z ² ) exp ( in ф )

где H*2) (x) = Jv (x) - iYv (x) - функция Ханкеля, Yv(x) – функция Неймана. Пучки (5) назовём пучками Ханкеля 1-го типа (Х1-пучки). Пучок Ханкеля (5) представляет собой линейный оптический вихрь (x + iy)n, внедрённый в обобщённую сферическую волну Vn+1/2 (R) = Н^ш (kR)R-n-1/2, где R = (r2+ z2)1/2. Функция v(R) зависит только от расстояния до центра системы координат R, поэтому её можно назвать обобщённой сферической волной. Амплитуда (5) имеет особую точку при r = z =0, в которой она равна бесконечности. Можно показать, что амплитуда Х1-пучка при n =0,1 связана с амплитудой сферической волны. Фундаментальный Х1-пучок (при n =0) совпадает со сферической волной, исходящей из начала координат:

E 1,0

- i nV%

р ^{— ikR}           I----------

= 2п----, R = V r ² + z ² . (6)

kR

H 1⁽/²2⁾ ( kR ) R 1/2

При n = 1 получим производную сферической волны с «внедрённым» на оси линейным оптическим вихрем:

E 1,1

= rcV% ( re ^ф )

H 3⁽/²2⁾ ( kR ) R 3/2

„ ( re^{1 ф} ) d ( e ^{— ikR}

= — 2п -- — --

( kR J dR ( kR

Пучки Ханкеля 2-го типа можно получить, дифференцируя комплексную амплитуду (5) по координате z (и умножая на k ^–1 для сохранения размерности):

E2, n (r- Ф, z) = 2n ink—1 exp (in ф)х x2 [г Pn+1

^d z [ j V p ² — i

exp (^— kz^ p ^{2 — 1} ) J n ( kr p ) d p > =

= — 2 n i n exp ( in ф ) x

x j p ^{n + 1} exp ( — kz TpM ) J_n ( kr p ) d p .

Интеграл в (8) тоже справочный [10], хотя можно напрямую дифференцировать правую часть равенства в (5) и воспользоваться рекуррентными соотношениями для цилиндрических функций. Вместо (8) получим:

E 2, n ( r , ф , z ) = i n nyXx

n x            n +32 Hn+3/2 ( k^r 2 + z 2 ) exp ( in ф).      ( )

(₂ r - z ) ^{v 1}

Пучки (9) назовём пучками Ханкеля 2-го типа (Х2-пучки). Эти пучки так же, как и Х1-пучки, по структуре являются обобщёнными сферическими волнами с внедрёнными линейными оптическими вихрями. Отличие только в том, что функция v(R) имеет несколько другой вид Vn+3/2 (R ) = НП+з/2 (kR) R—n—3/2, и в начальной плоско- сти (z =0) амплитуда (9) отлична от нуля только в на- чале координат.

Используя известную приближённую формулу для больших значений аргументов функций Ханкеля

H V²⁾ ( x К Р- i ^V+V2 V п х

exp ( — ix ) , x » 1

можно получить асимптотические зависимости для Х1- и Х2-пучков:

E 1

E 1

∼

∼

r ¹ , r » z ,

,r≪z, n+1 ,              ,

| E ₂| ~ r ² , r » z ,

I E 21 ~ ^ П + т - ^r « ^z . z

Из (12) видно, что интенсивность обоих типов пучков при фиксированном z и с ростом r растёт как rⁿ вблизи оптической оси (это характерное поведение для вихревого пучка), но при больших r интенсивность Х2-пучков спадает быстрее (пропорционально r ^-4), чем интенсивность Х1-пучков (спадает как для сферической волны пропорционально r ^-2). Это означает, что у разных типов пучков Ханкеля разная расходимость. Расходимость обоих типов пучков Ханкеля можно оценить при больших z . Она линейно зависит от z . Действительно, интенсивность Х1-пучков (5) равна:

1 1 ( r , z ) = 2 П ³ -( kr U [ J n + 12 ( ^kD ) + Y n +/2 ( ^kD ) ] ” ( ^kD )

= 2 n ³

( kr ) 2 n     1

( kD ) ^{2 n + 1} п kD

% ² r ^{2 n} D

- 2 n - 2

где D = V r ² + z ² . В (13) при получении приближённого равенства воспользовались известной асимптотикой функций Бесселя и Неймана. Дифференцируя (13) по радиальной переменной r и приравнивая нулю, получим:

d I

— = 0 ^ r = z dr n.

Из (14) видно, что радиус максимума интенсивности вихревых Х1-пучков ( n >0) линейно зависит от продольной координаты z и пропорционален корню квадратному из топологического заряда оптического вихря. Поступая аналогично для Х2-пучков, найдём интенсивность при больших z :

1 ₂ ( r , z ) = 2 п ³ ( kz ) 2 ( kr ) 2 n ( kD ) ^{— 2} n ^{— 3} x

x[ J n + y2 ( kD ) + Y ²+ y2 ( kD ) ] ”

= 2 п ³

( kz ) 2 ( kr ) 2 n 2

( kD ) ^{2 n + 3} n kD

= % ² z ² r ^{2 n} D -^{2 n — 4}

и приравняв к нулю её производную, получим:

d I₂              n

—2 = 0 ^ r = . -z .

d r           V 2

Из сравнения (14) и (16) видно, что расходимость Х2-пучков в 2 раз меньше, чем расходимость Х1-пучков. Примерно можно сказать, что Х1-пучки при n = 1 расходятся в угле 45 градусов, а Х2-пучки – в угле 32 градуса. С ростом номера n углы расходимости увеличиваются.

При любом z точно найти зависимость радиуса максимальной интенсивности можно для Х1-пучка с n = 1. В этом случае интенсивность имеет вид

1 1 ( r , z ) = n ² X r ² D ^; [ J 322 ( kD ) + Y 322 ( kD ) ] =

= ( 2 n ) 2 k ² r ²

1            1

" kD^ + ( kD ) ⁴

Приравнивая к нулю производную интенсивности (17) по переменной r , получим:

= 0 ^ r = k -¹ ^I + ( kz ) ² + ( kz ) ⁴ - 1.         (18)

d r

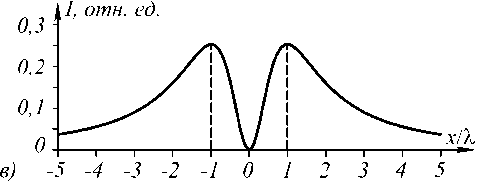
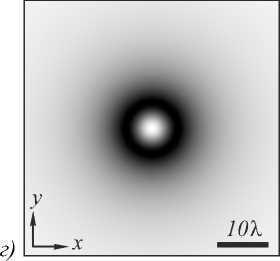
На рис. 1 показаны интенсивность ( а , г ), фаза ( б , д ) и радиальное сечение интенсивности ( в , е ) для Х1-пучка с топологическим зарядом n = 1 на расстояниях z = X ( а, б, в ) и z =5 X ( г, д, е). По горизонтальной оси на рис. 1 отложена радиальная координата в длинах волн.

тенсивности равен r = 0,994λ. То есть не только в дальней зоне (14), но и в ближней зоне расходимость Х1-пучка ( n = 1) равна 45 градусам.

Заметим, что у обоих типов пучков нет боковых лепестков. Известны статьи [11–13], в которых специальными методами уменьшают контраст боковых лепестков лазерных оптических вихрей, чтобы эффективно использовать их для оптического захвата микрообъектов. В данном случае в этом нет необходимости, так как пучки Ханкеля распространяются без боковых лепестков.

На рис. 2 показаны интенсивность ( а , г ), фаза ( б , д ) и радиальное сечение интенсивности ( в , е ) для Х1-пучка ( а , б , в ) и Х2-пучка ( г , д , е ) с топологическими зарядами n = 5 на расстоянии z = 5 X . Из рис. 2 в и 2 е можно видеть, что расходимость у Х1-пучка больше, чем у Х2-пучка при одинаковых топологических зарядах. Радиус максимальной интенсивности на рис. 2 в равен 11 λ , а на рис. 2 е – 7,9 λ .

б)

б)

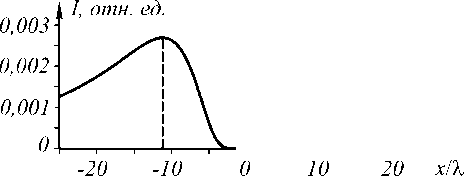
1, отн. ед.

0,012-

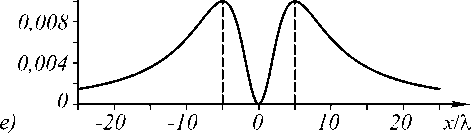
Рис. 1. Интенсивность (негатив) (а, г), фаза (б, д) и радиальное сечение интенсивности (в, е) для Х1-пучка с топологическим зарядом n = 1 на расстояниях z = А (а, б, в) и z = 5А (г, д, е)

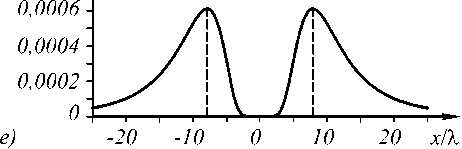
Рис. 2. Интенсивность (а, г), фаза (б, д) и радиальное сечение интенсивности (в, е) для Х1-пучка (а, б, в) и Х2-пучка (г, д, е) с топологическими зарядами n = 5 на расстоянии z = 5А

Вертикальными линиями на рис. 1 в и рис. 1 е показаны максимумы интенсивности в сечении, радиусы которых можно точно найти по формуле (18). Например, для сечения на рис. 1 в радиус максимальной ин-

Аналогично, как из амплитуды Х1-пучка (5), с помощью дифференцирования (8) был получен Х2-пучок (9), так же из Х2-пучка дифференцированием по z можно получить пучки Ханкеля 3-го типа (Х3-пучки):

E 3, _n ( r, ф , z ) = i n 1 nVX k ¹ r n exp ( in ф ) х

x

^k z¹ H^n+5/2 ( k^r^Tz ) ^Н П ²+ 3/2 ( W r 2 ⁺ z ² )

_

/ 2       2 1^{(2 n +5)}/⁴

⁽ r ⁺ z )

/2     2 1^{(2 n +3)}/⁴

⁽ r ⁺ z )

Заметим, что у всех пучков Ханкеля (5), (9) и (19) один и тот же топологический заряд n , хотя радиальная структура пучков описывается функциями Хан-келя разных порядков. Это означает, что хотя нормированный на единицу мощности (или на один фотон) орбитальный угловой момент (ОУМ) этих пучков одинаковый (он равен топологическому заряду), но ненормированный ОУМ будет больше у пучка Хан-келя с большей плотностью мощности. Например, из сравнения рис. 2 в и 2 е видно, что максимальная интенсивность для Х2-пучка в два с лишним раза больше, чем максимальная интенсивность Х1-пучка. Поэтому плотность ОУМ на светлом кольце Х2-пучка будет во столько же раз больше, чем плотность ОУМ на светлом кольце Х1-пучка.

Процесс взятия производных по z от амплитуды пучков Ханкеля можно продолжить, получая пучки Ханкеля более высоких типов. Но для дальнейшего достаточно было получить только три комплексных амплитуды (5), (9) и (19), через которые выражаются компоненты электромагнитного поля векторного пучка Ханкеля [7].

Заключение

Получены в явном виде комплексные амплитуды непараксиальных скалярных сильно расходящихся вихревых лазерных пучков Ханкеля 1-го (5), 2-го (9) и 3-го (19) типов. Все три типа пучков имеют одинаковый целый топологический заряд, но разную зависимость амплитуды от радиальной координаты. Все три типа пучков Хан-келя получаются друг из друга дифференцированием их амплитуды по продольной координате. Интенсивность всех трёх типов пучков Ханкеля имеет радиальную симметрию (в виде «пончика») и не имеет боковых лепестков. Расходимость пучка Ханкеля второго типа меньше расходимости пучка первого типа. Эти пучки не являются модами свободного пространства, так как при распространении меняется распределение интенсивности в сечении пучка, но структура интенсивности (кольцевой вид интенсивности без боковых лепестков) сохраняется.

Работа выполнена при поддержке Министерства образования и науки РФ, гранта Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9), а также грантов РФФИ 13-07-97008, 14-29-07133, 1407-31092, 15-07-01174, 15-37-20723 и 15-47-02492.