Непараметрическая методика проверки гипотезы о независимости случайных величин и ее применение при анализе данных дистанционного зондирования

Универсальным и общепризнанным критерием проверки гипотез о распределениях случайных величин, включая их независимость, является критерий Пирсона [1]. При его использовании необходимо решать задачи разбиения области значений случайных величин на многомерные интервалы и устанавливать закон распределения критерия, определяющего зависимости между вероятностными характеристиками случайных величин. В работах [2–4] предложен новый подход, позволяющий упростить проверку гипотезы о независимости случайных величин с применением непараметрического алгоритма распознавания образов ядерного типа, соответствующего критерию максимального правдоподобия. Идея подхода состоит в решении двухальтернативной задачи распознавания образов. Рассматриваемые классы определяются предположениями о зависимости и независимости случайных величин. На этой основе формируется обучающая выборка по исходным статистическим данным о наблюдениях случайных величин и решается задача распознавания образов. Соотношение между оценками вероятностей ошибок распознавания введённых классов подтверждает либо опровергает рассматриваемую гипотезу.

Цель данной работы состоит в обобщении и развитии непараметрического метода проверки гипотезы о независимости случайных величин для условий большого объёма статистических данных и его применении при анализе информации о дистанционном зондировании антропогенных территорий.

Методика проверки гипотезы о независимости случайных величин

Пусть имеется выборка V = ( x i , i = 1, n ) объёма n, составленная из независимых наблюдений двухмерной случайной величины x = ( x 1 , x 2 ) . Предположим, что выборка V извлекается из генеральных совокупностей, характеризующихся плотностями вероятностей p ( x 1 ) p ( x 2 ) или p ( x 1 , x 2 ) . Необходимо по статистическим данным V проверить гипотезу

H 0 : Р ( ^x 1 , x 2 )^Е Р ( ^x 1 ) P ( x 2 )

о независимости случайных величин x ₁ , x ₂ .

Для проверки гипотезы H0 будем решать двухальтернативную задачу распознавания образов. Под классами Q1, Q2 понимаются области определения плотностей вероятностей р (x1) р (x2), р (x1, x2). В этих условиях байесовское решающее правило, соответствующее критерию максимального правдоподобия, имеет вид m (x):

x gQ i , если p ( x i , x 2 ) <  p ( x i ) p ( x 2 ) , x g Q ₂, если p ( x 1 , x ₂ ) >  p ( x 1 ) p ( x ₂ ) .

В отличие от традиционной постановки задачи распознавания образов при синтезе решающего правила m ( x ) априори отсутствует обучающая выборка, содержащая сведения о принадлежности элементов выборки V к тому или иному классу. Эти сведения должны обнаруживаться в процессе реализации методики проверки гипотезы H ₀ , которая основана на выполнении следующих действий.

По выборке V восстановить плотности вероятностей p (x1, x2), p (x1) p (x2), используя их непараметрические оценки типа Розенблатта – Парзена [5; 6], p (x1, x 2 ) =

n c ₁ c ₂

n

z*

i = 1

i x1   x1

V   c1    7

Ф

x 2

x ₂ ⁱ

c ₂

J

p ( ^x 1 ) p ( x 2 ) =

nn         i          j

_ЕЕф xx ф n c1 c 2 i=1 j=1 V c1 7 V c 2 7

В статистиках p ( x ₁, x ₂ ) , p ( x ₁ ) p ( x ₂ ) ядерные функции Ф ( u v ) удовлетворяют условиям положительности, симметричности и нормированности.

Значения коэффициентов размытости cv , v = 1, 2 ядерных функций убывают с ростом объёма n выборки статистических данных V . Тогда непараметрическое решающее правило классификации случайных величин x = (x1, x 2) запишется как m (x): -

x e Q1, если p (x1, x2) < p (x1) p (x2), x g Q2 , если p (x1, x2) > p (x1) p (x2).

Оптимальные коэффициенты размытости ядерных функций решающего правила m (x) выбираются на основе анализа аппроксимационных свойств непараметрических оценок плотно- стей вероятностей p (x1, x2), p (x1), p (x2) из условия минимума, соответствующих им оценок среднеквадратических отклонений от p (x1, x2), p (x1), p (x2). Например, для p (x1) подобным критерием является [7–11]

®                   n

I ^{p 2} ( ^x 1 ) ^dx1 ^--J p ( ^{x j} ) .

• -M                 j =

Определим оценки вероятностей ошибок распознавания образов р 1 ( С ( 1 ) ) , p ₂ ( С ( 2 ) ) решающим правилом m ( x ) по исходным статистическим данным V при оптимальных коэффициентах размытости С ( 1 ) = ( С 1 ( 1 ) , С 2 ( 1 ) ) , С ( 2 ) = ( С 1 ( 2 ) , С 2 ( 2 ) ) ядерных функций статистик p ( x 1 ) p ( x ₂ ) , p ( x 1 , x ₂ ) соответственно.

Значения p t ( С ( 1 ) , С ( 2 ) ) вычисляются в режиме «скользящего экзамена» по выборке V в предположении, что её элементы принадлежат классу Q t ,

n

P t ( С ( 1 ) , с ( 2 ) ) = - £ 1 ( 5 ( j ) , 5 ( j ) ) , t = 1,2, n j = 1

где S ( j ) = t - указания типа x t = ( x t , x t ) gQ t ;

ц j ) =

t , если x j g Q _t

0, если x^j £ Q _t

• - «решение» алгоритма m ( x ) о принадлежности ситуации x j к одному из классов Q _t , t = 1,2.

При вычислении p t ( С ( 1 ) , С ( 2 ) ) в соответствии с методикой «скользящего экзамена» ситуация x j = ( x j , x 2' ) из выборки V , которая подаётся на контроль в алгоритм m ( x ) , исключается из процесса формирования статистик p ( x 1 , x ₂ ) , p ( x 1 ) p ( x ₂ ) .

Индикаторная функция определяется выражением цад,ад)Л0-если s(jK^j)•

^{( U)}, ^(J)) ^если 5 ( j >8( j ) .

Обозначим через p t значение оценки вероятности ошибки распознавания образов в предположении, что элементы выборки V принадлежат классу Q _t , t = 1,2. Сравним значения p 1 , p ₂ .

Тогда гипотеза H ₀ справедлива, если p 1 <  p ₂ . В противном случае при p ₂<  p 1 случайные величины x ₁ и x ₂ являются зависимыми.

При ограниченном объёме n выборки V возникает задача доверительного оценивания вероятностей ошибок распознавания образов. Для её решения используется традиционная методика доверительного оценивания вероятностей либо критерий Колмогорова – Смирнова.

Например, при использовании критерия Колмогорова - Смирнова отклонение D 12 =|p 1 -p ₂| сравнивается с пороговым значением [12]

D ^₽ =\ ln 02) / n .

Здесь р - вероятность (риск) отвергнуть гипотезу H 0 : р 1 = р ₂ . Если выполняется соотношение D 12 <  D p, , то гипотеза H 0 справедлива и риск её отвергнуть не превышает значения р . При D ₁₂ >  D p гипотеза H 0 отвергается.

Формирование наборов независимых случайных величин

Имеется выборка наблюдений V = ( x v , v = 1, k , i = 1, n ) объёма n , составленная из статистически независимых наблюдений компонент многомерной случайной величины x = ( x_v , v = 1, k ) . Вид плотности вероятности p ( x ) априори неизвестен. Необходимо по статистическим данным V , используя предложенный выше критерий проверки гипотез [13–16]

^Hvj ^: Р ( x v , x j ) = Р ( x v ) P ( x j )

для компонент xv , v = 1, k , Xj, j = 1, k, v > j, сформировать наборы независимых случайных величин x (t ) = (xv, v e It), t = 1, m. Количество m наборов компонент случайной величины x неизвестно, а It - множество номеров компонент, составляющих набор x (t).

Предлагаемая методика основана на выполнении следующих действий:

• 1.    В соответствии с приведёнными выше рекомендациями проверить гипотезы H_{v j} для ка-

• ждой пары компонент (xv, xj) многомерной случайной величины x = (xv, v = 1, k). Количество

• 2.    По результатам этапа 1 построить информационный граф G ( X , A ) , где X - множество его вершин, соответствующих компонентам случайной величины x , а A – множество ребер. Между двумя вершинами x_v , x_j имеется ребро, если выполняется гипотеза H_{v j} , т. е. компо-

• ненты xv , xj являются независимыми.

• 3.    Провести анализ информационного графа G ( X , A ) и определить его полные подграфы G ( X_t , A t ) , t = 1, m . Каждая пара вершин подграфа G ( X_t , A t ) имеет ребро, если компоненты случайной величины x являются независимыми. Обнаружить полные подграфы с использованием алгоритмов разрезания исходного графа, которые основаны на анализе его матрицы смежности. Компоненты x _v , v e I t , соответствующие вершинам полного подграфа G ( X_t , At ) , образуют набор независимых случайных величин.

таких пар соответствует значению k ( k - 1)/2 .

Модификация методики проверки гипотезы о независимости случайных величин в условиях больших объёмов статистических данных

При больших объёмах n статистических данных V = (x[, x2 , i = 1, n) в предложенной методике используются регрессионные оценки плотностей вероятностей p (x1, x2), p (x1), p (x2). Эти оценки основаны на сжатии исходной информации, например, V =(x[, i = 1, n) в массив данных V =(p1', zJ, j = 1, N) путём декомпозиции области значений x1 на N интервалов. Здесь zj - центры интервалов дискретизации значений x1, а p1j = P1j /А - оценка плотности вероятности в j -м интервале; А - длина интервала дискретизации; рj - частота встречаемости значений x1i из выборки V1 в интервале под номером j . Тогда регрессионная оценка плотности вероятности p(x1) по данным V имеет вид [17; 18]

1N p (xi )= £ Pi jф ci j=1

<„ j i A . x^ ,

Предлагаемый подход позволяет на порядки сократить объём n исходной статистической информации при оценивании плотностей вероятностей. Особенность статистики типа p ( x ₁ ) позволяет значительно упростить выбор коэффициентов размытости с ядерных функций в статистике p ( x ₁ ) из условия минимума критерия

-¹ £ ⁽ p i - p ⁽ x i ) ) • l = 1

По аналогии осуществляется оценивание плотностей вероятностей p ( x 2 ) , p ( x ₁, x 2 ) . Регрессионные оценки плотностей вероятностей используются при проверке гипотезы о независимости случайных величин в соответствии с предложенной методикой.

Анализ результатов вычислительного эксперимента

Проведено сравнение эффективности предлагаемой методики проверки гипотезы о независимости двухмерных случайных величин и критерия Пирсона в условиях неоднозначных зависимостей при различных объёмах статистических данных [19–21]. Датчики случайных величин x ₁ , x ₂ формировались на основе равномерного закона распределения x ₁ , который использовался при вычислении значений x ₂ в виде нелинейных преобразований x ₁ . При этом на значения x ₂ накладывались помехи с нормальным законом распределения, который имеет нулевое математическое ожидание и среднеквадратическое отклонение ст . Пример значений случайных величин x ₁ и x ₂ приведён на рис. 1.

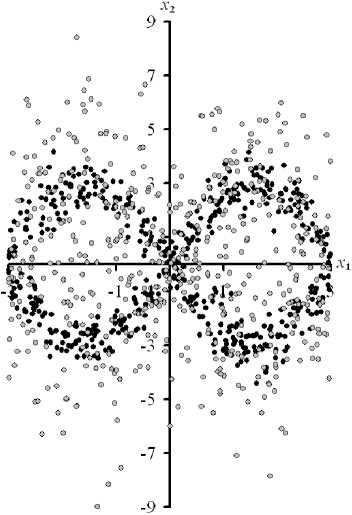
а

Рис. 1. Значения случайных величин x ₁ , x ₂ из выборки исходных статистических данных V при n = 500 и ст = 0,5 (темные точки), а при ст = 2 (серые точки) при использовании зависимостей различной сложности

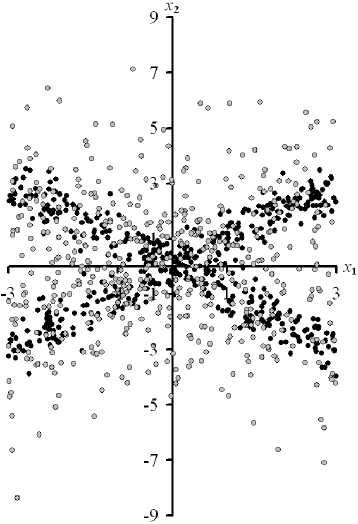
б

Fig. 1. Values x ₁ , x ₂ of random variables from a sample of initial statistical data V at n = 500 and ст = 0.5 (dark dots), and at ст = 2 (gray dots) when using dependencies of varying complexity

При проверке гипотезы о независимости компонент двухмерной случайной величины на основе критерия Пирсона используются результаты оптимального выбора количества интервалов дискретизации [22–24]

__*N =

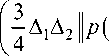
x ₁, x ₂

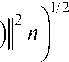
Значение || p ( x 1 , x 2 )||2

да да

= J J P 2 ( x 1 , x 2 ) dx 1 dx 2 , a ^ v — Длина интервала значений случайной

-да -да величины xv , v = 1, 2. Традиционным формулам дискретизации области значений случайных величин посвящены работы [25–27].

По результатам вычислительного эксперимента предлагаемая методика и критерий Пирсона при анализе неоднозначных зависимостей между случайными величинами в условиях относительно малых объёмов статистических данных и средних квадратических отклонений а помех сопоставимы и безошибочно определяют зависимость случайных величин. Данный вывод не соблюдается при зависимости между случайными величинами (рис. 1, а ), когда критерий Пирсона не устанавливает зависимость в условиях n = 100 и а е [0.5; 2]. С увеличением а эффективность сравниваемых критериев снижается. Этот факт объясняется особенностями неоднозначных зависимостей и большими значениями а , когда область определения случайных величин скрывает искомую зависимость. С увеличением объёма n исходных данных эффективность сравниваемых критериев проверки гипотезы о независимости случайных величин повышается. Этот вывод является ожидаемым, так как с ростом n повышаются асимптотические свойства непараметрических оценок плотностей вероятностей и частот встречаемости случайных величин в их двухмерных интервалах. Преимущество предлагаемой методики проверки гипотезы о независимости случайных величин наблюдается при малых значениях а , ограниченных и больших n . При больших n и а часто обнаруживается преимущество критерия Пирсона, если используется процедура оптимальной дискретизации области значений двухмерной случайной величины [22].

Применение предлагаемой методики при анализе данных дистанционного зондирования

Разработанная методика апробирована при анализе данных дистанционного зондирования [2; 28]. Объектом исследования являются антропогенные территории (карьер, пригородная застройка) в окрестности города Красноярска. Исходная информация формировалась по фрагментам съёмки спутника Sentinel-2 на 26.08.2021 (рис. 2). Использовались спектральные каналы xjj , j = 1,9, которые характеризуются длинами волн (нанометры): x 1 - (458-523), x ₂ - (543578), x ₃ – (650–680), x ₄ – (698–713), x ₅ – (733–748), x ₆ – (773–793), x ₇ – (785–899), x ₈ – (1565–1655), x ₉ – (2100–2280).

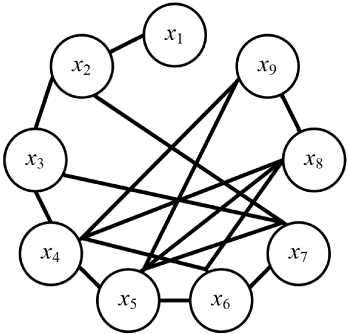
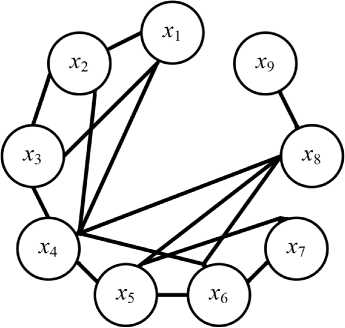
Предлагаемая методика позволяет формировать пары независимых и зависимых случайных величин, изменяя соотношение между их параметрами. Применение методики позволило обнаружить 31 и 29 пар спектральных признаков с сильной линейной зависимостью соответственно для объектов «карьер», «пригородная застройка». Полученные результаты представлены на рис. 3.

Дополнительно обнаружены нелинейные зависимости между спектральными признаками для объекта «карьер»

( x i , x 9 ) , ( x i , x ₈ ) , ( x i , x 7 ) , ( x i , x 5 ) , ( x i , x 4 )

и объекта «пригородная застройка»

( x7

x ₉

) , ( x 4 , x 9

) , ( x 3 , x 9

) , ( ^x 2 , ^x 9

) , ( x i , x 9

) , ( x i , x 8 ) , ( x i , x 7 )

Полученные результаты являются достоверными для всех пар спектральных признаков, так как соблюдается условие |р1 - р2| > Dp при Dp = 0,029 и риске в = 0,025 отвергнуть гипо тезу H0 равенства значений р1, р2 .

а

б

Рис. 2. Фрагменты спутниковой съемки Sentinel-2. Антропогенные территории: а – карьер; б – пригородная застройка

Fig. 2. Fragments of Sentinel-2 satellite imagery. Anthropogenic territories: а – quarry; б – suburban development

а                                         б

Рис. 3. Иллюстрация сильной линейной зависимости между парами спектральных признаков ( x i , x j- ) , характеризующихся оценками коэффициентов корреляции больше 0,9: а – карьер; б – пригородная застройка

Fig. 3. Illustration of a strong linear relationship between pairs of spectral features ( x i , X j ) characterized by correlation coefficient estimates greater than 0,9: а – quarry; б – suburban development

Рассмотрена задача обнаружения антропогенных территорий по спектральным данным.

Ошибка их распознавания в пространстве спектральных признаков x = (xj-, j = 1,9) по обучающей выборке V = (xl, о(i), i = 1, n) равна 0,012, где n = n1 + n2, n1 = 3377 («карьер», o(i) = 1), n2 = 5049 («пригородная застройка», п( i) = 2). При исключении из обучающей выборки, например, спектральных признаков (x4 , x5), (x5, x6), (x4 , x5, x6), оценки ошибок распознавания образов соответствуют значениям 0,011; 0,01; 0,008. Полученное снижение ошибок распознавания образов не является достоверным по сравнению с оценкой ошибки в пространстве признаков Xj, j = 1,9. Однако полученный результат обосновывает возможность сокращения спектральных признаков при синтезе алгоритмов принятия решений и упрощения их оптимизации.

Заключение

Методика проверки гипотезы о независимости пар случайных величин, основанная на использовании непараметрического алгоритма распознавания образов, позволяет обойти проблему дискретизации области значений случайных величин на многомерные интервалы. Эта проблема свойственна общепризнанному критерию Пирсона. Определены условия компетентности предлагаемого метода и критерия Пирсона при анализе однозначных и неоднозначных зависимостей между случайными величинами. С использованием аппарата теории графов предлагаемая методика развита при формировании наборов независимых случайных величин. Полученные результаты обобщены при проверке гипотезы о независимости случайных величин для больших объёмов статистических данных на основе сжатия исходной информации, что позволяет на порядки повысить вычислительную эффективность решаемых задач. Эффективность предложенной методики подтверждена при анализе данных дистанционного зондирования антропогенных территорий и оценивании их состояний. При наличии набора спектральных признаков, характеризующихся сильной линейной зависимостью между его парами, появляется возможность сокращения количества спектральных признаков при распознавании антропогенных территорий с уменьшением оценки вероятности ошибки их распознавания.