Непараметрическая модель в задаче прогнозирования мощности ветряных электрических установок

Энергоэффективность и энергосбережение входят в пятерку приоритетных направлений технологического развития в России. Развивающиеся технологии использования альтернативных источников энергии способствуют рациональному использованию ресурсов и сокращению выбросов парниковых газов [1].

Одним из активно развивающихся направлений в энергетике в настоящее время являются ветряные электрические установки (ВЭУ). Россия обладает колоссальными возможностями для развития ветроэнергетики. В настоящее время на территории России экономически оправдано строительство ветряных электростанций суммарной мощностью до 250 млрд кВт/ч в год. Наиболее перспективными районами являются Дальневосточный регион, Сибирь, Крайний Север, а также территории Алтая, Нижней и Средней Волги, Каспийское побережье и Республика Карелия [2].

Эффективная эксплуатация ветряных электрических установок требует решения проблем, связанных с необходимостью оптимизации режимов их работы в рамках единой энергетической системы. В частности, model allows to optimize the wind power plant operation tree.

возникает необходимость прогнозировать мощность, генерируемую ветряной электрической установкой. Постановка задачи и исходные данные взяты из открытого конкурса Global Energy Forecasting Competition 2012 [3]. Для прогноза выходной мощности семи ветряных электростанций используется следующий набор факторов: метеорологический прогноз, содержащий меридиональную и зональную компоненты скорости ветра (проекции скорости на меридиан и параллель, проходящие через ВЭУ), направление ветра, скорость ветра, и соответствующая прогнозу дата. Исходные данные представляют собой выборку, состоящую из 26 197 наблюдений за четырехлетний период. Прогнозы ветра поступают два раза в сутки, каждый прогноз представляет собой данные о ветре на ближайшие двое суток. По этой причине обучающая выборка содержит многократные прогнозы различной точности. Функционирование ВЭУ сопровождается длительными промежутками отключения или работы на пониженной мощности, связанными как с регламентными работами на станциях, так и с особыми метеорологическими условиями (например, обледенением). Причины каждого конкретного отклонения режима функционирования ВЭУ от нормального неизвестны, поэтому работа с выборкой крайне затруднительна.

Мощность воздушного потока зависит не только от скорости, но и от плотности воздуха [4]. Мы не располагаем данными о параметрах, связанных с плотностью (температура, влажность и т. д.). Однако косвенно они могут быть связаны с порядковым номером дня в году (временем года) и временем суток [5].

Применим деревья регрессии [6] для принятия решения о включении факторов в модель. Построение бинарного дерева представляет собой пошаговую процедуру разбиения подмножеств обучающей выборки на две части гиперплоскостью, перпендикулярной оси выбранного фактора и проходящей через точку разбиения так, чтобы сумма дисперсий выходных значений в получаемых подмножествах была минимальна. Дерево регрессии позволяет последовательно разбивать имеющийся набор данных на подмножества с различными выборочными средними. Таким образом, разбиение по какому-либо фактору свидетельствует об изменении выборочной средней, а следовательно, о наличии некоторой зависимости выходной величины от этого фактора. По этой причине факторы, по которым проводились разбиения, будем считать значимыми.

При построении дерева регрессии определяем следующее правило остановки: любое из полученных в результате разбиения подмножеств должно содержать не менее 500 выборочных значений. Данное правило предотвращает выбор факторов, существенных лишь для небольших подмножеств данных (менее 5 % обучающей выборки).

Дерево регрессии для ветряной станции 1 изображено на рис. 1. В узлах дерева находятся условия, в соответствии с которыми осуществляется бинарное разделение выборки. В конечных узлах дерева указаны значения средних мощностей - выходных величин, соответствующих областей кусочно-постоянных аппроксимаций, которые представляют собой дерево. Первое разбиение было произведено по скорости ветра: для всех первого подмножества скорость ветра меньше 4,9 м/с (верхняя альтернатива), для всех точек второго - больше 4,9 м/с. Каждое из полученных подмножеств было в свою очередь разбито на два подмножества. Процесс продолжается, пока не нарушается требование к размеру минимального листа дерева.

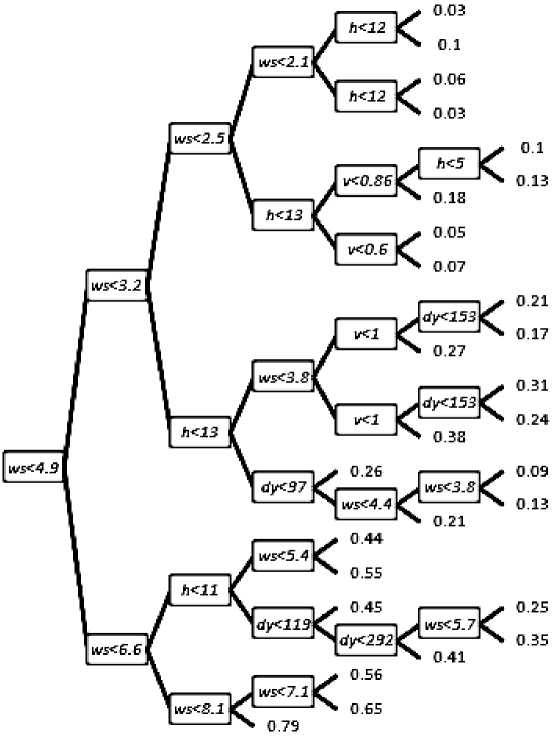
Рис. 1. Дерево регрессии для первой из семи ВЭУ:

верхняя альтернатива - соблюдение неравенств, нижняя - нарушение; ws - скорость ветра; h - час; dy - порядковый номер дня в году; v - зональная компонента скорости ветра

Значимость факторов

Фактор	ВЭУ
	1	2	3	4	5	6	7
Зональная компонента скорости ветра	–	+	+	+	–	+	+
Меридиональная компонента скорости ветра	+	+	+	+	+	+	+
Направление ветра	–	+	–	–	+	–	+
Скорость ветра	+	+	+	+	+	+	+
Год	–	–	–	–	+	–	–
Месяц	–	–	–	–	–	–	–
День месяца	–	–	–	–	–	–	–
Час	+	+	+	+	+	+	+
День в году	+	+	—	—	+	+	+

Для каждого подмножества итогового разбиения была вычислена средняя выходная мощность. Например, при условиях «скорость ветра меньше 2.1 м/с» и «порядковый номер часа в сутках меньше 12» средняя относительная мощность составляет 0,03, а при условиях «скорость ветра меньше 2,1 м/с» и «порядковый номер часа в сутках больше или равен 12» – 0,1.

В табл. знаком «+» отмечены факторы, по которым производились разбиения при построении деревьев для соответствующих ветряных установок (значимые факторы).

Факторы, значимость которых была установлена в процессе построения деревьев регрессий для пяти и более ветряных установок, были включены в модель: x ¹ – зональная компонента скорости ветра; x ² – меридиональная компонента скорости ветра; x ³ – скорость ветра; x ⁴ – порядковый номер часа в сутках; x ⁵ – порядковый номер дня в году. К этому набору факторов последовательно добавлялись скорости ветра в районах соседних установок: сначала фактор x ⁶ должен в наибольшей степени улучшать качество модели, затем фактор x ⁷ выбирается с тем же условием.

После выбора значимых факторов необходимо провести предварительную обработку данных. Электрические генераторы характеризуются монотонно возрастающей зависимостью выходной мощности от скорости ветра. Отдельные фрагменты в обучающей выборке противоречат этому теоретическому результату. Следовательно, предполагается наличие аномалий в измерениях соответствующих величин. Другое предположение заключается в том, что данные в этих областях получены во время нештатного функционирования ВЭУ. Были замечены два типичных случая аномальных данных:

– высокая мощность при слабом ветре;

– низкая мощность при сильном ветре.

Первый случай может быть связан с ошибками в прогнозе погоды; второй – как с ошибками в прогнозах, так и с аномальным функционированием ветряной электростанции. Измерения, соответствующие перечисленным случаям, были исключены.

Прогнозируемую величину (выходную мощность ВЭУ) обозначим y , объем выборки – n . Для предска-

зания выходной мощности использован непараметрический алгоритм k ближайших соседей [7; 8]. Выбор алгоритма обусловлен следующими причинами:

– интерпретируемостью модели. Алгоритм k ближайших соседей позволяет осуществлять прогноз, основываясь на наиболее похожих ситуациях (ближайших соседях) в прошлом в соответствии с выбранным расстоянием. Прогнозирование выполняется простым или взвешенным усреднением выходных значений k ближайших соседей;

– циклическим характером некоторых факторов. Среди факторов, включенных в модель, есть циклические (час и порядковый номер дня в году). Алгоритм k ближайших соседей может работать с ними (в отличии, например, от деревьев регрессии);

– алгоритм не требует повторного обучения при поступлении новых данных.

Поиск ближайших соседей будем осуществлять в соответствии со следующими метриками:

1. Метрика в пространстве одного фактора:

dJ (xp,xJq ) = |xp -j, J = 1, 2, 3, 6, 7, p = 1,2,..., n, q = 1,2,..., n,

где j – порядковые номера признаков, для которых

метрика применима; p и q – порядковые номера наблюдений, упорядоченных по времени их поступления.

2. Метрика в пространстве одного циклического фактора:

– порядковый номер часа в сутках:

d ⁴

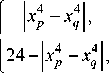
I x 4 — x 4| <  ²⁴ — I x 4 — x^ |x 4 — x 4| ^ ²⁴ — | x 4 — x 4| ,

p = 1,2,..., n ,     q = 1,2,..., n ;

– порядковый номер дня в году:

d 5 ( x p , x q

x 5 _p

q ,

³⁶⁵ — | У

p

q ,

\ xp — x q | <³⁶⁵—| x p — x 5|,

,

I x p — x q | ^ ³⁶⁵ —| x p — x ⁵,

p = 1,2,..., n ,     q = 1,2,..., n .

3. Метрика в пространстве всех факторов взвешенную сумму метрик в пространстве одного фактора:

D ( x_P , ^x_q, w ) = E w^Jd^J ( x p , x q ) . j =1

P = 1,2,..., n, q = 1,2,..., n, где wj – соответствующие различным признакам веса, подлежащие оптимизации в соответствии с критерием качества, который будет рассмотрен ниже.

Модель k ближайших соседей имеет вид [7]:

j ф ( x, x q , w ) y q

У ( x , w ) = q n ---------------,            (1)

E ^ ( X , X q , w ) q =1

где

ф ( X , X q , w ) =

| D ( X , k , w ) - D ( X , X q , w ) , D ( X , X q , w ) ( X , k ) ,

[            0,              D (X, Xq, w )>^( X, k), здесь k - количество соседей, X(X, k) - расстояние между x и k-м ближайшим соседом, yq – выходная мощность ВЭУ для выборочного элемента с индексом q.

Анализ выборочных данных показал, что встречаются ситуации, когда метеорологические прогнозы слабо отличаются друг от друга в течение некоторого промежутка времени. Ближайшие по времени наблюдения, таким образом, будут являться заведомо «хорошими» соседями. Данный эффект приводит к занижению количества ближайших соседей и переобучению при оптимизации модели с использованием критерия Q -кратной кросс-проверки. Идея Q -кратной кросспроверки состоит в выделении в обучающей выборки ( V ) на Q непересекающихся подмножеств случайным

QQ образом (Vt, I = 1,2,..., Q, j V = V, Q V=0), по- i=1                  i=1

строении модели Q раз, при этом каждый раз одно из подмножеств не участвует в построении модели, а используется как тестовая выборка, ошибки Q моделей суммируются [9]:

Q ₂

EE ( y i ^- y ( X , w , V \ V ) ) ^ min,      ⁽²⁾

l=1 i eV                                        w'k где

EL ф ( ^X i , ^X q , w ) y q q =¹

y ( X i , w , V \ V , ) = '------------------ .

E ф ( X , ^X q , ^w )

q =1 X q eV ,

Модель, оптимизированная по критерию (2), будет демонстрировать высокое качество краткосрочного прогнозирования (1…2 ч), однако она будет иметь большие ошибки при долгосрочных прогнозах (до A = 48 ч).

При настройке параметров w и k исключаем A ближайших по времени к проверочному множеству наблюдений из обучающей выборки. Для оптимизации параметров модели (1) был использован следующий критерий:

E E ( y i ^{- y} ( ^X,^w , T , ) ) ² ^ ^min, l ieV ,                                    w , ^k

^V l = ( ( ^X ^ ( l ) , ^y X ( l ) ) , ( ^X ^ ( l ) +1 , ^y X ( l ) +1 ) ,..., ( ^X ^ ( l ) + B -1 , ^y X ( l ) + B -1 ) ) ,

I = 1, 2,..., S - проверочные множества, S - количество проверочных множеств, Х ( l ) = n - S ( A + B ) + + ( A + B )( l - 1 ) , k ближайших соседей отыскиваются из тестовых множеств: T = ( ( X _q , y _q ) : ^ ( X_p , У _р ) e e V l q - p | >  A ) , q = 1, 2,..., n , P = 1, 2,..., n .

Были использованы следующие параметры алгоритма кросс-проверки: B = 36; S = 155.

Для любого w количество соседей k выбиралось методом полного перебора в диапазоне от 1 до 250. Оптимизация по параметрам w выполнялось с помощью модифицированного покоординатного спуска.

С целью улучшения качества модели применялось сглаживание результатов прогнозирования по времени с использованием скользящего среднего:

c

E ^y ( ^X _P + i , w )

y ^{( X} P ) = i =- ‘ 2 c + 1      .                  ⁽³⁾

Ширина окна сглаживания c = 2 была выбрана из условия минимума критерия:

EE ( y i ^{- y} ( ^X ) ) ² ^ min.

l ieVl                               C

Если известны значения мощности ветряной установки в моменты времени P - 2 и P - 1 ( y _{P - 2} и y _{P - 1}), тогда будем использовать их вместо y ( X _{P - 2} ) и y ( X _{P - 1} ) в выражение (2). Процедура скользящего среднего приводит к уменьшению ошибок в модели, связанных с временными сдвигами прогноза погоды.

Модель (3) была проверена на тестовой выборке [2]. Среднеквадратическая ошибка приняла значение 0,147 2. Так как прогнозируемая величина является нормированной, в процентном отношении ошибка составляет 14,72 %. Фрагмент сравнения выборочных значений мощности и выхода модели (3) представлен на рис. 2.

При построении модели были последовательно использованы две процедуры усреднения: вначале – в пространстве факторов, затем – по времени, что привело к сглаживанию прогноза. Тем не менее модель позволяет определить положение практически всех экстремумов функции мощности от времени, а по значению среднеквадратической ошибки предложенная модель на конкурсе [3] заняла второе место.

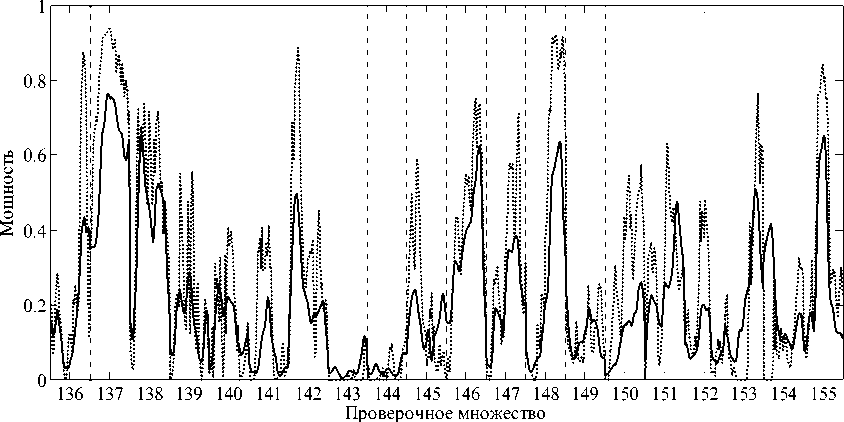
Рис. 2. Сравнение выборки (пунктирная линия) и выхода модели (сплошная линия) для последних двадцати проверочных множеств

Таким образом, построена непараметрическая модель k ближайших соседей. С использованием построенной модели решена задача прогнозирования мощности ветряных электрических установок.

С использованием полученной модели могут быть решены задачи прогнозирования выходной мощности для индивидуальных ВЭУ. Качественный прогноз производства электроэнергии ветряными станциями совместно с прогнозом суточного потребления позволяет минимизировать расходы, связанные с использованием резервных мощностей: снизить сжигание органического топлива, уменьшить общее число вынужденных дорогостоящих запусков и остановок резервных тепловых электростанций. Резервным электростанциям требуется значительное время от запуска до начала генерации энергии. Прогнозирование выходной мощности ВЭУ позволит выводить резервные электростанции на требуемые мощности в случае необходимости заранее.