Непараметрическая оценка кривой регрессии в условиях больших выборок

Работа выполнена в рамках базовой части государственного задания Минобрнауки РФ (СибГАУ № Б121/14).

Вычислительная эффективность непараметрических алгоритмов обработки информации во многом определяется объемом статистических данных и снижается по мере его увеличения, что затрудняет построение систем принятия решений в условиях больших выборок [1; 2].

В подобной ситуации используются принципы декомпозиции исходных статистических данных по их объему и технологии параллельных вычислений. К этому направлению относится смесь непараметрических оценок плотностей вероятности для одномерных и многомерных случайных величин [3–7]. При этом сокращение времени вычислений сопоставимо с количеством составляющих смеси.

Полученные результаты обобщены при оценивании решающей функции в задаче распознавания образов для условий больших выборок. Разработаны двухуровневые непараметрические системы классификации [8; 9]. Установлены асимптотические свойства непараметрических оценок их уравнений разделяющих поверхностей для одномерного и многомерного случаев [10; 11]. Данный подход при восстановлении стохастических зависимостей предполагает разбиение обучающей выборки по её объёму. На этой основе осуществляется синтез семейства частных непараметрических регрессий с последующей их интеграцией в обобщённой модели [12; 13].

Перспективное направление «обхода» проблем больших выборок связано с использованием регрессионной оценки плотности вероятности. Её синтез основан на декомпозиции исходных статистических данных и последующем анализе количественных характеристик получаемого множества случайных величин [14–17].

Цель настоящего исследования состоит в разработке методики синтеза и анализа непараметрических моделей стохастических зависимостей в условиях больших выборок, которая основана на использовании регрессионной оценки плотности вероятности.

Синтез регрессионной оценки плотности вероятности

Пусть имеется выборка V = ( x i , i = 1, n ) из n независимых значений одномерной случайной величины x с неизвестной плотностью вероятности p ( x ).

Разобьем область определения p(x) на N непересе-кающихся интервалов длиной 2р и сформируем множества случайных величин Xj, j = 1, N . В качестве характеристик X j примем частоту Pj попадания случайной величины x в j-й интервал и его центр z j . На основе полученной информации определим элементы выборки V = (z, yj = Pj / (2Р), j = 1, N), где z j центры введенных интервалов и соответствующих им значений оценок y j плотности вероятности. Границы области А изменения случайной величины x априори неизвестны и определяются минимальным и максимальным значениями исходных статистических данных V = (xi, i = 1, n). Поэтому центры интервалов zj, j = 1, N являются случайными величинами и имеют равномерный закон распределения p1 (z ) = (2РN) 1. Объем N полученной выборки V1 значительно меньше объема n исходных статистических данных V. Выборка V1 позволяет оценивание плотности вероятности p(x) свести к задаче восстановления стохастической зависимости.

В качестве приближения по эмпирическим данным V ₁ искомой плотности вероятности p ( x ) примем статистику [14]

NL-f x

• p(x)=c 2PФ|— I,

• j=1

которая является непараметрической оценкой условного математического ожидания

2вNJ УР (x, У) dy -(2)

Здесь и далее бесконечные пределы интегрирования опускаются.

В регрессионной оценке плотности вероятности (1) ядерные функции Ф ( u ) удовлетворяют условиям H :

Ф ( u ) = Ф ( - u ) , 0 <Ф (и) <т , J ф ( и ) du = 1, J и ² Ф ( и ) du = 1.

Коэффициенты размытости c = c ( N ) ядерных функций характеризуют область их определения.

При синтезе p ( x ) в выражение (2) подставляется непараметрическая оценка

• 1 N ^^f x — z j ^f У — У^] 1

p ( x , У ) = ----Ё Ф|-----|Ф|^^1     (3)

ncc 1 j = 1 I c J I C 1 )

совместной плотности вероятности p ( x , y ).

Интегрируя выражение (2) при

• 1    Г      f y - y^j 1                i P^j

• У ф|         | dy = У и У =^Т,

Ci       I c1 )                    2 P получим регрессионную оценку плотности вероятности (1).

В многомерном случае x = ( x v , V = 1 ,k ) стати -стика (1) имеет вид

Nl_k  f j 1

p ( x ) = -2 P j П ^Ф |       I -     (4)

c j = 1     V = 1 I c )

Регрессионные оценки плотности вероятности (1), (4) обладают свойствами асимптотической несмещённости и состоятельности [14]. Из условия минимума асимптотического выражения среднеквадратического отклонения p ( x ) от p ( x ) определена процедура оптимального выбора количества интервалов дискретизации [18; 19]

N = ^А n J p ² ( x ) dx .             (5)

Количество интервалов дискретизации зависит от вида восстанавливаемой плотности вероятности, длины А интервала значений случайной величины и объёма n исходных статистических данных.

Непараметрическая оценка кривой регрессии

Пусть V = ( x i , у , i = 1, n ) статистическая выборка независимых наблюдений одномерных случайных величин ( x, у ), распределенных с неизвестной плотностью вероятности p ( x, у ) и p ( x )>0 V x eQ ( x ). Априори вид однозначной стохастической зависимости у = F ( x ) не задан.

В качестве её модели будем использовать условное математическое ожидание у = ф(x) = ~Т\ I у p(x, у) dy .         (6)

p ( x у

Решающая функция (6) является оптимальной в смысле минимума квадратического критерия [20].

При оценивании p ( x, у ) используем технологию синтеза регрессионной оценки плотности вероятности типа (1). Для упрощения преобразований будем считать, что интервалы значений ( x, у ) одинаковы.

Тогда

N2     (     /Л ( p (x, у) = c^I x-xj U     I,(7)

j = 1       V ^c ) V ^c )

2 N вс г x—x — z2) j I z2 —12 x) =z Ф

⁷⁷ c ^{J J 1} V c J V в

X h । ^ ) p ( t 1 , 1 2 ) p ( Z 1 , Z 2 ) dt 1 ... dz 2 , где M - знак математического ожидания.

Осуществим замену переменных ( z 1 - 1 1 )/ в = и 1 , ( z ₂- 1 ₂)/ в = и 2 . С учетом p ( z 1 , z ₂) = (2 в N )² получим

M ( ф ( ^x ) ) = N ^ J. J ( ^{в и} 1 ⁺ t 1 ) ^ф| x ^в u ² t ² 'I ^X 2 c ^J °              V c )

=^ J [J t ^I

2 c ^{J J J}     V

x h(и2) h(u1) p(t1,12) du1...dt2 = x — в и 2 — t 21X c )

x h ( и ₂ ) p ( t 1 , 1 ₂ ) du ₂ dt 1 dt ₂.               (9)

Обозначим ф ( 1 ₂) = M ( 1 1 / 1 ₂). Проведём замену ( x - в и ₂- 1 ₂)/ c = и . На этой основе преобразуем (9) к виду

M (ф (x)) = Nв JJ ф(x — ви2 — cu) x x ф(и) h(и2) p(x — ви2 — cu) du du2

где N ² - объем массива данных ( x^j , у^j , P ^j , j = 1, N ² ) , формируемых на основе исходной статистической выборки V = ( x i , у^- , i = 1, n ) .

Значение P^j определяет частоту встречаемости наблюдений из V в элементе ( x^j ± в , у⁷ " ± в ) равномерной сетки в пространстве ( x , у ).

Тогда с учетом p I у | = p (x, у) = 2 n в p (x, у)

V x )    p ( x )

непараметрическую оценку (6) представим в виде

Разложим функции ф ( x - в и ₂- cu ), p ( x - в и ₂- cu ) в ряд Тейлора в точке x . Тогда при достаточно больших n

приходим к утверждению

M ( ф ( x ))~ ф ( x )

Г ф ( x ) p ⁽²⁾( x )

V    ² p 1⁽ x )

у = ф ( x ) = 2^ ^у^- P^- ф ^c i = 1

x — x i

.

c

Исследуем свойство асимптотической несмещённости статистики (8). Пусть функции ф ( x ), p ( x, у ) ограничены и непрерывны со всеми своими производными до 2-го порядка включительно. Ядерные функции Ф ( и ) удовлетворяют условиям H .

Определим частоту появления случайных величин в виде

nj pj = ¹ yh I x_ n ^E V

в

- I h I ^у-

в

где

yi

,

к \ /1 V|u £ 1, h (и) = v } [0 V | и |> 1.

Наблюдения из выборки ( x i , yⁱ ) , i = 1, n

имеют

один и тот же закон распределения p ( z 1 , z ₂). Элементы массива данных ( x ^j, у ^j ) j = 1, N ² характеризуются плотностью вероятности p ( t 1 , 1 ₂).

Тогда

p ( x ) Гв ²     ₂)

+ I + c I X p 1⁽ x ) V ³       )

+ ф ⁽¹⁾( x ) p ⁽¹⁾( x ) p 1^{( x} )

+ ф ⁽²⁾( x ) p ( x ) I +

^{ф( )( x} ) ^{p ( )( x} ) в ² + O ( c 4 , p 4 , c ² в ²).      (10)

Статистика (8) обладает свойством асимптотической несмещенности по отношению к оптимальному решающему правилу (6), если закон распределения исходной выборки наблюдений x равномерный, т. е. p ( x ) = p 1 ( x ). Это возможно при проведении активного эксперимента при исследовании зависимости у = F ( x ).

Для устранения смещения необходимо умножить статистику (8) на отношение p 1 ( x ) / p ( x ). В результате получим

NN-

_ E у^{- а} i ^{( x} )            _{f A}

Y i I

^{ф( x} ) = -Ny ------, a - ( x ) = P ф^ I . (11)

E a i ( x )               ^V c ⁾

i = 1

В многомерном случае при x = ( x 1 , ^, x k ) непараметрическая регрессия имеет вид N ^{k + 1}

_ E у^{- a} i ( ^x )             _k .

^{ф( x} ) = ^J N +1------- , a i (x ) = P i 1П фГ x v^- x v-

E a(x)              v=1 V cv i=1

Анализ результатов вычислительных экспериментов

Исследовались свойства непараметрических моделей типа (8), (10) и традиционной непараметрической регрессии [20] методом вычислительного эксперимента. Исходные данные ( x i , y i , i = 1, n ) формировались в соответствии с примером работы [21]

y = F ( x ) = 1– x +exp(-200( x -0,5)²).        (12)

Значения yi вычислялись по формуле yi = F(xi)+2(0,5-6i) F(xi) r, i = I?n.

Случайная величина se [0; 1] имеет равномерный закон распределения, а r – уровень помех.

Оценка эффективности изучаемых моделей определялась критерием

W = £т F(xVH(j

>j    F (xj)    ’ где m – объём контрольной выборки.

При построении непараметрических моделей в качестве ядерных функций использовалось ядро В. А. Епанечникова [22].

I 3 _- 3 u u ф ( u ) = Ь>/5 uoV5

I o v |u| < V5

v | u | > V5.

Вычислительные эксперименты при фиксированных условиях исследования повторяются 20 раз. По полученным результатам вычислялись ошибки аппроксимации W*, t = 1,20 и среднее W их значение.

Установлено, что объём исходной выборки n может быть сокращён на порядок и выше. На такую же величину повышается вычислительная эффективность непараметрической регрессии. Обнаружена линейная зависимость между значениями уровня помех r и количеством N интервалов дискретизации.

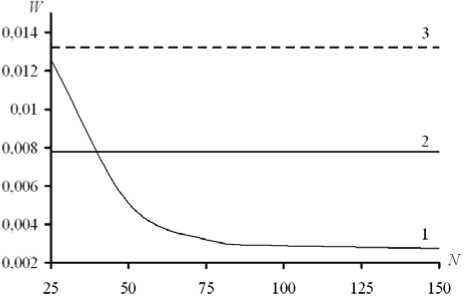
Зависимость средней относительной ошибки аппроксимации W от количества интервалов дискретизации N при n = 10000, r = 0,05: кривая 1 соответствует модели ф ( x ) (11); прямые 2 и 3 характеризуют традиционную непараметрическую регрессию при объёме обучающей выборки n = 500 и n = 200

Точность аппроксимации непараметрической регрессии ф ( x ) (11) выше в два и более раза, чем со смещением (8). Традиционная непараметрическая регрессия менее устойчива к уровню помех.

С ростом количества N интервалов дискретизации аппроксимационные свойства статистики (11) улучшаются, что согласуется с результатами аналитических исследований (см. рисунок). Данный факт особенно проявляется при высоком уровне помех.

Непараметрическая модель стохастической зависимости (11) является эффективным средством обработки данных большого объема. Ее синтез осуществляется путем декомпозиции исходной статистической информации и анализа количественных характеристик, получаемых множеств случайных величин. На этой основе осуществляется «сжатие» исходных данных. Предлагаемая статистика обладает свойством асимптотической несмещенности.

По своим аппроксимационным свойствам и устойчивости к помехам она значительно превосходит традиционную непараметрическую регрессию. Особенность структуры разработанной непараметрической модели стохастической зависимости позволяет решить проблему её доверительного оценивания.