Непараметрическая оценка смеси плотностей вероятности, основанная на технологии размножения статистических данных

Большинство статистических методов обработки информации ориентировано на представительные обучающие выборки. Однако при решении прикладных задач часто имеется ограниченный объем наблюдений - короткая либо малая выборка, что обусловливается неста-ционарностью объекта исследования, высокой стоимостью и сложностью получения дополнительной информации. Получаемые на их основе решающие правила не всегда обеспечивают приемлемые результаты, так как информации малых выборок недостаточно для оценивания вероятностных характеристик изучаемых закономерностей.

Проблемы малых выборок можно разрешить с помощью технологий обработки информации, основанных на бутстреп-методах. Ниже на основе результатов аналитических исследований будет обоснована эффективность его применения при непараметрическом оценивании плотностей вероятности.

Синтез непараметрической оценки смеси плотностей вероятности, основанной на технологии бутстреп-мето-да. Пусть V = ( x i , i = 1, n ) - выборка из n независимых наблюдений случайной величины x = ( x _v , v = 1, k ) с плотностью вероятности p ( x ), вид которой априори неизвестен.

Сформируем на основе исходной выборки N групп наблюдений выборку V j = ( x i , i е I j ) , где I j - множество номеров элементов из V , составляющих j -ю группу Количество элементов в группах одинаково и равно n = n - n'. Каждая пара групп V j , V t , j , t = 1, N , j * t отличается n' элементами. Количество групп элементов N = n/n '.

По каждой выборке V_j построим непараметрические оценки плотностей вероятности [1; 2]:

ki

Pj( x)=-4- ЕПф^   '|, nПcv-Ijv = v cv v         (1)

v =1

j = VN, где ф(u) - ядерные функции, удовлетворяющие условиям H:

Ф ( и ) = Ф ( - и ), 0 <Ф ( и ) <да , j Ф ( и ) du = 1, j и ² Ф ( и ) du = 1, j и^т Ф ( и ) du <да , 0 <  m <да ;

c_v = c v ( n ) - коэффициенты размытости ядерных функций, значения которых убывают с ростом n . Здесь и далее бесконечные пределы интегрирования опускаются.

В качестве приближения p ( x ) по статистической выборке V пр имем смесь непарам етрич еских оценок p j ( x ) плотности вероятности

p ^{( x} )    _XZ Pj ^{( x} )•                 ⁽²⁾

N j =1 ^j

Статистика (2) построена в соответствии с бутстреп-методом и допускает использование технологии параллельных вычислений.

Исследуем асимптотические свойства оценки плотности вероятности (2) в условиях, когда k = 1 .

Теорема . Пусть p ( x ) и первые две ее производные ограничены и непрерывны; ядерные функции φ ( и ) удовлетворяют условиям нормированности, положительности и симметричности H ; последовательность c ( n ) = c коэффициентов размытости ядерных функций такова, что при n ^ да значения c ^ 0, а при nc ^ да и ¹ ^ 0 , n n'

^ 0 . Тогда при конечных значениях N непарамет-n              _ рическая оценка p(x) смеси плотности вероятности p(x) обладает свойством асимптотической несмещенности и состоятельности.

Д о к а з а т е л ь с т в о. По определению

M ( Р ^{( x} ) ) = N ^х

N            1     ( - - t^

^X Z M ( P j^{( x} ) ) = -j ^Фl — I p ⁽ t ) ^dt = j =1                 c v c /

= j Ф ( и ) p ( x - cu ) du , где M - знак математического ожидания.

Разлагая p ( x - cu ) в ряд Тейлора и ограничиваясь первыми двумя членами ряда при n ^ да , имеем

W = M ( p ( x ) - p ( x ) ) ~ ^Р ₂ ^{( x} ) c²,         ⁽³⁾

где p ⁽²⁾ ( x ) - вторая производная плотности вероятности p ( x ) по x . Отсюда из условия c = c ( n ) и c ^ 0 при n ^ да следует свойство асимптотической несмещенности непараметрической оценки смеси плотностей вероятности (2).

Для доказательства сходимости p ( x ) в среднеквадратическом отклонении рассмотрим выражение

M J ( p ( x ) - p ( x ) ) dx =

Г 1 N*,           J2

= MJ IfZ(P(x’-Pj(x’) dx =

L N j =1                   _

Отсюда, пренебрегая величинами малости 0 Np |,

0 I — I , получим I n ² J

n

= ^ M

N ²

N                      2

ZJ ( p ^{( x} ’ ^- p j ^{( x} ’ ) dx + j =1

NN

+ZZJ( p(x’- pj( x ’)x j=11=1 t # j

x ( p ( x ) - p_t ( x ’ ) dx

M J ( p ( x ’ - p ( x ’ ) dx

II ф( и ’IP x

_x ^r 1 + ( n - n 9 ( N - 1) ¹+ c 4

n

N n c

II p ^<2’⁽ x ’|p

.

Найдем асимптотическое выражение функционала

M J ( p ^{( x} ) ^- p j ^{( x} ) ) ( p ^{( x} ) ^- p, ^{( x} ) ) dx = = J p ² ( x ) dx - M J p_t ( x ) p ( x ) dx -

- M J p j ( x ) p ( x ) dx + M J p j ( x ) p t ( x ) dx .       (5)

Преобразуем его последнее слагаемое:

M J p j ( x ) p_t ( x ) dx =

= —2 2 n c ^J

xi

+

£ M Ф ²

' ^E In

c

+ £ £ M ^ф

' E I j VE I t \ I j

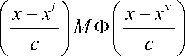
dx ,

которое при дос таточ но большом объеме n элементов в

группах V j , j = 1, N , может быть представлено в виде n - n 'lias / \l|2 n ^{2 -} ( n ^- n ') -2^ |^ф ( u )| +---- n i---

x J ( p ( x ) + c ² p ^<2,( x ’/2 ) dx ,           ⁽⁶⁾

где ||Ф ( и )| |² = J ф ² ( и ) du .

Заметим, что при n ^ да

M J p t ( x ) p ( x ) dx ~ || p ( x )||² + ^ J p ^<2’( x ) p ( x ) dx , где || p ( x )|| = J p ² ( x ) dx . Тогда асимптотическое выражение для функционала (5) соответствует выражению

1^ |Ф( и Ц2 + £.|p«( x J +

-n _ c ,                                       (7)

+ ” _ Y J ( p ( x ) + c ² p ^<2,( x ’/2 ) dx .

С учетом (7) и справедливости при n ^ да утверждения [2]

m к p ( x ) - p ( x ) ) ² dx ~ is u f + c *l l ^{p ,} ₄ ¹⁽ x ’ll’ , запишем асимптотическое выражение для (4):

^M J ( p ^{( x} ’ ^{- p ( x} ’ ) ^{2 dx} ~ N^x

II^ф( u ’IP + ^{c 4}1l ^{p <2)( x} ’f ' _c         4

Нетрудно заметить, что при выполнении условий c ^ 0 , _c ^ да при n ^ да оценка плотности вероятности (2) сходится в среднеквадратическом отклонении к p ( x ’, а с учетом свойства ее асимптотической несмещенности является состоятельной.

Сравнение асимптотических свойств статистики (2) и непараметрической оценки Розенблатта-Парзена. Определим минимальное зн а чение W ₂ выражения (8) при оптимальных значениях c коэффициентов размытости ядерных функций непараметрических оценок p j ( x ’, j = 1, N , составляющих их смесь p ( x ) (2).

В принятых допущениях значение

Тогда

W 2 =

c =

IIф( u ’IP ^ n||p <2’( x ’||2

1^{Ф( u} ’ll^:

n - n ‘

I 1 Гз n x — 1 + —

INI

1^{Ф( u} ’ll'

n - n ‘

.

214..

L I p ^<2’⁽ x ’I

- n ‘

n

2Y

L   I p ^<2’( x )|²

I n

-

n

n' Г|

-⁺₄ J .     (9)

Если n' = 0 , то W₂ совпадает с минимальным значением асимптотического выражения среднеквадратичес-

кого отклонения

W ₂‘ -

= 5 П^с и иР I ⁴

n

II p ^<2’^{( x} ’||²

для оценки плотности вероятности типа Розенблатта-Пар-зена

n p (x ’ = — £фр nc i=1 I.

- x '

c

при оптимальных значениях c = c * . При этом

W2 = 41_

W ₂ ‘ = 5 I n

n 1 ⁵ Г n

-

-

n ‘

n

n' 1

— + -

.

По аналогии сравним главные дисперсионные составляющие

W 3

= n - n' Р||Ф(и)|Р 1

N-1 +--

N

n - n'llA( ^l|2   c4 I|p<2>(x’f

|ф(u’ll + И 4 И +

+ n _₂ n J ( p ( x ) + c ² p ^<2’( x ’/2 ) dx

n

w ; =

n - n ‘

1|^{ф( u} ’ll'

n

II p ^<2’^{( x} ’||²

- ||p ^<2’⁽ x ’||²

,

непараметрических оценок плотностей вероятностей (2), (10). Их отношение будет следующим

W 3

W 3

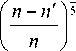
Так как объем статистических данных при синтезе составляющих (1) статистики (2) меньше, чем при формировании непараметрической оценки плотности вероятности (10), то очевидно, что ее смещение меньше по сравнению с оценкой плотности вероятности (2). Действи- тельно, отношение их минимальных асимптотических выражений смещений при оптимальных значениях коэф- фициентов размытости имеет вид

W 1

W 1

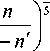
> 1.

Значения отношений (11), (12), (13) при n ' = a n приведены в таблице.

Использование статистики (2) позволяет несколько улучшить эффективность оценивания плотности вероятности по сравнению с оценкой Розенблатта–Парзена (10).

С уменьшение м n' = a n растет количество групп наблюдений V j , j = 1, N , но снижается уровень их разнообразия. При этом состав групп наблюдений незначительно отличается. Поэтому в данных условиях аппроксимационные свойства статистик (2) и (10) практически одинаковы.

При увеличении n' уменьшается количество составляющих смеси непараметрических оценок плотностей вероятности (2), что приводит к снижению ее аппроксимационных свойств, несмотря на рост разнообразия групп наблюдений Vj, j = 1, N. При этом уменьшение дисперсии смеси (2) объясняется различными темпами изменения значений ее смещения и среднеквадратического отклонения от искомой плотности вероятности.

Таким образом, использование технологии бутстреп-метода позволяет повысить эффективность оценивания плотностей вероятности. Получаемые при этом непараметрические оценки смеси плотностей вероятности обладают повышенными аппроксимационными свойствами, что особенно наблюдается в снижении их дисперсии и среднеквадратического отклонения. Определены условия их асимптотической сходимости и преимущества перед традиционной непараметрической оценкой Розенб-латта–Парзена. Следует ожидать более значительного преимущества предлагаемой методики оценивания плотностей вероятности в условиях малых выборок.