Непараметрическая оценка условной плотности распределения вероятности в задаче управления статическим объектом

Описывается один подход к решению задачи управления стохастическим статическим объектом с одним входом и одним выходом. Предполагается, что параметрическая структура модели объекта и законы распределения помех неизвестны. Информация об объекте управления содержится в выборках измерений «вход-выход».

Под управлением понимается процесс выведения объекта в требуемое состояние посредством выбора соответствующего входного воздействия. В классической теории управления, как правило, рассматриваются задачи управления динамическими процессами. Однако на практике достаточно часто встречаются объекты, описание которых в виде системы дифференциальных, интегро-дифференциальных или конечно-разностных уравнений невозможно по тем или иным причинам. Например, такая ситуация может возникнуть из-за несовершенства средств контроля входных и выходных величин, недостатка измерений для анализа «динамики» процесса или сложности описания переходных процессов, происходящих в объекте. В этих случаях исследователь вынужден рассматривать объект как статический с запаздыванием.

Постановка задачи управления предполагает наличие, во-первых, некоторой модели объекта и, во-вторых, цели управления. Анализ задач управления статическим объектом показывает, что основными типами целей управления являются: а) стабилизация выхода объекта, т. е. приближение выхода объекта к желаемому значению с заданной точностью; б) оптимизация выхода объекта, т. е. приближение некоторой скалярной функции выхода к своему минимальному (максимальному) значению с заданной точностью [1]. Формально задачи оптимизации можно свести к задачам стабилизации, и наоборот.

Один из подходов к решению задачи управления статическим объектом предполагает построение так называемой инверсной модели объекта [2]. Например, для объекта с одним входом и одним выходом основной инверсной характеристикой является регрессия. На основе использования непараметрических оценок инверсных регрессий в дальнейшем строятся алгоритмы адаптивного управления при априорной неопределенности.

Однако построенная таким образом инверсная модель не способна учитывать многозначность получаемых характеристик «выход-вход» объекта. На практике зачастую мы имеем дело с неоднозначностью в выборе управляющего входного воздействия, приводящего объект управления к желаемому состоянию. Кроме того, различные альтернативы могут существенно различаться по стоимости или степени целесообразности их реализации. Целью настоящего исследования является повышение эффективности управления статическим объектом, учитывая проблему многозначности характеристик в процессе выбора управляющего воздействия.

Пусть объект управления относится к классу нелинейных статических с одним входом и одним выходом (рис. 1):

Рис. 1. Структурная схема объекта управления

На рисунке приняты следующие обозначения: ОУ - объект управления, и - входная переменная объекта, x - выходная переменная объекта, ^ - случайное воздействие на объект, h ^x - аддитивная помеха в канале измерения выходной переменной ( M { h x } = 0, D{h ^x } <^ ).

Имеется выборка статически независимых наблюдений входной и выходной величин { u_t , x i },i = 1,2,..., 5 . Требуется решить задачу стабилизации, т. е. найти такое управляющее воздействие, которое приводит к желаемому значению выходную переменную. Таким образом, необходимо по имеющимся априорным сведениям и выборке измерений { u i , x i } отыскать множество { U j }, для которого справедливо x ( U j ) ® x * ,( j = 1,2,...).

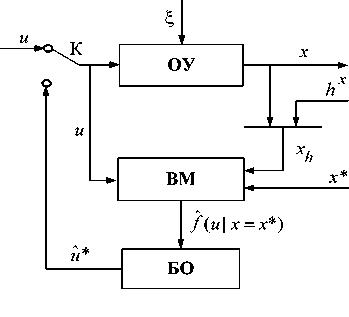
Рис. 2. Структурная схема процесса управления

Для решения поставленной задачи предлагается подход, основанный на построении вероятностной модели объекта, которая может быть получена путем непараметрического оценивания условной плотности распределения вероятности [3]. Затем задача сводится к нахождению мод условного распределения, т. е. наиболее вероятных значений входной переменной при условии фиксированной выходной переменной. В частности, в непрерывном случае необходимо отыскать максимумы условной плотности распределения вероятности. Так как рассматриваются многозначные характеристики, следовательно, желательно оценить все локальные моды оценки условной плотности. Таким образом, искомое множество значений входной величины { u_j } определяется в результате решения задачи оптимизации:

f(uu | x = x * ) ^ max.               (1)

u

Схематически процесс управления объектом представлен на рис. 2.

f ( u | x = x * )

1 L - к sM c sx

s

Г L к cs» i=1

*

x

xi

c sx

1 L - к sM c sx

x

- ^x i

)

к

s

L к i =1

x - x i

- к u:^ c c

7 ^s u V ^s u

*

x

xi

A

A

7

c s _x

u - ui

7

где K ( z ) – ядерная функция, удовлетворяющая следующим условиям:

• 1)    к ( z ) <«, V z G к ( z ),

• 2)    J к ( z ) dz = 1,                     (4)

n ( z )

• 3)    J к ²( z ) dz <« .

n ( z )

На рисунке к введенным ранее обозначениям добавляются следующие: ВМ – вероятностная модель объекта управления, БО – блок оптимизации построенной оценки, x * – желаемое значение выходной величины, f ( u | x = x *) - оценка условного распределения, u ˆ * – управляющее воздействие, К – переключатель, переводящий систему из режима накопления информации в режим управления.

Условная плотность распределения вероятности f ( u | x ) является наиболее полной характеристикой, устанавливающей связь между случайными величинами X и U . Зная её, можно вычислить любые другие условные характеристики объекта [2; 4; 5]. Условная плотность выражается через безусловные плотности из формулы умножения плотностей:

f ( u | x ) = f ( u , x )/ f ( x ). (2)

В [2; 4] предлагалось заменить безусловные плотности в (2) непараметрическими оценками плотности Розенблатта–Парзена [5; 6]. В результате получаем непараметрическую оценку условной плотности распределения вероятности:

Оценка (3) включает параметры c и c . Пара-ux метр csu определяет ширину диапазона, в котором наиболее вероятно наблюдаются искомые значения входной переменной, при этом варьирование значения csu в широких границах не оказывает существенного влияния на точность получаемых результатов. Параметр отвечает по большей части за «степень размытия» мод непараметрической оценки условной плотности распределения.

Значение c определяет степень «гладкости» x оценки в целом. «Гладкая» оценка облегчает оптимизацию критерия (1), однако при этом может снижаться точность отыскания искомого управления. Чрезмерное сглаживание приводит к исчезновению некоторых существенных локальных максимумов критериальной функции. Вместе с тем csx определяет точность выполнения условия x = x*, поэтому увеличение csx приводит к снижению точности достижения цели управления.

Для обеспечения надежности нахождения решений предлагается осуществить переход от исходной выборки наблюдений входных и выходных величин к новой выборке, заданной в узлах «равномерной сетки» в пространстве входных переменных. Такой переход достижим различными способами, в частности, с применением непараметрической оценки регрессии.

Исходная выборка наблюдений входной и выходной величин обозначается { u i , x i },i = 1,2,..., s . Задаём «равномерную сетку» в пространстве входных переменных с количеством узлов s . Шаг дискретизации для сетки вычисляется следующим образом:

max{ u i } - min{ u i }

A u, = —ii ------; i = 1,2,..., s ; j = 1,2,..., J. (5)

j

s

Вычисляем новые «выборочные» значения

{ U j , x j }, j = 1,2,..., 5 по формулам

U j = min{ u i } + j A u j ;

^{x ( u} j ) = x j

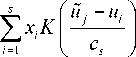
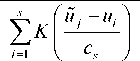
где c₅ - оптимальный параметр размытости для непараметрической оценки регрессии, который определяется в процессе оптимизации среднеквадратичного критерия:

s

W ( С ) = - X

5 i = 1

s

X XjK j=1 j * i

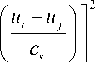
xi

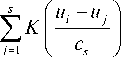
j * i

^ min.

c _s

плотности, указав границы интервалов, в которых они находятся, а затем применить на каждом интервале один из методов локальной оптимизации.

Локализовать основные моды оценки условной плотности распределения можно с помощью эвристической итерационной поисковой процедуры. Обозначим через [ a g , b g ] границы интервала входной переменной, в котором содержится хотя бы одна мода условной плотности (3). Введем поисковую добавку A , удовлетворяющую следующим условиям:

0 < A <  a g , A = 0,005 ■ c_Su . Поиск осуществляется с левой границы a g до тех пор, пока a g <  b g . На первой итерации ( к = 0) присвоим u_k = a g . Левая граница a интервала, в котором содержится один из искомых локальных максимумов, определяется следующим образом.

Если (( f ( u_k | x ) = 0 и f ( u_k + A | x ) >  0)) ^

^ a = u_k ; иначе u_{k + 1} = u_k + A .

Переход к «равномерной сетке» позволяет дополнительно сгладить непараметрическую оценку условной плотности распределения. Однако при реализации такого подхода возникают трудности, связанные с пропуском данных. Особенно эта проблема будет актуальна в условиях малых выборок, когда разрывы между измерениями могут быть значительными. В местах пропуска данных непараметрическая оценка (6) обратится в неопределенность. В некоторых случаях это может повлечь за собой появление новых «ложных» решений, которые помешают достичь заданной цели в процессе управления.

Для преодоления возникших трудностей предлагается представить непараметрическую модель (6) в виде агрегата из двух величин:

M(X | и ) = { x( u ), Q ( и )}, (8)

Поиск правой границы b локального интервала осуществляется с помощью аналогичной итерационной процедуры, начиная с найденной границы a :

Если (( f ( u_k | x ) >  0 и f ( u_k + A | x ) = 0)

^{или (} f ^{( u} k ^{— A|} x )> ^{f ( u} k I x ))

^и f ^{( u} k ^{+A| x} ) >  ^{f ( u} k | ^x ))) ^ ^b = ^u k ;

иначе u_{k + 1} = u_k + A .

где x ( u ) - оценка регрессии; Q ( u ) - логическая переменная, которая принимает значение, равное единице, если в окрестности u имеются наблюдения, и, соответственно, ноль, если выборочных данных в окрестности нет. Впервые этот подход рассмотрен в [7; 8].

Непараметрическая оценка регрессии строится на основе исходной выборки в узлах «равномерной сетки». Следовательно, в этих узлах необходимо проверить наличие пропусков выборочных данных. Для этого введем в рассмотрение следующую индикаторную функцию:

После локализации всех максимумов оценки условной плотности распределения на каждом соответствующем интервале применяется один из методов одномерной оптимизации. В результате получаем искомое множество { u j .} значений входной переменной, доставляющее решение задачи стабилизации.

Было предложено использовать оценку производной условной плотности распределения. Непараметрическая оценка производной от условной плотности распределения вероятности будет иметь следующий вид [4]:

f (u | x = x )

K а—Ъ

' С

⁵du     V ^sdu

A

7

Q ( u ) = <

1           ¹ V¹ \\ ^u

1, если - X K I —

5 , = 1 I

1 X - k

5^ c

*

x - x i

cs

и I

- 1> 0

0,

s

X K

^C 5du i = 1

* x

^{- x}i

. u — ui

c

V  5du 7

иначе.

Важнейший этап решения поставленной задачи -оптимизация многоэкстремального критерия (1). Предполагается, что в одномерном случае возможно локализовать основные максимумы оценки условной

s

X K i=1

Если гарантировать унимодальность оценки условной плотности для каждого локального интервала,

тогда для u , принадлежащего этому интервалу, необходимо решить уравнение с единственным корнем:

‘                    *

f ( и | x = x ) = 0 .               (13)

Оценка (12) содержит параметр c_sdu . Параметр c_sdu определяет ширину диапазона, в котором наиболее вероятно содержится решение уравнения (13), при этом значение c_sdu в широком диапазоне не оказывает существенного влияния на точность получаемого решения.

Для численного решения уравнения (13) выбран метод Эйлера, в котором стандартная процедура метода была модифицирована добавлением дополнительного уточняющего условия. Вычислительная процедура алгоритма решения уравнения с единственным корнем на локальном интервале [ a , b ] состоит из двух шагов.

На первом шаге вычисляется значение uk+i = uk + gf'(uk | x = x*),            (14)

где u_k – текущее решение; g – коэффициент, отвечающий за скорость сходимости.

На следующем шаге происходит анализ знака оценки производной:

Если ^{(( f} ' ( u k + i | x ) >  ^{0 и f} ' ( u k | x ) <  ⁰⁾

или (f ' ( u k + i | x ) < ^{0 и f} ' ( u k | x ) > ⁰⁾⁾ ^ g = ^0, 5 - g .

Затем происходит возврат к первому шагу. Условием остановки итерационной процедуры служит достижение заданной точности решения £. В результате выполнения алгоритма для всех найденных ин- тервалов получаем искомое множество {uj} значений входной переменной.

При реализации такого подхода удается достигнуть большей скорости сходимости алгоритма к решению, чем в случае максимизации критериальной функции (1), что становится возможным за счет внедрения дополнительного коэффициента g .

Описанный выше подход к решению задачи стабилизации нелинейного статического объекта был реализован в виде программной системы на языке C++ Builder 6. В представленной реализации алгоритма рассмотрен объект, у которого связь между входной и выходной переменной задана кубической параболой x = 0,005 и ³ - 0,015 и ² - 1,35 и + 10. Для одномерной оптимизации на локальном интервале был использован метод деления отрезка пополам.

В рабочем окне программы (рис. 3) пользователь может задавать основные параметры алгоритма, закон распределения и дисперсию помехи в канале измерения выходной переменной, а также необходимую точность получаемых результатов.

Алгоритм управления был многократно протестирован при различных параметрах. В качестве показателя надежности ^ алгоритма было принято соответствие количества найденных решений истинному их количеству. По результатам серии экспериментов подтверждение получил тот факт, что ключевым настраиваемым параметром алгоритма является значение коэффициента csx . Критерия для выбора оптимального параметра c не существует, так как поста-x новка задачи предполагает отсутствие вида истинной характеристики объекта управления.

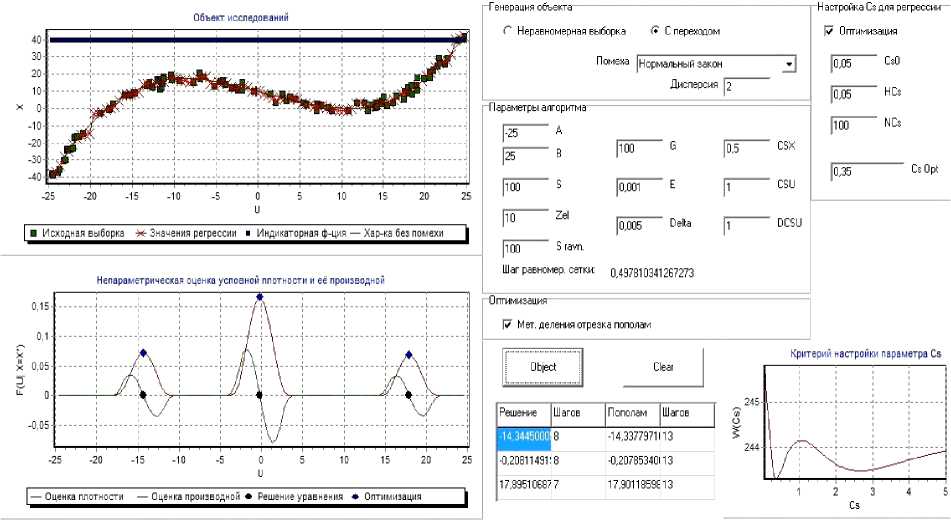
Рис. 3. Рабочее окно программной системы с результатом работы алгоритма

Основное внимание при анализе работоспособности предложенного алгоритма уделялось экспериментам с выборками малых размеров, что является особенно актуальным для использования алгоритма на практике. Вначале алгоритм был протестирован при отсутствии помехи в канале измерения выходной величины. Входное воздействие выбиралось случайным образом на интервале [–25, 25]. Исходная выборка наблюдений за объектом управления была выбрана объемом 5 = 100. После стократного запуска при различных выборках было установлено, что для c₅ x <  0,25 надежность работы алгоритма управления V составила ® 60%, а для 0,25 <  с, <  5 -100 %. s _x

Однако стоит отметить, что при достаточно высоком значении параметра c ухудшается точность найден-x ного решения уравнения (13).

Далее алгоритм управления был протестирован при добавлении значительной помехи в канале измерения выходной переменной: h x = 20 %. По-прежнему рассматривается случай малой выборки исходных наблюдений за объектом. По результатам многочисленных запусков на различных выборках было установлено, что для c₅ x <  0,25 надежность V алгоритма <  50 %, для 0,25 <  c₅ x <  1 - ® 70 %, а если 1 <  с₅ <  2 - ® 80 % . При увеличении объема исходной выборки до 5 = 200...300 надежность нахождения решений в случае 20%-й помехи составила 100 %.

Проведенные исследования показывают, что преимущество описанного выше алгоритма для решения задачи управления стохастическим статическим объектом заключается в высокой надежности нахождения решений для неоднозначных характеристик при малых объемах выборки и значительной помехи в канале измерения выходной величины. К недостаткам предложенного подхода относится отсутствие критерия для выбора параметра c , который в большей степе-x ни, чем все остальные параметры, отвечает за точность результатов, а также за количество найденных альтернатив при неоднозначности в выборе входного воздействия.