Непараметрическая регрессия в условиях частичных сведений о виде восстанавливаемых закономерностей

Для наиболее полного учёта априорной информации о виде восстанавливаемых зависимостей и экспериментальных данных о её локальном поведении широко используются гибридные модели [1]. Традиционные гибридные модели сочетают в одном решающем правиле преимущество параметрических и непараметрических аппроксимаций. При этом единое решающее правило образуют параметрическая модель восстанавливаемой зависимости и корректирующая её функция непараметрического типа, которые строятся в одном и том же пространстве переменных. Полученные результаты были развиты для условий наличия частичных априорных сведений о виде восстанавливаемых зависимостей в ограниченном пространстве признаков [2]. Основная проблема применения гибридных моделей состоит в выборе вида корректирующей функции, которая является трудно формализуемой. Для её обхода предлагается использовать непараметрическую регрессию, синтез которой основан на обобщении априорной информации о виде восстанавливаемых зависимостей и экспериментальных данных об их локальном поведении.

Цель работы состоит в обосновании возможности учёта априорных сведений о виде восстанавливаемых закономерностей при синтезе непараметрических моделей стохастических зависимостей, основанных на оценках плотности вероятности типа Розенблатта-Парзена [3].

Синтез модифицированной непараметрической регрессии. Пусть об искомой однозначной зависимости у = v(x) V x e Rk (1) известно её описание у = F(X1, a) V x e Rk2, k2 < k относительно некоторого ограниченного набора признаков из x = ( x1, x), x1 =( x1 v, v = 1, k 1), k = k 1 + k2 и выборка V = (xV, v = 1, k , y', i = 1, n) эксперимен тальных данных, составленная из статистически независимых значений переменных x, у исследуемой зависимости (1). Параметры a полинома F (xy a) заданы.

Задача состоит в построении модифицированной непараметрической модели у ( x ) зависимости (1), совмещающей в одном решающем правиле всю имеющуюся априорную информацию.

На основании исходных экспериментальных данных сформируем промежуточную обучающую выборку

V* = ( x ' , У = F ( x ' , a ) , У , ' = 1, n ) .

Принимая в качестве оптимального решающего правила, в смысле минимума среднеквадратического отклонения, условное математическое ожидание ф ( x ) [4], построим непараметрическую регрессию

n

y (x )=Z у' Мx),              (2)

i = 1

где

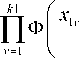
ф

^{e ( x} ) =

n k 1

ЕПф

i = 1 v = 1

ф

В статистике (2) ядерные функции Ф ( и ) удовлетворяют условиям H :

Ф(и) = Ф(-и), 0<Ф(и)<«, |ф(и)du = 1, jи2Ф(и)du = 1, |ит Ф( и) du <ю, 0 < m <« ;

с = c ( n ) , c_v = c_v ( n ) , v = 1, k 1 - коэффициенты размытости ядерных функций, значения которых убывают с ростом объёма n обучающей выборки. Здесь и далее бесконечные пределы интегрирования опускаются.

При оценивании зависимости в ситуациях x = ( x 1 , x ) сначала вычисляется у 1 = F ( x i , a ) , а затем по данным ( x ₍, у 1 ) в соответствии со статистикой (2) определяется значение у ( x ) .

Оптимизация модифицированной непараметрической регрессии (2) по коэффициентам размытости ядерных функций с, cv, v = 1, k 1 осуществляется в режиме «скользящего экзамена» из условия минимума статистической оценки среднеквадратической ошибки аппроксимации искомой зависимости.

Асимптотические свойства непараметрической регрессии. Без существенной потери общности будем считать, что в частичном наборе признаков x _{1 v} , v = 1, k 1 их количество k 1 = 1. В качестве ядерной функции примем функцию вида

. . f^{1 V} U I <  1

Ф( и ) = Ь ^{1 1}

1 n  -   -   ( Y - Y i I

^M ( z 2 ( ^x ) ) = ( ⁿ c 1 c ) EJ ... J ^Ф| — I^х

- = 1 V c ₁ )

f 42

х Ф ^а.

V

Так как

x ,„ - x i

c

p ( x - , x - _v , v = 1, k 2 ) dx i dx'_{X v} ... dx^-_k 2 .

x i , x - , v = 1, k 2 являются значениями од-

них и тех же случайных величин t , t v , v = 1, k 2 с плотностью вероятности p ( t , t v , v = 1, k 2 ) , то

^M ( z 2 ( ^x ) ) = ( c 1 c )   J ... J ^Ф| x ¹— t I ^X

V   ^c 1   )

В этом случае непараметрическая регрессия (2) запишется как

k 2

хФ^ x

V v = 1 c

t , t v , v = 1, k 2 ) dtdt₁...dt_{k 2}.

nii

E у - ф| ^x 1 ^x 1 1 ф| ^y 1 ^y 1

⁼ ( A - = 1       V c 1 ) V c

У ^{( x} ) = ^—7---- - А Г

У _Ф| ^xr - x iL UI 21z2l

^E I c JI c

Проведём замену

.

uv

. ^a v ( ^x 1 v ^- t v )

.

После

(x1 - t) переменных и = ------ , c1

Тогда справедливо следующее утверждение.

Теорема. Пусть 1) частичные сведения y = F (у а ) восстанавливаемой зависимости (1) принадлежат к классу линейных полиномов; 2) функция y = ф ( x ) и плотности вероятностей p ( x ) , p ( x , y₁ ) ограничены вместе со своими производными до второго порядка включительно; 3) ядерные функции Ф ( и ) являются положительными, симметричными и нормированными; 4) последовательности коэффициентов размытости c ₁ ( n ) , c ( n ) ядерных функций таковы, что при n ^ да их значения стремятся к нулю. Тогда непараметрическая регрессия (3) обладает свойством асимптотической несмещённости.

Доказательство. Представим модель (3) в виде

c получим

k 2 - 1

^M ( z 2^{( x} ) ) = I2---

П « v v = 1

в

несложных преобразований

f k 2     A

J ... J ^ф ( u ) ^ф| E u v I^х

V v = 1     )

i                                c                           1

х p | x ₁ - c ₁ и , x _{1 v}--u_v , v = 1, k 2 | dudu₁... du_{k 2}.

V              a v            )

Разложим функцию

p \ ^x 1

c ₁ u , x _{1 v}

——Uv , v = 1, k 1 a v

ряд Тейлора в точке x = ( x ₁, x _{1 v} , v = 1, k 2 ) и преобра-

зуем (6) с учётом свойств:

/    A-1      f x( x - x i A f y - y i A

( nC 1 c ) E y Ф| ---- |ф| ■ ' - ' I _

⁼ ( A               - = 1       V ^c 1 ) V c )     ^z 1 ( ^x )

у ( ^x ) =------------ 7----- Га— =T V =       . ⁽⁴⁾

/     A- 1 V"¹ Л I x - x, I I y - y I z ( ^x )

(nc,c) > Ф  ---^L Ф ———       ⁷

i = 1 V ^c 1    ) V c )

1 1 f k 2     A

J ... J ф| E u v I du₁...du_k 2 = 1,

- 1 -:

1     V v = 1

Проведем преобразования

= M

z 1 ( ^x )

zx

M ^Ц= z 2 ( ^x )

z 1 ( x )

Mz 2 ( x ) z 2 ( x ) Mz 2 ( x )

₁ (5) ( Mz 2 ( x ) - z 2 ( x ) ) ,

где M – знак математического ожидания.

1 11     f 42. A

₂k ; J ... J u t ^Ф| E ^uv I ^d u 1 ... ^duk 2 = 0, t = ^{1 k 2},

²      - 1 - 1       V v = 1 )

1 1 1       f 42. A

₂.- J ... J u t ^ф| E u v I ^du 1 ... du k 2 =P .

²      - 1 - 1        V v = 1 )

В результате при n ^ да имеем k2-1 k2-1

M (z2 (x)) ~ —2

Па v v=1

/•>2                   Z-.2R2 El 1, , х p(x)+уpx)(x)+J-E-ypv)(x)+0(c), 2             2 v=1 a v_

z ( x )

Ввиду ограниченности значений y ( x ) = —--- z 2( x )

свойства статистики (3) зависят от асимптотического поведения M ( z ₁( x )), M ( z ₂( x )). Вычислим

где

сти

x 1 ,

p x A¹ ( x ) , p v ²* ( x ) - вторые производные плотно-вероятности p ( x ₁, x _v , v = 1, k 2 ) по переменным x _v , v = 1, k 2 соответственно.

Следуя приведённой технологии вычислений, найдём асимптотическое выражение для периментов сравнивалась эффективность статистики (2) и традиционной непараметрической регрессии n               (           I ( k2              Y1'

M(z1 (x)) = (ncc) ij.j Уф|       |ф|£аv i=1             ^ cl JI v=1         c

хp(y1,xi,xiv,v = 1,k2) dy'dx'i dx 11 ... dx1 k2 = ck 2—1         (         _ c _____I

= —----J... J фl x ₁ — c ₁ и , x 1 v--u_v , v = 1, k 2 |x

П « v     ¹          “ ^{v         J}

^{y ( x ) =}

nk i уПф

1 = 1       v = 1

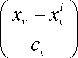
nk iП ф i = 1 v = 1

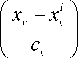
v = 1

( k 2 хф( и ) Ф ^i

I v - т

Ии » | P | x ₁ — c ₁ и , x _{1 v} ——и , v = 1, k 2 | dиdи ₁... dи_{k 2}

В качестве искомой зависимости (1) использовался полином второй степени

ф ( x ) = x 2 + 2 x 2 + x ₁ x ₂ + x 3 + 0,5 x 4 + 2 x ₅,    (12)

~

2 ^{k 2 — 1} c^{k 2 — 1}

k 2

Па v v=1

^а v            )

ф⁽ x ) p ( x ^{) +}-2- ( ф⁽ x ) p ( x ) ) x ^+

2R2 Ji2

i ~ ( ф ( x ) P ( x ))_x^{+ 0} ( c 1 c , c 1 c v , v = ^{1 k 2} ) . ⁽⁸⁾

2 v = 1 a v                  ^{1 v}                                   _

каждый аргумент которого принимает значения из интервала xv e [0;1], v = 1,5 с равномерным законом распределения. Частичные сведения о восстанавливаемой зависимости в соответствии с условиями теоремы определяются линейным полиномом y1 = x3 + 0,5 x4 + 2 x5.

В выражении (8) ( ф ( x ) p ( x ))^'¹ , ( ф ( x ) p ( x ))^'^> -вторые производные произведения двух функций по переменным x ₁, x_tv , v = 1, k 2 соответственно.

Подставим выражения (7) и (8) в (5), получим

, Л z 1 ( x )

M (y (x)) ~ M ■ x ’ Z 2 ( x )

ф( x) p(x)+у (ф( x) p(x)) xx+ c2p2 42 1 / / \ i 2)

+i у(ф( x)p (x)) x1 v v=1 a v

Г              „2r2 k 2 1            "

p ( x ⁾⁺у p x 2 ⁾⁽ x ⁾⁺ i у p v ²⁾⁽ x )

^{2             2}     v = 1 ^a v

Из анализа выражения (9) следует, что при c ₁ = c ₁ ( n ) ^ 0, c = c ( n ) ^ 0 с ростом n ^да изучаемая статистика (3) обладает свойством асимптотической несмещённости.

Замечания. При k 2 = 2 полученные результаты могут быть использованы при исследовании свойств статистических моделей, основанных на методе группового учёта аргументов [5]. Идея метода заключается в построении последовательности моделей

У, =ф j ^{( x} j , У, — 1 ), ¹ = ¹, m .            ⁽¹⁰⁾

Ранее не используемая в моделях y_z , t = 1, j — 1 компонента x_j вектора аргументов x обеспечивает в наборе с у — _{— 1} минимальное расхождение значений y _j с экспериментальными данными. На каждом этапе процедуры (10) искомая зависимость оценивается в пространстве двух переменных ( x j , y j _{— 1}).

Анализ результатов вычислительных экспериментов. На основании данных вычислительных экс-

При формировании обучающей выборки

V = ( x^l_v , v = 1,5, y¹ , 1 = 1, n ) на значения функции (12)

накладывалась аддитивная помеха y1 =V(V)(1 + 2 (s1— 0,5) r), (13)

где s - случайная величина с равномерным законом в диапазоне [ 0; 1 ] ; r - параметр, определяющий уровень шума.

При синтезе непараметрических моделей (2), (11) использовалась ядерная функция Епанечникова, а их оптимизация по коэффициентам размытости осуществлялась в режиме «скользящего экзамена» из условия минимума среднеквадратического критерия. При этом полагалось, что значения коэффициентов размытости c_v = c , v = 1,5 для непараметрической регрессии и c_v = c , v = 1,2 - для модели (2), так как интервалы изменения аргументов восстанавливаемой зависимости априори одинаковые. В качестве критерия эффективности моделей (2), (11) принимались среднеквадратические отклонения W ₂ , W ₁₁ их значений от функции (12), которые оценивались по контрольной выборке V_k объёма n_k = 10 000. При этом ситуации из выборки V_k , в которых исследуемые непараметрические модели не идентифицируют значения функции (12), не участвуют в формировании критериев их эффективности. Доля таких ситуаций не превышает значений 0,06 от объёма контрольной выборки.

Вычислительные эксперименты при фиксированных условиях исследования осуществлялись 60 раз. По полученным результатам восстанавливались плотности вероятности p ( W 2 ), p ( W₁₁ ) оценок среднеквадратических отклонений W ₂ , W ₁₁ соответственно моделей (2), (11) (см. рисунок).

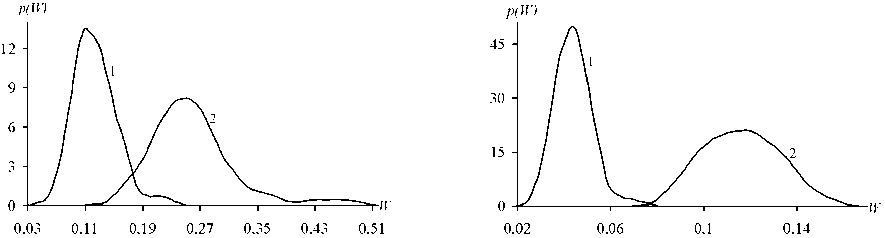
Оценки плотностей вероятностей p ( W 2 ) , p ( W 1 ) среднеквадратических отклонений модифицированной непараметрической модели у (кривая 1) и непараметрической регрессии у (кривая 2). Условия эксперимента: объём обучающей выборки n = 50 ( а ), n = 200 ( б ); уровень шума в процедуре (13) r = 0,1

Анализ данных вычислительных экспериментов показывает, что статистические оценки законов распределения значений критериев эффективности W ₂ , W ₁₁ достоверно отличаются при различных объёмах обучающих выборок, причём интервалы изменения среднеквадратического критерия W ₁₁ непараметрической регрессии (11) характеризуются большими их значениями по сравнению с модифицированной регрессией (2). С ростом объёма обучающей выборки преимущество моделей (2) возрастает. Например, отношение R = W 11 (W^ средних значений W ₂, W 11 соответствует 2, 3 при n = 50 и 3 при n = 200.

Эффективность модифицированной непараметрической модели (2) объясняется возможностью снижения её размерности за счёт использования априорных сведений о наличии линейной взаимосвязи между переменными исследуемой зависимости. Данное заключение согласуется с результатами исследования гибридных моделей стохастических зависимостей [1].

Традиционная непараметрическая регрессия, основанная на оценке плотности вероятности типа Ро-зенблатта–Парзена, обобщена при построении статистических моделей в условиях наличия частичных сведений о виде восстанавливаемых зависимостей. Предлагаемая модифицированная непараметрическая регрессия обладает свойством асимптотической несмещённости. Это позволяет аналитически обосновать возможность частичного сжатия пространства признаков на основе линейных преобразований без существенной потери полезной информации.

Перспективное направление дальнейших исследований состоит в развитии предлагаемого подхода на анализ свойств статистических моделей, основанных на методе группового учёта аргументов.