Непараметрические алгоритмы идентификации и управления для Т-процессов

В настоящее время задачи идентификации и управления многомерными дискретнонепрерывными системами с запаздыванием в условиях априорной неопределенности являются достаточно важными [1]. Во многих производствах добычи, переработки и хранения продукции обычно технологи имеют дело с многомерными дискретно-непрерывными процессами. Например, при производстве конвертерной стали происходят сложные физико-химические реакции и поэтому отсутствие адекватной модели может привести к неудачному управлению конвертером, связанному с большим отличием (более 5 %) значений выходных переменных от заданных. В таком случае построение параметрической модели конвертерного производства приведет к проведению большего числа экспериментов и соответственно к многочисленным затратам, в то время как использование непараметрических моделей существенно сокращает затраты и позволяет уменьшить время на создание адекватной модели [2].

Подобные многомерные объекты (процессы) имеют чаще всего зависимости выходных переменных x = (x1,x2,...,xn), стохастически зависимых заранее неизвестным образом (Т-процессы). Это приводит к тому, что математическое описание многомерного объекта будет представлять- ся в виде некоторого аналога системы неявных функций вида Fj (u, x) = 0, j = 1, n , где u = (u1,u2,...,um ) - входные переменные процесса. Основная особенность подобных объектов состоит в том, что класс зависимостей F (•) неизвестен с точностью до параметров. В этом случае классическая теория идентификации не применима. Задача идентификации сводится к задаче решения системы нелинейных уравнений Fj- (u, x) = 0, j = 1, n относительно компонент вектора x = (x1,x2,...,xn) при известных значениях u, x и наличии обучающей выборки (ui, xi, i = 1, s), которая может быть решена при использовании теории непараметрических систем [1]. Подобные задачи ранее не рассматривались [3; 4].

Воспользуемся конкретизацией понятия, связанного с термином «непараметрический», которое было использовано в работах М. Розенблатта и Э. Парзена [5; 6], а также в монографии Ф. П. Тарасенко [7].

«Непараметрическая задача – это статистическая задача, определенная на таких классах распределений, среди которых хотя бы один не сводится к параметрическому семейству функций».

«Непараметрическая задача оценивания неизвестных распределений – это задача нахождения процедуры, с помощью которой можно оценивать непараметризованные распределения из класса, например, всех непрерывных функций распределения или класса распределений, имеющих ряд производных и т. д.».

В настоящей же статье термин «непараметрический» означает отсутствие достаточной априорной информации для представления объекта с точность до параметров.

Исходя из данных определений, можно сказать, что непараметрические методы намного выигрывают в эффективности, если параметрическая модель не описывает адекватно наблюдаемые данные [8].

Задача идентификации

Рассмотрим многомерный процесс, представленный на рис. 1.

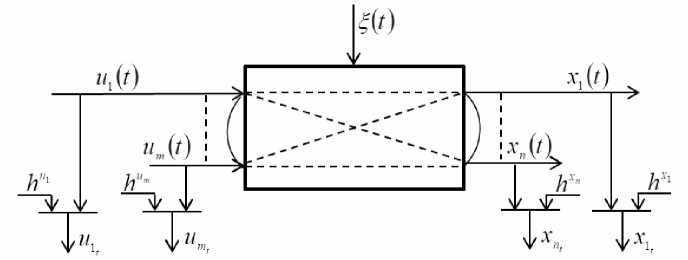
Рис. 1. Многомерный объект

Fig. 1. Multidimensional object

На рис. 1 приведены следующие обозначения: u(t) = (u1 (t),u2 (t),...,uk (t),...,um (t)), k = 1,m - m-мерный вектор входных переменных; x(t) = (x1 (t),x2 (t),...,xj (t),...,xn (t)), j = 1,n - n-мерный вектор выходных переменных, которые принадлежат соответствующим областям: xj eQ j (x); ^(t) - случайные помехи, действующие на объект; hu, hx - случайные помехи измерений соответствующих переменных процесса; пунктирные линии свидетельствуют о наличии зависимости входных и выходных переменных; (t) – непрерывное время; ut,xt – измерения входных и выходных переменных в дискретный момент времени t.

На основании вышеизложенного можно сказать, что многомерные процессы окружают нашу повседневную жизнь и представляют собой процессы, имеющие много входов и выходов, а также связи входных и выходных переменных между собой, связи только между входными переменными [9; 10] и только между выходными. Причем все эти связи не всегда известны исследователю [11], а может также присутствовать разнотипная априорная информация [12]. В вязи с тем, что выходные переменные многомерного процесса связаны между собой, следует отметить и составной (ситуационный) вектор, который был введен Я. З. Цыпкиным в [13]. Составной вектор – это вектор, составленный из входных и выходных переменных. Это может быть любой набор, например x < 3 > = ( и 2 , и 5 , ц 1 , x 4 ) . Составной вектор известен исследователю из априорной информации.

Рассмотрим понятие запаздывания в многомерном объекте. В одном случае запаздывание – это природное свойство объекта (например, это может быть длительность процесса измельчения клинкера для получения цемента). В другом случае, задержка будет связана с дискретностью измерений, например, если выходные характеристики процесса или объекта можно наблюдать только через некоторый период времени. Таким образом, в теории управления запаздывание и задержку следует различать по-разному. Следует учитывать, что задержка может зависеть от аппаратуры и технологии измерения, когда измерения выходных переменных осуществляются в различные промежутки времени, например раз в два часа, раз в смену, раз в сутки и т. д.

Задача идентификации многомерных объектов заключается в построении моделей этих объектов, которые условно можно представить на рис. 2.

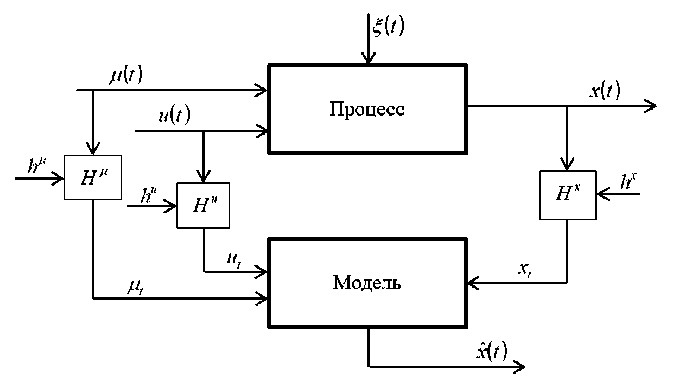
Рис. 2. Многомерный дискретно-непрерывный процесс

Fig. 2. Multidimensional discrete-continuous process

На рис. 2 на вход рассматриваемого процесса поступает вектор входных управляемых переменных и(t) = (и1 (t),...um (t)) e (и) c Rm и вектор входных неуправляемых, но контролируемых переменных ц(t) = (ц1 (t),...Цp (t))е(ц)с Rp, на выходе наблюдается вектор выходных переменных x(t) = (x1 (t),...xn (t)) e(x) c Rn, x(t) - выход модели. Входные и выходные перемен- ные контролируются в дискретные моменты времени через интервал At. Средствами контроля Hu, HЦ, Hx получаем выборку наблюдений или обучающую выборку. В каналах измерения переменных действуют случайные помехи hu, h Ц, hx.

Как было сказано выше, процессы, рассматриваемые в настоящей работе, имеют неизвестные зависимости компонент выходных переменных. Поэтому исследуемый процесс будет описываться системой неявных стохастических уравнений:

F j ( u ( t ) , ц ( t ) , x ( t + т ) , ( t ) ) = 0, j — 1, n ,

где функции F j ( ■ ) не известны, так как не известны зависимости выходных переменных; т - известное запаздыванием по различным каналам изучаемого процесса.

Задача идентификации состоит в построении модели системы, которая представлена на рис. 2, при наличии выборки наблюдений над объектом: u i — ( u i 1 , u i ₂, ..., u im ) , ^Ц i ^{— ( ц} i i , ^Ц i 2 , ..., ^Ц ip ) , ^x i — ^{( x} i 1 , ^x i 2 , ..., ^x i _n ) , i ^— 1, s .

В этом случае Т-модель процесса с неизвестными зависимостями компонент вектора выходных переменных будет рассматриваться в виде системы:

F j ( u < j > , Ц < j > , x < j > , u s , Ц s , x s ) — 0, j — 1, n ,

где u < ^j > , ц < ^j > , x < ^j > - составные векторы, u_s , Ц _s , x_s - временные векторы (т. е. набор данных, которые поступили к s -му моменту времени).

В результате измерения входных и выходных переменных может быть получена обучающая выборка ui —(ui1, ui2, ..., um), Цi — (цп, Цi2, ..., цip), xi —(xn, x^, ..., xn), i — 1,s, которая используется при построении модели многомерного объекта. Так как входные воздействия u заданы и известны, то решаем систему (2) и получаем оценки xj компонент вектора выходных переменных xj при соответствующих значениях входных воздействий u . Здесь естественно воспользуемся методами непараметрического оценивания [14].

Для начала подставляем l -е поступление входных переменных u_l — ( u_l 1 , ..., u_lm ) , l — 1, s , где s - объем обучающей выборки, в формулу (2). Далее подставляем выходные переменные из обучающей выборки x i — ( x i 1 , ..., x_in ) для определения невязок е i , i — 1, s . Невязки e i , i — 1, s вычисляются по следующей формуле:

e j — f j ( u < j > , Ц < j > , x < j > , u _s , Ц s , x s ) , j — 1, n ,

где функции f j ( ■ ) принимаются в виде разницы между измеренными значениями компонент выхода и их оценками [15]:

^е j

⁽ i ^{) — x} j ⁽ i ^{) -}

s       <  m >             r-iA< Р >

X j i 1 П Ф ^u f i¹ П Ф " ^Ц i ¹

i — 1        k — 1    у    c su k    J v— 1    у     c s ц_{у    2}

^s < ^m >                   Р >

хпФ uk-^^ пФ

i — 1 k — 1 у c su k J v— 1 у

Ц^-Цу[ i1Л — cs Цу    J

j — 1, n ,

где <  m >  - размерность составного вектора u_k , <  m ><  m . Далее оцениваем условное математическое ожидание

X j = M { X j I u < j > , Ц < j > , ^e = 0 } , j = 1, n ,

и в конечном итоге прогноз для каждой компоненты вектора выходных переменных будет выглядеть следующим образом:

^

x j =

x        <  m >              Г11А< p >                     n >

2 х , и - П Ф   ¹   u^{k 1} [ i ¹ П Ф "' '   i ¹ П Ф ^

i = 1         k 1 = 1    V      c su     J v i = 1    V      c s ц       J k 2 = 1    V   c s e   J

t П■ Ф [ u        11^ ^

i = 1 k 1 = 1 V c su J V 1 = 1 V

^{Ц v 1} ^i ¹ ^ П Ф ^e i ¹ '

c s ц      J k 2 = 1 V c s e J

j = 1, n,

где в качестве колоколообразных функций Ф ( - ) были приняты функции различных типов и коэффициенты c_su , c_{s ц} , c_{s e} удовлетворяли условиям сходимости [16].

Оценка (6) и является прогнозом выходных переменных x при известных входных u .

Задача управления

Рассмотрим многомерный объект – блок-схему с запаздыванием, общая схема управления которого представлена на рис. 3.

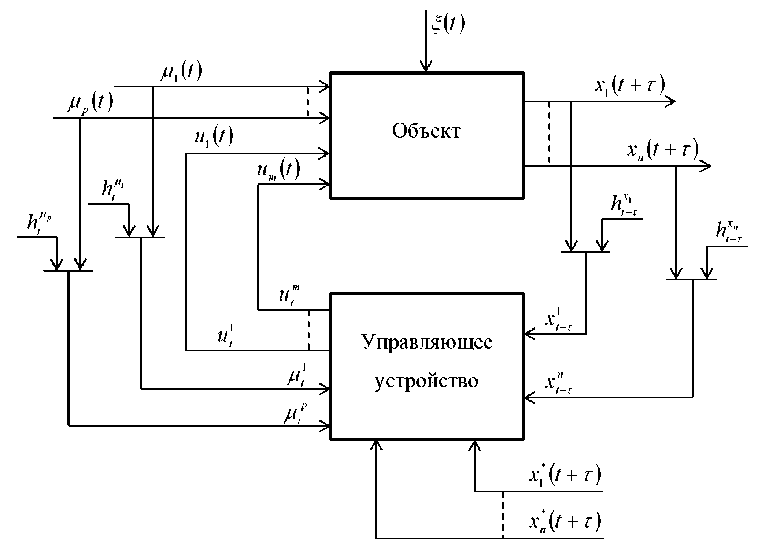
Рис. 3. Схема непараметрической системы управления объектом с запаздыванием

Fig. 3. Scheme of a nonparametric control system for an object with delay

На рис. 3 приняты следующие обозначения: u(t) = (u1 (t), ..., um (t)) - управляемые входные переменные; ц(t) = (ц1 (t), ..., цp (t)) - неуправляемые, но контролируемые входные перемен ные; x(t + т) = (x1 (t + т), ..., xn(t + т))еRn - выходные переменные процесса; x*(t + т) = (x*(t + т), ..., xn*(t + т))еRn - задающие воздействия; ^t, ЬЦ, hX - случайные стационарные помехи, действующие на объект и в каналах измерения входных и выходных пере- менных; т - запаздывание по различным каналам многомерной системы. Запаздывание т известно по всем каналам многомерной системы, и в данном случае является одинаковым для каждой компоненты вектора выходных переменных.

Если принимать во внимание, что выходные переменные многомерного Т-процесса стохастически связаны между собой, то определение задающих воздействий для такой системы приобретает некоторое отличие. Так как выходные переменные связаны, то общее пересечение они имеют в некоторой области Q j (Xj), но не всегда все выходные переменные будут пересекаться в одной области. В том случае если эта область Q j (xj) существует, то задающие воздейст- вия необходимо выбирать только из этой области, в противном случае управление такой системой не представляется возможным. В случае если такой области нет, то управлять такой системой бесполезно. При этом приведем систему управления многомерным объектом, в которой рассмотрим систему взаимосвязанных задающих воздействий (рис. 4).

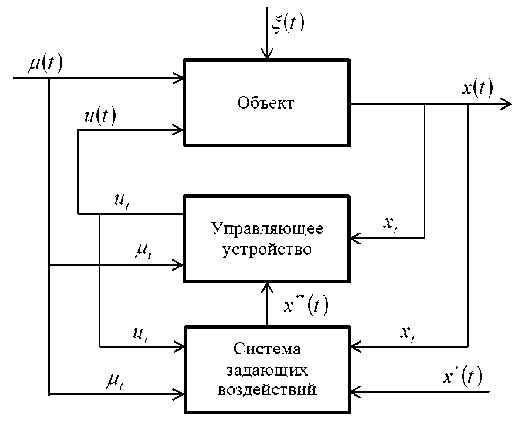
Рис. 4. Схема непараметрической системы управления с дополнительным блоком

Fig. 4. Diagram of a nonparametric control system with an additional block

Рис. 4 в отличие от рис. 3 дополнен блоком формирования задающих воздействий для их определения. На рис. 4 приняты следующие обозначения: x * ( t ) - исходные значения задающих воздействий; x ** ( t ) - задающие воздействия, которые необходимо найти из системы уравнений

Fj(u(t), p(t), x*(t)) = 0, j = ^i, (7) где функции Fj (•) продолжают оставаться неизвестными. Изложим процедуру управления, начиная с конкретного момента времени t.

Пусть имеется обучающая выборка (ul, pi, xi, i = 1,s). В конкретный момент времени t на вход поступают неуправляемые, но контролируемые переменные pt, при этом управляющие воздействия ut и выходные переменные xt пока неизвестны. Далее из всей первоначальной выборки (ui, pi, xi, i = 1, s) выбираются те строки, в которых значения pi наиболее близки к вновь поступившим значениям pt, и из этих строк формируется новая выборка. Задающие воздействия x * * находятся из новой сформированной выборки x ** е A (Xj), а именно из решения системы (7). Решение системы (7) сводится к последовательности алгоритмов, изложенной ниже.

Для задающего воздействия X * берем произвольные значения из области Q , ( X 1 ) . Вторую переменную х 2 * определяем с учетом выбранной компоненты x* из следующего выражения:

X *”

s ₁

Е х 2 Ф i=1

i

X 1 - X 1

< m >

П Ф к=1

i uk uk

V cuk

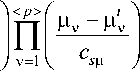
s ₁

Е ф i =1

i

X 1 - X 1

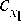
< m >

П Ф к=1

u k ^- u k

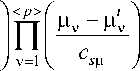
где $ 1 cfi ( X 1 ) , т. е. суммирование проводится не по всей первоначальной выборке, а только по тем значениям, которые были наиболее близки к вновь поступившим значениям ц _t.

В общем виде алгоритм принимает следующий вид:

** $ x_j

$ j - i     j - 1

Е X i П i = 1 j = 1

x

x

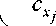
< m >

П Ф k=1

i uk- uk

V c u k

A< p>(        i

П

J v= 1 V     c ц

$ j - 1 j - 1

ЕП

** i

Xj - Xj cxj

< m >

П Ф

J k = 1

i uk- uk

V cuk

A <  p > ( i

П '

J v= 1 V c $ ц

После определения задающих воздействий можно приступать к нахождению прогнозных значений управляющих воздействий для многомерной системы. Для этого воспользуемся следующим непараметрическим алгоритмом. Входную переменную и 1 ( t ) берем произвольно из области Q ( и 1 ) . Входная переменная u ₂ ( t ) может быть определена в соответствии со следующим алгоритмом:

^и 2 =

s

Е и 2 ф

V

u 1 ^{- u} 1 ^ П ф c U 1 J j =1

i

Ц у ^- ц V

s

Е Ф i=1

^u 1 ^{- u 1} J fr Ф c U 1 J j =1

x

**

x i_j

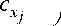
p

П ^Ф

V=1

Цу -ц V ^

V ^C Ц v J

где ( u i , ц i , X i , i = 1, $ ) - обучающая выборка; ц _у - поступившие входные неуправляемые, но контролируемые переменные.

Для входной переменной и 3 ( t ) алгоритм управления будет выглядеть следующим образом:

и з —

si

U] - U]

и³Ф      ¹

i = 1        V c u 1

i

Ф u iz u !

c u ₂

ПФ

^J j = 1 V

i цу -цv

^С ц у    j

s

Е ф i=1

i

U 1 - U 1

Ф

u ₂

-

i ^ u 2

V

c u ₁

V

c u ₂

J

П [ r“ _ Y i ) P

П Ф ^XjT^JX1- П Ф j = 1 V c^X j J ^v = 1 V

i ц у -ц v

^С ц у    j

и так далее для каждой компоненты входа и ( t ) объекта. В общем виде для многомерной системы алгоритм управления будет выглядеть следующим образом:

s

k - 1

Z uk П Ф

uk uk

x

^^^^^^^B

x

k

s

i = 1

k = 1

c_{u k}

c

: • p

j ПФ

v= 1

k v

к

^^^^^^^B

i ^ k v

c

k v

x k - 1

uk uk

x

••

^^^^^^^B

x

i = 1 k = 1

c u_k

c

: . p г П Ф

v= 1

k v

^^^^^^^B

i

Ц у

k = 1, m .

к

c

k v

В реальных задачах часто число компонент вектора входных переменных u больше числа компонент вектора выходных переменных x . В этом случае в число компонент вектора ц включают компоненты вектора u ,, с тем, чтобы размерность вектора u и x сделать одинаковой.

Настраиваемыми параметрами будут параметры размытости cu , cx и с , для них можно k j * v использовать следующие формулы: cuk =а |uk - u*k |, cxj = в| x * * - xj| и c*v = y|*v -Ц v |, где а, в и y некоторые параметры большие 1, а > 1, в > 1, y > 1. Следует заметить, что выбор c , cx. и kj с осуществляется на каждом такте управления. При этом если сначала определен cu , то оп-kv                                                                                                                      k ределение cxj и сkv осуществляется с учетом этого факта. Однако может быть и наоборот, например, сначала определяется cxj. или сkv, а потом остальные.

Вычислительные эксперименты

Для примера был взят объект с 4-мя входными переменными u ( t ) = ( u 1 ( t ) , u 2 ( t ) , u 3 ( t ) , u 4 ( t ) ) и тремя выходными переменными x ( t ) = ( x 1 ( t ) , x 2 ( t ) , x 3 ( t ) ) . Подобные объекты характерны для реальных производств, например, для производства цемента, нефтепереработки, металлургии и т. д., где протекают только многомерные процессы. Для данного объекта была сформирована выборка входных и выходных переменных и найдены прогнозируемые значения выходных переменных при известных входных с использованием алгоритма (4) и (6). Для вычисления использовался объем выборки s = 1000, параметры размытости c_su = 0,4; c_{s £} = 0,2, помеха, действующая на компоненты вектора выходных переменных а = 0,1 , запаздывание т = 2 такта (где 1 такт равен 1 минуте либо иной). Описание объекта с точностью до параметров было принято только для проведения компьютерного исследования и оставалось неизвестным для изложенной выше теории. Представим полученные результаты для третьей компоненты выхода многомерного объекта.

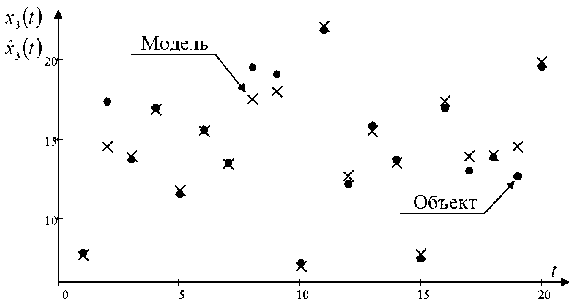
Рис. 5. Прогноз выходной переменой x 3 ( t ) объекта, измеренный с равномерной помехой 10 %, 5 3 = 0,07

Fig. 5. The predicted output variable x 3 ( t ) of the object, measured with a uniform noise of 10 %, 5 ₃ = 0,07

На рис. 5 представлены полученные прогнозируемые значения x ₃ ( t ) для третьей компоненты выхода x 3 ( t ) . Погрешности определения переменных обусловлены наличием помех. Как видно из рис. 5, прогноз значений выходных переменных x ₃ ( t ) многомерного объекта по известным входным переменным u ( t ) с учетом 10 % помехи достаточно удовлетворителен с точки зрения многих задач практики (например, процесс измельчения клинкера). Обратим еще раз внимание на то, что исследователю неизвестен вид системы уравнений, описывающий управляемый объект. В качестве информации о последнем используются измерения входных и выходных переменных ( и¹ , ц i , x i , i = 1, s ) .

Далее приводятся результаты вычислительных экспериментов для данного объекта для первой компоненты выхода при использовании алгоритма управления (12). В данном вычислительном эксперименте число компонент вектора u больше числа компонент вектора х . Если же размерность вектора u превышает размерность вектора х , т. е. m >  n , то сделаем замену: и 4 ( t ) ^Ц 1 ( t ) , чтобы размерность вектора и и x сделать одинаковой. Далее значения задающих воздействий x** ( t ) , которые были найдены при помощи алгоритма (9), представим в виде ступенчатой функции, как показано на рис. 6.

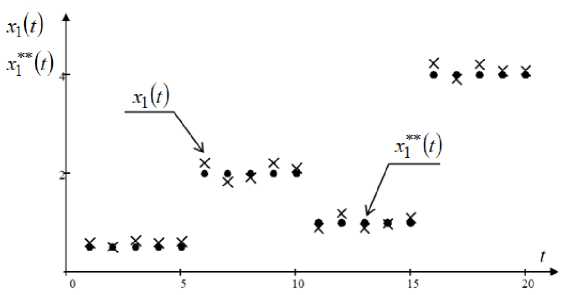
Рис. 6. Зависимость выхода объекта x 1 ( t ) от задающего воздействия x ** ( t )

Fig. 6. Dependence of the output of the object x 1 ( t ) on the setting action x ** ( t )

Как видно из рис. 6, выход объекта x 1 ( t ) достаточно близок к задающему воздействию x ** ( t ) при наличии 10 % помехи и не превышает 1,7 % от значений x ** ( t ) , что удовлетворяет большинству практических задач.

Таким образом, непараметрический алгоритм управления многомерным объектом со стохастически зависимыми выходными переменными x ( t ) показывает достаточно точные результаты с точки зрения многих практических задач.

Заключение

В настоящей статье рассматриваются задачи идентификации и управления многомерным объектом в условиях неполной информации об объекте исследования, т. е. в условиях, когда параметрическая модель процесса не определена. Такие многомерные объекты часто встречаются на практике, например в металлургии, энергетике, нефтепереработки и в других отраслях. Отличительная особенность моделей этих объектов и алгоритмов от известных состоит в том, что задачи ставятся в условиях непараметрической неопределенности, т. е. в условиях, когда многомерная система не описывается с точностью до вектора параметров из-за недостатка априорных данных.

Еще основной особенностью является то, что и при задаче идентификации и задаче управления вводятся последовательности непараметрических алгоритмов. Сущность непараметрических алгоритмов идентификации и управления состоит в том, что для задачи идентификации прогноз выстраивается как условное математическое ожидание компонент вектора выходных переменных x ( t ) при известных компонентах входных u ( t ) , а при управлении - как условное математическое ожидание входных переменных u ( t ) при найденных задающих воздействиях x "(t ) .

Исходя из полученных прогнозируемых значений в вычислительном эксперименте, в процессе использования непараметрических алгоритмов, получаются достаточно хорошие с практической точки зрения результаты, которые можно использовать и при решении реальных задач на производствах [17].