Непараметрические многошаговые алгоритмы моделирования и управления многомерными безынерционными системами

Введение. Рассмотрение и изучение многомерных безынерционных процессов с запаздыванием, имеющих стохастическую зависимость выходных переменных, является сравнительно актуальной задачей, так как подобные процессы характерны для многих востребованных отраслей промышленности, например, в металлургии (плавка стали), стройиндустрии (производство цемента), энергетике (горение угля), нефтепереработке (повышение хладотекучести дизельного топлива) [1], а также в активных системах, таких как образовательный процесс (приобретение знаний студентами университетов) [2]. Для данных процессов характерным является отсутствие необходимой априорной информации. Исследователю, находящемуся в таких условиях, необходимо моделировать и управлять подобными многомерными дискретно-непрерывными процессами. Эти процессы динамические по своей природе, но контролируемые через дискретные интервалы времени, в том числе различные. Безынерционные системы рассматриваются с известными запаздываниями, например, когда постоянная времени объекта составляет 5–10 мин., а контроль выходной переменной измеряется раз в два часа. Это приводит к зависимости выходных переменных, например, при производстве цемента основной показатель на выходе - активность цемента (прочность при сжатии) зависит от другого показателя выхода -тонкости помола.

Процессы, у которых наблюдалась стохастическая зависимость выходных переменных, были отнесены к Т-процессам [3]. Главное здесь состоит в том, что идентификация подобных объектов должна осуществляться не традиционным для существующей теории идентификации путем [4]. Здесь также возникают случаи, когда априорная информация соответствует одновременно как непараметрическому, так и параметрическому типу исходных данных об исследуемом процессе. Такие процессы были отнесены к КТ-процессам [3].

Главной особенностью Т-процессов и КТ-процессов является то, что математическое описание объекта представляется в виде некоторого аналога системы с частично параметризованными функциями F .( u , x , а ) = 0, j = 1, n и неизвестными функциями вида Fj ( u , x ) = 0, j = 1, n . Таким образом, задача идентификации сводится к задаче решения системы нелинейных уравнений частично-параметризованного дискретно-непрерывного процесса относительно компонент вектора x = ( x_x , x ₂,..., x_n ) при известных значениях входных переменных u = ( u_x , u ₂,..., u_m ) . Конкретные задачи идентификации будут отличаться различными объемами априорной информации по различным каналам многомерного процесса, особенностью их протекания. Здесь стоит отметить, что приходится сталкиваться с системой разнотипных, с точки зрения математики, уравнений, решение которых будет требовать развития специальных методов [5]. В этом случае целесообразно использовать теорию непараметрических систем [6; 7].

Процессы, имеющие стохастическую зависимость выходных переменных. Как было отмечено ранее, Т-процессы - это многомерные безынерционные процессы, имеющие стохастическую зависимость выходных переменных. Рассмотрим на рис. 1 исследуемую многомерную систему, реализующую Т-процесс.

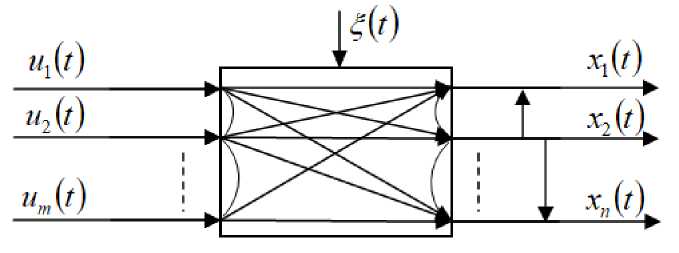
Рис. 1. Многомерная система, реализующая Т-процесс

Fig. 1. The multidimensional system that implements the T-process

На рис. 1 приняты следующие обозначения: u = ( u_x ,..., и_т ) - m -мерный вектор входных переменных, x = ( x ,,..., x_n ) - n -мерный вектор выходных переменных, ^ ( t ) - случайные помехи, действующие на процесс. Вертикальные стрелки на выходных переменных показывают их зависимости. По различным каналам многомерного процесса зависимость j -ой компоненты вектора x может быть представлена в виде некоторой зависимости от тех или иных компонент вектора u : x < j > = f ( ц .< j > ) j = 1, n . Подобные функции определяет исследователь на основании имеющейся априорной информации. Такие соотношения называются составным вектором. Составной вектор это вектор, составленный из некоторых компонент входных и выходных переменных, в частности, это может быть любой набор, например x < 5 > = ( u ₂, u ₅, u ₇, u₈ ) , x < 6 > = (u₈ , u , u ₇, x^ ) [8].

Математическое описание объе кт а представляется в виде некоторой системы неявных функций вида F j ( u ( t ), x ( t )) = 0, j = 1, n . Задача идентификации сводится к задаче решения системы нелинейных уравнений

F j ( u ( t ), x ( t )) = 0, j = 1, n (1)

относительно компонент вектора x при известных значениях входных переменных u .

Заметим, что вид уравнений F ( • ) , j = 1, n продолжает оставаться неизвестным и не может интерпретироваться как модель исследуемого процесса. Задача состоит в моделировании подобных процессов, т. е. Т-процессов.

Частично-параметризованные многомерные процессы. Частично-параметризованные многомерные КТ-процессы отличаются от Т-процессов тем, что у них по некоторым каналам априорная информация может соответствовать параметрическому типу, а по другим – непараметрическому.

Особенностью идентификации многомерного объекта является то, что исследуемый процесс описывается системой неявных стохастических уравнений вида

F j ( u ( t ) , x ( t + t ), ^ ( t ) ) = 0, j = 1, n , (2)

где по некоторым каналам функции F _y ( • ) - не известны, а по другим каналам известны, t -запаздывание по различным каналам многомерной системы [3]. В дальнейшем, из соображений простоты, т будет опущено путем сдвига значений в матрице наблюдений на величину т .

В этом случае система уравнений примет вид

F (u ^<  j > , x ^<  j >  , a ) = 0,

F ₂ ( u < ^j > , x < ^j > , a ) = 0,     _

« ...                           j = 1, n ,                                       (3)

F n - i ( u j , x ^{< j} > ) = 0,

_ F n ( u < ^j > , x < ^j > ) = 0.

где F₃ ( • ) частично параметризованы либо неизвестны, а - вектор параметров.

Моделирование многомерных безынерционных процессов. Многомерные КТ-модели объединяют в себе Т-модели и К-модели и представляют собой модель, в которой есть совокупность взаимосвязей входных и выходных переменных, причем по одним каналам они известны, например, ориентируясь на известные законы физики, а по другим каналам такие зависимости неизвестны, т. е. наличие априорной информации по различным каналам многомерного объекта соответствует как параметрическому, так и непараметрическому типу исходных данных. Поэтому представим систему моделей в следующем виде:

F_x (u < j > , x < j >  , а ) = 0;

F 2 u ^{<  j} > , x >  , a ) = 0;

«...                               j = 1, n ,

^Fn — I ( u < ^j > , x < ^j > , x s , u s ) = 0;

_ F n ( u < ^j > , x < ^j > , x s , u s ) = 0.

где x_s , u_s - временные векторы (набор данных, поступивший к s-му моменту времени), u ^> , x ^> - составные векторы. Но и в этом случае некоторые функции F ( • ), j = 1, n остаются неизвестными. Поэтому задача построения КТ-моделей рассматривается в условиях непараметрической неопределенности, т. е. в условиях, когда система (4) известна лишь по некоторым каналам и не известна с точностью до параметров по другим.

Задача идентификации сводится к тому, что при заданных значениях вектора входных переменных u необходимо решить систему (4) относительно вектора выходных переменных x . По некоторым каналам многомерной системы, по которым известны уравнения с точностью до параметров, коэффициенты находятся, например, методом стохастических аппроксимаций или методом наименьших квадратов [9; 10]. По остальным каналам, где неизвестны уравнения с точностью до вектора параметров, необходимо применить следующую двушаговую алгоритмическую цепочку [3], которая позволит найти прогнозные значения вектора выходных переменных по известным входным. На первом шаге вычисляются невязки по следующей формуле:

£ _ц = F j ( u <  j > , x <  j >  ( i ) , x s , u s ), j = 1, n ,

где F ( u < ^j > , x < ^j > (i ), :x_s , H_s ) принимаются в виде непараметрической оценки функции регрессии

Надарая - Ватсона [11]:

^£ ,■ ( i ) = F _i j ( ^u <  j > , ^x _J ^{( i} ) ) = ^xj ^{( i )-}

s       <  m >

E x j [fl O ф i = 1          k = 1    ^

u k ^- u k ^[ i ^]

s <  m >  (

ЕПф i=1 k=1    ^

c ^su k      у

^uk ^- u k ^[ i ^] '

c suk     у

где j = 1, n, , < m >  - размерность составного вектора uk, далее это обозначение используется и для других переменных. Причем размерность составного вектора может быть различной для разных каналов. Колоколообразные функции Ф(■) и параметр размытости c удовлетворяют некоторым условиям сходимости и обладают следующими свойствами [12]:

Ф0<<» ;lims ,„ cs = 0; J Ф cu (uk - uk [ i ]%u = 1;(7)

Q ( u )

lims ,, <Ф(c-1t(uk -uk[i]))= 3(uк -uk[i]); lms ,, scs = w .(8)

Второй шаг состоит в оценивании условного математического ожидания:

Xj = M {x | u , £ = o}, j = 1, n .(9)

И в конечном итоге прогноз для каждой компоненты вектора выходной переменной будет находиться следующим образом:

^ x ˆ j

s         <  m >

£ X j [ i ] ■ П Ф i = 1             k 1 = 1

s < m >

£П ф

f ukl

f u,

V

- £ [ i ] ^ < n >   f £ [ i ] )

—— ПФ — csu     / k 2 =1 V cs£  )

i = 1 k_x = 1 V

- u [ i ] ) < n >   f £ [ i ] )

—— П Ф csu      7 k 2 =1 V  cs£  /

j = 1, n

где колоколообразные функции Ф ( ■ ) могут быть взяты в виде треугольного ядра (11) и (12), и удовлетворяют условиям, представленным выше.

f u_k - u_k [ i ] ) ф jkк^_

V      c su      7

Ф

f f k ₁ [ i ] 1

V   c s £  7

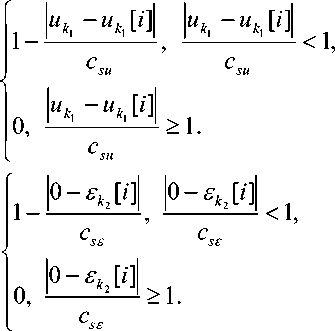
Непараметрический алгоритм (6), (10) представляет собой двушаговую алгоритмическую цепочку, позволяющую находить прогнозные значения компонент вектора выхода при известных компонентах входных переменных, в случае стохастической зависимости выходных переменных.

За функцию ошибки принимается относительное среднеквадратическое отклонение

s

£⁽ x j ⁽ t ^)- x ^{i ( u} < ^j > ( t ) ))

^j = 1, n ,

i = 1 _______________________________________

1L(x‘j(t)-Mx, f i=1

где x i ( t ) - наблюдения на объекте,

Xi,(u ">(t))

прогнозные значения выходных переменных

объекта, M – среднее значение по каждой компоненте вектора x .

Задача управления многомерными дискретно-непрерывными процессами.

Рассмотрим схему системы управления многомерным объектом (рис. 2).

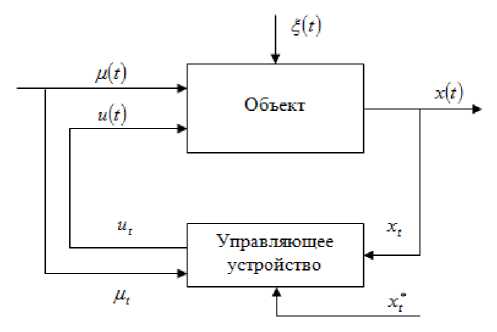
Рис. 2. Схема непараметрической системы управления безынерционным объектом Fig. 2. Diagram of a nonparametric control system of an inertialess object

На рис. 2 введены следующие обозначения: и ( t ) = ( и 1 ( t ) , и ₂ ( t ),

...

управляемые переменные процесса; м ( ^ ) = ( м ( t )’ М ( t X

...

, ^и т ^{( t} ))

–

входные

, m ( t ) ) — входные неуправляемые, но

контролируемые переменные процесса; x ( t ) = ( x 1 ( t ), x ₂ ( t ) ,

...

, x n ( t )) - выходные переменные

процесса; x = ( x 1

,...,

x j ) e^ ( x ^j) c R ⁿ - задающее воздействие, ^ ( t ) - случайные помехи,

действующие на объект [13].

Управление Т-объектами рассматривается в условиях непараметрической неопределенности, т. е. в условиях, когда модель процесса с точностью до вектора параметров отсутствует полностью. В этом случае известные приемы не применимы и следует использовать другие подходы для решения задачи.

В задаче управления многомерным процессом со стохастической зависимостью выходных переменных необходимо использовать следующую многошаговую алгоритмическую цепочку: входную переменную и_х * ( t ) берем произвольно из области Q ( u₁ ) . Произвольно из заданной области можно взять и любую другую входную переменную. Следующую входную переменную и * ( t ) находим в соответствии со следующим алгоритмом:

s

* u

Е и 2 Ф

I = 1

*

^и 1

-

^{и 1}

где < n >, < р >

–

s

Е ф i=1

V

Г и.

^cu 1

* i

1- ^ 1

V    ^Си .

< n >

п Ф

7 j = 1

< n >

п Ф

7 j = 1

j xj

V j xj

-

j

cY

xj   7

< р >

п Ф

V = 1

—

x j

c

V    xj   7

< р >

п Ф

V = 1

j

M v

V

j

Mv

-

mV '

cv  7

- m V 1

V   cmv   7

размерность соответствующих составных векторов x и м ,

< n > <  n, <  p > <  р . Далее входную переменную и * ( t ) находим следующим образом:

* u

s

Е u зф

i = 1

*

u i

-

и1- ^Ф

*

u 2

-

V ^си 1    7

s

Е Ф i=1

*

u 1

-

ui'

Ф

V

*

u 2

^cu 2

< n >

п Ф

7 j = 1

-

i u 2

V    ^си 1    7

c

V ^и 2

< n >

п Ф

7 j = 1

j xj

V j xj

-

x j

c x j   7

< p >

п Ф

V = 1

-

xj'

c

V    xj   7

< p >

п Ф

V = 1

j

Mv

V

Г *

j

M v

—

mV '

^c m v 7

- m V ¹

c

V Mv 7

.

И далее алгоритм управления продолжается для нахождения каждой компоненты входа u * ( t ) объекта, причем с каждым последующим шагом в формулу добавляются вновь найденные на предыдущем шаге значения входных переменных. Запишем алгоритм управления для многомерной системы, который будет выглядеть следующим образом:

* u_k

s

5     к -1   (

Z u k П Ф i = 1      к = 1     V

*

uk

u k '

^cu k

< n >

П Ф

7 j = 1

x

v

*

i

—

c

x j

x j

5  k— 1   ( zn Ф i=1 к=1    V

*i uk - uk

c

uk 7

< n >

П Ф

* xJ

—

j

< p >

ПФ

V = 1

*

M v

^-

mV )

v

c M v

j = 1 V

c

x j

< p >

ПФ

V = 1

/

J

M*

—

M v

k = 1, m .

V

c

В алгоритме управления (16) настраиваемыми параметрами остаются параметры размытости для входных и выходных переменных c , c и с , для них могут быть использованы следующие формулы:    eUk = Ou * - u*| + П ,    cx = в x* - xil + П    и с и = Дм* — Mi | + П, где а, в и Y некоторые параметры большие 1, а параметр 0 < п < 1. Следует обратить внимание на то, что выбор параметров размытости c , c и с осуществляется на каждом такте управления. При этом если сначала определен c , то определение c и с осуществляется с учетом этого факта. Очередность определения параметров размытости c , c и с несущественна.

Часто в задачах управления реальными процессами число компонент вектора u больше числа компонент вектора x . Если же размерность вектора u превышает размерность вектора x , т. е. m >  n , то обычно поступают следующим образом. В число компонент вектора м включают некоторые (несущественные) компоненты вектора u с тем, чтобы размерность вектора u и x сделать одинаковой.

Вычислительный эксперимент по идентификации. Для проведения вычислительного эксперимента использовался многомерный объект с входными переменными u = ( u , u , u , u₄ ) и выходными переменными x = ( X j, x ₂, x ₃) . Для рассматриваемого объекта была сформирована обучающая выборка входных и выходных переменных, исходя из системы уравнений из двух параметрических и одного непараметрического каналов. В результате была получена обучающая выборка u ₅, x_s , где H_s, x_s - временные векторы. В случае, если бы перед нами находился реальный объект, обучающая выборка была бы получена в результате измерений, осуществляющихся имеющимися средствами контроля.

После получения выборки наблюдений iz_s, x_s можно приступать к исследуемой задаче -нахождению прогнозных значений выходных переменных x по известным входным u . Прогноз для каждой компоненты вектора выходных переменных осуществляется согласно формуле (10).

Настраиваемыми параметрами будут параметры размытости с и c , которые в данном случае возьмем равным 0,4 и 0,3 соответственно (значения были определены в результате многочисленных экспериментов с целью уменьшения квадратичной ошибки между выходом объекта и модели). Объем выборки 5 = 1000, равномерная помеха, действующая на компоненты вектора выходных переменных ^ = 0,07 • По компонентно приведем графики для выходов объекта x , x и x (рис. 3–5).

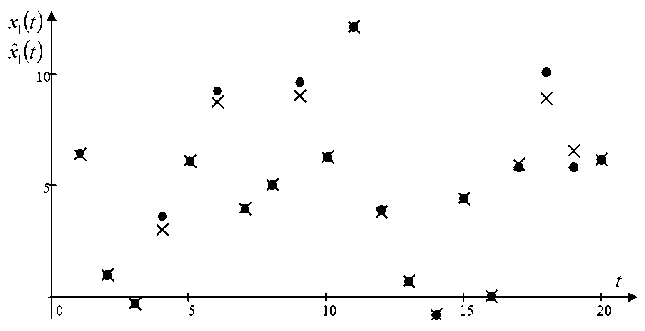
Рис. 3. Прогнозные значения выходной переменной x при помехе 7 %

Fig. 3. The predicted values of the output variable x with an interference of 7 %

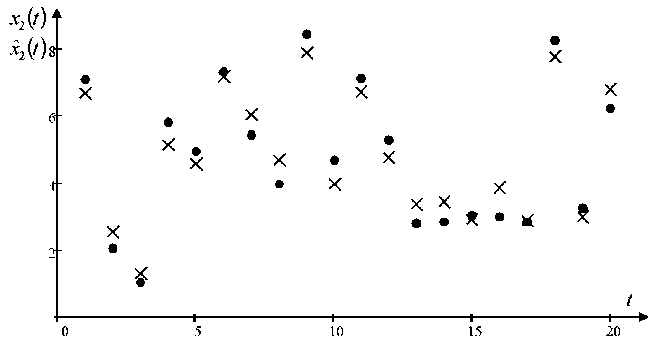
Рис. 4. Прогнозные значения выходной переменной x при помехе 7 %

Fig. 4. The predicted values of the output variable x with an interference of 7 %

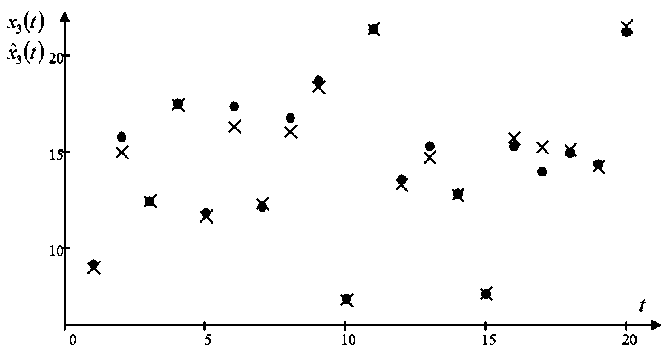
Рис. 5. Прогнозные значения выходной переменной x при помехе 7 %.

Fig. 5. The predicted values of the output variable x with an interference of 7 %

На рис. 3–5 «точкой» обозначены значения выхода объекта, а «крестиком» значения выхода модели, найденные при помощи алгоритма (5), (9). Для наглядности результатов на рисунках представлены 20 точек выборки. Стоит отметить, что модель достаточно хорошо описывает объект при помехе 7 %, действующей на компоненты выходных переменных.

Вычислительный эксперимент по управлению. Приведем результаты вычислительных экспериментов для многомерного объекта с входными переменными u = ( u_x , u ₂, u ₃, u ₄) и выходными переменными x = ( x ,, x ₂, x ₃) при использовании многошагового алгоритма управления (13). Для рассматриваемого объекта можно заметить, что число компонент вектора u больше числа компонент вектора x . Поэтому заменим u ₄( t ) = ^ ( t ) , чтобы размерность вектора u и x сделать одинаковой. Входная неуправляемая, но контролируемая переменная ^ ( t ) е [0, 3].

Еще раз обратим внимание на то, что исследователю неизвестен вид системы уравнений, описывающий управляемый многомерный объект. В качестве информации о рассматриваемом объекте используются измерения входных и выходных переменных ( и , ^ , x , i = 1, 5 ).

Сначала приводятся результаты работы многошагового алгоритма управления (16) при изменяющемся ступенчатом задающем воздействии

x ^* ( t ) (рис. 6).

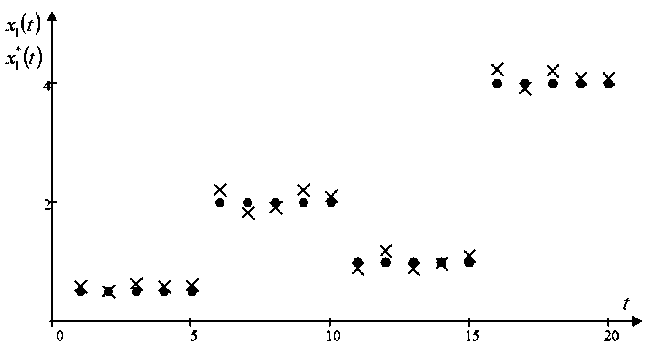
Рис. 6. Управление при задающем воздействии x ² ( t ) в виде ступенчатой функции

Fig. 6. Control under the setting action x ² ( t ) in the form of a step function

Как видно из рис. 6, выход объекта x ( t ) достаточно близок к задающему воздействию X j² ( t ) . Далее приводятся результаты работы алгоритма при плавно изменяющемся задающем воздействии x ^{* ( t} ) (рис. ⁷⁾ .

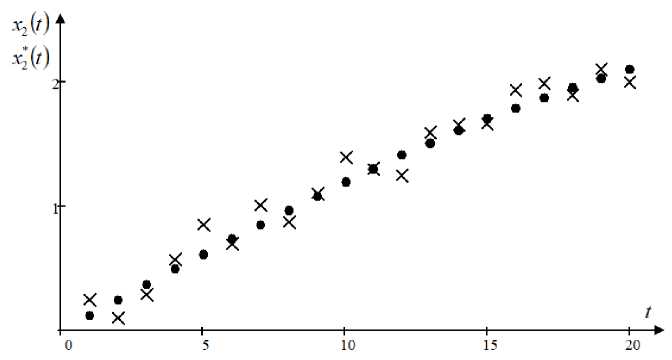
Рис. 7. Управление при задающем воздействии X₂ (t ) в виде плавно изменяющейся функции Fig. 7. Control under the set action X_г (t ) in the form of a smoothly changing function

Далее приводятся результаты работы характер (рис. 8).

алгоритма, когда

задание

x * ( t ) носит случайный

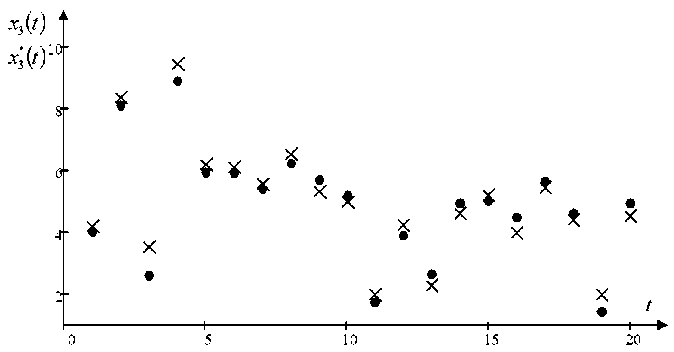
Рис. 8. Зависимость выхода объекта x ₃ ( t ) от задающего воздействия x ₃ ( t ) , носящего случайный характер

Fig. 8. The dependence of the output of the object x₃ ( t ) on the driving influence x ₃ ( t ) ,

which is random in nature

Из рис. 8 можно увидеть, что выход объекта x₃ ( t ) также достаточно близок к задающему воздействию x * ( t ) . С такой задачей, когда задающее воздействие носит случайный характер, не справится ни один из известных регуляторов [14]. Но все-таки такой случай представляет интерес с теоретической точки зрения.

Заключение. В данной работе была рассмотрена задача идентификации и управления многомерными безынерционными системами с запаздыванием в условиях недостатка априорной информации. Здесь можно отметить ряд особенностей, которые состоят в том, что задачи идентификации и управления рассматриваются в условиях непараметрической неопределенности и, как следствие этого, не могут быть представлены с точностью до набора параметров. Хорошо настроенные алгоритмы моделирования и управления могут быть успешно применены в реальных системах управления, диагностики, принятия решений и др. [15].

Приведенные вычислительные эксперименты по идентификации и управлению показали достаточно удовлетворительные результаты моделирования многомерных процессов. При этом исследовались вопросы, связанные с введением различных помех, разных объемов обучающих выборок, но и объектов различных размерностей.