Непараметрический алгоритм управления нелинейными динамическими системами с использованием скользящих режимов

Проблемы, связанные с созданием систем управления динамическими объектами, актуальны по нынешний день в силу сложности математического описания объектов управления и синтеза соответствующих управляющих алгоритмов.

Наиболее развита теория управления линейными стационарными системами. Во-первых, известны подходы к синтезу алгоритмов управления, когда объект управления описывается системой линейных дифференциальных или разностных уравнений [1]. Во-вторых, разработаны алгоритмы управления в случае описания линейной системы в классе обобщенных функций с использованием интеграла Дюамеля или уравнения Винера-Хопфа [2; 3]. В случае недоступности точного описания объекта управления отыскивают его модель, опираясь на априорную информацию о виде и структуре уравнений, законах распределения помех измерений входных и выходных величин и т. д. Принято говорить, что первому и второму вариантам описания объектов в стохастической постановке задачи соответствуют параметрические и непараметрические алгоритмы управления для линейных динамических систем.

Теория управления для нелинейных систем в настоящее время активно развивается. Среди эффективных подходов к разработке алгоритмов управления можно выделить подход с использованием регуляторов со скользящими режимами [4–6], обладающих высокими динамическими показателями и свойством грубости (робастности) по отношению к параметрическим и координатным возмущениям. Управляющее воздействие в методе скользящих режимов синтезируется из условий устойчивости, заданных условиями теоремы устойчивости Ляпунова. Метод имеет следующие особенности:

– применим для нелинейных динамических систем;

– управляющее воздействие отыскивается в классе разрывных функций;

– метод требует знания модели объекта управления (в общем случае модель в пространстве состояний);

– для функционирования регулятора требуется информация о значениях переменных состояния;

– метод устойчив к ошибкам идентификации модели объекта управления и ошибкам измерения переменных состояния.

Постановка задачи. Пусть объект управления задан дифференциальным уравнением, линейным относительно входного воздействия:

x(n) = f (x, x',•••, x(n 1}) + ф( x, x',—, x(n 1)) u , где x = x (t) - траектория движения объекта, его ре акция на входной процесс u =u(t); функции

ф ( x , x ',..., x ⁽ n 1) ) и f ( x , x ',.••, x ⁽ n 1) ) - в общем случае нелинейные и разрывные, потребуем также выполнения условия ф ( x , x ',..., x ⁽ n ^-1) ) * 0.

Определим цель управления как x * = 0 . В ином случае, если x * ^ 0, корректируем функции ф и f так, чтобы цель управления стала x * = 0 .

Вводится понятие поверхности скольжения, изменяющейся со временем поверхности в пространстве состояний, обеспечивающей устойчивость движения системы. Поверхность скольжения задается скалярным уравнением

5 ( x , x ',^, x ⁽ n 1 ) , t ) = 0 .

В общем случае для системы порядка n поверхность скольжения определяется выражением

5 ( x , x ',

n

(n-1) Л I d , I x( ), t = —+ Y

,     I dt    J x, у > 0.

Управление объектом осуществляется в два этапа: вывод процесса на поверхность скольжения и скользящий режим – движение процесса по поверхности скольжения до состояния равновесия. Для обеспечения устойчивости движения к поверхности скольжения вводится функция Ляпунова

V =152.

Условие устойчивости имеет вид

V '< 0, где

V ' = | - 52 I = 55 ' = 5

12 J

d I n - 1 d

—+ Y I —x dt ) dt

= 5 (f + ф u + у);

У = У ( x'^,x ⁽ n °, y ) = ( n - 1 ) Y x ⁽ n ^{- )} + + ( n - 1 )( n - 2 ) y ² x*^{n 2 )} /2! + + y n x '.

Устойчивость движения обеспечивается выбором управляющего воздействия:

где a = const >  0. Решением задачи будет обратная зависимость значений входного процесса от переменных состояния и вспомогательной величины ± a - y :

u = q ( x , x ',., x ^{( n - 1 )} , ± a - y ) .

Для синтеза модели перейдем к конечноразностному представлению:

ud = Qd (x (t), x (t -1)., x (t - n +1), ±a - у (t)).

, 5 >  0,

u < = P, 5 = 0,

>P , 5 <  0,

где

e=-f+y. ф

Метод скользящих режимов доказал свою эффективность для широкого круга практических приложений. Однако, для его использования необходима модель нелинейного объекта управления. Поэтому синтез алгоритма предваряется решением задачи идентификации объекта управления, в частности, в нашем случае, необходимо идентифицировать функции ф и f На практике не всегда возможно отыскать модель в виде уравнения, известного с точностью до вектора параметров, с последующей его оценкой, так как в теории не существует универсального алгоритма идентификации структуры объекта. В работе предлагается отыскивать модель нелинейного объекта управления в классе непараметрических моделей.

Алгоритм решения задачи. Обобщим описание объекта управления:

n)                                (n -1)

x ⁽ ' = ф ( x , x , . , x ⁽ ' , u ) .

Линейность уравнения относительно входного воздействия не требуется. Первая производная функции Ляпунова имеет вид т г f        f ( ( f          (n — 1) \       / f          (n — 1) W

V = 55 = 5 1ф1 x, x ,..., x( ', u ) + У I x ,..., x( ', Yll .

Здесь аргумент t представляет собой дискретную величину: t = 1,2,... Для перехода к дискретной модели используем аппроксимацию производной по времени в виде конечной разности с первым поряд-dx (t) Ax (t) x (t)-x (t-At) ком аппроксимации —— ® —— = ——------- dt      At           At либо с использованием других более сложных схем [7]. Для удобства записи переименуем переменные:

z₁ = x ( t ) , z 2 = x ( t - 1 ) , z 3 = x ( t - 2 ) , ^ , z n - 1 = ^x ( t ^{- n + 1} ) , z n =± a ^- У ( t ) .

В результате получили модель в виде u, = q, (z 1., zn).

Проблема построения модели динамического процесса сводится к решению проблемы идентификации статического объекта, входными воздействиями которого становятся состояния в текущий и предыдущие моменты времени, а также введенная ранее вспомогательная величина.

Во время функционирования объекта накапливаем выборку { z k [ i ] , u [ i ] } , k = 1,2,... n , i = 1,2,... 5 . Полученная выборка используется для построения непараметрической модели Надарая–Ватсона [2; 3]:

us

sn zu [ i ]Пф| zk i=1         k=1 V

sn

ЕПф

i = 1 k = 1

—

zk

[i]

^C sk

zk- zk [ i ]

^C sk

Для устойчивости движения управляющее воздействие u выбираем так, чтобы обеспечивалось выполнение следующих условий:

В случае равенства нулю знаменателя дополняем

модель:

ф ( x , x ‘ , . , x ^{( n —-}, u ) + y ( x ',..., x ^{( n 1 1} , y ) >  0 , если 5 < 0 , ф ( x , x ', x ^{( n — -} , u ) + y ( x' , . , x ^{( n — -} , y ) = 0 , если 5 = 0, ф ( x , x' , . , x ^{( n —-}, u ) + y ( x ',..., x ^{( n 1 1} , y ) <  0 , если 5 >  0 .

u₅ = 0, если

sn еп ф|- i = 1 k = 1 V

^- z k c C sk

[ i ]

= 0.

Параметры C_s удовлетворяют условиям сходимости:

C₅ >  0, lim C₅ = 0, lim 5C₅ =« ,

5 ^ra            5 ^ra

Преобразуем условия устойчивости к следующему виду:

а ядерная функция Ф приобретает вид

n — —

ф(x,x ,., x( ), (f             (n- x,x,.,x(

( f           ( n — 1 )

ф ( x , x , . , x ⁽ ) , u

u ) = a - y ( x ', .		( n - 1 )    \ ., x ( ) , y ) , если	5 < 0,
" ' , u ) =	- У ( x \-	( n - 1 )    \ , x ( ) , y ) , если	5 = 0
u ) = - a	- y ( x V	( n - 1 ) , x ( ) , y ) , если	5 > 0

Перед использованием модели необходимо провести процедуру оптимизации относительно вектора параметров C s = { C s 1 , C s 2 , „., C sn } совместно с параметром а. Предлагается использовать критерий оптимизации, минимизирующий средний квадрат отклонения выходного процесса от желаемого. Критерий оптимизации принимает вид

£ Г x ( u s ( C s , a ) , t )T ^ min.

• t = 0                                          C s ^, a

Указанная форма критерия обусловлена равенством нулю желаемого выхода процесса.

Результаты моделирования. Тестирование алгоритма проводилось на задаче управления положением обратного маятника, совершающего колебания на плоскости, т. е. имеющего одну степень свободы. Требовалось привести маятник в вертикальное положение из некоторого начального состояния, заданного пользователем, а в дальнейшем сохранять это положение. Была взята физическая модель маятника – тонкого невесомого стержня с заданной массой, закрепленной на его верхнем конце. Во время перемещения в пространстве груз испытывает сопротивление окружающей среды. Управляющее воздействие представляло собой момент сил, приложенный к маятнику в точке его опоры – «нижнем шарнире». Движение маятника описывается системой нелинейных дифференциальных уравнений:

a' = to,

• ‘ - g ■       k_Fl 2 ■        . M

to = —sina—— to sign to+—7,

I l m             ml¹

где l – длина маятника; m – масса груза; g – ускорение свободного падения; M – момент сил, действующих на маятник, – управляющее воздействие; k_F – коэффициент сопротивления окружающей среды; a - угол отклонения маятника от вертикального положения; to - угловая скорость маятника.

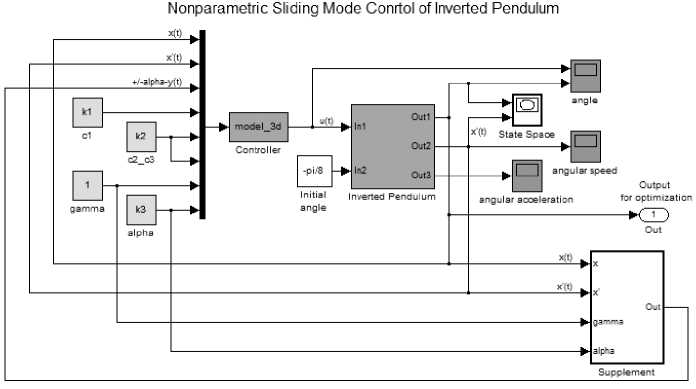
Управляющее устройство включено в цепь обратной связи, оно получает информацию о состоянии объекта управления и генерирует управляющее воздействие. Физическая модель объекта управления устройству управления недоступна. Информация об объекте заключена в выборке измерений переменных состояния и вспомогательной величины, накопленных заранее в процессе функционирования объекта управления. Необходимо отметить, что во время накопления выборки объект управляется с использованием каких-либо других регуляторов, вручную оператором либо, если это допустимо, претерпевает «неудачные» попытки управления в разомкнутой схеме, в том числе, например, реагирует на случайное, хаотическое управляющее воздействие.

Алгоритм управления реализован в пакете MATLAB версии 7 с применением визуальной системы моделирования динамических процессов Simulink (рис. 1).

Блок Inverted Pendulum содержит физическую модель обратного маятника. На вход блока подается значение начального угла отклонения маятника от вертикального положения Initial Angle , а также входное воздействие u ( t ) , которое генерируется управляющим элементом Controller . Входная информация для элемента управления: переменные состояния x ( t ) и x '( t ) , вспомогательная величина ± a - y ( t ) , параметры размытости c 1 , c 2 и c 3 , коэффициенты а и у . Блок Supplement вычисляет значение вспомогательной величины на каждом такте управления.

Как отмечалось ранее, перед использованием алгоритма должна осуществляться процедура оптимизации с применением среднеквадратического критерия. Оптимизация проводилась методом сопряженных градиентов с мультистартом по параметрам, обозначенным на схеме k ₁ , k ₂ и k ₃ . Из практических соображений эти параметры были выбраны следующим образом: к 1 = c 1 , k 2 = c 2 = c 3 , k 3 = a .

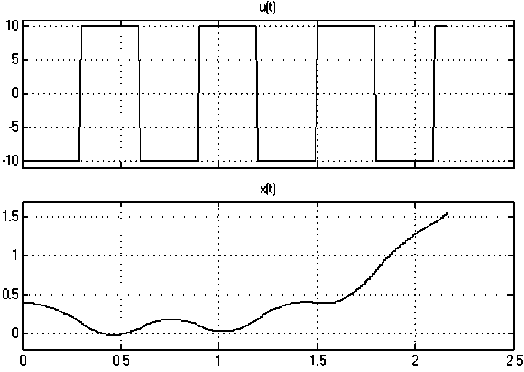
Результаты одного из экспериментов приведены ниже (рис. 2).

Рис. 1. Модель Simulink, реализующая алгоритм управления

Рис. 2. Тестовое управляющее воздействие и реакция маятника в разомкнутой схеме

Момент времени, когда процессы прерываются, соответствует падению маятника на условную горизонтальную плоскость, т. е. x ( t ) = л/2. Объем обучающей выборки 5 = 218, выборочные значения поступают через равный временной интервал A t = 0,01 и не содержат случайных ошибок.

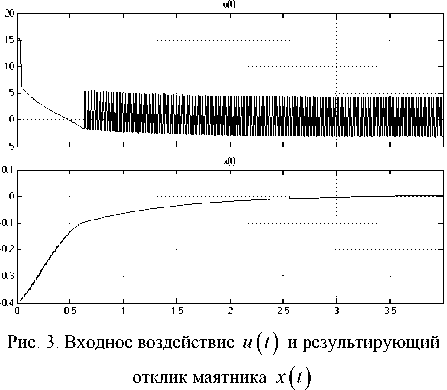
Начальное положение маятника было принято x ( 0 ) = -л/8 «-0,39. Это значение лежит вне диапазона обучающей выборки, в этом нетрудно убедиться, взглянув на рис. 2. Остальные параметры l = 1 м, m = 1 кг, k F = 0, y = 1. В результате оптимизации были вычислены следующие значения параметров устройства управления: с 1 = 0,8 , c ₂ = c ₃ = 1,7, а = 0,7 . Результат управления маятником изображен на рис. 3.

Нетрудно заметить, что входной процесс u ( t ) состоит из двух составляющих: гладкой и осциллирующей. Они соответствуют двум стадиям работы регулятора: выводу на скользящую поверхность и режиму скольжения (рис. 4).

Выход на поверхность скольжения 5 = x ( t ) + x '( t ) = 0 происходит со второй попытки. Осцилляция во время процесса скольжения наблюдается в области значений производной выходного процесса.

Рис. 4. Траектория управляемого движения маятника в пространстве состояний

Таким образом, использование непараметрического подхода к идентификации позволяет осуществить метод скользящих режимов в управлении нелинейным динамическим объектом, модель которого невозможно получить с точностью до набора параметров. Генерация управляющего сигнала в классе разрывных функций позволяет свести к минимуму негативный эффект ошибок (как ошибок идентификации, так и влияния случайных ошибок измерений) в осуществлении процесса управления.

В настоящей работе была предпринята попытка построения эффективного непараметрического алгоритма управления, информация для функционирования которого заключена в обучающей выборке. Выборка должна быть известна заранее, до начала процесса управления. В дальнейшем необходимо совершенствование предложенного алгоритма управления и создание его адаптивной модификации.