Непараметрическое моделирование и управление многосвязными системами

При моделировании и управлении сложными технологическими процессами часто возникает ситуация, когда параметрическая зависимость по ряду каналов объекта не известна полностью или частично. В этой связи для целей моделирования и управления перспективным является использование теории непараметрических обучающихся систем [1]. Рассмотрим формулировку задачи идентификации и управления для одного объекта, который естественно считать фрагментом технологического процесса.

Общая постановка задачи. Приведем схему управления процессом (рис. 1).

Рис. 1

Примем следующие обозначения: О - объект; АС -адаптивная система; и₍ - управляющее воздействие; ц _t - контролируемое неуправляемое воздействие; £ _t - случайное воздействие; х, , z_t - выходные переменные; h ^u , h ^ц , h ^x , N - помехи в каналах измерения; и * , ц h , х ,* , z * - измеренные значения соответствующих переменных; х * и z * - заданные значения выходных переменных.

Следует заметить, что блок АС представляет собой достаточно сложную структуру, детализацию которой в данной статье приводить не будем, лишь укажем, что в ее состав входят как модель исследуемого процесса, так и соответствующая процессу иерархия блоков управления.

Целью системы управления является поддержание заданного значения х , * и z ,* . Отметим существенное значение и отличие выходных переменных х , и z _t : переменная х , контролируется через достаточно малые интервалы времени A t , как и переменные и, ц _t , а переменная z , - через существенно большие интервалы времени A T ( A T » A t ).

С технологической точки зрения, для всего технологического процесса наиболее важным является контроль переменной z. Например, выходная переменная х контролируется с помощью различного рода индукционных, емкостных и других датчиков, аzt измеряется в результате химического анализа, физико-механических испытаний и др. Этим и обусловлено существенное отличие диск ретности контроля выходных переменных х, и z,. Если дискретность измерения х и , ц - это секунды и минуты, то дискретность z, составляет с мену, сутки, недели иболее. Последнее обусловлено технологией проведения самого контроля, который обычно регламентируется государственными стандартами. Приведем сравнительно простую схему технологического процесса (рис. 2).

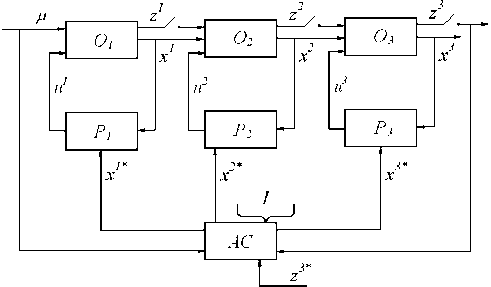
Рис. 2

На этой схеме опущены помехи, действующие в каналах измерения, чтобы не загромождать рисунок. Но предполагается, что они, конечно же, действуют (см. рис. 1). Содержание переменных соответствует описанному выше. Отметим лишь, что роль неуправляемых переменных в этой схеме играют как ц _t , так и z , ', z , ² , контроль которых производится через различные, но значительные интервалы времени. Блоки Р_р Р ₂ и Р ₃ - это регуляторы соответствующих объектов О , , О ₂ и О ₃ , 1- вся имеющаяся информация о процессе.

Математическая постановка задачи. Пусть ^ц t - { ^ц , ,•■■, ц , } ^е R^k , и , - { и * ,..., и ™ } ^е R ^m , х , - { х , *, ..., х " } е R " , z , - { z * , .,z , } е R ¹ . Характеристики объектов О , , О ₂ и О ₃ взаимооднозначны по вектору управляющих переменных, т. е. одному значению и , соответствует только одно значение ц _t . Имеется обучающая выборка { ц _t , и, , х, , z_{t -т} , t = 1, 5 }. Здесь т указывает на запаздывание (смена, сутки и т. д.).

Сформулируем критерий оптимальности:

^R ( z) = M u, ц^{ M z ^{( z} — z )²| u , ц ^} = ^min ,       (1)

,r                                         z где z - оценка вектора выхода z.

Используя необходимое условие минимума, т. е. (приравняв производную функции R по искомой величине z к нулю), получим zopt = M(z | u,ц}.                    (2)

Непараметрическая оценка выходной переменной z для системы, представленной на рис. 1, имеет вид

k zs+1

sm

L z. ПФ i=1       j=1

jj us+1 j - ui    J

n

П Ф

^^^^^^.

M i r ¹

5 = 1, Q ,

(Ю)

sm

LП Ф

jj us+1 j - ui

V

С p ц s

s

Q

n

^^^^^^.

M i r¹

,

” 3 5 z s +т

где s - размер обучающей выборки; z_{s +1}' компоненты вектора выхода, к = 1, l ; и ^ -

p ц I

k

- оценка

к -й

вектор входа

из экзаменующей выборки; Ф -ядро функции, выбира-м ется по следующим условиям: J Ф( b) db = 1, ОО

-“

Ф ( b 1 ) <Ф ( b 2 ) для | b ₂ 1 < | b 1 1 , J b^p Ф ( b ) db <ю , здесь р = 2, 3,..., b - аргумент функции Ф ; C_u - параметр размытости ядра Ф , удовлетворяет следующим условиям: С „ ^ 0 , ^nCu ⁽ n ) ^ ~ ■ П ^м           n ^ ^м

При выполнении перечисленных выше условий оценка z является асимптотически несмещенной, состоятельной, асимптотически нормально распределенной

Параметр размытости С выбирается по условию

х

£ ^,

L z 3 ⁵ П ф

i =1

s

Q

ЕП Ф

u

u

s +1

s +1

—

ui

u 3 s

—

ui

u ³ s

Q

П ф

2k z s+т

—

z

. 2 к 1

F

/

k

П ф

x

2 p

s +1

—

x

2 p

X

Q

V

z 2 s

П ф

2k z s+т

—

z

, 2 к 1

p =1

F

C^p 2 xs

k

П ф

x

2 p

s +1

—

x

2 p

X

,

z ² s

p =1

C p ₂ xs

5 = 1, A ■

Непараметрические оценки выходных переменных х_£

х_£ ³ записываются следующим образом:

15 x s +1

x . + 1 =

s

L

i =1

s

s

Т

L А⁸Пф

i =1

s

Т

ЕП ф

Г

Г

' £ ^,

u

s +1

u

u

^^^^^s

s +1

s +1

- u i

u ¹ s

- u i

u 1 s

5 = 1, Н

u i ^j

u ² s

Н

D

D

,

/

x

s +1

^^^^^s

x

ц к +1

ц ^к +1

X

N

-

ц к

ц ¹ s

-

k

ц к

ц ¹ s

/

П Ф

z

1 p

s +1

,

^^^^^s

z

1 p

X

выполнения минимума критерия s

R = L (Zi - z, (С))2 ^ min,(5)

i=1

где s - размер обучающей выборки

Критерий оптимальности для оценки управляющего воздействия выглядит так:

R(и) = Mц z{Mu(u -u)2 | ц, z} = min,(6)

u отсюда йopt = M (u | ц, z = z*} ■(7)

1П Ф

i =1 J =1

s

Q

л

. 35

x s +1 =

u

s +1

^^^^^e

u i ^j

u ² s

Н

x

1 k

s +1

x ¹ s

^^^^^ш

x

. 1 к 1

p =1

N

C p ₁ zs

x ¹ s

5 = 1, F

,

L х ³⁵П ф

j =1

s

Q

LП Ф

i =1 j =1

u

u

^^^^^e

u i^j

u ³ s

^^^^^e

u i^j

u 3 s

F

/

П ф

x 2 _sk

^^^^^^

x

F

П ф

k

x ² s

x 2 _sk

^^^^^^

x

k

x 2 s

5 = 1, T ■

П Ф

z

1 p

s +1

^^^^^ш

z

1 p

X

,

2 k

p =1

C^p 1 zs

X

Q

/

П Ф

z

2 p

s +1

^^^^^^

z

2 p

C p ₂ zs

Q

П ф

z

2 p

s +1

^^^^^^

z

2 p

,

C ^p 2 zs

Формула оценки, / -го компонента вектора и в момент времени s +1 записывается следующим образом:

Непараметрические оценки выходных переменных х_£

u s^j +1

sl

Luj Пф i=1     f=1

*f z z

k

-

wr1

х_£ ² , х_£ ³ записываются следующим образом:

' £ ^,

s

N

sl

LПФ i =1 f=1

z s +1 ^- z

j = 1, m ■

k

V ^fC 1

p ц s

^ 1 5

-

ц P

,

u

s + 1

L й ^ ⁵ П ф

i = 1

s

N

z

z

s + 1

s + 1

- z i

z ¹ s

- z'

D

П ф

ц ^к + 1

-

ц к

Н

/

П Ф

p = 1

D

ц ^к + 1

-

ц к

Н

x

1 p *

s + 1

-

x

1 p

х

C p ₁ xs

C p

V   ^ц s

Рассмотрим теперь схему (см^ рис 2) Пусть N , Q , Л -

размерностивекторов г^г^г ³, ^ , Q и Л -размерности векторов г_£ \ г_£ ² и г_£ ³ ; Н, F и Т- размерности векторов х_£ ¹ , х_£ ² , х_£ ³ ; Т , Г и g - размерности векторов и_£ ¹ , и_£ ² и и_£ ³ ;

D - размерность вектора ц t .

г _£ ³ и х _£

Запишем модели прогноза выходных значении г_£ ¹ , г _;

£ ^,

х

£ ^,

х

£

i = 1 j = 1

25 u s +1

1 zs

5 = 1, Т

,

s

Q

L u k ⁸П ф

i =1

s

Q

LП Ф

£ ^,

а также модели расчета управляющих воз-

действий u _£ ¹ , u _£ ² , u _£ ³ для объектов O ₁ ,0 ₂ и 0 ₃

s

A

z

z

2 j *

s +1

s +1

-

z 2 _i j

z ² s

-

z ² i^j

z 2 s

5 = 1, Г

F

F

П ф

,

Непараметрические оценки выходных переменных

г.

L u ^{3 8}П ф

z

s +1

-

zi

T

г_£ ² , г ³ будут выглядеть следующим образом:

' £ ’

35 u s +1

i =1

z ³ s

s

A

s

Т

L z 1 ⁸П ф

u

s +1

- u i

D

ц k +1

-

ц к

LП Ф

z

s +1

-

zi

T

25 z s +т

215 z s +т

i =1

u ¹ s

s

25 L z i

i =1

s

k

' 1

ц s

z 3 s

s

Т

LП Ф

Г

u

s +1

Г

1П Ф

u

s +1

i =1 j =1

u

s +1

- u i

_u 1 _s

5 = 1, N

^^^^^е

ui

u 2 s

^^^^^e

u i ^j

u 2 s

/

П Ф

П Ф

D

П ф

,

z s +т

^^^^^ш

z

z 1 s

z s +т

^^^^^ш

z

z 1 s

ц k +1

¹ к 1

, 1 к 1

-

k

ц к

' 1

ц s

/

П Ф

x

1 p

s +1

,

^^^^^ш

x

Р =1

C^p 1 xs

1 p

X

5 = 1, Q ■

П Ф

Р =1

x

1 p

s +1

^^^^^ш

x

1 p

X

,

C^p x 1 s

П Ф

P = 1

x

f ^кк *

x

к

s +1

^ x 2 ^к *

s +1

1 p *

s + 1

-

x

1 p

X

,

/

x

C p ₁ xs

-

x

2 k

X

k

x ² s

-

x

. 2 к 1

k

x 2 s

3 k *

s +1

-

x

k

x ³ s

. 3 к 1

,

П Ф

^ x 3 к *

s +1

-

x

. 3 к ³

,

k

x 3 s

Численные исследования непараметрических моде-

лей. Приведем пример численных исследований непара

метрических моделей прогноза выходных значений объек

тов последовательного процесса, блок-схема которого

представлена на рис 3. Там применяются следующие

обозначения: O ₁ , O ₂ , O _п- объекты; U , W , К-векторы вхо

дов; Z - вектор выхода; К - элемент запаздывания;

X -Л U ) + h 1 ; У -Л X , ^ ) + h 2 ; Z -/( Y , V) + h 3 ; h 1 , h 2 , h 3 -

помехи

На вход первого объекта подается вектор U - { и _х,...,и_п }. Выход первого объекта - вектор А '- { х ₁,..., х _т } поступает на вход объекта О ₂ . Также на вход О ₂ поступает вектор W= { w _р ., w ^ }. Векторы У - { у ^..у } и V- { v _р ., v _g } поступают на вход объекта О ₃ . Выходом третьего объекта является скаляр Z . Ключ К указывает на то, что истинная величина выхода объекта будет известна только через определенный промежуток времени.

Рис. 3

Пусть имеется исходная выборка U. , W . , V . , X. , У . , Z, , i = 1, 5 , содержащая информацию о входах и выходах всех объектов. Известно, что при измерении входных и выходных величин в каналах измерения действуют помехи с нулевым математическим ожиданием и ограниченной дисперсией.

На основании этой выборки требуется построить модель, которая по известному значению входа U первого объекта, а также известным значениям W и V могла давать прогноз выхода всего процесса.

Будем считать, что объекты относятся к классу статических с запаздыванием, а истинные зависимости - к классу непрерывных дифференцируемых функций. Также предположим, что связь выходов объектов с их входами является однозначной.

Дополнительно отметим, что в численных исследованиях для простоты исходная выборка входных-выходных значений взята не из реального процесса, а из процесса, сымитированного при помощи средств программирования.

Численные исследования представлены для следующих размерностей входов и выходов объектов: ^{U- {} и , ^, .^{, и} ₅ ^}; Х= ^{{ х} 1 ^, .^{, х} з ^}; W= ^{{ w} 1 ^, .^{, w} ₄ ^}; ^у-{у _ру 2 ^}; V- { v ₁ , ., v ₃ }; Z -скаляр.

В зависимости от требований реальной задачи возможно построение двух видов модели процесса.

В модели первого вида весь процесс рассматривается как последовательность объектов. Требуется вычислить выходы на каждом из объектов.

Для данной постановки модель процесса имеет вид /У                 /X /X

Z = f ( Y ( X (U ), W ), V ) .           (18)

Запишем формулу оценки выхода первого объекта: sljjsljj

*, + 1 k = Е X ik П ®    ',       / XH ®    ',        , (19)

i=1      j=1 I Cx          I=1 j =1 I Cx где x5+1 k - оценка k-й компоненты вектора выхода, k = 1,3 ; I - 5; s - размер обучающей выборки; U, 1 - вектор входа из экзаменующей выборки.

Для второго объекта модель записывается следующим образом:

shjjshjj

X . n = Е yn П ^ф   _г      / ХП ^ф   _г ,(20)

• i = 1 j = 1    ^ Cy J i = 1 j = 1    ^ Cy ,

^где n — 1,2 ^; X_s +1 ^{ x_s +1 ^,...^, x _s +1 , W_s +1 ^,...^, W_s +1 ^{} ;} e ³, t 4 (размер вектора ^ ); h - e + t .

Для третьего объекта модель строится аналогично: srjjsrjj z...=2лПф      y  /ЕП®      y .(21)

• i =1 j =1 ! Cz J i =1 j =1 ! Cz J

• ^гд^е Y +1 = ^{ y 5 +1 ¹ ,-, y 5 +1 d , v_$ +1 ^{1 ,}...^, V_$ +1 f ^{} ; 7} З+^ркм^р вектора V ); г - 7 +/.

В модели второго вида процесс рассматривается как единый объект Входами являются векторы U , W , V , выходом - вектор Z . Модель для данной постановки выглядит так:

Z = f ( и , W , V ) .               (22)

Компоненты вектора Z находятся по формуле

5 Г (с j_„j А 5 r (a jj А z 5 +1 = Е z i ГТ ®!     , g / ЕГТ ®! ^{+ 1} _Cz ,(23)

^где G 5 +1 = ^{u5 +1 ¹ , -^{, u}5 +1 ⁵ , ^ 5 +1 ¹ , ...^, W 5 +1 ⁴ , V 5 +1 ¹ , ..., V 5 + 1 ^{3 }} ; ^{г - 12}

В исследованиях для всех моделей использовались колоколообразные ядра вида

^ф ( В ) =

0,335 - 0,067( B )²,if( B )² <  5, 0,if( B )² >  5.

Приведем некоторые результаты численных исследований построенных непараметрических моделей.

Пусть истинные зависимости имеют линейный вид:

х ₁ - 1,6 и ₁ + 0,3 и ₃ ; х — ■и ₂ + 0,7 и ₄ ; х ₃ - 0,5 и ₅ ;

у ₁ - 0,5 х ₃ + 0,8 w ₁ + 0,8 w ₃ ; у ₂ — 0,6 х ₁ + 0,8 х ₂ + 0,6 w ₄ + + 0,5 w ₃ ; z - 0,7 у ₁ + 0,6 у ₂ + v ₁ + v ₂ + v ₃ .

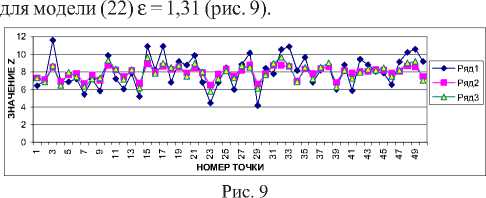
Ниже приведены результаты расчета выхода ^ модели (18) (ряд 2) в сравнении с результатами работы модели (22), (ряд 3) и реальными значениями Z (ряд 1) (рис. 4.9).

Объем обучающей выборки s = 200; U выбирались случайным образом из [0; 5]; ^и К-аналогично из [0; 1]. Экзаменующая выборка s = 50; h - 3 %; среднеквадратичные ошибки прогнозирования модели (18) е - 0,38, модели (22) е - 0,37 (рис. 4).

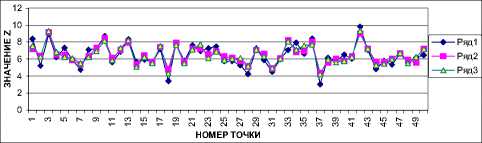
Рис. 4

Часть зависимостей нелинейная.

Пусть истинные зависимости имеют вид х 1 - sin(5 и 1) / (12+и 1) + .6 и 1; х 2= 2+1,3sin(-.2 и 2)+.8 и 3;

х ₃ -2.3sin(0.3 и ₄ )+1.3sin(.3 и ₅ )+.6 и ₁ ; у ₁ - w ₁ ехр(.7 х ₃ ) + 2 w ₂ )/ 5;

у ₂ -.6 х ₁ + 1.5 х ₂ + 1.7 w ₂ + 2.5 w ₄ ; z = .1.3sin(.2 у ₁ )+.7 у ₂ + + 1.5 v ₁ + 1.3 v ₂ + v ₃ .

Объем обучающей выборки s - 200; U выбирались случайным образом из [0;5]; ^и К-аналогично из [0;1] . Экзаменующая выборка s - 50; помехи h _шах - 3 %; среднеквадратичные ошибки прогнозирования для модели (18) е -1,27, для модели (22) е - 1,03 (рис. 5).

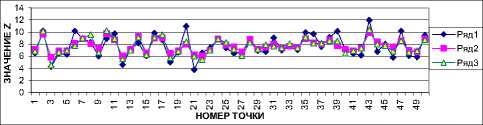
Рис. 5

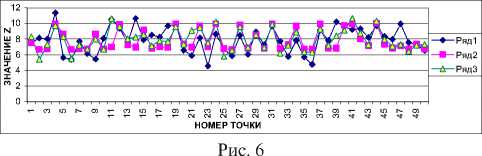
Обучающая выборка содержит всего 20 точек; h^ = 3 %; среднеквадратичные ошибки прогнозирования для модели (18) е = 2,49, для модели (22) е = 1,87 (рис. 6).

Объем обучающей выборки 200 точек; U выбирались из [0;5], ^-из [0;3] и V- из [0;4], h _шах = 3 %; среднеквадратичные ошибки прогнозирования для модели (18) е = 8,50, для модели (22) е = 3,20 (рис. 7).

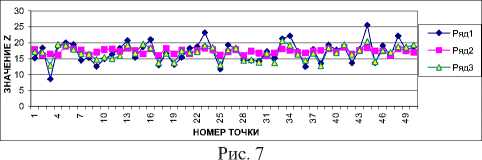
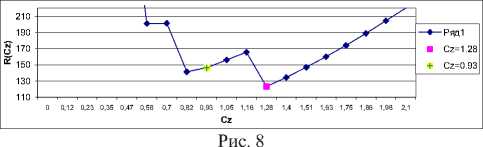
График зависимости квадратичного критерия R от С для модели (18) (рис. 8) показывает, что С =1,28 - это наилучший параметр, определенный с помощью данного критерия ( R (1,28) = 1,27). На самом же деле наилучший параметр лежит левее найденного ( R (0,93) = 1,03). Данный факт объясняется тем, что мы имеем дело со стохастическими данными.

На основании графиков (см. рис. 4.. .9) можно сделать вывод, что модель (22), в которой процесс рассматривается как единый объект, в среднем дает лучший прогноз выхода всего процесса, чем модель (18), в которой процесс рассматривается как последовательность объектов. А если влияние входов ^и Г значительно, то модель (18) работает плохо.

Анализ численных исследований. Для исследований моделировались обучающие выборки малых объемов, при наличии помех и «дыр», что максимально приближено к реальным условиям.

В результате сравнительного анализа, как мы уже отмечали выше, было выяснено, что модель (22) дает более объективный прогноз выхода всего процесса, чем модель (18). Это можно объяснить тем, что во втором случае на вход модели, кроме измеренных величин, подаются оцененные величины. Во-первых, повышается размерность задачи, а во-вторых, поскольку оцененные величины являются не точными, то они искажают конечную оценку.

Кроме того, численные исследования модели последовательного процесса (18) показали, что если влияние неуправляемых входов значительно, то данная модель работает плохо. Причина заключается в выборе параметра размытости, поскольку для модели (18) требуется более сложный механизм настройки параметров размытости, чем для модели (22).

Таким образом, произведенные исследования показали, что непараметрические модели последовательных многомерных процессов дают хорошие прогнозы при обучении на достаточно малых обучающих выборках. Предложенные в статье обучающиеся непараметрические алгоритмы управления могут быть модифицированы и использованы при разработке реальных компьютерных систем управления многосвязными процессами.

Возникает случай, когда в некоторых областях наблюдения отсутствуют обучающие точки, т. е. случай с

«дырами» в обучающей выборке: U _{о6уч е} (0; 1) U (2; 4) U (4,5; 5), W е (0;1) , V е (0; 1) , h _шах = 3 %; среднеквадратичные ошибки прогнозирования для модели (18) е =1,71,